IMC耦合PID的节流阀控制的汽车稳定性研究

张柏军，杜 峰，刘元伟

（1.潍坊科技学院 汽车工程学院，山东 寿光 262700；2.山东科技大学 交通工程学院，山东 青岛 266590；3.中国矿业大学 机电工程学院，江苏 徐州 221008）

1 引言

汽车牵引力控制系统一方面能够提供汽车行驶过程中所需的牵引力，另一方面还具备防止车轮打滑的作用。对此，各国专家学者提出了多种对应的控制算法，例如：基于状态观测的反馈控制[1]、模型预测控制和PID控制等[2-3]，以上算法可以进行不同的组合，形成新的控制算法。文献[4]通过应用单神经元结合前馈控制实现对汽车橫摆力矩控制，把质心偏角控制作为控制目标，建立人车结合的闭环控制系统，并进行仿真实验；文献[5]提出通过自校正控制器来实现前轮的转向控制，此过程需要测试汽车高速行驶下的响应参数，这对系统参数识别精度提出了更高的要求，难以满足，给系统的稳定性带来困难；文献[6]应用软件ADAMS构成汽车的非线性模型，并利用神经网络算法对其进行控制，实验表面：该方法对道路变化和汽车车速变化的应变能力有待商榷，但是在速度均匀变化和道路一定的条件下，能够对汽车的稳定性进行有效的控制；此外，根据文献[7]，鉴于常用乘用车发动机输出扭矩是由内燃机产生的，通过控制器控制发动机扭矩输出量来达到控制牵引力的效果，研究表明驾驶员踩油门踏板并推进到极限的过程，能产生发动机所需的扭矩，从而以发动机扭矩为控制目标，设计相应的控制器，能够对汽车牵引力起到有效的控制，从而提高汽车的稳定性。但是在控制设计过程中，PID控制增益调节较为困难。

针对这一点，提出了一种提高车辆纵向稳定性的设计方案，首先分析内模控制原理和特点，构建车辆动力学模型，确定车辆轮胎和发动机模型，并建立基于模型的牵引力控制系统，通过引入MIC-PID整定方法完成对PID增益的调节，最后通过仿真测试控制系统的性能。

2 内模控制原理与特点

内模控制作为一种新的控制算法，源于预测控制，可认为是对Smith预估器的扩展，具有较强的康干扰性和鲁棒性，且设计简便，内模控制的原理基本结构[8]，如图1所示。其设计思想是通过建立对象模型的内部控制模型，使得内部控制模型与对象实际模型并联，利用设计的控制器，使得控制器与内部控制模型的最小相位的逆逼近。

图1内模控制基本原理Fig.1 The Rationale of IMC

图1 中表达了系统的实际输出、期望输出和外部干扰三者之间的关系。图中：y（s）—系统的输出；G（s）—对象传递函数，yref（s）—期望输出；Gˇ（s）是内部模型传递函数；d（s）—干扰信号，Gc（s）—内模控制器。

3 车辆模型建立

3.1 轮胎模型

为减小轮胎模型对车辆动力学模型精度的影响，这里使用魔术公式对轮胎进行建模[9]，主要是因为魔术公式对实验数据具有较高的拟合精度，即使出现极限值情况下，也能在一定的条件下继续使用，表达式如下

式中：Y（x）—输出量，可以是车辆的纵向力Fx，横向力Fy，也可以表述翻转力矩Mx，滚动力矩My，回正力矩Mz。自变量x可以表示轮胎的纵向滑移（转）率或侧偏角等，系数B、C、D、E与轮胎的外倾角以及垂直载荷有关。

3.2 车身动力学分析

根据牛顿第二定律以及上述设定条件，列出如下车辆运动方程：

式中：Fx（纵向力）和Fy（横向力）—根据轮胎模型计算求得的。ω，vx，vy—车轮角速度，纵向速度以及横向速度。Trol和Td—滚动阻力矩以及驱动轮转矩。另外，Iω，m，r，δ，和 RW—车轮惯性，车辆质量，角速度，转向角以及车轮半径。

3.3 发动机模型的建立

选用双状态发动机模型[10]。包括：进气歧管中的空气质量和发动机转速。利用传输延迟法来实现对于四冲程发动机的离散特性。其中该传输延迟法包括进气延迟及点火延迟两种方法，从而延迟扭矩产生的时间。发动机的原理图，如图2所示。

图2 发动机气缸的原理图Fig.2 The Rationale of Engine Cylinder

依据质量守恒定律，可以列出进气歧管中空气质量的状态方程：

式中：mai—流入歧管气体的质量比率；mao—流出歧管（或流入燃烧室）气体的质量比率。从发动机转动动力学出发，发动机的第二种状态模型如下：

式中：Tind—发动机净扭矩；Tfric—发动机摩擦扭矩；Taero—气动阻力距；Troll—滚动摩擦扭矩；TL—负载扭矩；Ieff—发动机惯性的有效值。

4 控制系统设计

4.1 控制系统分析

在汽车车辆中，在湿滑路面突然加速导致的轮胎打滑会降低汽车的牵引力并降低车辆的稳定性。牵引力控制系统的主要作用是通过维持最优滑移率增加作用于轮胎的摩擦扭矩。滑移率可以 s来表示，即 S=（v-wr）/v×100%，式中：ω—车轮转速；V—车辆速度。S=0—车轮处于纯滚动状态；S=1，表明车子处于纯滑动。当司机直线驾驶时，需要更多地纵向牵引力。然而，在转弯的时候，更多的横向牵引力对于避免车辆侧翻起到至关重要的作用。因此，在过弯的条件下需要一个更低的滑移率；在直线驾驶的过程中，相对高的滑移率对汽车稳定性能起到很大的作用。

4.2 控制结构

设计能够控制车轮打滑的方法，以起到优化纵向牵引力。在该方法中，目标滑移率是作为常量输入到系统中的，而针对四轮驱动车辆的控制方案也进行了相应的仿真模拟。

P-I控制器是基于当前车速以及目标车速来计算节流阀开启角度的设备。

式中：θcontrol—目标节流阀开启角度；θinput—司机命令输入的节流阀开启角度；Vwheel等同于Rω；λ—目标滑移率；Vx—纵向速度。

最终控制器的目标节流阀开启角度输出值是目标节流阀开启角度和司机命令控制的节流阀开启角度两者的最小值。

这样的目的是为了避免节流阀开启角度比司机命令控制开启的角度要大。同时完整的牵引力控制系统结构图，如图3所示。

图3 牵引力控制系统结构Fig.3 System Structure of Traction-Control

4.3 控制器设计

由于PID控制器相比于其他控制器，容易实现且控制效果较好，以PID控制器实现对节流阀角度的控制，但由于PID控制器存在增益调节困难，根据内模控制原理，这里引入MIC-PID控制，通过调节唯一的自定义参数，兼顾系统输出性能和鲁棒性，以达到整定PID增益的效果。

根据图1的内模控制原理，实际控制过程中，内模控制模型与对象存在一定误差，内模控制器无法实现，此时，对内模控制模型进行分解，考虑系统鲁棒性，加入F（s）低通滤波，可得到内模控制器：

传递函数为：

式中：ε—低通滤波可调参数，可通过调节该参数满足系统对鲁棒性的要求；γ—对象模型的阶次。根据所建立的车辆数学模型，通过内模控制实现对PID增益进行整定。取低通滤波F（s）阶次为γ=2，则得到反馈控制器的传递函数为：

式中：K=TK p（2ε+τ），Ti=T，Tf=ε22ε+τ，通过调节 ε 的取值，调节系统的鲁棒性。利用IMC-PID整定得出的PI增益值为：Kp=1.93，Ki=1.22。

5 实验结果与分析

在MATLAB/Simulink仿真软件中建立汽车模型，利用增益值执行牵引力控制系统中的比例积分控制，实现对节流阀角度开启的控制。此外，加入司机对节流阀的控制，保持车轮的最优滑移率；最优滑移率作为系统的输入，且当前车速作为最优滑移率的参考。为测试该控制系统，分别设计了在干沥青道路和积雪道路两种状态车辆进行加速。以上两种道路条件下，对轮胎和路面之间的摩擦系数进行准确评估，且通过定义到轮胎模型的参数中，以便模拟车辆在道路上的加速过程。轮胎模型式（1）中的典型路面条件的魔术公式主要参数，如表1所示。

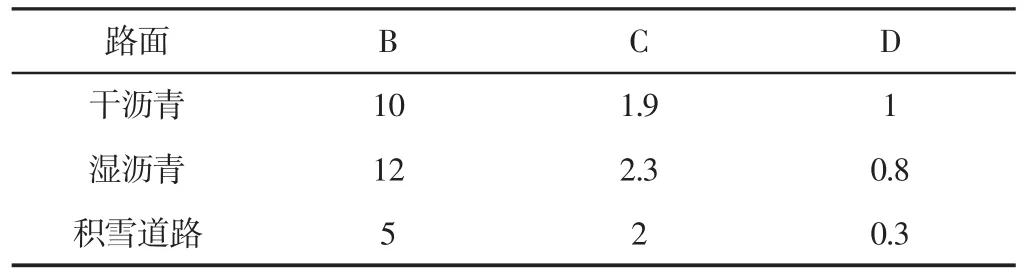
表1 典型路面的魔术公式主要参数Tab.1 Typical Pavement Major Parameters of Magic Formula

在仿真过程中，司机对车辆加速度的指令和控制器仿真指令相同，且假设该车辆模型的最优滑移率为0.06，并且作为控制目标值。

5.1 干沥青道路

在干沥青道路上对车辆加速过程中滑移率控制进行测试。测试过程中，首先分别检测司机和控制器对节流阀开启角度控制信号，如图4所示，图中控制器对节流阀开启角度控制，相对于司机对节流阀开启角度控制总得要大，主要是由于在干沥青道路上，车辆在行驶过程中，车轮与路面打滑较小，滑移率较低，低于最优的滑移率0.06，此时不需要控制器控制节流阀角度达到降低滑移率的目的，致使控制器效果不明显。图5为图4对应的前后车轮的滑移率，很明显，前后车轮的滑移率大大低于最优滑移率，故控制器对节流阀角度的控制未能起到作用，这也符合对牵引系统控制系统的设计要求。

图4 在干沥青路面上，驾驶员和控制器对节流阀的指令图Fig.4 The Throttle Directives of Drivers and Controller on Pavement of Dry Asphalt

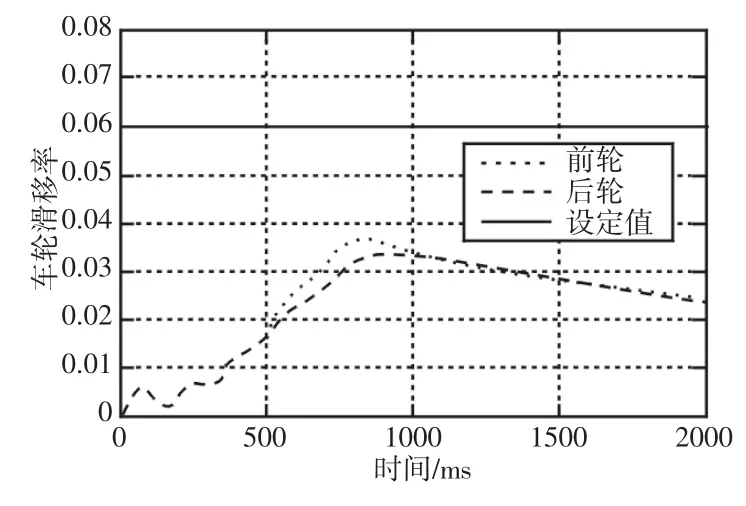
图5 前、后车轮在干沥青道路上的滑移率Fig.5 The Front and the Rear Wheel Slip Ratio on Pavement of Dry Asphalt

5.2 湿沥青道路

湿沥青道路相对干沥青道路易打滑，车辆在行驶过程中，特别是加速过程，打滑的概率相对要高。车辆在湿沥青道路行驶过程中，如图6所示。司机和控制器对节流阀开启角度的控制，图中实线代表的控制器对节流阀角度开启情况，与虚线代表的司机对节流阀角度开启控制相比，控制器控制的节流阀角度在500ms后，要远小于控制器控制指令，此时系统执行控制器对节流阀角度开启指令。控制器减小节流阀开启角度的原因在于车辆在500ms以后，滑移率已经超过最优滑移率，如图7所示。此时，控制器指令通过减少司机指令输出值，使车轮滑移率值控制到最优，从而保证车辆加速行驶过程中的稳定性。

图6 湿沥青的路面条件下，司机和控制器对节流阀的指令图Fig.6 The Throttle Directives of Drivers and Controller on Pavement of Wet Asphalt

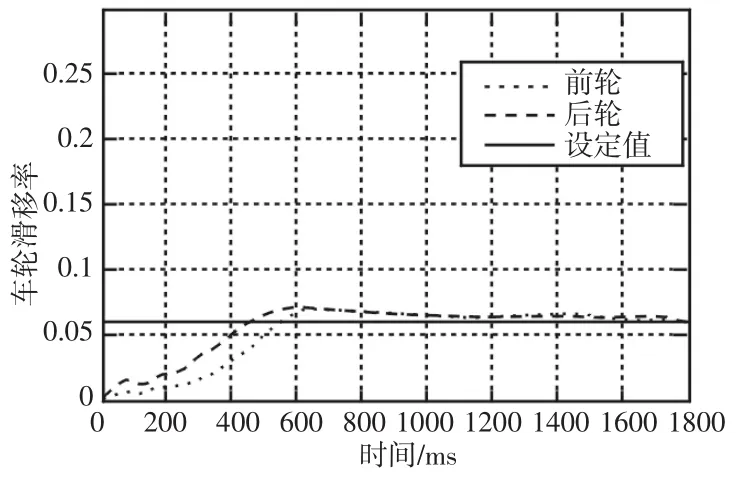
图7 前、后车轮在湿沥青道路上的滑移率Fig.7 The Front and the Rear Wheel Slip Ratio on Pavement of Wet Asphalt

5.3 积雪道路

图8 积雪路面条件下，司机和控制器对节流阀的指令图Fig.8 The Throttle Directives of Drivers and Controller on Pavement of Ice Roads

图9 前、后车轮在积雪道路上的滑移率Fig.9 The Front and the Rear Wheel Slip Ratio on Pavement of Ice Roads

相比与湿沥青道路，积雪道路的打滑更加严重，一般情况下，车辆行驶过程中的滑移率较高，降低滑移率能够有效的保证车辆行驶过程中的稳定性，减小事故的发生。司机和控制器对节流阀的控制指令，如图8所示。在某些点处，控制器的对节流阀开启角度小于司机的控制指令，与湿沥青路面类似，控制器指令试图通过减少司机指令输出值来关闭节流阀，从而使车轮滑移率值控制到最优，如图9所示。

6 结论

通过分析车辆动力学模型，提出了车辆牵引力控制系统设计方案，并利用IMC-PID技术对控制系统中的增益进行整定，实现对发动机节流阀开启角度的控制，确保车辆行驶过程中保持最优的滑移率。通过仿真测试显示：车辆在不使用牵引力控制系统的情况下，车轮滑移率较高，打滑情况十分明显，降低车辆的动态稳定性并导致事故的发生；设计的牵引力控制系统，通过IMCPID技术方法整定的比例积分控制器可以显著降低车辆的最大滑移率并保持车轮在道路上足够的牵引力。