与圆锥曲线准点有关的角平分线性质*

☉湖北师范大学数学与统计学院 孙婉芬 姜 国

圆锥曲线是高中解析几何的重点内容，也是高中数学的难点，为了帮助学生克服这一重难点内容，关于圆锥曲线的研究是很有必要的.许多学者对圆锥曲线的定义、性质展开了广泛的讨论，得出一些有趣结论.如：文2给出了圆锥曲线与准线顶点有关的统一性质.文3证明了过圆锥曲线准线上任意一点的直线平分相关角的性质.文4得到了圆锥曲线焦点与准点的几个有趣性质.文6和文7分别利用代数方程与线性变换的方法证明了双曲线渐近线相关的一个性质.文8利用从特殊到一般的思想，证明了有心圆锥曲线的一个性质.另有部分学者对圆锥曲线相关性质进行了总结归纳，如文1和文5.基于以上研究，本文利用数形结合思想，从代数方程入手，讨论了过焦点直线与圆锥曲线相交的问题，得到几个有关角平分线的重要结论及定理.

结论1：过焦点F的直线交椭圆于A，B两点，Q是焦点F对应的准点，则∠AQB被x轴（或y轴）平分.

特别地，直线垂直于x轴（或y轴）时，由椭圆的对称性，结论显然成立.下面给出直线与x（y）轴不垂直的情形证明：

情形1（焦点在x轴上）：设椭圆的方程为（a>b>0），过焦点F（c，0）（或F（-c，0））的直线y=k（x-c）（或y=k（x+c））交椭圆于A，B两点，点Q（x0，0）是焦点F对应的准点，其中如图1，则∠AQB被x轴平分.

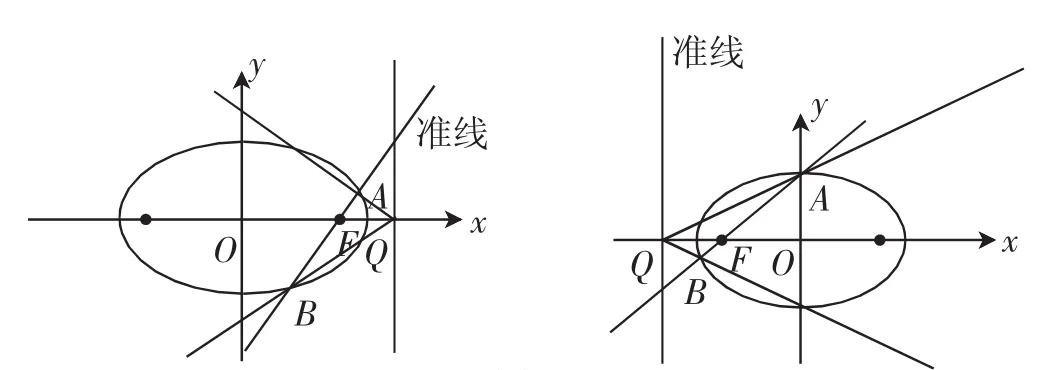
图1

证明：先证过右焦点的直线.

记交点为A（x1，y1），B（x2，y2）.

消去y得（b2+a2k2）x2-2a2k2cx+（a2c2k2-a2b2）=0.

又∠AQF，∠BQF均为锐角，所以∠AQF=∠BQF，得证.

类似可证过左焦点的直线.

情形2（焦点在y轴上）：设椭圆的方程为（a>b>0），过焦点F（0，c）（或F（0，-c））的直线y=kx+c（或y=kx-c）交椭圆于A，B，点Q（0，y0）是焦点F对应的准点，其中则∠AQB被y轴平分.

证明：证明类似情形1，在此从略.

结论2：过焦点F的直线交双曲线同侧一支于A，B两点，Q是焦点F对应的准点，则∠AQB被x轴（或y轴）平分.

特别地，直线垂直于x轴（或y轴）时，由双曲线的对称性，结论显然成立.下面给出直线与x轴（或y轴）不垂直的情形证明：

情形3（焦点在x轴上）：设双曲线的方程为过焦点F（c，0）（或F（-c，0））的直线y=k（x-c）（或y=k（x+c））交双曲线同侧一支于A，B两点，Q（x0，0）是焦点F对应的准点，其中，如图2，则∠AQB被x轴平分.

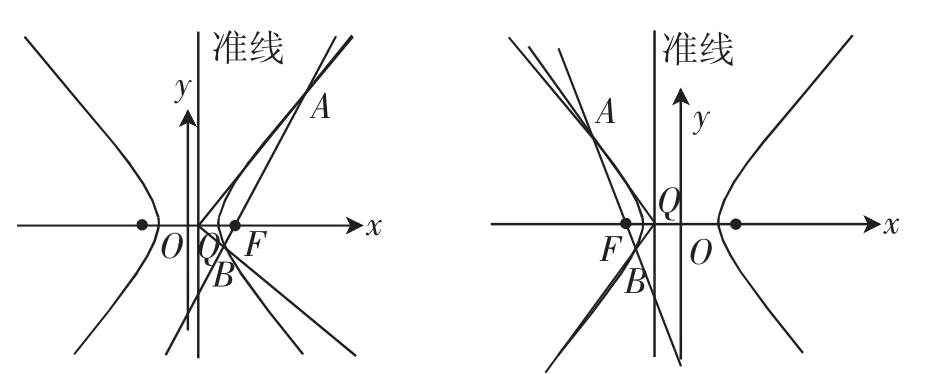
图2

证明：先证过右焦点的直线.

设交点为A（x1，y1），B（x2，y2）.

又∠AQF，∠BQF均为锐角，所以∠AQF=∠BQF，得证.

类似可证过左焦点的直线.

情形4（焦点在y轴上）：设双曲线的方程为1，过焦点F（0，c）（或F（0，-c））的直线y=kx+c（或y=kx-c）交双曲线同侧一支于A，B，点Q（0，y0）是焦点F对应的准点，其中，则∠AQB被y轴平分.

证明：证明类似情形3，在此从略.

注：交点A，B不在同一支时，∠AQB被焦点F对应的准线平分，如图3.

结论3：过焦点F的直线交抛物线于A，B两点，Q是焦点F对应的准点，则∠AQB被x轴（或y轴）平分.

特别地，直线垂直于x轴（或y轴）时，由抛物线的对称性结论显然成立.下面给出直线与x轴（或y轴）不垂直的情形证明：

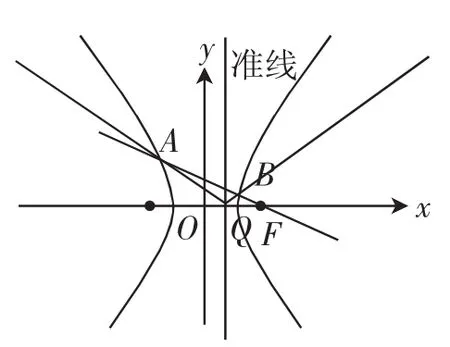
图3

情形5（焦点在x轴上）：设抛物线的方程为y2=2px（或y2=-2px）（p>0），过焦点的直线交抛物线于A，B，点Q（x，0）0是焦点F对应的准点，其中，如图4，则∠AQB被x轴平分.

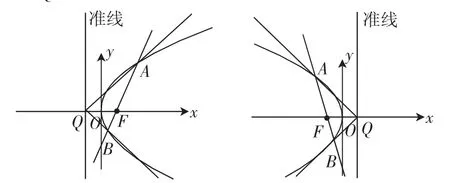
图4

证明：先证过横坐标为正的焦点的直线.

设A（x1，y1），B（x2，y2）.

又∠AQF，∠BQF均为锐角，

所以∠AQF=∠BQF，得证.

类似可证横坐标为负的焦点的直线.

情形6（焦点在y轴上）：设抛物线的方程为x2=2py（或x2=-2py）（p>0），过焦点的直线交抛物线于A，B，点Q（0，y）0是焦点F对应的准点，其中则∠AQB被y轴平分.

证明：证明类似情形5，在此从略.

由上讨论可得如下定理：

定理：过焦点F的直线交圆锥曲线于A，B两点，Q是焦点F对应的准点，则∠AQB被x轴（或y轴）平分.（特别地，对于双曲线，交点A，B位于同一支曲线上）

例1（2018年湖北理科卷）设椭圆的右焦点为F，如图5，过F的直线l与C交于A，B两点，点M的坐标为（2，0）.

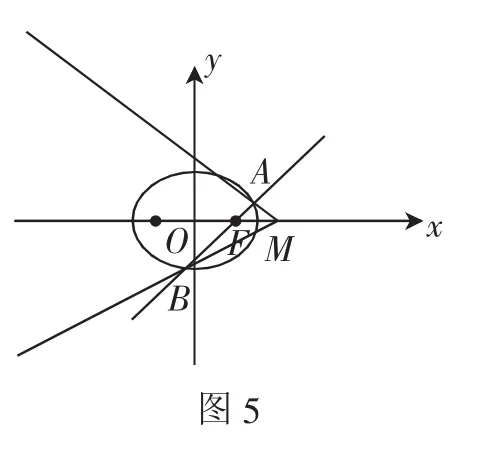
（1）当l与x轴垂直时，求直线AM的方程；

（2）设O为坐标原点，证明：∠OMA=∠OMB.

由结论1知，∠AMB被x轴平分，即∠OMA=∠OMB.