轨道交通车站内通道设施的行人流特性研究

娄永梅 张炳森 张 宁 王 健

(1.北京全路通信信号研究设计院集团有限公司，北京 100070；

2.东南大学智能运输系统研究中心轨道交通研究所，南京 210096；3.南京地铁建设有限责任公司，南京 210024）

1 概述

城市轨道交通作为城市公共交通系统的重要组成部分已成为缓解交通拥堵的重要手段，也因其具有舒适、安全、整洁、准点等优点使得越来越多的居民选择轨道交通出行[1]。

通道是城市轨道交通车站基础设施的重要组成部分，作为连接车站内不同功能设施的缓冲地带，提供了乘客集散和换乘的走行空间，是轨道交通整体性能发挥的关键环节[2]。由于城市轨道交通工程实施难度大、造价高，建成后很难再进行较大规模的改造，因此在设计阶段及建成后运营使用阶段，确保车站设施与乘客的交通需求匹配就显得尤为重要[3]；通道设施的设计必须以行人在通道环境下的行为特征及行人流移动规律为基础，只有通过对行人流交通的深入研究，才能获取通道设施的服务水平与相应通行能力等规划关键技术指标[4]。地铁通道内行人流特性与其他设施内的行人流特性有明显区别[5]，如：1）行人目的性较强，尤其是单向通道内行人的行为呈现出较强一致性；2）间歇性的客流脉冲，由于列车到站的时间间隔，通道内的行人往往呈现出脉冲式的分布规律；3）时间不均衡性，由于乘客出行时间的不均衡，客流一般呈现明显的早晚高峰特性；4）方向不均衡性，车站周边土地性质不同，各个出入口的客流会不均匀，换乘站尤其明显。目前，轨道交通车站内通道的设计大多借鉴国外标准、依赖客流预测以及经验公式等，存在诸多不合理性[6]；另外，近来频发的大客流安全事故，除了一些客观因素外，很大程度上是由于对通道内行人交通特性等基础理论的研究不足导致的。

根据国内外对行人流的研究可以看出，行人流特性具有非常强的“场所-区域”特征，不存在通用的行人流交通模型可适用于所有类型的步行设施。基于以上背景，本文对轨道交通单、双向水平通道内的行人流交通特性进行研究，通过行人流参数实测数据建立相应的关系模型，为车站内行人流线组织、设施布局优化以及设施服务水平（Level Of Service，LOS）评价提供理论指导。

2 数据采集与参数提取

行人交通数据采集是进行行人流统计分析的基础，获取大样本量、高准确度的原始数据对建立可信的行人流交通模型具有决定性意义。行人交通数据采集常用人工观测、摄像记录观测等方法[7]。人工现场观测机动灵活，易于操作，所需的测量工具较为简单，但不易直接测量密度，要观测足够的速度样本，需要消耗大量的人力；摄像记录可提供永久记录、可采取逐帧播放方式统计行人流参数，准确性较高，但参数提取过程比较繁琐。

在从视频录像中获取行人参数时，有2种方法：一是人工统计，二是借助专业的图像识别软件自动获取。但由于图像识别技术对运动中的个体不宜准确判别，易形成较大误差，所以本文采取人工统计的方式从视频录像中提取行人流参数。在行人流数据实际获取过程中，首先进行实地考察，选取固定设施物边界、地面砖体接缝等作为标记，划定考察的区域，并测量划定区域的边界尺寸；然后将摄像机架设在观测区域的上方，采用俯视角度进行观测，方便清晰的观测行人。

2.1 观测对象

本研究以轨道交通车站通道设施为分析对象，根据乘客出行目的不同，通道可以分为出入口通道与换乘通道，根据是否存在对向行人流可以分为单向通道和双向通道，主要起到集散、换乘与引导的作用。为更加明确的了解通道设施内的行人流特性，分别对单向水平通道和双向水平通道内的行人流参数进行采集，选取南京地铁1号线三山街站1号口过道（单向水平通道）和南京站1号口通道（双向水平通道）作为观测对象，如图1所示，两类通道设施的物理参数如表1所示。观测时间为早高峰（07:00-09:00）、 平 峰（13:00-14:00） 和 晚 高 峰（17:00-19:00）。

2.2 行人流参数获取

图1 观测的具体车站Fig.1 The observed stations

表1 通道设施的物理特性Tab.1 Physical features of passageway

在获取行人流数据前应选取合适的统计时间间隔，保证在所选间隔内得到的参数统计结果能够反映真实的交通流特性。统计间隔太短，流量的波动性很大，显得不稳定。统计间隔太长，则密度被“平均”的程度就较大，且考虑车站客流受列车时刻表的影响，选取10 s为时间间隔来统计客流参数。

采用人工统计的方式，从视频录像中采集行人流量、密度和速度等宏观交通流参数指标。当行人流密度较低时，以正常速度播放视频录像进行行人流参数统计；当行人流密度较高时，采用逐帧播放视频甚至反复逐帧播放的方法，确保所获取数据的准确性。下面是各参数统计的方法。

流量：统计10 s内通过通道内观测区域端部横断面的行人数（对于双向通道则是两个方向行人数之和），基于通道宽度可以得到单位宽度单位时间内通过观测断面的行人数，即流量值。

速度：根据速度定义，应统计观测间隔内所有经过通道设施范围的行人速度。即：10 s间隔内所有人通过通道设施范围的距离之和（L）与相应所有人行走时间之和（T）的比值，作为行人流的空间平均速度。但为了减少人工统计的工作量，事先在水平通道内做上距离标记，选取3个有代表性的行人，即在行走过程中不超越他人、也不被他人超越，通过观测样本的走行时间计算得到空间平均速度。

密度：根据密度定义，计算密度应统计10 s间隔内任一瞬间观测区域范围内行人数。考虑到10 s内行人密度的波动以及观测误差，在观测间隔内的前、中、后期随机抽取3个瞬间，统计每个瞬间的行人数，然后取算术平均值作为10 s内任一瞬间的平均行人数；最后，将此平均行人数除以观测区面积得到密度值。

以10 s为间隔，分别统计得到两类通道设施的客流、速度、密度值，通过一定数量的统计，即可得到两类设施行人流参数间的关系。

3 行人流交通特性分析

由于交通环境及个体特性等因素的影响，地铁通道内的行人流会呈现许多不同的宏观现象。关于行人交通流模型的研究方法主要有两种[8]，第一种是基于一定的理论假设，构造某种型式的交通流参数理论模型，继而通过实测数据标定理论模型中的参数；第二种是基于实测数据与统计分析，完全从统计学角度建立参数间的回归模型。由于实际行人设施条件、交通条件差别特大，行人流的随机性又比较强，用理论模型建模难以标定最终参数，所以采取实测数据建立经验模型。

行人流量、密度、速度三者之间的定量关系被称为行人交通流基本模型，其变化规律反映了交通流的宏观运行特性[9]。在速度—密度和流量—密度关系拟合的基础上，行人流三参数只需已知一个，剩下的就可以通过速度—密度和流量—密度方程确定，所以暂不对速度-流量关系进行拟合，只绘制速度-流量散点图并分析变化规律。

3.1 速度-密度关系模型的建立

行人在走行的过程中，直接感受到的状态信息是速度和密度，总是会根据邻近的状况调整自身步行行为，因此从某种意义上说，速度—密度关系是交通流三参数中最重要、最本质的模型，刻画了不同密度条件下个体间相互作用的强度。对采集到的单向与双向水平通道行人流数据进行筛选，剔除异常数据，把个数较少的密度点归到相邻密度点上，绘出速度-密度两者关系的散点如图2所示。

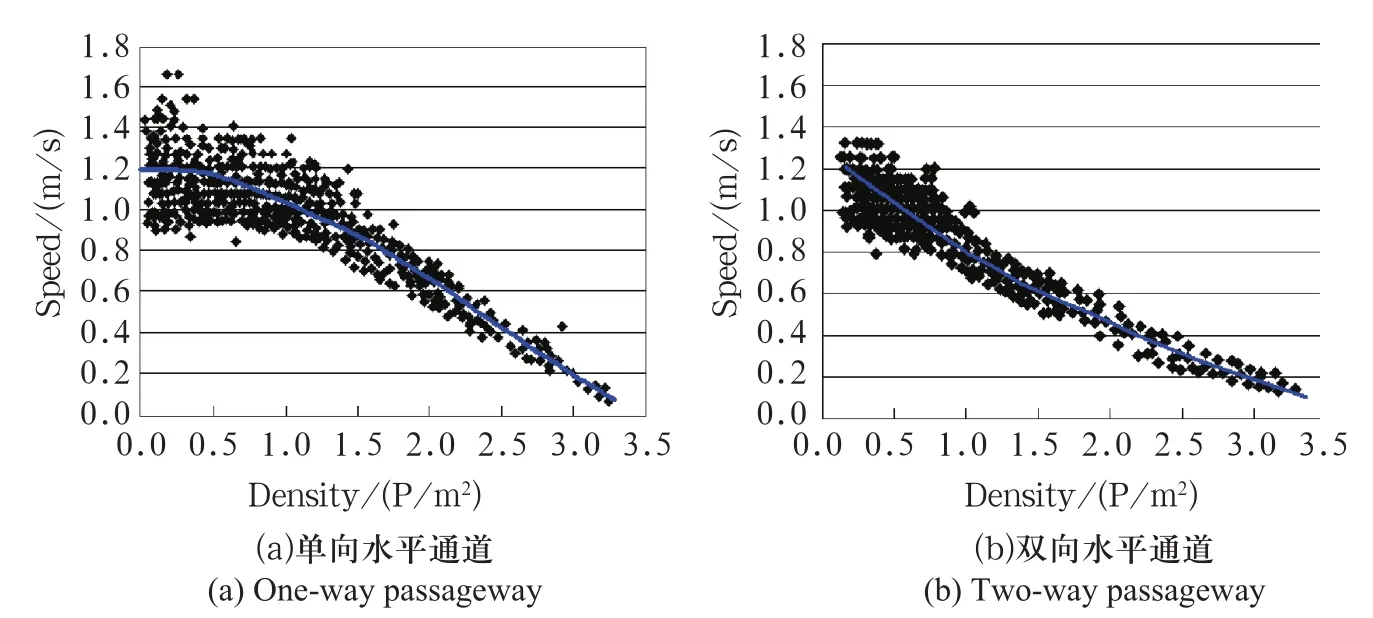
图2 速度-密度关系散点图Fig.2 Speed-density relation scatter plots

对于单向水平通道，当密度小于0.7 p/m2时，乘客近似保持自由流状态的速度，约为0.8～1.6 m/s；双向通道临界自由流密度大约是0.3 p/m2，自由流速度约为0.9～1.3 m/s；在非自由流阶段使用统计软件SPSS对行人流平均速度与密度的关系进行曲线拟合，得出单向水平通道的拟合方程为：V =-0.186 K2+ 0.102 K + 1.224 (K＞0.7),R2= 0.957。双向水平通道的拟合方程为：V = -0.249 K2+0.152 K + 1.312 (K＞0.3),R2=0.964。式中：V表示速度，K表示密度，R2表示相关系数。拟合曲线在图2显示。

可以看出，总体上两种设施行人流的平均速度随密度增加呈现下降的趋势，但并未呈现完全的负相关。在行人密度较低时，速度分布的离散程度较高，随着密度的增加，速度分布越来越趋于集中，直至速度相同。这是由于行人流是由不同运动能力、行为特征的个体所组成，低密度时，快速、慢速行人都可以达到其期望速度，此时行人以不同速度前进；高密度时，由于绕越、穿插机会减少，快速行人不能达到期望速度，其行进速度与慢速行人趋同，行人流以相对一致的速度前进。

比较两者自由流速度和临界密度可知，两类设施的自由流速度基本相同，但单向水平通道的临界密度高于双向水平通道。这主要与两种设施行人交通行为特征有关：单向水平通道行人行为主要有跟随与绕越，双向通道除了同向的跟随与绕越外，还包括对向的避让与穿越。根据个体行走效用最大化原则，双向通道中的行人要减少冲突，最好的方法是跟随同向行人，这也是双向通道出现自组织行为的原因，自组织使得双向通道趋近于两个单向通道的叠加，低密度时自由流速度几乎相同。但由于对向流冲突的存在，双向通道临界密度小于单向通道，行人速度的减小也显著。

3.2 流量-密度关系模型的建立

流量-密度关系模型反映的是不同人流密度下单位宽度设施在单位时间内的行人通过量，主要用于通道设施通行能力与服务水平分级研究[10]。基于单向、双向通道内的实测数据，绘制流量—密度关系散点如图3所示。

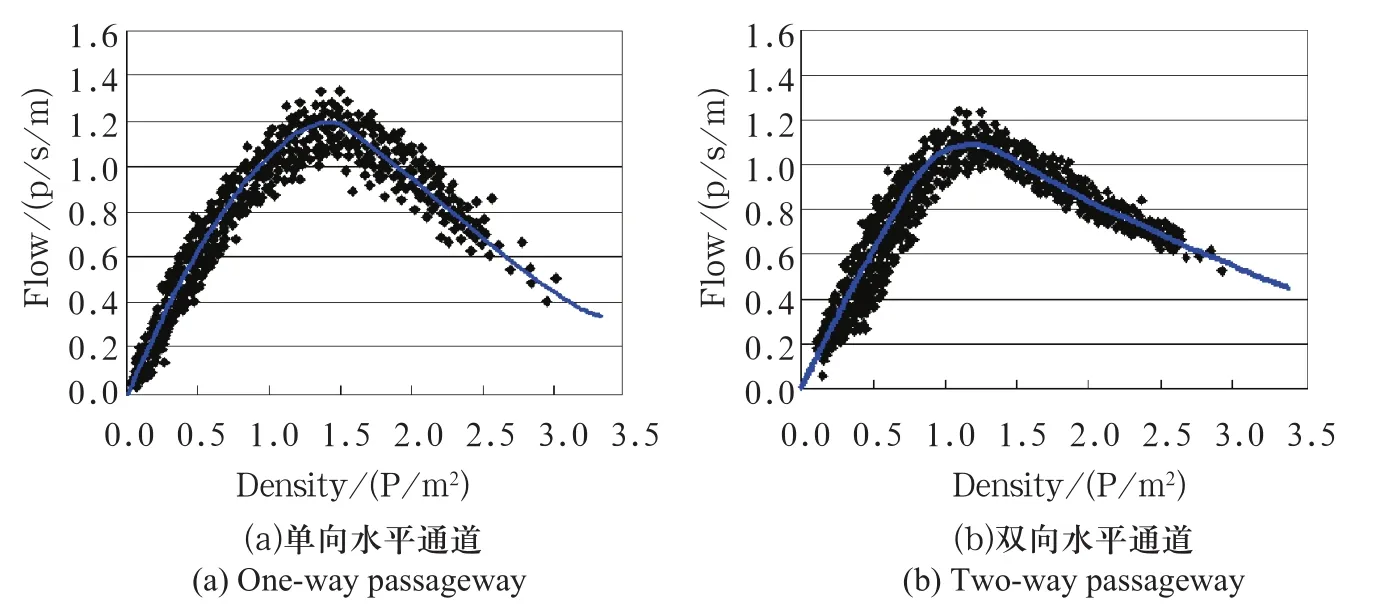
图3 流量-密度关系散点Fig.3 Flow-density relation scatter plots

根据单向、双向水平通道行人流量—密度的散点图，分别用多项式、指数、对数等模型回归流量-密度曲线，选取赤池信息量准则（Akaike’s Information Criterion, AIC）作为评价准则，AIC的值越小，表明模型最优，结果显示多项式模型拟合效果最好，得到单向水平通道流量—密度关系为：Q = 1.440 K - 0.446 K2，R2= 0.990，双向水平通道流量-密度关系为：Q = 1.085 K - 0.038 K2，R2= 0.983。式中：Q表示流量，K表示密度，R2表示相关系数。拟合曲线在图3显示。

对于单向通道而言，流量随着密度的增加而逐渐上升，当到达临界密度1.5 p/m2时，流量达到最大，之后随着密度的增加呈现下降的趋势。在所观测的密度范围内，双向水平通道的流量—密度关系的变化特性与单向水平通道几乎无差别，进一步证实双向水平通道在自组织条件下，趋近于两个单向水平通道的叠加。双向水平通道的流量—密度关系散点图较单向水平通道离散，是由于双向水平通道行人流即存在单向的跟随超越行为，又存在对向的冲突避让行为，导致同等密度下流量变化较单向水平通道离散。另外，随着密度增加，双向人流会呈现自组织现象，形成两个单向行人流，每个单向行人流内部只存在单向跟随与超越行为，但两个单向行人流之间的“接触区域”存在双向冲突避让，因此高密度时，双向通道的流量将比单向通道的流量有所折减。

3.3 流量-速度关系分析

流量-速度关系模型反映不同流量条件下行人流可获得的平均行走能力，由于流量是一种固定断面的度量，因而在本质上行人对流量并不敏感。本文在拟合速度-密度和流量-密度关系的基础上，仅对单、双向水平通道设施的速度-流量的散点图做定性讨论。单、双向水平通道的流量-速度散点如图4所示。

由单向水平通道的散点图可以看出，随着流量的增加，速度总体上保持下降趋势，但在自由流阶段变化并不显著，当流量到达某一阶段时，速度变的极不稳定。双向水平通道的速度随着流量的增加平缓下降。

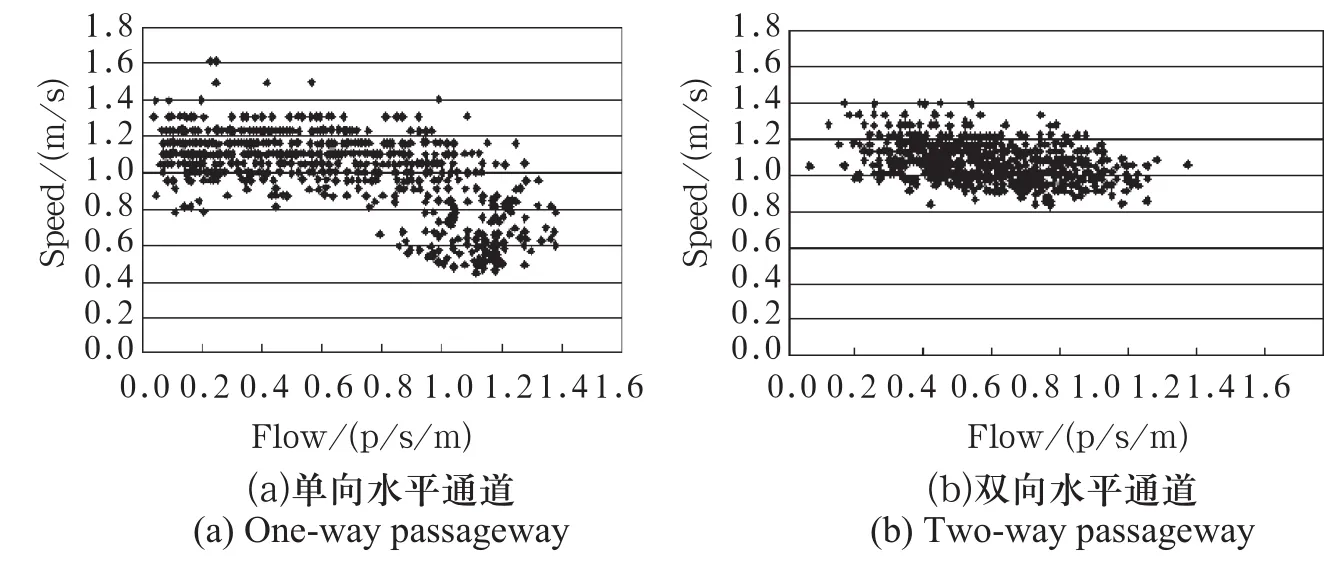
图4 流量-速度关系散点图Fig.4 Flow-speed relation scatter plots

反映“流-密-速”定量关系的交通流模型是分析通道设施交通运行状态的技术基础。对通道设施不同模式（单向、双向）下的行人流关系模型进行分析，区分了单双向通道中行人流特性的差异，为车站内行人流线组织和设施布局优化提供理论指导。同一模式下的行人流关系模型，明确的刻画出交通流的运行状态，清晰反映服务质量的变化与差异，研究结果可以为步行设施规划设计提供指导意义，同时为服务水平的分级提供了明确的标准。

4 总结

轨道交通车站通道设施的设置与乘客密切相关，对乘客流的交通特性研究是轨道交通建设的基础。不同型式、不同区域走行设施的行人流特性是不同的。本文对轨道交通单向和双向水平通道中行人流特性进行研究对比，可以看出，双向通道在人流自组织条件下，趋近于两个单向通道的叠加；单、双向水平通道的自由流速度基本无差别；由于冲突的存在，双向水平通道的通行能力小于单向水平通道，但自组织行为的现象使得差异并不明显；随着客流密度的增大，双向水平通道的行人流速度下降比单向水平通道明显。实际行人流通常由不同年龄、不同性别、是否携带行李、是否结伴行走等按照各不同比例混合组成，在本文的基础上可进一步分析年龄、性别等个体特征要素对轨道交通通道设施的行人最大通过量的影响，进而为通道通行能力的修正及相应的规划设计提供参考依据。