加速遗传算法在小流域水土保持多目标综合优化模型中的应用研究

孙 飞

(朝阳县水土保持局，辽宁 朝阳 122000)

多目标规划法、线性规划法、计算机辅助法、经验以及目的规划法等是目前应用于小流域水土保持综合治理的主要方法，其中多目标规划法不仅解决了线性规划目标单一的缺陷，而且改变了经验和目的规划法中每个规划目标均有收敛性能的现状，因此该方法从数学角度可有效解决小流域水土保持多目标综合优化中出现的问题，在水土保持工程方案中得到广泛的应用和推广[1]。采用SETM法进行多参数的寻优逐步计算是应用于多目标综合规划的常用方法，其基本过程是利用了试算和迭代计算的基本理论，并对SETM法可产生的参数局部最优和早期收敛等弊端进行有效的解决[2]。基于以上问题并预防模型计算进入早期收敛而造成局部最优等问题，将多目标规划理论与加速遗传算法原理相结合的模型理论已成为目前流域多目标综合优化算法的主要方向和研究热点，研究表明该方法具有收敛性能好、全局寻优能力强等优点[3]。文章利用加速遗传算法并结合多目标规划理论构建了水土保持综合优化模型，并以朝阳县六家子小流域为例利用模型进行多目标综合优化研究分析。

1 实数编码的计算遗传算法RAGA

遗传算法是由Holland教授提出的一种对全局择优的概率搜索法，它是基于自然环境中生物的进化和遗传过程等对多目标进行模拟的分析，其基本流程和计算步骤主要包括选择、交叉和变异等。文章对标准遗传算法参数的寻优过程及基本步骤进行了详细的分析和介绍。

步骤一：设定全局最优目标参数f(X)Max;aj≤xj≤bj并求解。结合参数变量的取值范围随机生成具有N组的均匀分布随机变量，对目标函数值进行大小排列。

步骤二：采用eval(v)表征序列参数的评价函数，生成新的物种群落，且对上述计算过程进行交叉计算。根据交叉计算结果对新生物种进行变异计算和迭代计算，上述计算流程和步骤构成了标准遗传算法即SGA法。利用SGA标准遗传法并不能够对全局进行收敛和寻优，往往会在偏离全局最优的计算点达到收敛并停止寻优计算。

步骤三：根据上述SGA的寻优特点和计算过程，对模型运行初期的迭代计算结果中的优秀个体变化范围重新设定为变量的变化区间并进行初始状态计算，重新进行SGA的参数寻优计算。

步骤四：模型对优秀个体的变化区间进行反复的迭代计算可逐步地将其变化区间缩减，计算达到加速运行且离最优点的距离会逐渐减小。

步骤五：模型计算运行直至寻优标准函数值小于预期设定的某一特征值或计算运行次数达到预期的设定，模型运行计算结束。

步骤六：群体中最优的个体即为RAGA全局寻优计算结果，在SGA计算初始时期增加的变化区间重新迭代计算的步骤即构成了加速遗传算法RAGA的形成。

2 基于RAGA的六家子小流域综合优化模型

六家子小流域地处辽宁省朝阳县西营子乡低山丘陵区，流域总面积3720.32hm2，其中水土流失面积1691.01hm2，计划治理面积1224.53hm2，土壤侵蚀模数为3360t/km2·a。属于大陆性季风气候，年平均径流深度112mm，降雨量约510mm，在不同时间尺度的降雨量明显不均匀，每年的7—9月为降雨集中期或汛期。该流域属于土石质中度侵蚀区，土壤侵蚀强烈，并以水力侵蚀为主，流域内水土流失危害严重，对区域农业生产发展和生态环境良性循环构成严重威胁，不利于当地经济和社会的持续健康发展，调查显示每年约0.2～0.8hm2的耕地田坡被水力和风力改造成侵蚀沟。据此，采取有效的水土保持治理措施对保证该区域的经济发展和农业生产具有重要意义，利用科学合理的技术手段对水土保持多目标综合优化体系进行研究可明显降低水土流失带来的危害，促进该区域的水土治理工程的发展和体系制度的完善[4-7]。

2.1 目标函数的选择及处理

文章在充分考虑了朝阳县六家子小流域的自然经济发展规律和水土保持治理现状的基础之上，通过借阅资料并结合以往相关专家的经验确立了该小流域的3个规划体系目标即经济纯收入最大目标、粮食产量最大目标以及土壤流失最小目标，各目标的计算公式分别如下所示：

f1(X)Max=135x1+82x2+60x3+471x4+377x5+250x6+462x7+351x8+280x9+165x10+142x11+

630x12+618x13+347x16+355x17+346x18+842x25+16x26+21x27+75x28+220x29+185x30

(1)

f2(X)Max=355x1+270x2+250x3+1120x4+940x5+780x6+510x7+450x8+260x9+220x10+170x11

(2)

f3(X)Min=0.342(x1+x4+x7)+0.0128x2+0.031(x3+x5)+0.1325x6+0.160x8+0.138x9+

0.076(x10+x12)+0.166(x11+x13)+0.27(x16+x17+x18+x19+x20+x21+x22+x23+x24)

(3)

式中，f1(X)Max—经济纯收入最大目标；f2(X)Max—粮食产量最大目标；f3(X)Min—土壤流失最小目标。

根据遗传算法多目标综合优化基本原理，通过将上述三个规划目标按照线性加权法进行求和，统一规划为单一目标进行求解，其计算公式如下所示：

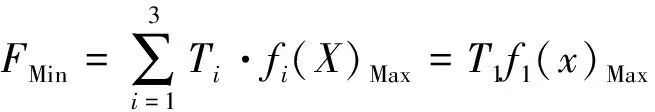
(4)

文章结合相关专家经验，将经济纯收入最大目标、粮食产量最大目标以及土壤流失最小目标分别进行重要性排列，其重要性系数分别为α1为0.6，α2为0.2，α3为0.2。

2.2 确定决策变量和约束条件

研究结合朝阳县六家子小流域土地利用类型及相关适宜性评价标准[8]，在考虑了水土保持实际状况的基础上对综合优化影响最大的参数变量进行设定，而对影响较小的变量进行忽略，最终确定了该小流域的30个决策变量，相关决策变量的统计结果见表1。

多目标综合优化主要考虑了研究流域的土地资源量、净劳动力输入状况、土壤肥沃力、粮食产量、畜牧业发展、人口数量、居民生活需要，可以将上述决策变量划分为4种约束条件即土地约束条件、生产力发展约束条件、平衡约束条件以及畜牧业发展约束条件。

土地约束变量根据其所处的重要等级标准可以分为四个等级的约束：决策变量所受到的一级约束条件为X1+X4+X7=7186.27；二级约束为条件X2+X5+X8+X10+X12+X14+X16+X19+X22=5582.36；三级约束条件为X3+X6+X9+X11+X13+X15+X17+X20+X23=4825.33；四级约束条件为X18+X21+X24=316.77。

生产约束变量应结合当地粮食生产发展力，为满足居民生活需求，良田人均面积不低于0.337hm2，结合小流域当地居民数量有：

X1+X2+X3+X4+X5+X6+X7+X8+X9+X10+X11≥1280

为满足生态要求其人工草场不小于160hm2，则有X14+X15≥1500；林地覆盖率应不低于20%，则有X16+X17+X18+X19+X20+X21+X22+X23+X24≥2551.8；粮食中小麦产量应保持在960000kg，则有420X1+350X2+260X3≥950000；大豆不低于350000kg，则有400X7+320X8+250X9≥350000；杂粮以及经济林等相关目标约束条件文中不一一展开介绍。

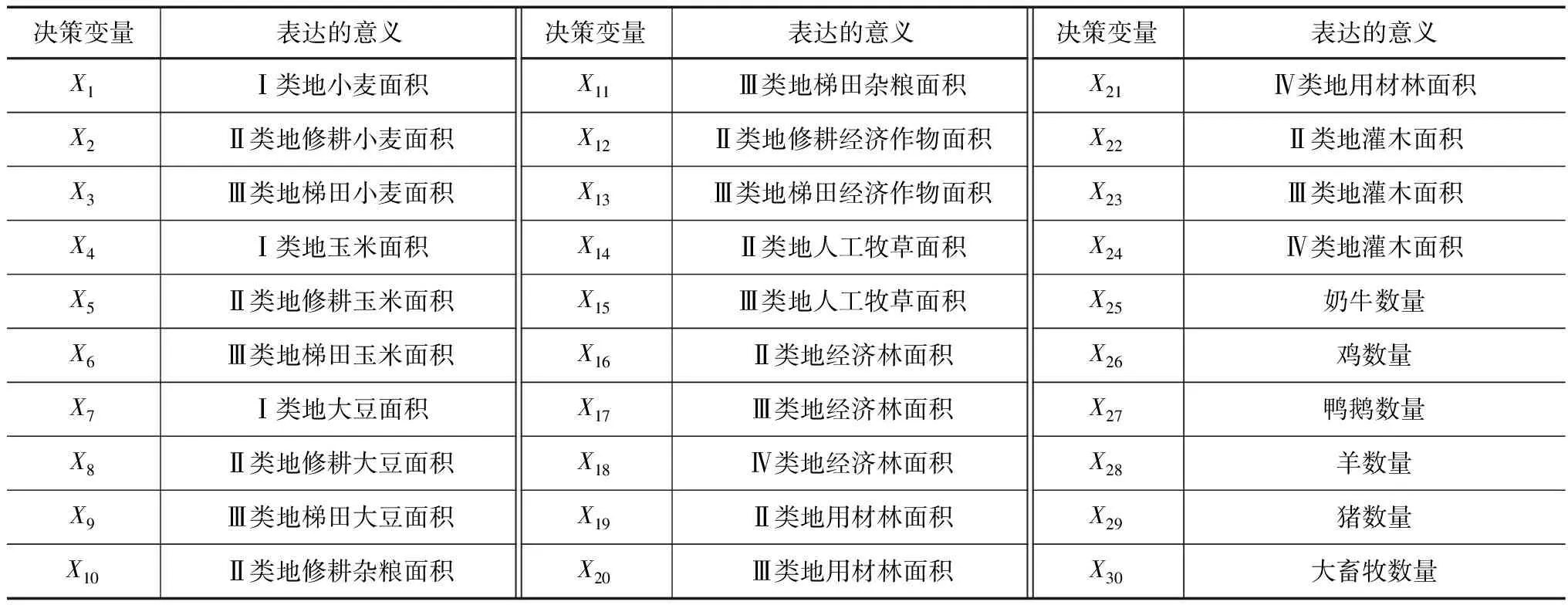
表1 六家子小流域决策变量统计表

对于平衡约束条件主要有畜牧草料平衡约束、有机化肥平衡约束以及粮食平衡约束，其计算公式分别如下所示。

畜牧草料平衡约束条件为：

160X1+125X2+120X3+255X4+220X5+170X6+190X7+130X8+110X9+

120X10+115X11+3100X14+X3100X15-5000X25-1100X28-1400X29-4600X30≥98000

有机化肥平衡约束为：

2500(X1+X2)+1600(X4+X5+X10+X11+X12+X13)+2200X3+1600X6+

1200(X7+X8+X9)+60(X16+X17+X18)-23000X25-500X26-800X27-1700X28-

18000X29-24600X30≤8461000

粮食平衡约束为：

350X1+360X2+270X3+1600X4+1200X5+700X6+420X7+360X8+240X9+230X10+

180X11-13000X25-80X26-70X27-60X28-600X29-680X30≥31557000

对于畜牧业的约束条件有羊：X28=570；猪：X29≤1560；大畜牧数量：X30=540；奶牛数量：X25≥280；鸡数量：X26≤2720；鸭鹅数量：X27≤1550；其他各项均大于等于0。

2.3 约束方程的处理

模型综合寻优受约束条件较多，在计算求解过程中因单位和量纲存在一定的差异，故需对约束条件进行预处理以满足模型的全面约束条件计算[9]。惩罚函数法是在约束条件处理的常用条件，其基本原理是对目标函数定义一个惩罚项以此对变量是否处于约束集内进行计算，并形成一个广义的约束函数，在计算过程中利用惩罚项达到不同受约参数的最优计算，其计算过程可用下式进行表示：

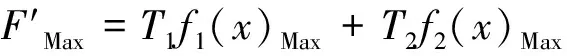
(5)

式中，higi(x)—惩罚项，该值为0时表示约束满足条件，该值为其他实数时表示约束与条件之间的离散程度；F′—优化准则函数。

2.4 遗传算法参数寻优

文章利用MATLAB5.3程序对基于加速遗传算法的30个参数变量同时进行寻优计算，在设定模型初始计算种群个体n为600的同时，假设Pc交叉概率为0.84，Pm变异概率为0.80，确定了20个最终的优秀个体，α取值为0.05，模型的加速次数选取为30次。通过对全局的寻优计算，各目标函数值的最优计算结果见表2。

根据上述表中的参数寻优结果按照不同寻优方案分别进行经济纯收入最大目标、粮食产量最大目标、土壤流失最小目标以及综合优化目标计算，计算结果分别如下所示：

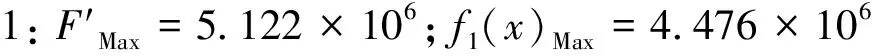
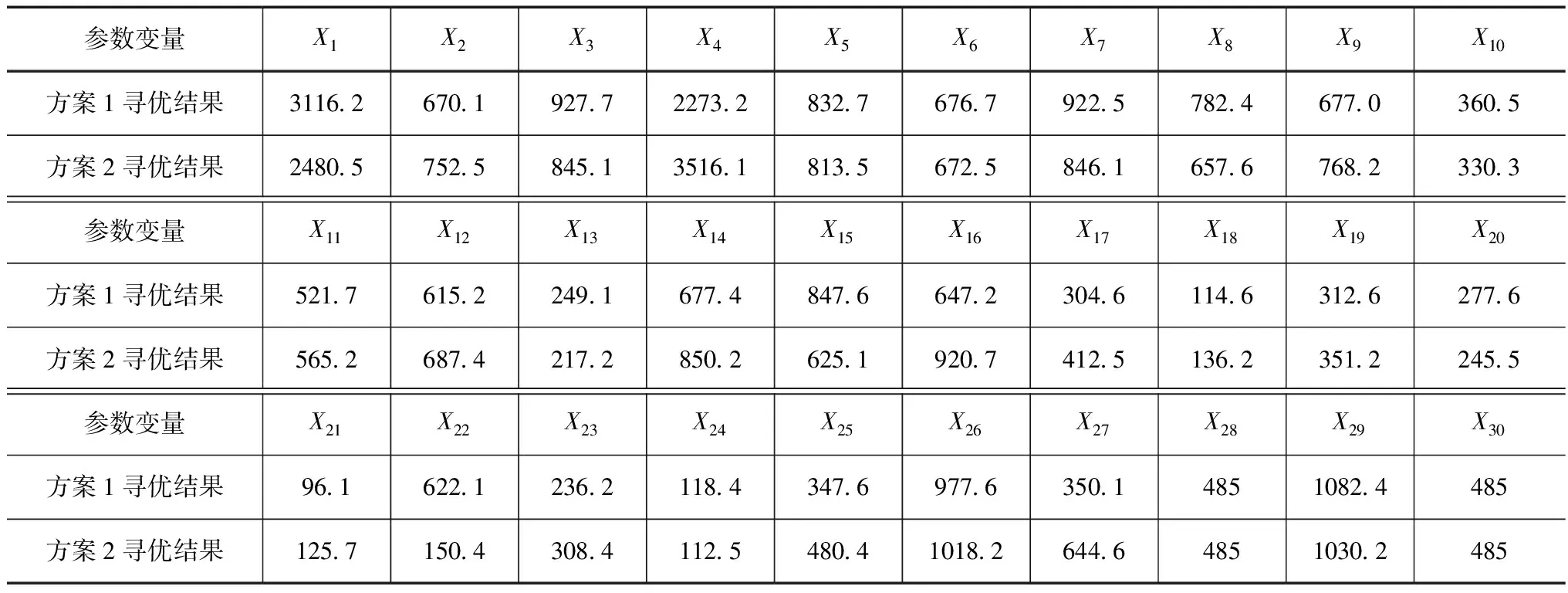
表2 基于加速遗传算法的参数寻优计算结果

2.5 多目标综合优化结果分析

多目标综合优化模型在多个约束条件下利用RAGA法得到的经济纯收入最优解为4215000元、粮食产量最优解为6875500kg、土壤流失最优解为30488t。研究表明，在满足文中所述的约束条件下使得农业土地利用更加合理，采取修砌梯田、结合地形结构改为横坡垄耕作等关键性技术措施将有利于提高土壤有机物含量增加土壤肥沃力[10]。农业用地由77.31%降低为66.25%，林地覆盖率由5.71%增加至16.22%，覆盖面积明显增大。不仅有利于水土保持的工程建设，而且可明显改善生态环境[11]。所构造的经济林和灌木林，不仅经济合理而且可进一步减少水土流失，使得林地覆盖系统功能更加齐全，且利于促进土地资源的合理开发利用；农牧业由0.80%增加值14%，草场质量得到明显改变；居民收入由原来的1282元提高至4660元，提高了将近3.5倍。粮食由原来的人均1182.5kg上升至3844.7kg；水土流失面积明显降低，因水力冲刷侵蚀造成的危害明显减少，林地覆盖率的提高使得生态系统更加合理，且因洪涝灾害导致经济损失显著减少，在约束条件下的土地利用类型分配状况见表3。

根据上述计算结果可知，将约束条件稍微进行改变，则六家子小流域的总体经济效果可获得更大利益。如降低对小麦的产量要求，增加对大豆和玉米等经济作物的耕种面积，则居民经济纯收入以及粮食总产量均有显著的提高，流域内的整体经济效果会更好，公式为380X1+320X2+240X3≥1600000，且方案2的综合经济效益优于方案1，可通过适当调整方案中的约束条件获得更大的经济收益。

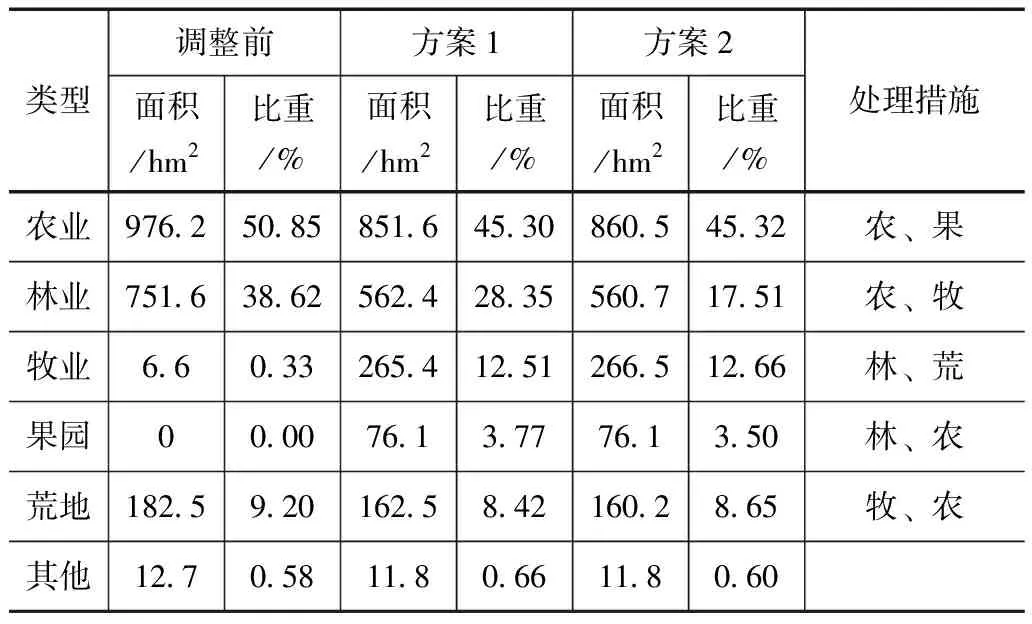
表3 在约束条件下的土地利用类型分配表

3 结论

(1)根据遗传算法多目标综合优化基本原理，通过将3个规划目标按照线性加权法进行求和，统一规划为单一目标进行求解。结合相关专家经验，将经济纯收入最大目标、粮食产量最大目标以及土壤流失最小目标分别进行重要性排列，其重要性系数分别为α1为0.6，α2为0.2，α3为0.2。

(2)在满足文中所述的约束条件下使得农业土地利用更加合理，采取修砌梯田、结合地形结构改为横坡垄耕等关键性技术措施将有利于提高土壤有机物含量增加土壤肥沃力；模型实现了流域的综合效益最优，并有效降低了水土流失带来的危害，明显提高了居民的生活水平和人均经济收入，生态系统得到改善，经济增长得到保障。

(3)将约束条件稍微进行改变，则该小流域的总体经济效果可获得更大收益，方案2的综合经济效益优于方案1。