基于熵权法与正态云模型的大坝安全综合评价
黄小梅,温明浩
(1.海城市上英水库管理处,辽宁 鞍山 114200;2.海城市水利技术推广中心,辽宁 鞍山 114200)
目前为止,我国完成各类水库的修建已9万余座,其中在建或已建高度在30m以上的大坝约5000余座,此类大坝水库工程在保证航运交通、农业灌溉、防洪排涝、发电等方面具有重要作用,并取得了较为显著的综合效益。据不完全统计,相当一部分大中型水利工程在不同程度上表现出病危状态。并且由于独特的环境气候和地理位置,我国东北部地区对坝高、库大、水利工程的修建逐渐呈增大趋势,并且此类水库多处于严寒的高山峡谷区域,甚至处于地震频发区域,所以对此类已建水利工程进行安全评价对于确保工程设施正常效益的发挥、促进区域经济发展具有重要意义。当前,国内外学者分别从多个角度对大坝安全评价开展研究并取得了一定成果,如苏怀智等[1]对大坝工作形态利用模糊可拓法进行了评估;王泉等[2]对大坝寒冬的安全状态利用模糊可拓法进行了定量的评估;伍元等[3]对大坝的安全形态采用熵理论进行了评估;刘天祥等[4]结合工程实际状况对某大坝的安全状态利用AFSA-AHP模型进行评估。上述评价方法虽然取得了一定的成果并得出了相应的理论,然而对评价指标的随机性和模糊性与大坝安全评价结果之间的作用关系并未进行深入研究。云模型是在M-Zade范式模糊数学改进的基础上发展而来的一种数学模型,它可对模糊性和随机性相结合的问题进行较好的分析处理,具有一定的普遍适用性。云模型经过多年的发展和实际应用已成为比较成熟、系统、全面的新的认知型模型[5]。熵权法是一种可降低人为干扰对评价结果作用影响的客观赋权法,其评价结果能够较好地反映实际状况,具有客观、公正、全面、科学基本特征并因此得到较为广泛的应用[6]。据此,文章依据云模型和熵权法基本理论建立了大坝安全综合评价模型,并结合实际工程相关数据利用模型对其进行了综合评价,对模型的有效性、可靠性、科学性进行了验证和分析。
1 理论分析
1.1 熵权法
引入m,n分别作为每个指标的观测值和大坝安全评价指标,其中第i个指标的第j个观测值采用xij进行表征。因此可建立指标值矩阵X,其表达式如下:
X=[xij]m×n
(1)
为消除不同指标单位和量纲的差异造成的不可通透性,需将上述矩阵进行归一化处理并得到标准矩阵Y,其表达式如下:
Y=[yij]m×n
(2)
式中,yij—对应于xij经归一化处理后的数值。
可利用下述公式对第i项评价指标的熵ei进行计算:
(3)
式中,k—标准系数,可利用k=lnn进行求解。
因此,各评价指标的权重ωi可采用下式进行计算:
(4)
依据上述计算结果可构建各指标权重向量矩阵W,如下所示:
W=(ω1,ω2,…,ωn)
(5)
上述中熵值ei越趋近于1,则代表评价指标权重可随任意指标熵值的改变而显著变化的程度。以熵ei值为(0.9725,0.9538,0.9638),各指标所对应的权重为(0.165,0.342,0.493)为例,权重在各指标熵值接近时可发生显著的变化,因此采用下述公式对权重计算公式进行调整:
(6)
式中,et、ei、el—分别为第t、i、l个指标的熵值。
1.2 云模型基本理论
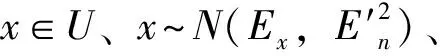
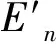

(7)
(4)对上述过程进行迭代计算,直至符合相关要求则计算终止。
1.3 大坝安全综合评价模型
可按照下述过程和方法建立基于正态云模型和熵权法的综合评价模型,其具体过程如下:
(1)分别构建大坝安全评价指标域和标准域,即C={c1,c2,,cn};S={s1,s2,,sn}。
(2)对大坝评价指标的权重矩阵W利用公式(6)进行计算。

(8)
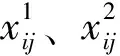
(9)
对上述公式进行求解转换有:
(10)
(4)云滴之间的离散程度可通过超熵Heij即熵的熵进行表征,云滴之间的凝聚性随超熵值的增大而提高,正态云模型在超熵值降低为0时,则转化为正态云曲线,按照经验对相关参数进行取值。
(5)对上述参数进行确定后可采用正向云发生器对各指标值进行求解并对大坝安全进行评价。首先对每个评价等级中各安全评价指标的隶属度向量矩阵Z=(zij)n×m进行求解,考虑到隶属度矩阵具有一定随机性并避免极端情况的发生,文章采用加权平均法对隶属度进行N次重复计算并确定最终平均综合隶属度,公式如下:
(11)
(6)利用权重矩阵W和隶属度矩阵Z计算结果可对评价标准域S上的模糊子集F进行求解,公式如下:
F=WZ=(f1,f2,,fm)
(12)
式中,fj—安全评价结果隶属于第j个评价等级的隶属度。结合相关文献最大隶属度原则,文章采用隶属度最大的评价等级作为水坝安全评价结果。
2 实例应用
2.1 大坝安全评价指标体系
某混凝土重力坝死水位和正常蓄水位分别为1760m和1820m,最大坝高为310m,总库容和调节库容分别为76.2×108m3和50.1×108m3,电站装机容量为4200MW且为年调节水库。为获得更多的监测资料并更加高效、全面地获取大坝的工作状态,在水利大坝建设施工期布设了多个观测检验装置如环境温度、变形、裂缝、渗流量、应力应变、裂缝、渗流、扬压力、上游水位、引张线、垂直监测等仪器装置[8-10]。结合已有观测数据资料和混凝土重力坝基本特性,分别从环境、渗流和大坝变形3个主要方面筛选出了具有代表性的8个安全评价指标,评价指标体系和评价标准见表1和表2。
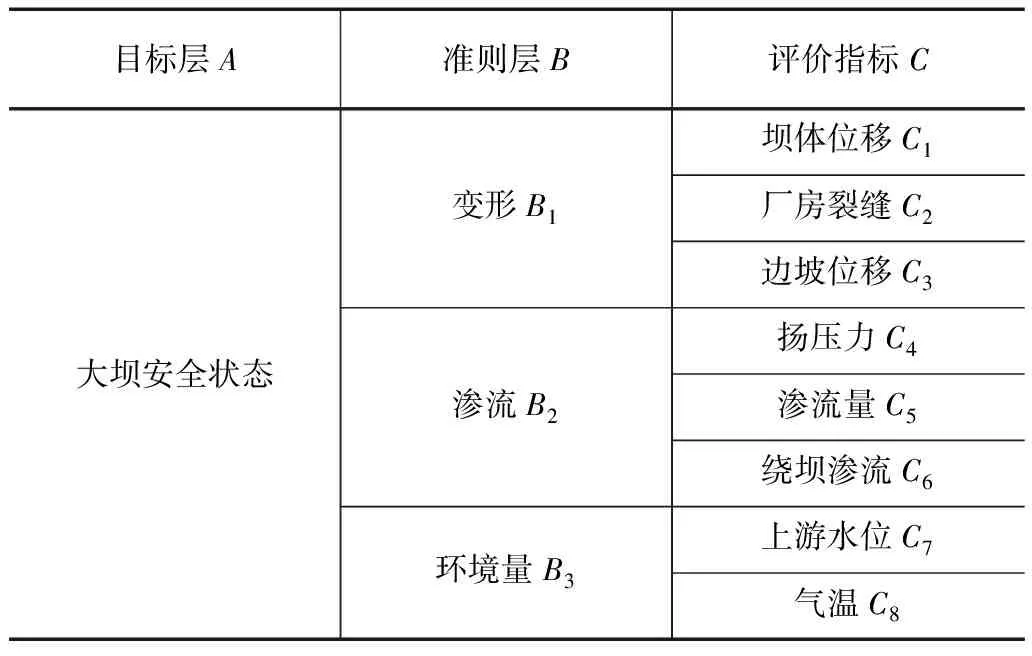
表1 大坝安全评价指标体系

表2 大坝安全评价指标标准
利用帷幕折减系数对表2中扬压力指标进行处理;将实际水位减去正常蓄水位作为上游水位指标;采用年平均气温与实际气温差值的绝对值作为气温评价指标值。表2中各评价指标均不存在明确的边界限定值,依据专家同样的建议、相关长期数据资料观测结果和反馈意见、相似工程的类比对各指标进行选取,因此大坝安全各评价指标具有一定的模糊性和随机性。针对上述特点和问题,采用云模型可进行很好的处理并具有较大的优势[11]。
2.2 评价结果
利用文中所述相关公式并结合评价指标标准和评价指标体系可对大坝安全评价的正态云模型参数矩阵进行求解,结果见表3。
选取C1评价指标进行隶属度函数分析,在不同评价等级下对评价指标C1的正态云参数利用Matlab平台进行隶属度函数求解。由表3计算结果可知,利用正向云发生器对大坝各指标实测值进行隶属度矩阵的求解,为使得计算结果具有更好的精度并考虑计算结果的随机性,文章对正态云模型参数进行100次迭代计算,各指标隶属度矩阵计算结果见表4。
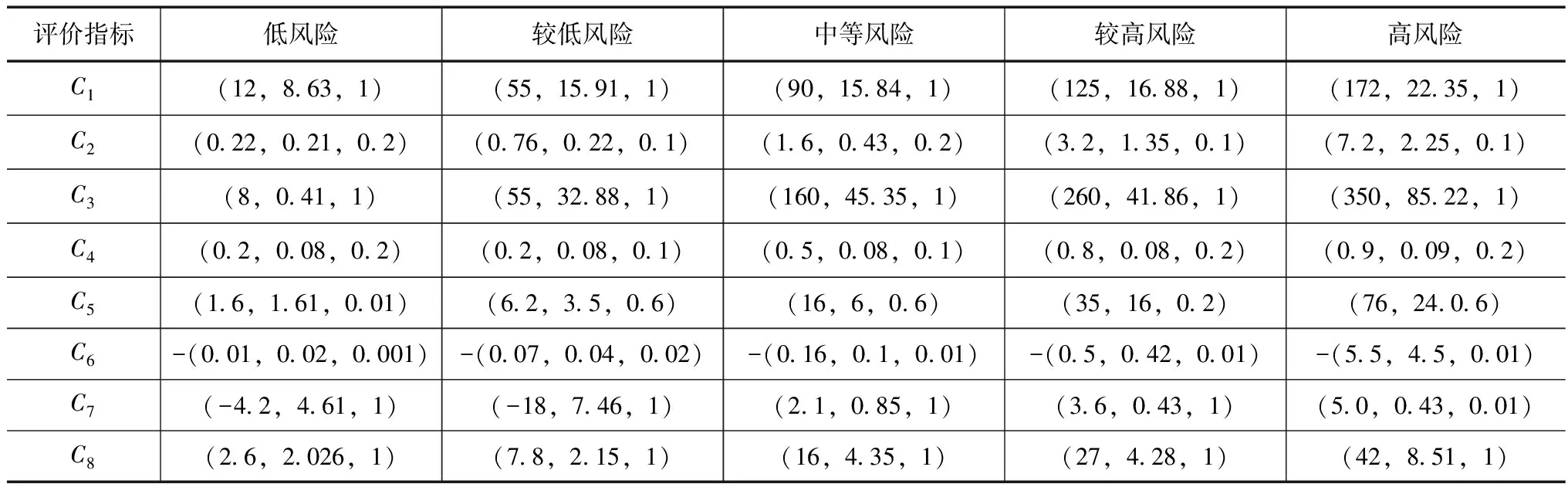
表3 正态云模型各评价指标计算结果

表4 各评价指标平均综合评估值计算结果
对大坝各指标权重利用熵权法和公式(6)进行求解,结果如下:
W={0.178,0.135,0.60,0.112,0.103,0.092,0.145,0.075}
利用表4以及各指标权重计算结果按照步骤5可对评价集上的模糊子集进行求解,结果见表5。

表5 大坝安全评价结果
由表5计算结果可知,该大坝处于较低的风险等级,结合大坝实际状况,其原因主要为环境和外部荷载对结构的影响作用时间较短,该水利大坝为新建大坝且投入运行时间较短,并且该大坝设计较为严格规范,施工养护及维护检修正常,大坝为大(1)型水利工程,其结构安全富裕程度较大且运行管理理念较为科学。现场实地勘测表明:该水利大坝未出现不可预期的渗水情况且在大坝内部和表面未存在裂缝,坝体结构运行正常。综上所述,大坝实际状况与模型安全评价结果具有良好的吻合度,模型评价结果能较好地反映坝体的实际状况,模型具有较强的可靠性与适用性。
3 结论
文章在详细分析了云模型和熵权法基本理论的基础之上构建了安全评价模型并运用于实际工程中,模型评价结果表明该大坝处于较低的风险等级。大坝运行实际状况与模型评价结果保持良好的一致性,其安全评价结果能够较好地反映坝体安全运行实际状况,模型具有较强的适用性与可靠性。

