三岔河上游流域径流演变特征与趋势预测研究
李长江,付 杰,陈文斌
(1.贵州省水利科学研究院,贵州 贵阳 550002;2.西北农林科技大学,陕西 杨凌 712100)
1 流域水系概况
三岔河流域位于贵州省西北部,为乌江流域南源一级支流,流域地势由西南向东北逐渐倾斜,东西高差大,南北高差相对较小。
三岔河干流全长325.6km,天然落差1397.9m,全流域面积7264km2。三岔河为典型山区河流,岩溶发育。流域水系发育,支流众多,呈羽状分布。
2 径流演变特征分析
2.1 径流年内变化特征
根据阳长水文站1958—2008年实测资料,多年平均径流逐月分配比例进行计算,得到各月在全年中的占比[1],见表1。

表1 阳长站径流逐月分配比例
从表1可知,三岔河上游流域径流主要集中在6—10月,径流占全年总径流的77.6%。全年径流比例以7月份的21.3%为最大,以3月份的1.9%为最小,其中将连续最大4个月的流量进行加和后得出,6—9月的径流占到了全年总径流的66.8%,连续最小4个月径流仅占全年总径流的8.8%,径流的年内分配十分不均匀。
2.2 径流年际变化特征
径流的年际变化采用极值比KM和变差系数CV来表示。通过对阳长站年径流极值的统计分析可知:1989年出现最小年平均流量为22.1m3/s,1997年出现最大年平均流量为62.3m3/s.径流的极值比KM和变差系数CV计算成果[2-3],见表2。
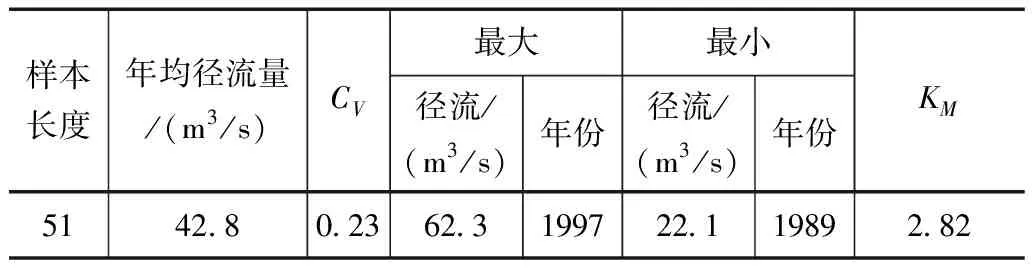
表2 径流多年变化特征参数
年径流的趋势分析主要是研究水文序列随时间的变化过程。受气候变化和人类活动的影响,多年径流序列会呈现出一定规律的变化趋势。若全过程都出现某种趋势,称这种趋势为整体趋势[4];若只在某一段时期出现了某种规律,则称为局部趋势。采用滑动平均方法、Mann-Kendall检验法和Spearman秩次检验法对流域的年径流变化趋势进行分析[5]。
2.2.1 滑动平均法
水文序列x1,x2,…,,xn(n为样本数),若逐个滑动,按一定步长取原序列中样本进行平均计算,可得到一个新序列yt,新序列使原序列更加光滑,易看出原序列的变化趋势。滑动平均法,其具体函数表达为:
(1)
式中,2k+1(k=1,2,…)—步长,即几年平均,k=1时为3年滑动平均。用滑动平均法对阳长站的径流序列进行滑动平均处理,分析成果如图1所示。
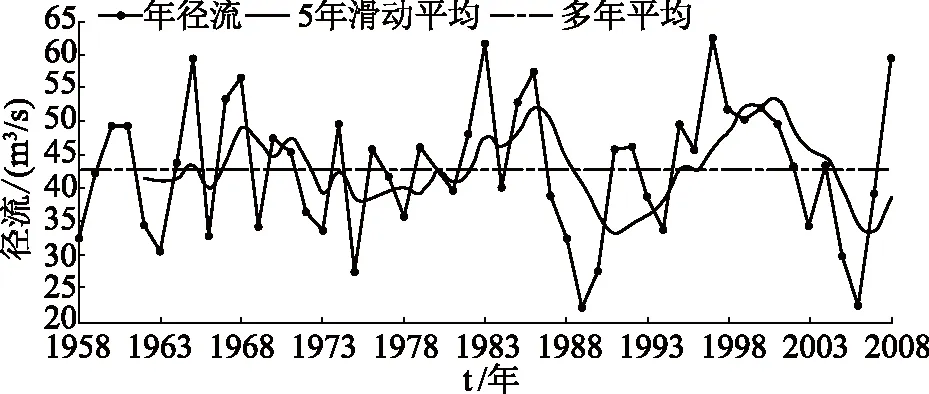
图1 径流演变特征曲线
从图1可知,阳长站年径流分时段趋势比较明显,即:1974—1986年呈上升趋势;1991—2001年上升趋势明显;1986—1991年、2001—2007年呈下降趋势。
2.2.2 Mann-Kendall秩次相关检验
对时间序列x1,x2,…,xn(n为样本数),对应观测值(xi,xj,j>i)中xi (2) 假设原序列无明显的变化趋势,给定显著化水平α(α=0.05),在正态分布临界值表中查出临界值Uα/2(U0.05/2=1.96),当|U| 2.2.3 Spearman秩次相关检验 分析径流序列xt与时间t的相关关系,建模时序列xt用其秩次Rt(即把序列xt从大到小排列后,xt所对应的序号)表示,t仍为时序(t=1,2,…,n)。秩次相关系数函数表达为: (3) 式中,n—样本长度,dt=Rt-t。秩次Rt与时序t越相近,dt越小,秩次相关系数越大,原序列的趋势越显著。 假设原序列无趋势,当给定显著水平α(α=0.05)后,在t分布表中查出临界值tα/2,当|T| 采用最近邻抽样回归模型和人工神经网络模型,分别从统计和人工智能的角度,以阳长站资料为基础,对流域年径流分别进行预测[6-7]。 序列时间{Xt}n,Xt依赖于前P个相邻历史值Xt-1,Xt-2,…,Xt-p。定义Dt=(Xt-1,Xt-2,…,Xt-p),称Dt为特征矢量,Xt为Dt的后续值(t=p+1,P+2,…,n)。从Dt中选取K个与待预测特征矢量最相似的矢量,记为D1(i),D2(i),…,Dk(i),其对应的后续值分别为X1(i),X2(i),…,Xk(i)。 K)。即Xj(i)对Xi的贡献越大。欧氏距离表达式为: (4) 式中,r′t(i)—Di与Dt间的欧氏距离;dij,dtj—Di,Dt的第j个元素;P—特征矢量维数。径流趋势预测基本方程为: (5) 神经网络模型模拟生物大脑的信息处理系统。在生物大脑中,神经元是信息处理的基本结构和功能单元,人工神经网络模型把节点模拟为神经元,通过节点连接输入层和输出层,通过比较输出层输出与期望输出的误差来调节各层之间的连接权重,通过反复迭代确定误差最小的连接权[8]。年径流预测,使用多层前馈网络的误差反向传播(Error Back Prorogation,简称BP)算法。三层BP网络拓扑结构,如图2所示。 图2 三层BP网络结构图 采用最近邻回归(NNBR)和人工神经网络(ANN)对三岔河阳长水文站1958—2008年的年平均流量进行预测,并与实测数据进行对比,其趋势预测结果如图3所示。 图3 年平均流量预测模拟结果 由图3可知,在进行年径流预测时,最近邻抽样模型的拟合合格率、检验合格率分别为87.5%和60%,人工神经网络模型的75.6%和60%;最近邻抽样模型拟合平均误差和检验平均误差分别为9.61%和27.3%,人工神经网络模型的14.02%和38.87%。 通过对流域径流演变趋势的分析,以及采用最近邻回归(NNBR)和人工神经网络(ANN)算法,对三岔河阳长水文站1958—2008年的年平均流量进行多时间尺度演变趋势预测,主要研究结论为: (1)流域内径流年内变化大,径流主要集中在6—10月,约占全年总径流的77.6%;长系列实测资料表明,流域内年际变化趋势呈不显著趋势。 (2)最近邻回归(NNBR)径流预测模型,其拟合合格率、检验合格率及准确率较ANN神经网络模型高,预测结果相对贴近实际。 (3)三岔河流域属中小流域,影响径流预测的因素较多,为更好开发利用好流域水资源,尚需对预测模型的权限约束条件及特征参数设置进行深层研究。3 径流趋势预测
3.1 最近邻回归(NNBR)
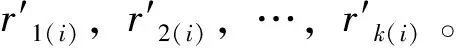
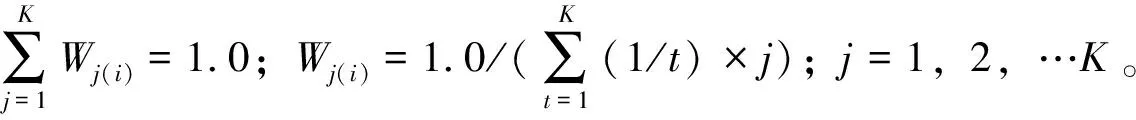
3.2 人工神经网络(ANN)
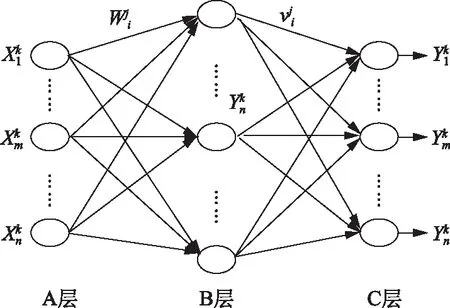
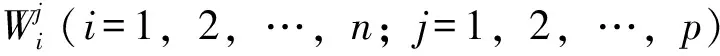
3.3 预测结果分析
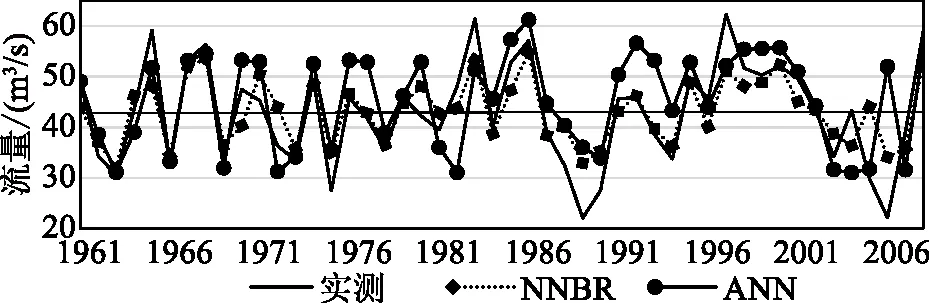
4 结论

