垂直线源灌土壤湿润体尺寸预测模型研究

范严伟 邵晓霞 王 英 龚家国

(1.兰州理工大学能源与动力工程学院， 兰州 730050； 2.中国水利水电科学研究院流域水循环模拟与调控国家重点实验室， 北京 100038)

0 引言

我国西北旱区土地资源丰富，日照充足，昼夜温差大，是发展林果业的理想区域[1]。然而，这些地区降雨量有限，果树生产在很大程度上取决于灌溉[2]。传统灌溉方式耗水量大、水分利用效率低，不利于生态经济的可持续发展[3-4]。因此，灌溉技术和水资源管理的改进将发挥重要作用。

垂直线源灌是一种适用于深根植物的节水灌溉方法，其灌水器垂直埋入土体，灌水过程中，水分直接进入植物根部，湿润体不易观测[5]。湿润体的形状及大小影响着植物的生长与产量，了解垂直线源灌湿润体动态变化特征，可确保灌水器在活性根区的精确放置，对设计经济高效的垂直线源灌溉系统至关重要[6-7]。土壤质地是决定灌溉设计参数的重要因素，地下灌溉系统的设计应考虑土壤质地的影响[8-12]；相同土壤质地条件下，土壤容重增加，孔隙度减小，土体入渗能力下降[13-16]；土壤初始含水率决定了渗透初期的土壤水势，土壤初始含水率增加，湿润体尺寸逐渐增大[5,11,17-20]。线源长度和直径决定了灌水器渗水界面的大小，线源长度或直径增大，渗水界面面积变大，意味着水分进入土壤的通道增加，导致相同时间内入渗水量增多，湿润体随之增大[21-24]。因此，从实用角度出发，线源直径既要尽可能的大以加快其渗水速率，提高灌水均匀度，又要尽可能的小以减弱对作物根系生长的影响。灌水器埋深直接改变湿润体水分分布位置，是实现作物根系与湿润体有效匹配的关键因素，埋深过浅会增加地表水分无效蒸发，埋深过深又会引起深层渗漏和表土水分亏缺[25-29]。因此，埋深应与土壤条件、根系分布及耕作要求等相适应。灌溉必须适时适量，灌水时间过早或过晚、灌水定额过大或过小都是无益的。DU等[2]研究表明，中国西北干旱区苹果根区土壤含水率低于田间持水率的50%～55%时，会对树木生长和最终产量造成水分胁迫；周罕觅等[30]研究水肥耦合对3年生苹果幼树生长、产量、品质及水肥利用的效应，得出灌水下限为田间持水率的65%～75%；贾俊杰等[31]指出，SH矮砧苹果幼树滴灌条件下适宜灌水下限为60%的田间持水率。孙三民等[32]通过小区试验，确定13 L/(棵·次)的灌水量为适宜的新疆红枣间接地下滴灌灌溉模式；张陆军等[33]指出，陕北山地梨枣树涌泉根灌时，每株2个灌水器及每个灌水器40 L/(株·次)的灌水量组合是适宜的布置方式；吴悠等[34]通过遮雨棚下可称量式蒸渗桶试验得出，生育期内8.4 L/(株·次)为柱状苹果树相对节水的灌溉模式。

湿润体动态变化可通过湿润锋距离量化表征。国内外学者开发了一些用于确定湿润锋距离的模型，其中，最常见的是分析模型[21,35-38]、数值模型[39-40]和经验模型[11,41-45]。通常，通过求解特定初始和边界条件的控制方程(Richards方程)来开发分析模型和数值模型，而使用实验或数值模拟的回归分析来开发经验模型。文献[46-48]对数值和经验模型进行了比较和评估，研究表明，HYDRUS模型计算结果能较好地反映土壤水分运动基本规律，但模型较复杂，需输入大量参数才能模拟计算；另外，每个经验模型都是土壤水力特性和灌溉参数的函数方程，形式较简单，但仅适用于具体的灌溉技术，如开发的滴灌或沟灌湿润体预测模型并不适用于垂直线源灌。因此，有必要开发一种可以预测垂直线源灌土壤湿润体尺寸的经验模型，为确定适宜的灌水技术参数和实现灌溉系统优化运行提供实用而方便的手段。

数值模拟方法可对不同土壤特性、不同灌水器规格和不同设计参数条件下的土壤水分运动过程进行模拟[49-51]。李淑芹等[52]、FAN等[53]通过试验验证了垂直线源灌HYDRUS-2D模拟结果的有效性。基于此，本文采用HYDRUS-2D软件，模拟研究土壤质地、初始含水率、线源长度、线源直径和线源埋深对垂直线源灌湿润体运移特征值的影响；利用模拟数据筛选影响湿润体运移的主导因素，进而构建预测湿润体尺寸的简化经验模型；最后，通过土箱试验验证经验模型的可靠性。

1 材料与方法

1.1 试验设计

试验装置由3部分组成：土箱、马氏瓶和线源灌水器，如图1所示。土箱由10 mm厚有机玻璃制成，长×宽×高为50 cm×50 cm×100 cm。土箱底部留有多个通气孔(直径2 mm)，以防气阻发生。线源与土箱接触面开取土孔(直径2 cm，间距5 cm)，用于测量灌溉结束时的土壤含水率。线源采用1/4圆柱体，底端密封，管底向上l长度的柱面均匀开孔。马氏瓶直径为10 cm，高度为100 cm。试验前，将供试土样按设定的初始含水率加水，均匀混合后，用塑料薄膜密闭静置1 d，待土壤水分分布均匀后，按设计容重分层(5 cm)装入土箱，以获得均匀土壤剖面。为了便于观察土壤湿润体变化过程，将线源灌水器用纱布包裹，并置于土箱一角，确保灌水器管壁与土壤紧实接触，待次日进行入渗试验。试验中，马氏瓶提供恒定水头，按先密后疏的时间间隔记录累积入渗量，并用马克笔绘制湿润锋运移图。入渗达到设定灌水定额后停止供水，迅速从灌水器两侧预留孔取土，用干燥法(105℃干燥24 h)测定土壤含水率。为尽量消除试验误差，每个试验重复3次。

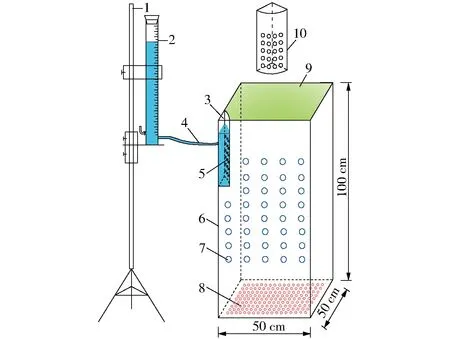
图1 垂直线源灌试验装置及灌水器细部结构Fig.1 Experimental equipment for vertical line source irrigation and detailed structure of emitter1.调节水头支架 2.马氏瓶 3.灌水器 4.橡胶管 5.渗水孔6.土箱 7.取土孔 8.通气孔 9.土壤表面 10.灌水器细部结构

参照文献[2,30-34]研究成果，取民勤地区砂壤土(容重γd=1.45 g/cm3，田间持水率θf=0.332 cm3/cm3，饱和导水率Ks=0.039 cm/min)和风沙土(γd=1.56 g/cm3，θf=0.051 cm3/cm3，Ks=0.345 cm/min)，每种土壤采用2种处理(初始含水率θ0=60%θf、线源直径d=4 cm、线源长度l=20 cm、线源埋深b=40 cm、灌水量V=40 L；θ0=70%θf、d=6 cm、l=30 cm、b=50 cm、V=40 L)进行垂直线源灌土壤入渗试验。

1.2 数学建模

1.2.1基本方程

假设土壤是均匀和各向同性的，垂直线源灌可概念化为轴对称的三维入渗过程。使用HYDRUS-2D模拟[54]。土壤水分运动控制方程为Richards方程

(1)

式中r——径向坐标值，cm

z——垂向坐标值，cm，向下为正

θ——土壤含水率，cm3/cm3

h——压力水头，cm

t——时间，min

K(h)——土壤非饱和导水率，cm/min

采用van Genuchten-Mualem(VG-M)方程[55-56]描述土壤水分特征曲线和非饱和导水率

(2)

(3)

其中

m=1-1/n

式中Se——土壤相对饱和度

θr——土壤残余含水率，cm3/cm3

θs——土壤饱和含水率，cm3/cm3

α——与进气值成反比的经验参数，cm-1

n、m——影响土壤水分特征曲线形状的经验常数

1.2.2定解条件

图2(图中A、B、C分别为线源最高点、最低点和中心点)为本研究中用于模拟不同建模情景的初始和边界条件。

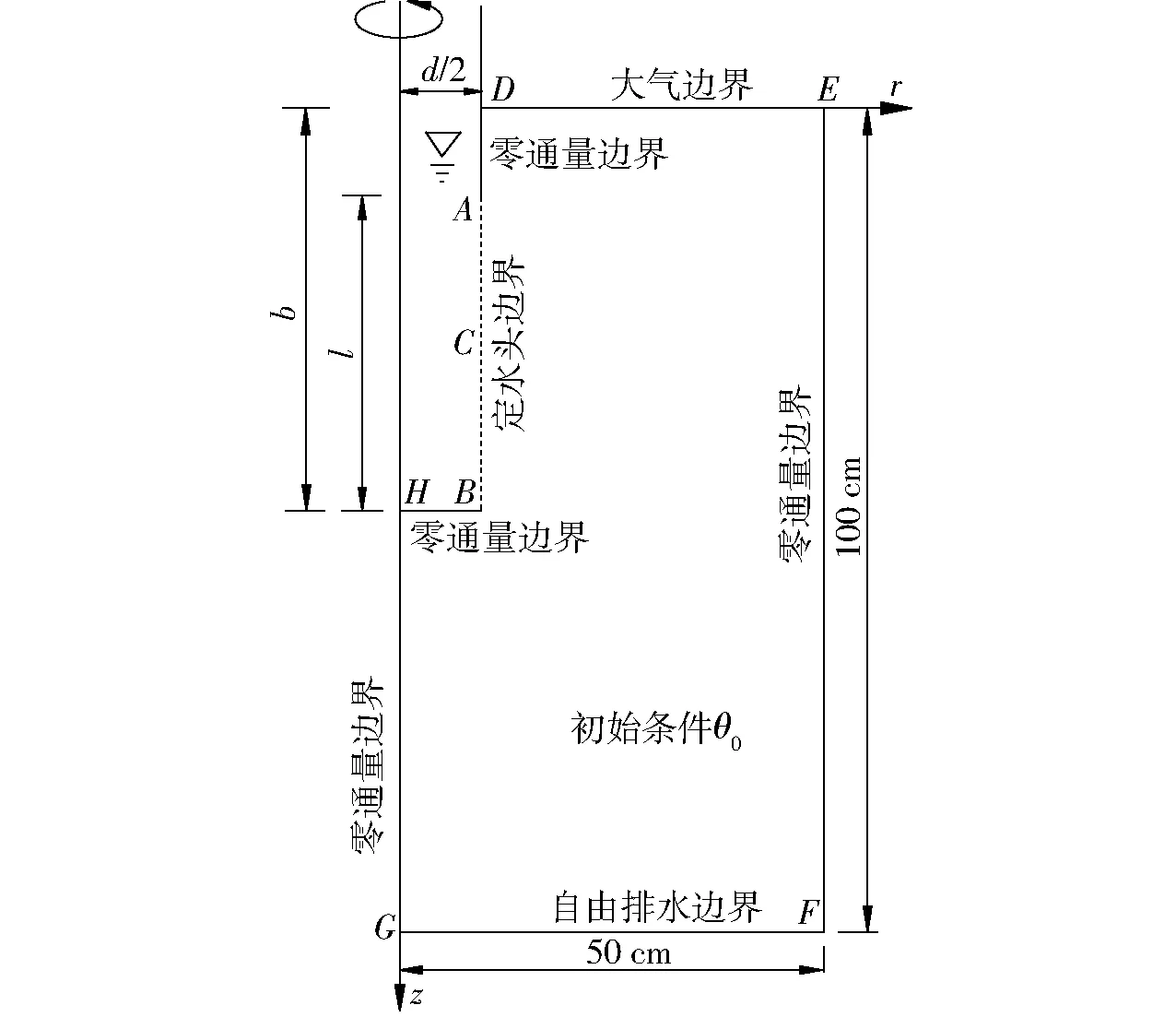
图2 具有初始和边界条件的计算域Fig.2 Computational domain with initial and boundary conditions

在所有的模拟情景中，土壤含水率按初始含水率设置；上边界DE受大气条件影响，考虑灌水过程中地表为干土层，蒸发量很小，为简化计算，按零通量面设置；下边界FG不受灌水影响，为自由排水，按零通量面设置；左边界GH为灌水器中心轴，AD为塑料管壁，均无水量交换，按零通量面设置；右边界EF灌溉水未到达，按零通量面设置；线源底部BH密封，为零通量边界；渗水面边界为充分供水方式，供水开始后很快达到饱和，可按定水头边界处理[20,22]。

综上，初始条件可表述为

(4)

式中θ0——土壤初始含水率，cm3/cm3

Ω——计算域(图2)

边界条件可表述为

(5)

1.2.3模拟方案

采用单因素分析法，设置81种情景，模拟分析不同土壤质地(表1)、θ0(50%θf、60%θf、70%θf)、d(2、4、6 cm)、l(10、20、30 cm)和b(30、40、50 cm)等因素对垂直线源灌湿润体的影响。土壤质地VG-M模型参数取自CARSEL等[57]资料以及文献[52]，如表1所示。

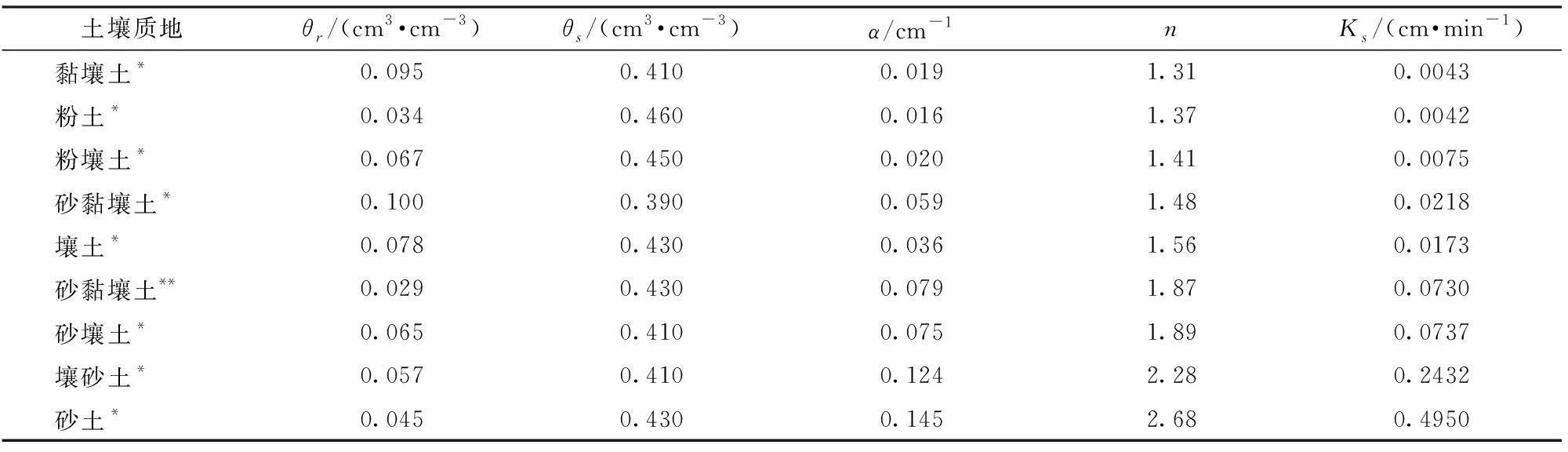
表1 HYDRUS模拟中9种典型土壤的VG-M模型参数Tab.1 VG-M model parameters of nine typical soils in HYDRUS simulation

注：*表示取自文献[57]，** 表示取自文献[52]。

不同质地土壤田间持水率采用RAB等[58]建立的预测模型获得，具体表达式为

(6)

式中θp——凋萎系数，可采用VG-M模型参数中的θr表示[11]，cm3/cm3

1.2.4求解方法

利用HYDRUS-2D进行数值求解。求解过程中，采用隐式差分格式进行时间离散，Galerkin有限元法对土壤剖面进行空间离散。考虑到田间实际和计算精度的要求，确定有限单元计算域深度为100 cm，宽度为50 cm，空间步长为1 cm，时间步长为0.1 min，模拟历时由灌水定额(40 L)决定。

1.3 分析方法

垂直线源灌湿润体形状近似为“梨”型[22,52]。选取5个特征值(A点水平方向、B点水平方向、C点水平方向、C点垂直向上和C点垂直向下)勾画出湿润体轮廓，点A、B和C见图2。研究表明地下三维入渗土壤湿润锋运移过程可采用幂函数描述，且具有很高的精度[22,59-61]。因此，采用幂函数定量分析垂直线源灌土壤湿润锋运移过程，其具体表达式为

UC=l/2+b1ta1

(7)

DC=l/2+b2ta2

(8)

RA=d/2+b3ta3

(9)

RB=d/2+b4ta4

(10)

RC=d/2+b5ta5

(11)

式中UC、DC——C点垂直向上、垂直向下湿润高度，cm

RA、RB、RC——A、B、C点湿润半径，cm

a1、a2、a3、a4、a5、b1、b2、b3、b4、b5——拟合参数

根据模拟结果分析湿润体运移规律，探讨影响机理，筛选主导因素，采用式(7)～(11)拟合获得a1、a2、a3、a4、a5、b1、b2、b3、b4和b5值，研究拟合参数与主导因素间的量化关系，进而建立垂直线源灌土壤湿润体运移距离模型。

1.4 误差分析

选取4个指标，即平均绝对误差MAE、均方根误差RMSE、偏差百分比PBIAS和纳什效率系数NSE，对湿润体尺寸的实测值和预测值进行误差分析。指标参数定义为

(12)

(13)

(14)

(15)

式中EMAE——平均绝对误差

EPBIAS——偏差百分比

ENSE——纳什效率系数

Mi——第i个实测值

Si——第i个模拟值

Mmean——实测值的平均值

N——数据总个数

MAE和RMSE的数值越接近0，PBIAS为[-10，10]，NSE越靠近1，表示模拟值与实测值差异越小，两者吻合越好[62]。

学生又活跃起来，当tan (α2-α1)不存在时，应是右边分母为零时，即1+k1k2=0，从而k1k2=-1．也可以这样说，如果1+k1k2≠0，则tan (α2-α1)有意义，而tan (α2-α1)没意义，所以必有1+k1k2=0．

2 结果与分析

2.1 拟合参数a1～a5影响因素分析

2.1.1拟合参数a1

利用HYDRUS-2D模拟结果，采用式(7)，拟合获得不同影响因素下a1，如图3所示。

图3 拟合参数a1随饱和导水率Ks的变化规律Fig.3 Variations of fitting parameter a1 with saturated hydraulic conductivity Ks

由图3可见，相同Ks时，拟合参数a1主要受线源长度和埋深的影响，而土壤初始含水率和线源直径对其影响较小。主要是线源长度和埋深影响湿润锋到达地表的时间，线源越长或埋深越浅，湿润锋到达地表时间越短，导致拟合参数a1时数据量减少，产生了拟合误差。不同Ks情况下，拟合参数a1随Ks先增大后减小，但增减幅度不大(0.172～0.355)，为简化计算，可取平均值，即a1=0.3。

2.1.2拟合参数a2

利用HYDRUS-2D模拟结果，采用式(8)，拟合获得不同影响因素下a2，如图4所示。

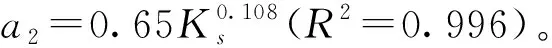
图4 拟合参数a2随饱和导水率Ks的变化规律Fig.4 Variations of fitting parameter a2 with saturated hydraulic conductivity Ks

图5 拟合参数a3随饱和导水率Ks的变化规律Fig.5 Variations of fitting parameter a3 with saturated hydraulic conductivity Ks

2.1.3拟合参数a3

利用HYDRUS-2D模拟结果，采用式(9)，拟合获得不同影响因素下a3，如图5所示。

由图5可见，土壤初始含水率、线源直径、线源长度和埋深对拟合参数a3影响较小。不同Ks情况下，拟合参数a3随Ks先增大后减小，但增减幅度不大(0.269～0.381)，为简化计算，可取平均值，即a3=0.348。

2.1.4拟合参数a4

利用HYDRUS-2D模拟结果，采用式(10)，拟合获得不同影响因素下a4，如图6所示。

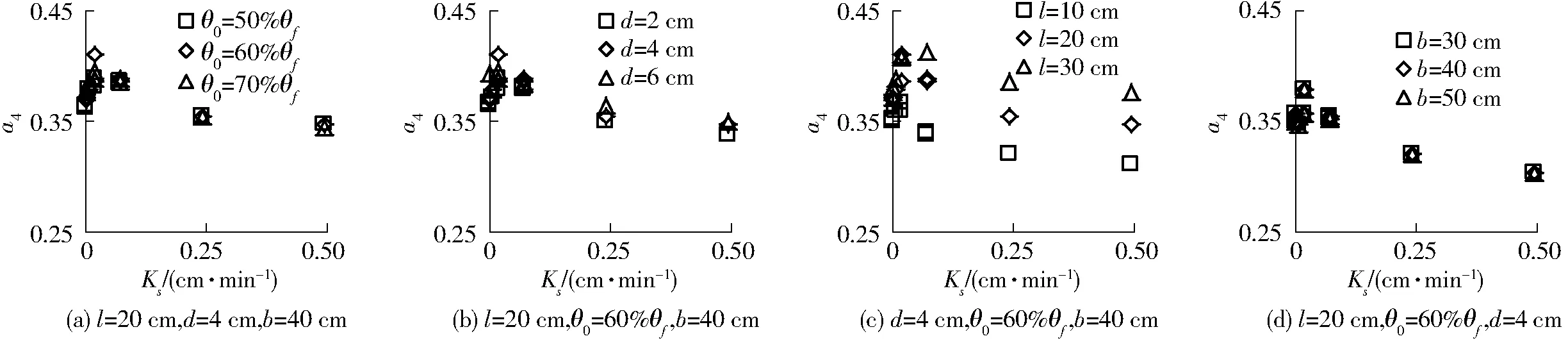
图6 拟合参数a4随饱和导水率Ks的变化规律Fig.6 Variations of fitting parameter a4 with saturated hydraulic conductivity Ks

由图6可见，相同Ks时，拟合参数a4主要受线源长度的影响，而土壤初始含水率、线源直径和埋深对其影响较小。线源越长，其渗水速率越快，导致湿润体水分叠加效应增强，同时，由于重力势的作用，下部湿润体的叠加效应强于上部。不同Ks情况下，拟合参数a4随Ks先增大后减小，但增减幅度不大(0.298～0.414)，为简化计算，可取平均值，即a4=0.374。

2.1.5拟合参数a5

利用HYDRUS-2D模拟结果，采用式(11)，拟合获得不同影响因素下a5，如图7所示。

由图7可见，类似于拟合参数a4，相同Ks条件下，拟合参数a5主要受线源长度的影响，不同Ks情况下，拟合参数a5随Ks先增大后减小，但增减幅度不大(0.278～0.379)，为简化计算，可取平均值，即a5=0.346。

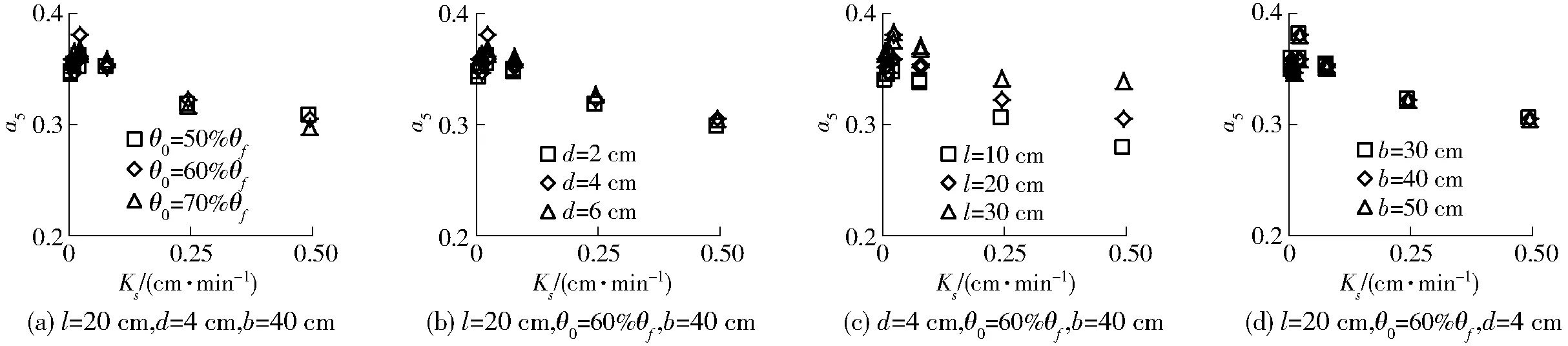
图7 拟合参数a5随饱和导水率Ks的变化规律Fig.7 Variations of fitting parameter a5 with saturated hydraulic conductivity Ks

综上所述，拟合参数a1、a3、a4和a5随Ks、θ0、d、l和b的变化规律不明显，且变化幅度较小。为简化计算，分别取其平均值。a2随θ0、d、l和b的增减而稍有变化，但变化较小，而随Ks的增大而增大，两者具有较好的幂函数关系。

将a1～a5分别代入式(7)～(11)，得

UC=l/2+b1t0.300

(16)

(17)

RA=d/2+b3t0.348

(18)

RB=d/2+b4t0.374

(19)

RC=d/2+b5t0.346

(20)

2.2 拟合参数b1～b5影响因素分析

利用HYDRUS-2D模拟结果，采用式(16)～(20)，再次拟合获得不同θ0、d、l和b组合下的b1～b5，如图8所示。

由图8可见，拟合参数b1、b2、b3、b4和b5均随Ks的增大而增大，θ0、d、l和b对其影响相对较小。进一步分析发现b1、b3、b4和b5与Ks具有很好的幂函数关系，而b2与Ks呈线性关系。基于此，可得垂直线源灌湿润体尺寸简化预测模型，即

(21)

(22)

(23)

(24)

(25)

2.3 模型验证

利用试验数据对简化预测模型进行验证。将砂壤土和风沙土的Ks分别代入式(21)～(25)，得2种土壤的垂直线源灌湿润体尺寸简化预测模型为：

民勤砂壤土

(26)

民勤风沙土

(27)

将简化预测模型计算值与试验特征值(2个处理，3个重复)进行对比分析，如图9所示。

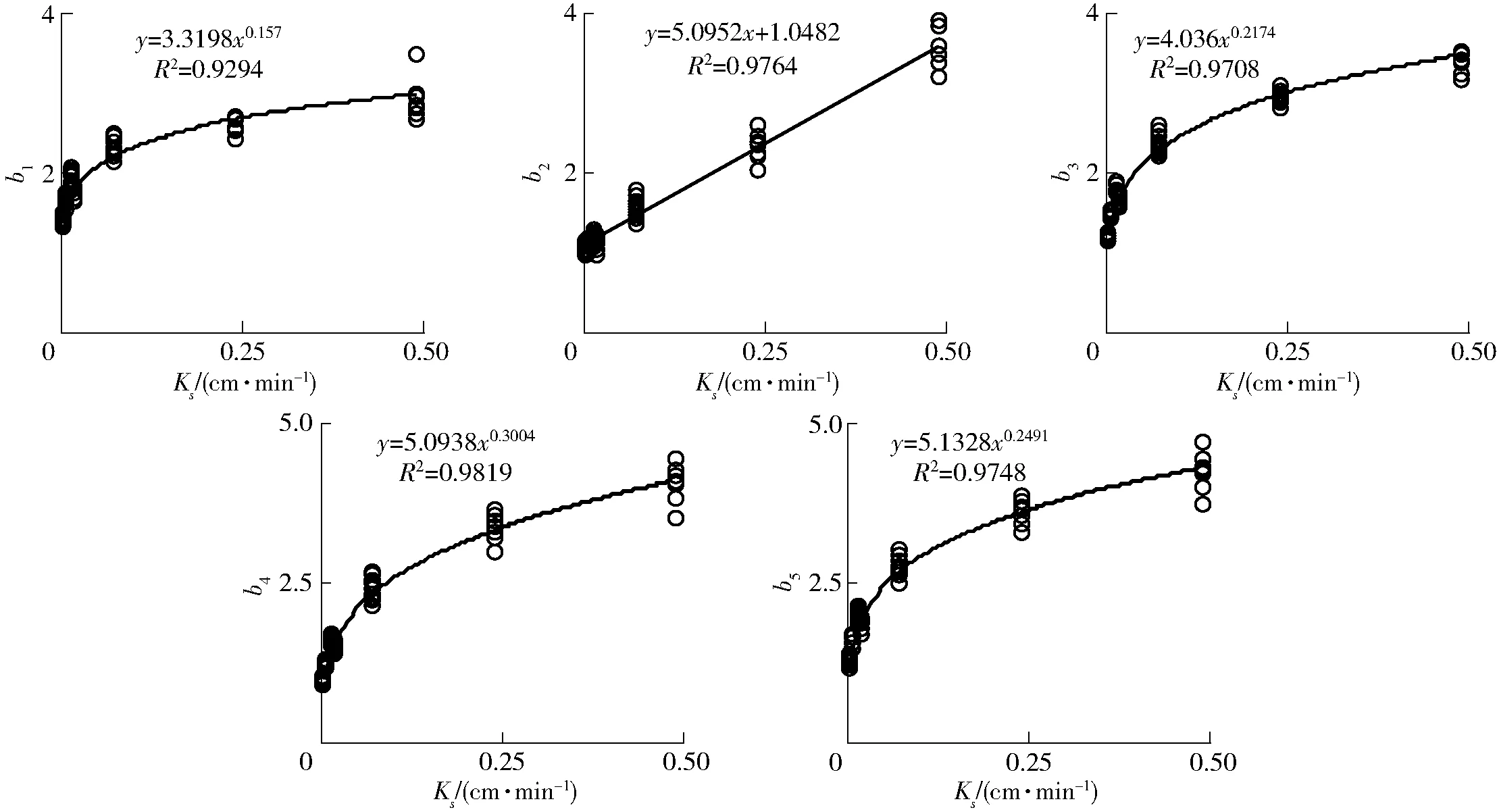
图8 拟合参数b1～b5随饱和导水率Ks的变化规律Fig.8 Variations of fitting parameter b1～b5 with saturated hydraulic conductivity Ks

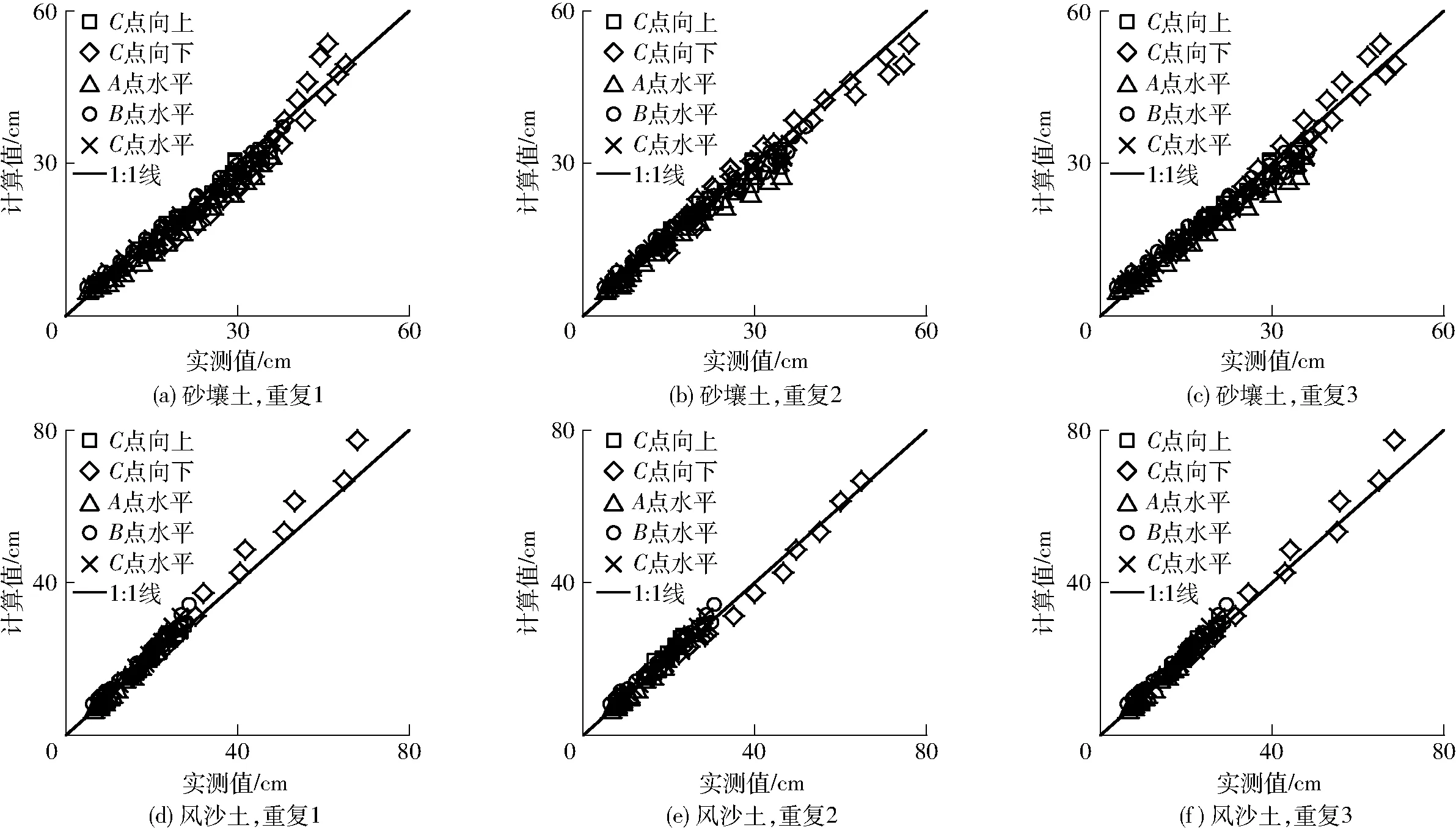
图9 2种土壤垂直线源灌土壤湿润体尺寸计算值与实测值对比Fig.9 Comparisons of calculated and measured values of wetted soil dimensions for two soil types undervertical line source irrigation

采用式(12)～(15)，对计算值与实测值进行统计分析，计算结果见表2。

由表2可知，MAE和RMSE接近0，PBIAS为-4%～9%之间，NSE靠近1(NSE不小于0.929)，说明简化预测模型计算值与实测值一致性良好，但仍存在一定误差，究其原因可能是垂直线源灌土壤湿润锋运移距离受土壤质地影响最大，而土壤初始含水率以及线源直径、长度和埋深对其尚有一些影响，为了简化计算，仅考虑了土壤质地的影响，建立了单变量模型，从而在一定程度上影响了计算结果的准确性。另外，仅采用饱和导水率Ks来表征不同土壤质地湿润锋运移规律也是存在部分误差的原因之一。

表2 计算值与实测值统计分析Tab.2 Statistical analysis of calculated and measured values

3 结论

(1)垂直线源灌湿润体尺寸主要受土壤质地影响，土壤质地越粗(Ks越大)，湿润锋运移越快；线源长度、线源直径和埋深对其影响较小。

(2)土壤湿润锋运移过程符合幂函数关系，幂函数系数随Ks的增大而增大，幂函数指数在垂直向上和水平方向上变化较小，而在垂直向下方向上随Ks的增大而增大。

(3)提出了包含Ks的垂直线源灌土壤湿润体尺寸预测模型，利用试验验证了预测模型的有效性，初步实现了由土壤物理参数预测垂直线源灌土壤湿润锋运移距离的可能。