浅海浮式栈桥锚碇系统布链方式比较

赵晶

(海军研究院海防所,山东青岛 266100)

随着我国海洋经济建设的发展，沿海地区的浅海水域开发建设越来越广泛,但水深极浅的浅海水域给大宗货物上岸带来了极大麻烦，如能建设大型的海上浮式平台并通过浅海浮式栈桥与浅海滩涂连接，可为解决这一难题提供一种便捷有效的方法[1-2]。海上浮式栈桥能否成功应用，在很大程度上取决于锚定技术是否可靠[3-5]。与此相关的内河浮桥的锚定技术早已有了充分的研究和成熟的设计理论，但海上浮式栈桥常常受到风、流、浪等使用环境因素及珊瑚礁盘的地质条件的影响[6-7]，海上浮式栈桥的锚定技术与内河浮桥有一定的不同，故本文对浅海浮式栈桥锚碇系统的布链方式进行进一步研究[8]。

1 实体参数及建模

图1 单桥节浮箱的主体尺寸及波向角定义

1.1 浅海浮式栈桥的实体参数

浅海浮式栈桥入海端连接靠泊平台，连岸端连接卸载平台，中间由3节桥节连接而成，每一个桥节即为一个巨大的浮箱，浮箱高1.8 m，吃水深度约为0.36 m，其主体平面尺寸如图1所示。

1.2 建模

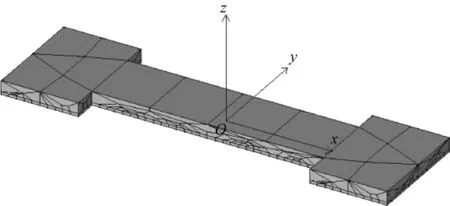
图2 浮箱计算模型

根据浮箱的主要技术参数，图1中的xOy平面为水面，采用ANSYS软件中的壳单元shell63对单个浮箱进行建模。由于利用AQWA-LINE对浮箱的附加质量、辐射阻尼、衍射力数据以及每个波长、每个波浪方向上的漂移力等进行计算时[9]，水面线以下部分对计算精度有很大影响，故在划分网格时，以水面线为基准对浮箱的计算模型进行分割，将水面线以下部分划分为较为细密的网格，水面线以上部分划分为较大的网格[10]。

通过ANSTOAQWA命令将节点和单元信息导出，再用于AQWA-LINE计算的卡片式输入文件中，输入投锚点坐标数据并修改其他计算参数，建立浅海浮式栈桥的计算模型。导入至AQWA中的模型如图2所示。

2 荷载施加与布链方式

2.1 荷载施加的方法

浅海浮式栈桥的作业条件为3级海况，风速相当于蒲福风级5～6级，流速1.5 m/s，波高1.0 m。锚碇系统布链方式和预张力与单个浮式栈桥桥节所受的荷载有关。浅海浮式栈桥的外部荷载主要有风荷载、水流荷载和波浪荷载，荷载的大小和方向对单个浮式栈桥桥节的运动和锚碇系统的受力有很大影响。由于浅海浮式栈桥是用于浅海水域建设时的临时性施工便桥，无重载车辆通行和频繁的车辆行驶，对布链方式的选择影响极小，故在计算时忽略了垂向荷载的作用。

在施加波浪荷载时，导入了JONSWAP波浪谱，并可以根据不同的设计要求和外部环境条件来定义波浪的波高和波向等参数。绝大部分的海岸带水域由海向陆逐渐变浅，由于波浪的折射作用，无论波浪初始传播方向如何，随着水深变浅，都有逐渐转向垂直于海岸向岸推进的趋势[11]。但由于浅海水域的浅水区宽度不足，又考虑到浅海浮式栈桥向海中延伸了一段较长的距离，波浪的这种近岸效应难以使波向角完全达到0°，故在数值模拟时可将波浪荷载的波向角假定为30°，波向角的定义如图1所示。

波浪在礁盘边缘破碎后，演变为上岸流和顺岸流，方向即为0°和90°，由于浮箱浮于水面且吃水较浅，仅按照水面处的流速进行了定义。在施加风荷载时，采用NPD风谱，同样可根据设计要求和环境条件定义高度为10 m处的风速和风向等参数。由于风荷载方向更加多变，出于设计安全的考虑，使风荷载与波浪荷载、流荷载方向相同，形成相互叠加的效应，故选取风荷载方向为0°、30°、90°三种方向进行计算分析。

2.2 布链方式

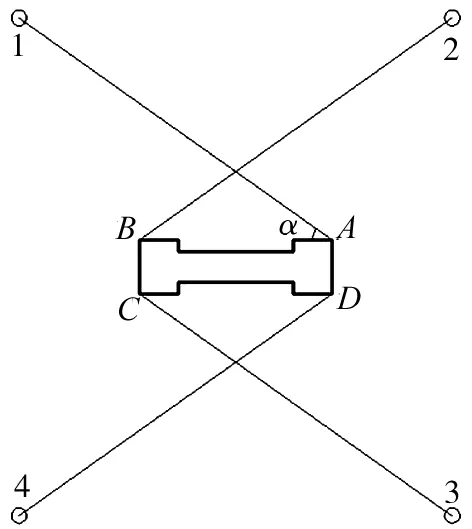
图3 α示意图

对于浅海浮式栈桥布链方式的研究目前并没有具体的理论，相关研究尚在探讨阶段[12-15]。文献[16]通过计算发现，锚泊线夹角为22.5°～67.5°的锚碇系统布置方式的系统回复力显示出方向上的平稳性，而夹角为40°～60°，45°～60°提供的系统回复力随着波浪方向的变化而变化。文献[17]根据潮流实验电站的实际锚泊布置需要，讨论了复杂海底地形的锚泊定位系统设计方法，并根据环境要求设计了4条锚泊线组成的锚泊阵列，锚泊线的张角根据近岸和离岸两侧水深不同而采用不同的角度。锚泊线的最优夹角应处于一定范围之内，而且会根据环境条件和水深的不同而变化。由于在浅海水域无法使用大型的施工船舶，施工作业面临很多困难，所以要尽量减少投锚的次数以方便施工，因此每个浮箱使用4根锚链进行锚定，分别系挂在如图3所示的桥节上A、B、C、D处的系锚点上。设各系锚点上锚链走向与浮箱长边夹角为α，如图3所示。α以15°为步长，在15°～165°范围内取值，α为15°～75°时的布链方式为“交叉式”，α为90°时的布链方式为“平行式”，105°～165°时的布链方式为“八字式”。浅海浮式栈桥所处浅海的水深为8.0 m，根据资料可将投锚距离定为90.0 m。

3 计算结果的比较分析

横摇在浅海浮式栈桥使用中对车辆安全通行影响最大，其次是纵摇，但不能仅按照横摇和纵摇来判定布链方式的优劣。文献[18]在单个系泊浮体布链方式的研究中指出，衡量布链方式优与劣的主要因素是锚链所能提供的横摇和艏摇恢复力矩的大小和方向。如果综合考虑艏摇和横摇，锚链是控制艏摇的主要因素，所以其恢复力矩的大小直接影响到艏摇幅值的大小；对于横摇来说，除锚链横摇恢复力矩外，还有静水恢复力矩，且对于较大尺度浮体，一般情况下锚链横摇恢复力矩远小于静水恢复力矩，所以锚链不是控制横摇的主要因素，可以不必考虑其对横摇幅值的影响[18]。除此之外，文献[19-20]都以浮体水平位移和水深的比值作为浮体允许位移的标准。

因此在波浪荷载方向为30°、风流荷载方向分别为0°、30°和90°三种情况下，计算300 s内浮箱6个自由度方向的位移平均值和4根锚链的锚链力随α变化情况，并进行比较分析。

3.1 风、流荷载方向为0°

风流荷载方向为0°时，浮箱在6个自由度方向的位移随α的变化如图4所示。

图4 风流荷载方向为0°时浮箱在6个自由度方向的位移随α的变化

由图4a)、b)可知：当α较小或较大时，即采用交叉布链或八字布链，且锚链的走向与风、流荷载方向夹角很小时，锚链对浮箱纵荡的限制作用比较明显，而对浮箱横荡难以形成有效的限制作用，只有当浮箱横荡达到一定程度时，锚链被“拉紧”后，锚链水平分力才能与外部荷载相平衡；当α=90°时，即平行布链时，锚链走向与风、流荷载方向的夹角为90°，锚链对浮箱横荡的限制作用十分明显，而对浮箱纵荡难以形成有效的限制，只有当纵荡到达一定程度，锚链水平分力方向与风、流荷载方向不再具有明显的垂直关系时，锚链才能对浮箱的纵荡产生一定的限制作用。

由图4e)可以看出:随α的增加，浮箱的横摇平均值存在着减小的趋势，但浮箱横摇的变化幅度不足0.1°。由此可见，交叉布链对浮箱横摇的限制作用比八字布链弱，但八字布链的优势并不是十分明显。

由图4f)可以看出:当α较小时，艏摇平均值较大，这主要是由于锚链走向与风、流荷载方向的夹角较小，锚链难以对浮箱艏摇形成有效的限制作用；当α=40°～70°时，浮箱的艏摇平均值的变化较小；当α=90°时，即平行布链时，浮箱艏摇平均值存在最小值；当α大于90°时，即八字布链时，艏摇平均值先随α增加而增大，后有所减小，并在145°附近存在极大值。

由图4可知，随α的增加，浮箱纵荡、横荡和艏摇平均值的变化幅度较大，浮箱垂荡、横摇和纵摇平均值的变化幅度较小。若只从对车辆安全通行影响最大的横摇平均值来判定，显然是八字布链稍具优势。但在作业条件下浮箱的水平位移也应有一定的限制，交叉布链和八字布链的纵荡平均值和横荡平均值的变化十分相似，α=40°～70°时的交叉布链艏摇平均值比α在110°～140°时的八字布链艏摇平均值小。通过比较可以看出，平行布链或α接近90°的交叉布链和八字布链不可取，而且当α较小或者较大时，也并非合适的布链方式。

风流荷载方向为0°时锚链力随α的变化如图5所示。

对于1#锚链，由于浮箱重心发生了偏向A点的位移，故α较小时，即布链方式为交叉布链时，1#锚链被“拉紧”，所以锚链力较大，且随着α的增加而增大；当α较大时，即为八字布链时，1#锚链处于“放松”的状态，故锚链力偏小。

对于2#锚链，当α较小时，即交叉布链时，与B点相连接的2#锚链处于“放松”的状态，故锚链力偏小；当α较大时，即为八字布链时，2#锚链被“拉紧”，故锚链力较大。

对于3#、4#锚链，由浮体纵荡和横荡位移的方向，虽然3#锚链力和4#锚链力出现的变化与1#锚链力和2#锚链力的变化不同，但原因是相同的。3#锚链力在α为40°～70°的交叉布链时比较小，4#锚链力在α为45°附近时有着一段较为平稳的值。

a)1#锚链 b)2#锚链 c)3#锚链 d)4#锚链图5 风流荷载方向为0°时锚链力随α的变化

由图5可以看出，3#锚链和4#锚链的受力较大，外部环境荷载主要施加于浮箱的CD边一侧。同时可以看出，当α接近90°时，锚链力平均值较大，故要尽量避免采用平行布链或α接近90°的交叉布链和八字布链。

3.2 风、流荷载方向为30°

风流荷载方向为30°时，浮箱在6个自由度方向的位移随α的变化如图6所示。

图6 风流荷载方向为30°时，浮箱在6个自由度方向的位移随α的变化

由图6可知，浮箱纵荡、横荡和艏摇随α的变化与风、流荷载方向为0°时的浮箱纵荡、横荡和艏摇随α的变化规律基本相似，故不论是选择交叉布链还是八字布链，α的值都要处于一个较为适中范围内。在横摇平均值的比较上，交叉布链在α=45°附近时，浮箱横摇方向的位移有着一个极小值，而且从浮箱艏摇方向的位移看来，α=40°～70°时的交叉布链似乎更为合适。

风流荷载方向为30°时锚链力随α的变化如图7所示。

由图7可以看出，3#锚链和4#锚链的受力比风、流荷载方向为0°时3#、4#锚链的受力更大。同时，3#锚链力在α为45°～75°时出现了变化比较平稳且数值较小的一段曲线，4#锚链力在45°附近时存在极小值。故在选定布链方式后，可由此确定一个较为具体的α值。

a)1#锚链 b)2#锚链 c)3#锚链 d)4#锚链图7 风流荷载方向为30°时锚链力随α的变化

3.3 风、流荷载方向为90°

风流荷载方向为90°时，浮箱在6个自由度方向的位移随α的变化如图8所示。

图8 风流荷载方向为90°时，浮箱在6个自由度方向的位移随α的变化

由图8可知：各方向的浮箱位移平均值随α的变化较之前两种工况下的变化趋势基本一致。浮箱纵荡、横荡随α的变化与风、流荷载方向为0°和45°时的浮箱纵荡、横荡随α的变化仍然十分相似。交叉布链时的横摇平均值虽然仍大于八字布链时的横摇平均值，但变化范围更小。在交叉布链α约为45°～75°时，浮箱的艏摇平均值比较小且存在着极小值，而在α较大时，即八字布链时，浮箱的艏摇平均值略大。

风流荷载方向为90°时锚链力随α的变化如图9所示。

a)1#锚链 b)2#锚链 c)3#锚链 d)4#锚链图9 风流荷载方向为90°时锚链力随α的变化

由图9可以看出，1#锚链力和2#锚链力随α的变化与之前两种工况下的变化规律基本相似，但变化范围明显变小，可见1#锚链和2#锚链处于 “放松”的状态。3#锚链力和4#锚链力随α的变化与之前两种工况下的变化规律有所不同，当α较小或较大时，3、4#锚链的锚链力平均值都比较大，这主要是由于锚链的走向与比风、流荷载方向的夹角接近90°，浮箱只有在出现一定的横向位移，锚链被“拉紧”后，才能产生与外部荷载相平衡的锚链水平分力。

在实际工程中，浅海浮式栈桥是由首尾相连的浮箱式桥节拼组而成，浮桥纵向两端会安装多根缆索来固定浮箱，整个栈桥的纵荡位移还会有所减小。上述分析表明：纵荡平均值和横荡平均值的变化范围较大，故α的取值应当适中为宜，不应较小或较大或接近于90°，八字布链时的横摇平均值较交叉布链时的横摇平均值略大，而纵摇和艏摇平均值的比较可以看出交叉布链较小。但布链方式的选择不仅需要考虑浮箱位移和锚链力的大小，还要考虑布链方式对施工、通航、经济性等方面的影响，考虑到通航和前方尚需要建造靠泊平台的情况，且在α的取值较为适中时交叉布链和八字布链的区别较小，故将布链方式定为交叉布链。浅海浮式栈桥的α具体值可根据浮箱六自由度位移随α的变化情况，以及锚链力随α的变化情况，将其定为45°。

4 结论

利用ANSYS下基于势流理论的高度集成模块AQWA，对浮式栈桥锚碇系统的布链方式进行计算分析，对比浮箱六自由度的位移平均值和4根锚链的锚链力平均值，表明：

1)浮箱的横荡平均值和纵荡平均值受布链方式的影响很大，在内河浮桥锚定中常用的平行式布链并不适用于浅海浮式栈桥的锚定，α较小的交叉式布链或α较大的八字布链同样不适用于浅海浮式栈桥的锚定。

2)布链方式不是控制横摇的主要因素,是控制艏摇的因素。

3)对处于迎受风、流、浪荷载一侧的3#和4#锚链而言，锚链力远比1#和2#锚链的锚链力大，而且在α为40°～60°、120°～140°的范围内时，3#和4#锚链力基本处于一个相对较小的变化范围。