改进的蒙特卡罗法漫坝风险及不确定因素研究

王之中

(抚顺市水利技术推广中心，辽宁 抚顺 113008)

水库大坝不仅可以缓解非汛期水资源短缺问题，而且能够降低下游遭受洪灾的风险，对已建大坝进行漫坝风险分析具有重要的现实意义。水库大坝作为水资源调节的建筑工程，一方面能够增强河流区域的抗洪能力，并且通过水资源供水、灌溉和发电等给社会带来经济效益；另一方面，大坝存在溃坝、漫坝等安全隐患，一旦出现问题必然导致严重后果[1]。我国洪水漫顶引发的事故时有发生，找到一种科学、有效的评估方法对漫坝风险进行分析，对于合理地利用洪水资源、减少洪水灾害和解决工程安全具有十分重要的现实意义[2]。漫坝风险分析通常与可靠性相对立，与不确定性相联系，经过长期发展，风险分析理论逐渐成为一种应用科学。Sun等采用一次二阶矩法和蒙特卡罗法对东武仕水库漫坝风险进行求解，发现一次二阶矩法计算结果均值稍微偏大[3]。Goodarzi等通过拉丁超立方抽样法对Doroudzan水库进行初始水位、洪峰流量和泄流系数的不确定性评估，发现风速和水位对漫坝风险具有显著影响[4]。李宗坤等结合水文、水力因素的不确定性建立漫坝风险模型并对各阶段漫坝风险进行分析，发现施工进度的不确定性对土石坝建设期风险具有显著影响[5]。文章通过采用重要抽样与拉丁超立方抽样结合的方法代替简单抽样法作为改进的蒙特卡罗法，根据漫坝的风险计算模型和频率分析不确定性风险计算模型对大伙房水库进行漫坝风险分析，为大伙房水库汛期迎洪提供了参考依据。

1 漫坝风险分析

1.1 改进的蒙特卡罗法

蒙特卡罗法作为一种解决不确定性问题与随机性问题的主要方法，具有通用性强和直观简单的特点，但是在其计算过程生成区间分布随机数时，一般通过简单随机抽样，导致计算效率低下，需要充足的样本点才能达到一定的精确度[6-7]。为提高计算效率，采用重要抽样与拉丁超立方抽样结合的方法代替简单抽样法，称为改进蒙特卡罗法。首先，利用重要抽样法使得样本点尽可能处于目标区域，然后根据拉丁超立方抽样对各个区域进行层次划分，减少重复抽样的概率，进而提高运算效率和抽样效率。抽出的样本变量不确定性忽略不计时，根据拉丁超立方抽样方法在每个区域中生成N个样本序列，区域中发生次数为n，则各区域发生漫坝的概率为n/N，漫坝的总体概率为：

(1)

风的影响无法忽略时，漫坝总概率计算过程分为四个步骤：①结合重要抽样与拉丁超立方抽样的方法将风与洪水构成的整体分为四个区域，并得到各自区域的随机样本。②将洪峰流量样本输入至水库调洪演算。③根据风浪引起的波浪爬高与水面壅高模型，得到水库最高水位值。假如某一年内存在漫坝模型功能函数低于0的情况，则表示该年发生了漫坝事件。④重复以上步骤，统计各个区域中漫坝事件的发生次数，进而根据式(1)计算漫坝的总概率。

1.2 漫坝的不确定性因素分析

漫坝的不确定性因素主要包括：洪水、风浪、水库面积与库容和泄水能力。洪水作为漫坝的主要风险因子，其不确定性体现为设计洪水的推求、洪水的时空分布和洪水过程线的推求三个方面。风浪的不确定性主要由风向和风速引起的。水库运行过程中，水库面积与库容随着泥沙的淤积也会发生变化，因此，库容与面积曲线通常根据正态分布的均值进行计算。水库泄水能力的不确定性来源较多，例如测量误差、闸门故障和三维水流简化为一维水流模型等。

1.3 频率分析不确定性计算

通常情况下，洪水频率分析得到洪峰流量值QT为某个确定值，忽略了洪水频率分析误差产生的不确定性，难以避免给风险分析结果带来一定的影响。假设频率分析误差服从正态分布，通过重要抽样和拉丁超立方抽样结合的方法得到T年洪峰流量gT，洪峰流量s处于95%的置信区间，其标准差为：

(2)

式中，u—均值为0的标准正态变量；σ—水文事件的标准偏差。

使用改进的蒙特卡罗法产生正态分布随机样本，样本大小为M，T年洪峰流量为样本均值，考虑频率分析不确定性的漫坝风险计算公式为：

(3)

式中，mi—考虑流量不确定性因素时各区域内漫坝的次数。

1.4 漫坝风险评估步骤

漫坝风险的评估过程主要包括以下四个步骤：①漫坝风险因子识别。水库大坝风险因子主要包括洪水与风浪。②针对风险因子进行相关数据收集，整理其分布特征，计算其设计频率值。③不确定性因子的分布特征确定以后，研究频率分析不确定性对漫坝风险计算结果的影响。④最后进行波浪爬高、水面壅高的计算和调洪演算。如图1所示。

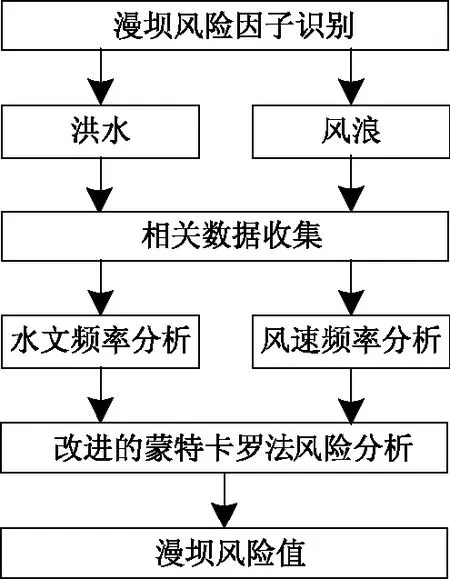
图1 漫坝风险评估流程图

2 大伙房水库漫坝风险分析

2.1 改进的蒙特卡罗法与蒙特卡罗法对比分析

图2为蒙特卡罗法风险率与模拟次数曲线，图3为改进的蒙特卡罗法风险率与模拟次数曲线。由图2与图3可知，经过足够次数迭代之后，蒙特卡罗法风险值稳定为2.769×10-6，改进的蒙特卡罗法风险值稳定为2.748×10-6，两者计算结果十分接近，但是两种方法需要的迭代次数却相差很大，蒙特卡罗法迭代次数大概为20万次，而改进的蒙特卡罗法迭代次数大概为1.5万次，计算量约为前者的7.5%。

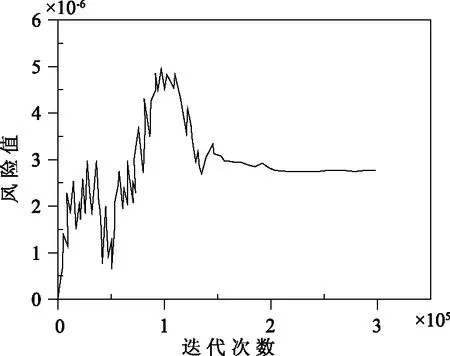
图2 蒙特卡罗法风险率与模拟次数曲线

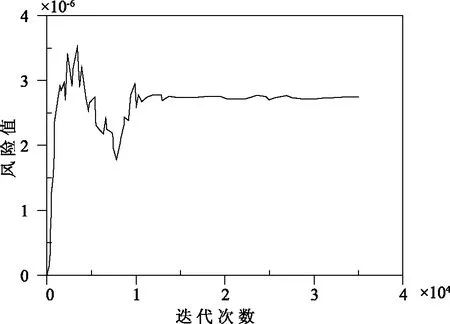
图3 改进的蒙特卡罗法风险率与模拟次数曲线

2.2 漫坝风险计算

以大伙房水库为例进行漫坝风险分析，忽略频率分析不确定性时，通过改进的蒙特卡罗法得到的10000个设计的风速与洪峰流量样本进行计算[8]。考虑频率分析不确定性时，将设计样本值作为均值，标准差由式(2)计算得到，重新生成符合正态分布的样本50个，进而样本整体变为10000×50个。大伙房水库不同起调水位的风险分析结果详见表1、表2。

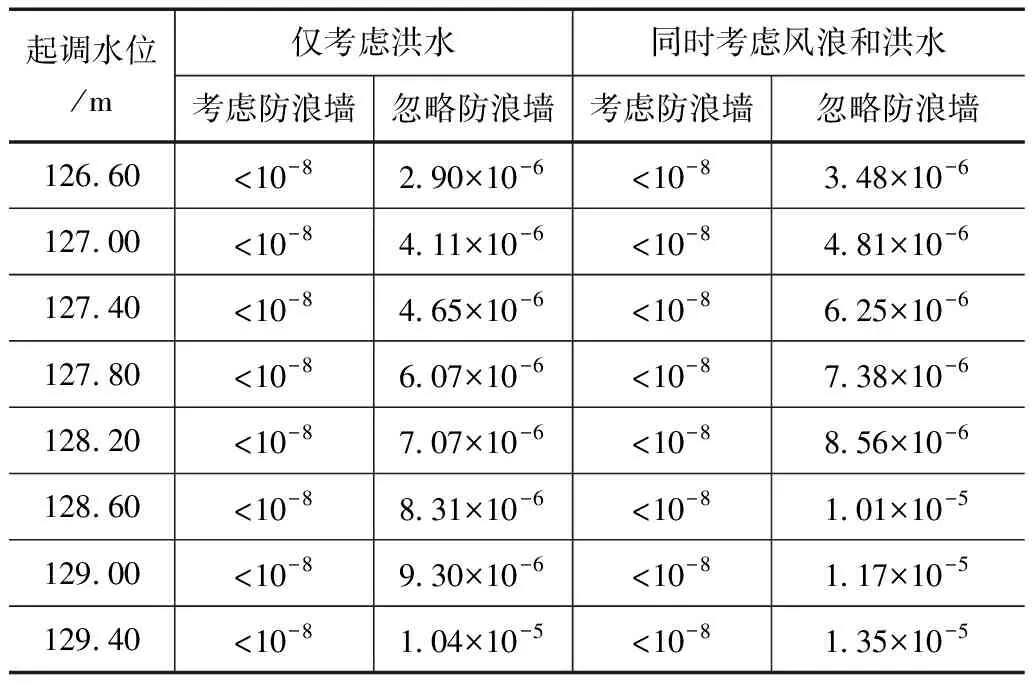
表1 忽略频率分析不确定性的大伙房水库漫坝风险

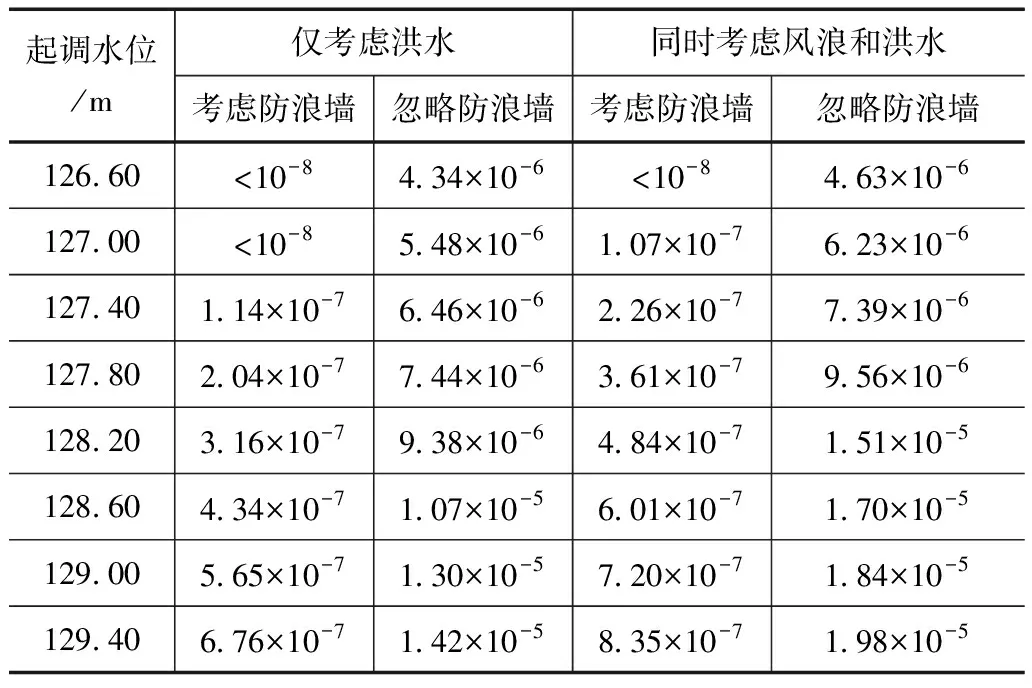
表2 考虑频率分析不确定性的大伙房水库漫坝风险

由表1与表2可以发现，风浪对于漫坝风险具有显著的影响。忽略防浪墙作用时，风浪和洪水联合作用下产生的漫坝风险是洪水单独作用产生的漫坝风险的1.06～1.63倍。因此，漫坝风险分析时，不能直接忽略风浪的作用，尤其是汛期具有强风的河流与海域，研究洪水与风速共同作用对漫坝风险的影响具有十分重要的意义。对比表1与表2可以发现，忽略防浪墙作用时，对于风浪和洪水联合作用产生的漫坝风险，考虑频率分析不确定性的计算结果是忽略频率分析不确定性的计算结果的1.22～1.42倍，对于洪水单独作用产生的漫坝风险，相应的比例为1.17～1.80倍。由此表明，频率分析不确定性能够对漫坝风险产生一定的影响，忽略频率分析不确定性的风险计算值相对偏低，据此得出的结论对水库的运行安全具有不利的影响。

借鉴国外经验，假定大伙房水库漫坝风险允许值为71200/(年×坝)，漫坝发生之后下游损失为1011数量级，则其允许漫坝风险为7.12×10-7[9]。忽略频率分析不确定性时，将126.60m作为迎洪的起调水位，考虑防浪墙的作用时，由风浪和洪水共同作用产生的漫坝风险小于允许漫坝风险；忽略防浪墙的作用时，由洪水产生的漫坝风险大于允许漫坝风险，说明由于防浪墙的存在，其漫坝风险处于允许风险范围之内。随着起调水位的不断提高，考虑防浪墙的作用，由风浪和洪水共同作用产生的漫坝风险依然低于允许漫坝风险。考虑频率分析不确定性和防浪墙作用时，大伙房水库起调水位允许提高至128.60m，此时风浪和洪水共同作用产生的漫坝风险小于允许漫坝风险。

3 结论

采用重要抽样与拉丁超立方抽样结合的方法代替简单抽样法作为改进的蒙特卡罗法，根据漫坝的风险计算模型和频率分析不确定性风险计算模型对大伙房水库进行漫坝风险分析，通过对比改进的蒙特卡罗法与蒙特卡罗法，发现两者的稳定风险值十分接近，但是改进的蒙特卡罗法的计算量是蒙特卡罗法计算量的7.5%。风浪对于漫坝风险具有显著的影响，忽略防浪墙作用时，风浪和洪水联合作用下产生的漫坝风险是洪水单独作用产生的漫坝风险的1.06～1.63倍。频率分析不确定性对漫坝风险产生一定的影响，忽略频率分析不确定性的风险计算值相对偏低，漫坝分析过程中应该关注频率分析不确定性。考虑频率分析不确定性和防浪墙作用时，大伙房水库起调水位允许提高至128.60m，风浪和洪水共同作用产生的漫坝风险小于允许漫坝风险，为大伙房水库汛期迎洪提供了参考依据。