无背索斜拉桥竖弯刚度评估模型与方法研究

蔡向阳，苏潇阳，康厚军，龚 平，刘海波，胡建华

(1.湖南省汝郴高速公路建设开发有限公司，湖南 郴州 423000;2.湖南大学 土木工程学院，长沙 410082;3.湖南省交通规划勘察设计院，长沙 410008)

无背索斜拉桥由于其优美独特的桥梁结构形式，自1992年世界上第一座无背索斜拉桥——Alamillo桥[1-2]在西班牙塞维利亚建成以来，便立即引起了桥梁工程界对这种桥型的探索与研究。在国外，George[3]研究了不同材料无背索斜拉桥在活载作用下主梁的反应；Lazar[4]研究了无背索斜拉桥的刚度问题；Robin[5]结合实际工程与美学对Zwolle桥的设计构思进行了介绍；Starossek[6]研究了无背索斜拉桥的桥塔受力。在国内，陈爱军等[7]对无背索竖琴式斜拉桥的合理结构体系进行了分析；施新欣等[8]对无背索斜拉桥进行了参数化分析，并讨论了部分参数对动力性能的影响；俞国际等[9]对钢筋混凝土独塔无背索斜拉桥的施工工艺进行了介绍；狄谨等[10]对无背索斜拉桥施工过程进行了仿真计算，给出了施工控制的各种指标。以上研究大都通过有限元软件建模进行计算[11]，至今未见到针对该类桥梁的相关理论研究，以及简便的分析评估方法。

经典传递矩阵法是20世纪20年代建立起来的用于研究弹性构件组成的一维线性系统振动问题的方法，在60—70年代的结构振动研究中广泛应用[12]。很多学者对其进行了研究，例如吉伯海等[13]将二维力学模型向弹簧支承连续梁模型转换，实现了传递矩阵法在钢斜拉桥结构计算中的应用。孙建鹏等[14]基于传递矩阵法，对曲线桥的振动特性进行了分析。Abbas等[15]应用有限元传递矩阵法研究了高温环境下变厚度壳的振动特性。近年来，Zhao等[16-17]将传递矩阵法应用于索-拱结构的动力学研究。目前，传递矩阵法已广泛应用于现代工程技术领域。

碳纤维增强复合材料(Carbon Fiber Reinforced Polymer，CFRP)由于其优越的力学性能(轻质、高强、耐腐蚀[18])，成为桥梁动力学领域的研究热点，被广泛应用于替换传统钢拉索。目前，国外已成功地采用CFRP拉索替换钢拉索[19]，东南大学RC & PC结构教育部重点实验室联合相关单位也建成了首座CFRP拉索斜拉桥[20](江苏大学人行桥)。但目前对于CFRP换索的研究还仅局限于传统直塔斜拉桥，对于无背索斜塔斜拉桥的换索研究却未见到。

本文将建立无背索斜拉桥的双梁离散弹簧力学模型，采用传递矩阵法对无背索斜拉桥在成桥状态下自由振动的特征值问题进行计算，并基于频率对其竖弯刚度进行评估，最后基于本文的理论和评估方法，对无背索斜拉桥进行CFRP换索分析。本文基本结构如下：第一部分为无背索斜塔斜拉桥力学模型，第二部分为传递矩阵法求解，第三部分为计算实例，第四部分为结论。

1 无背索斜拉桥双梁离散弹簧模型

无背索斜塔斜拉桥由于不设背索，只能利用塔柱倾斜来平衡桥面恒载和活载。在此受力体系中，斜拉索的主要作用是对桥面的弹性支承。为评估斜拉桥的整体竖弯刚度，可以忽略斜拉桥自身的局部振动。因此，本文将斜拉索简化为一无质量弹簧，其质量可以平均分配到塔和梁的连接点上进行考虑。由于其对整体刚度的影响微乎其微，因此，本文忽略其质量对整体刚度的影响。无背索斜塔斜拉桥结构可简化为如图1所示的力学模型。

为便于斜拉桥动力学分析，将桥面梁和塔视为考虑轴力影响的欧拉柏努利梁，分别记为梁1和梁2。由于无背索斜拉桥一般采用塔梁墩固结体系[21]，所以我们可以把图1进一步简化为如图2所示的双梁离散弹簧模型。

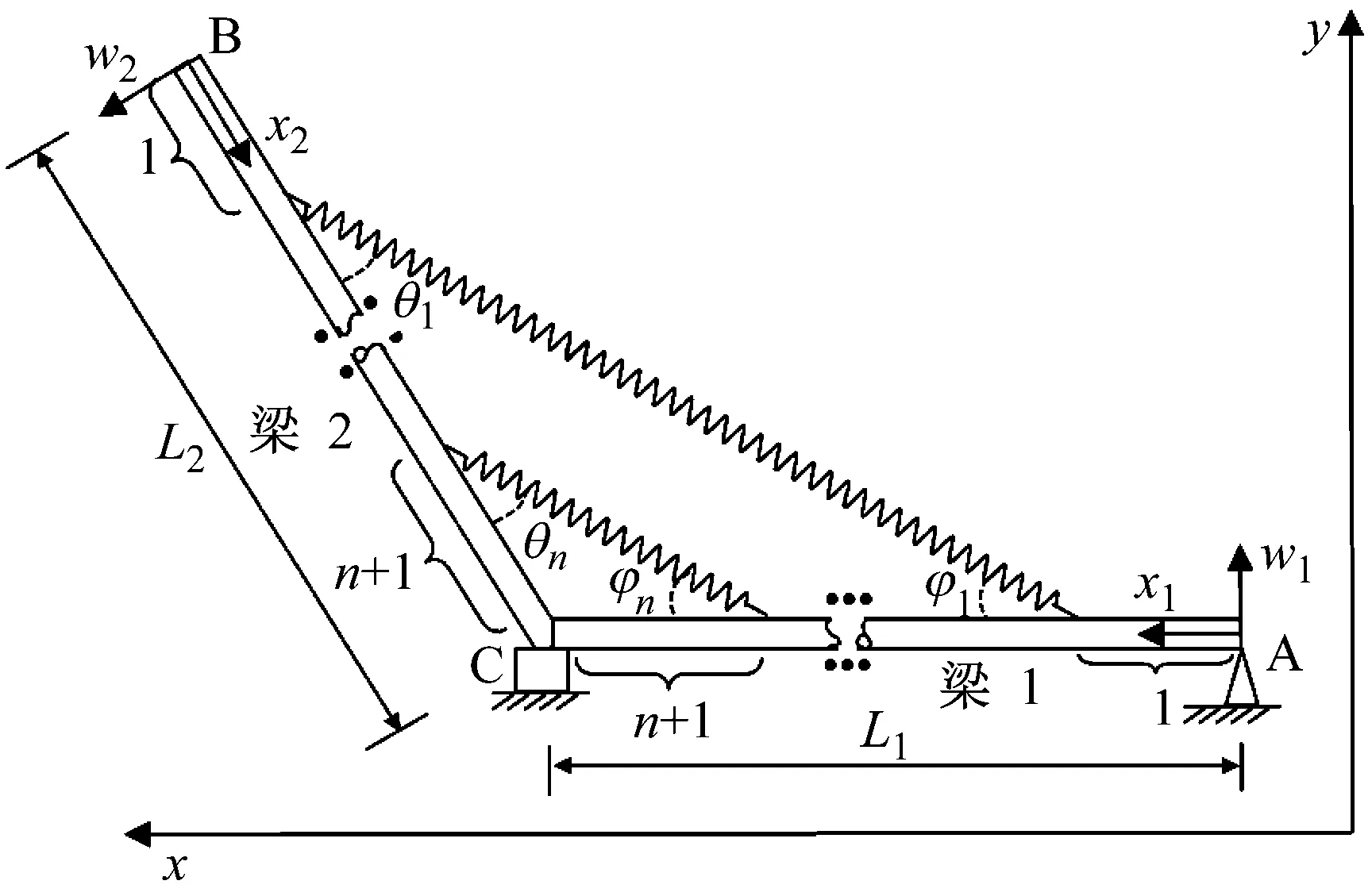
图1 无背索斜塔斜拉桥力学模型Fig.1 Mechanical model of inclined pylon of cable-stayed bridge with no backstays

图2 双梁离散弹簧模型Fig.2 The dynamic model of double beams with discrete springs

在利用上述模型进行求解之前，我们做如下基本假设：①梁和塔均为细长结构(截面高跨比小于0.1)；②不计索的垂度和质量，将拉索简化为如图1所示的无质量弹簧；③忽略塔自身重力产生的轴力影响；④只记入拉索初张力对梁轴力的影响，忽略其动应力产生的张拉力对梁轴力的影响；如图1所示，分别建立各梁的坐标系。分别用坐标x1，x2表示梁的轴向坐标，用w1，w2表示横向动位移，长度分别为L1和L2。接下来分别将两根梁根据索的数量n分成n+1段，其长度分别为l1,i，l2,i(i=1,2,3,…,n+1)，弹簧的刚度分别为ki(i=1,2,3,…,n)。

2 竖弯刚度评估的传递矩阵法

为便于应用传递矩阵法进行求解，将斜拉桥的每段梁分开并考虑为等截面梁，变截面梁可通过细化梁段加以考虑。斜拉索作用位置考虑为节点，弹簧作用通过节点条件考虑。各段梁的运动微分方程如下

(1)

式中:T0,i为梁的初始轴力;ρm,iAm,i和Em,iIm,i分别为梁单位长度的质量和梁横截面抗弯刚度。令

wi(xi,ti)=wi(xi)qi(ti)

(2)

可求得

(3)

其中

(4)

(5)

根据力和位移的关系，可求得转角、弯矩、剪力如下

θi(xi)=Di,1αicos(αixi)-Di,2αisin(αixi)+

Di,3βicosh(βixi)+Di,4βisinh(βixi)

(6)

(7)

Qi(xi)=-EiIiw‴i(xi)=

(8)

同理，将以上关系应用于斜塔，在相应的位移、转角、弯矩和剪力上方加“～”表示。力和位移的关系写成如下矩阵形式

ti=TiCi

(9)

其中，

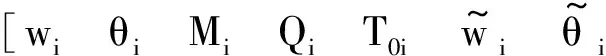
(10)

Ci=[Ci,1Ci,2Ci,3Ci,4T0iCi,5Ci,6

(11)

Ti为10×10的矩阵，如式(12)所示。

其中的一些表达式如下

si,1=sin(αixi),ci,1=cos(αixi),si,2=sinh(βixi),

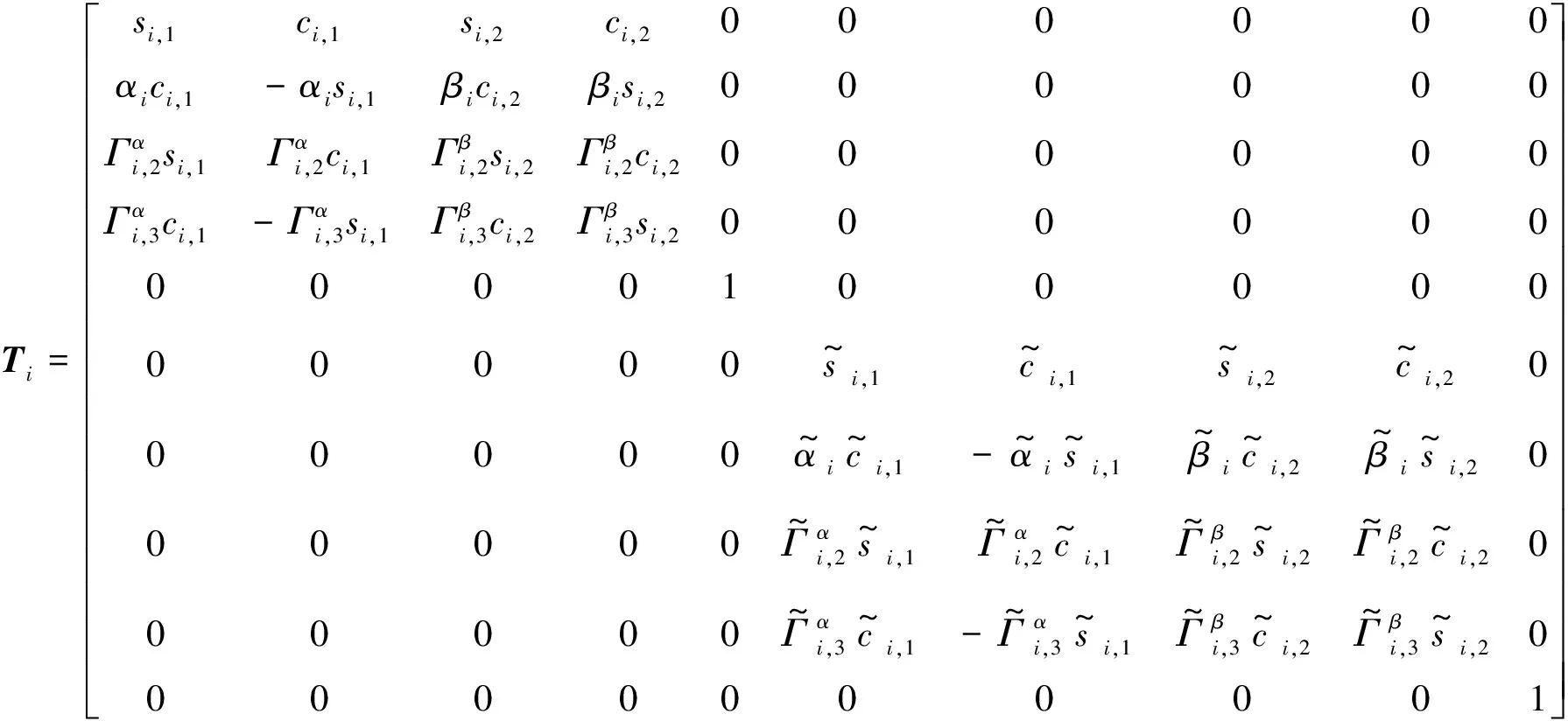
(12)

现在来求Ci，对于任意一段i,当坐标xi=0(i=1,2,3,…)时,有

(13)

所以

(14)

式中:ti和ti,0分别为第i段的末端和初始端状态向量(图 2中从左向右传递)。

现在，根据传递矩阵法原理，我们来考虑斜拉索作用点处的受力。如图3所示，设φi为索与梁的夹角，θi为索与塔的夹角，ki为索的刚度，各节点的位移、转角、轴力、弯矩和剪力有如下关系。

(15)

(16)

(17)

(18)

图3 斜拉索作用点处受力图Fig.3 Internal force of anchorage point of cable-stayed bridge

(19)

(20)

(21)

(22)

(23)

(24)

将式(15)～(24)写成矩阵形式

(25)

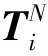
(26)

将式(14)代入式(25)中，可以得到

(27)

最后,对整个斜拉桥，有

tn+1=Tt1,0

(28)

式中，T为总传递矩阵，且有

(29)

(30)

(31)

(32)

对于式(28)，应用边界条件，可改写为

(33)

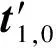
Δ=detT′=0

(34)

3 工程实例

3.1 工程概况

长沙市洪山大桥主孔跨径206 m，该桥坐落于洪山庙休闲度假区，跨浏阳河，属市内北二环关键工程，南邻机场高速，北靠长沙世界之窗，西侧比邻长沙大学,地理位置十分重要。大桥主梁采用钢-混凝土组合脊骨梁结构形式，桥面宽为33.2 m，双向六车道。索塔为预应力混凝土箱形结构，塔身水平倾角58°，桥面以上塔高138.3 m，是世界上第一座高度超百米的混凝土斜塔。全桥共13对拉索,以水平倾角25°平行布置，如图4所示，塔上索距为9.312 m，梁上索距12 m，横桥向2排，间距为6 m，其它具体参数详见文献[22]。

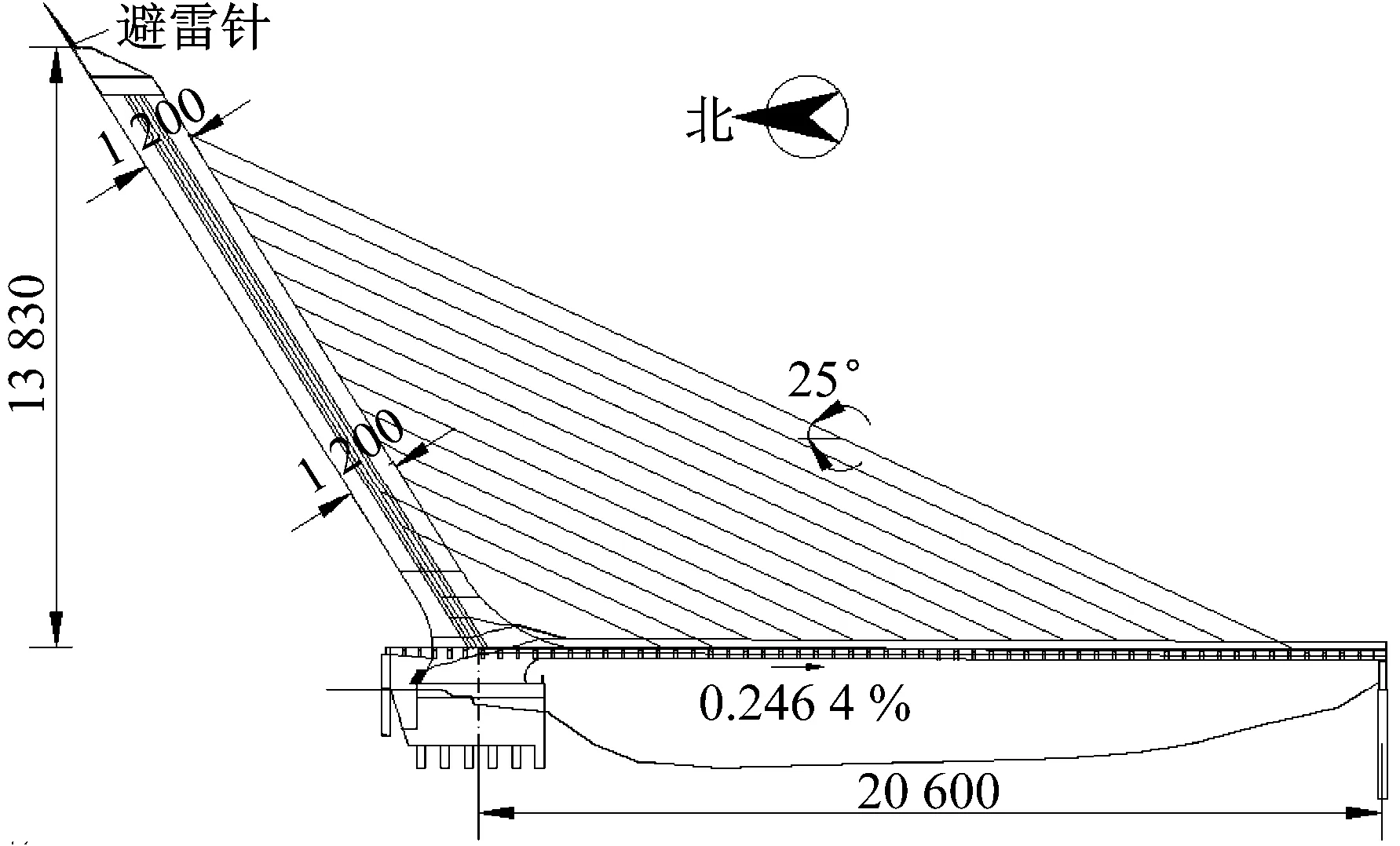
图4 洪山大桥立面图(cm)Fig.4 Elevation sketch of Hongshan bridge(cm)

3.2 计算结果对比分析

对于图4所示的无背索斜拉桥，将梁的右端视为简支，塔的上端视为自由，梁塔相交处视为固支，则

设T的各元素为ai,j(i=1,2,3…10，j=1,2,3…10)，则detT′=0可写为下式

(37)

此即为系统特征方程，由上述特征方程采用MATLAB编程即可解出斜拉桥自振频率的数值解。

接下来，为了验证本文理论的正确性，我们采用ANSYS12.0建立了无背索斜塔斜拉桥的有限元模型如图5所示，并将本文理论计算出的普通钢索斜拉桥的自振频率与有限元软件计算出的自振频率进行了对比如表1所示，由于本文忽略了斜拉索的振动，所以算出的频率都是全局模态频率(下文简称频率)。图6给出了无背索斜塔斜拉桥的前五阶模态(全局模态，下文简称模态)，这里要特别说明，采用本文理论计算出的模态，梁和塔的位移都乘以了一定的系数以便于画图，所以和ANSYS算出的模态在外观上不同，但实际上两者是相同的。从表1和图6可以看出，采用本文理论计算出的结果和ANSYS计算出的结果吻合的非常好，这不仅说明了本文理论的正确性，还为下文对CFRP斜拉索换索研究提供了理论基础。

图5 无背索斜塔斜拉桥有限元模型Fig.5 Finite element model of inclined pylon of cable-stayed bridge without backstays

表1无背索斜塔斜拉桥前7阶自振频率
Tab.1Thefirst7ordersnaturalfrequenciesofinclinedpylonofcable-stayedbridgewithnobackstays

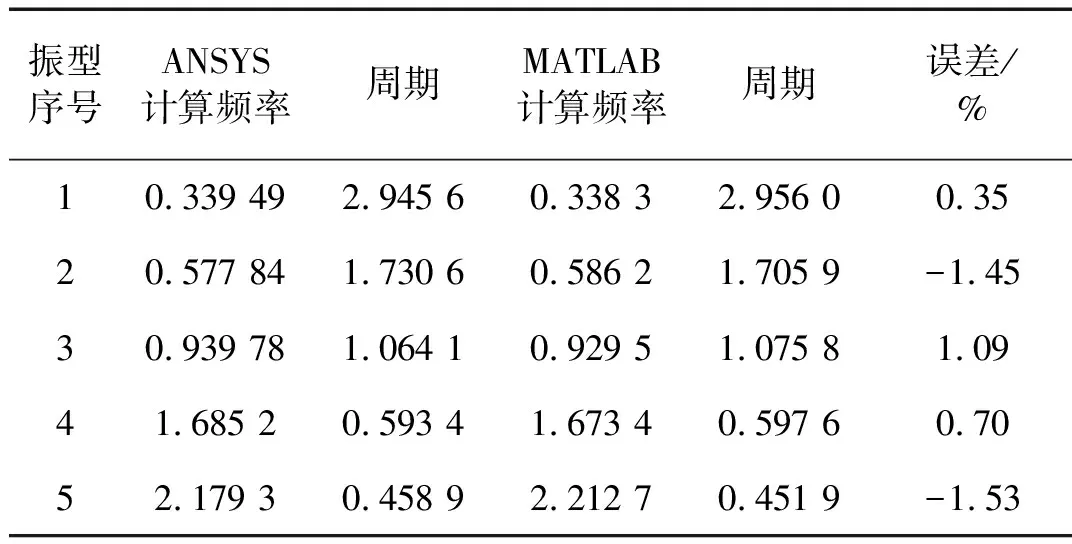
振型序号ANSYS计算频率周期MATLAB计算频率周期误差/%10.339 492.945 60.338 32.956 00.3520.577 841.730 60.586 21.705 9-1.4530.939 781.064 10.929 51.075 81.0941.685 20.593 41.673 40.597 60.7052.179 30.458 92.212 70.451 9-1.53

图7给出了CFRP索的数量和刚度对斜拉桥前三阶频率的影响。这里要特别说明，图中横坐标表示图5中的无背索斜拉桥从右至左(即从长索至短索)将普通钢索换为CFRP索的数量，纵坐标表示各阶自振频率相对于表1中对应自振频率的增量百分比。从图中可以发现，频率增量都是正的，随着CFRP索数量的增加，桥梁整体刚度呈上升的趋势，而且每阶模态下各条曲线的变化趋势相同。第二阶模态对换索的敏感性明显高于其他两阶，频率增量最大达到了60%，约为第一阶的8倍，第三阶的2倍。另外，我们可以看出：第2～4根索对第一阶自振频率没影响，第6～8根索对第三阶自振频率没影响，这说明在换索时，部分斜拉索的更换将对整体刚度有非常大的影响。而出现这种现象的原因，可能原因是这些索处于边界附近该梁本身刚度较大，使索对整体刚度的贡献相对降低。为此，我们对只换一根CFRP斜拉索时斜拉桥的整体竖弯刚度的变化规律进行了研究。

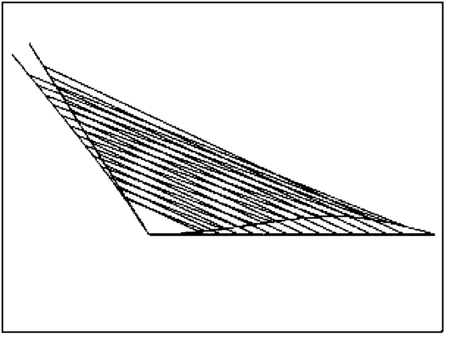
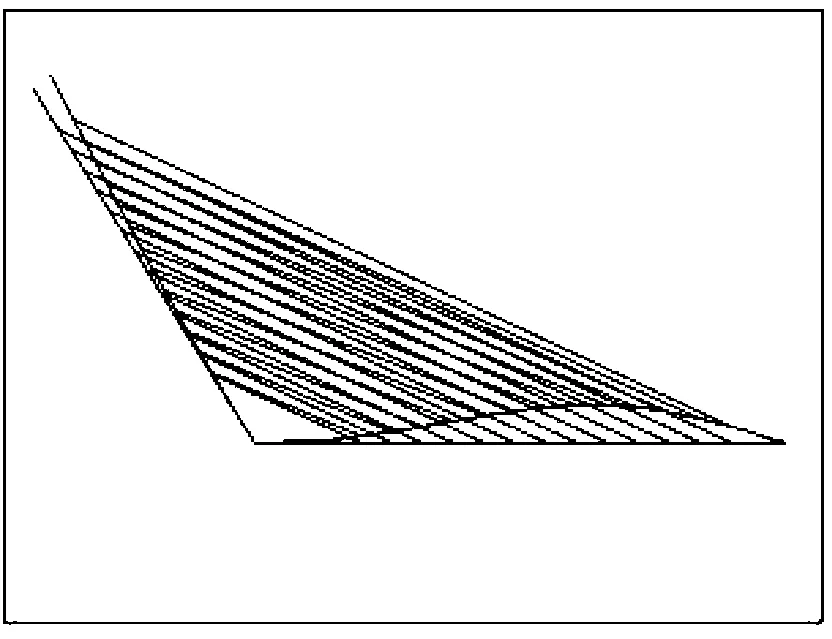
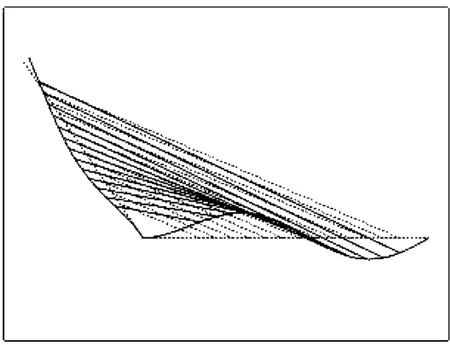
图6 无背索斜塔斜拉桥前五阶振型Fig.6 The first 5 mode shapes of inclined pylon of cable-stayed bridge without backstays

图7 CFRP索数量和刚度的变化对斜拉桥前三阶频率的影响
Fig.7 The influence of number and stiffness of CFRP cable on the first three order frequencies of cable-stayed bridge

图8给出了只更换一根CFRP斜拉索时频率的变化情况，图中横坐标表示CFRP索所处的位置(按图5中的无背索斜拉桥从右向左行进)，纵坐标同图7。从图中可以看出，各阶模态下每条曲线的变化趋势相同，当第3～4根索被换为CFRP索时，第一阶频率增量基本无变化，第6～7根索被换为CFRP索时，第三阶频率增量基本无变化，这与图7得到的结论相一致。这说明当斜拉索的位置确定了，它对无背索斜拉桥的自振频率是否会产生影响也就确定了。换句话说，斜拉索的位置决定了它对整体刚度产生多大的贡献，从而为实际工程中换索提供了理论参考。

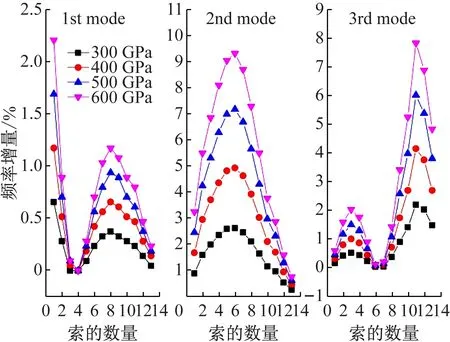
图8 CFRP索数量和刚度的变化对斜拉桥前三阶频率的影响
Fig.8 The influence of number and stiffness of CFRP cable on the first three order frequencies of cable-stayed bridge

换索时可以从左至右换，也可以从右至左换，为了考察换索的顺序对无背索斜拉桥整体刚度的影响，我们改变了换索的顺序并给出了相应的结果，如图9所示。图中横坐标表示图5中的无背索斜拉桥从左至右将普通钢索换为CFRP索的数量，纵坐标同图7。从图中可以看出，各阶模态下自振频率的变化趋势相同，随着换索数量的增加，频率在变大。第二阶频率对换索的敏感性同样高于其余两阶，最高达到了60%，约为第一阶的8倍，第三阶的2倍。另外，当第8～10根索被换为CFRP斜拉索时，第一阶频率不发生变化，当第7～9根索被换为CFRP斜拉索时，第三阶频率不发生变化。这些现象都与图7和图8中得到的结论基本一致，这说明在换索时，斜拉索的位置才是决定它对桥梁整体刚度是否产生影响的关键，换索的顺序并不会影响斜拉桥的自振频率的变化。这是因为自振频率是结构的固有属性，只与刚度和质量有关。因此，实际工程中进行换索时，工程师可以根据不同的情况选择合理的顺序进行索的更换，从而实现施工过程的合理化，提高工作效率。

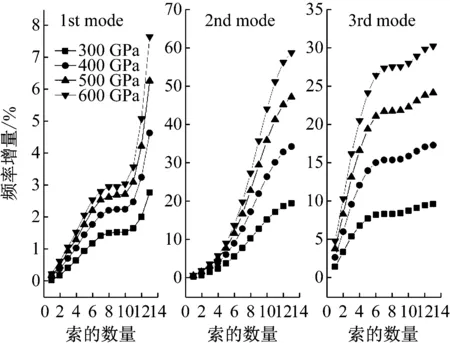
图9 CFRP索数量和刚度的变化对斜拉桥前三阶频率的影响
Fig.9 The influence of number and stiffness of CFRP cable on the first three order frequencies of cable-stayed bridge

图10给出了无背索斜拉桥自振频率随弹性模量的变化曲线图。我们可以从图中发现，当弹性模量较小时，第一阶频率有稍微的增加，当弹性模量增加到一定值时，第一阶频率基本保持不变。第二阶到第五阶频率则随着弹性模量的增加呈现出上升的趋势。另外，第一阶和第二阶频率随着弹性模量的变化出现靠近后又分离的现象，如图中A点所示，但并非两条频率变化曲线交叉，而是发生了转向(Veering现象)。这个时候两阶振型会发生快速而且连续的交换，并且两个模态之间在非线性振动时，可能产生能量传递，很容易发生内共振现象[23]。在无背索斜拉桥的设计和换索中都应该引起重视。这对指导无背索斜拉桥的设计，尤其是动力性能的控制具有重要的指导意义。

图10 CFRP索弹性模量对斜拉桥前五阶频率的影响Fig.10 The influence of elastic modulus of CFRP cable on the first five order frequencies of cable-stayed bridge

为了研究CFRP索轴力对斜拉桥自振频率的影响，我们给出了图11。从图中可以看出，随着斜拉索索力的增加，无背索斜拉桥全局模态频率基本保持不变。事实上，梁和塔振动的全局模态频率几乎不受索力的影响，反而索单独振动的局部频率受索力的影响很大，这说明在评估整体刚度时，可以忽略斜拉索索力的影响。另外，随着索力的增加，自振频率总体呈现下降的趋势，这是因为索力的增加使得梁和塔所受的轴向压力增加，从而使得梁和塔的几何刚度增加，这就导致了整个大桥的整体刚度减小，所以频率也会变小。

图11 CFRP索轴力对斜拉桥前五阶频率的影响Fig.11 The influence of axial force of CFRP cable on the first five order frequencies of cable-stayed bridge

4 结 论

本文将无背索斜塔斜拉桥的立式结构转变为链式体系，建立了无背索斜塔斜拉桥的双梁离散弹簧模型。基于传递矩阵法计算了无背索斜塔斜拉桥的自振频率和模态并对其竖弯刚度进行了评估。然后针对无背索斜塔斜拉桥的CFRP换索问题进行了详细的参数化分析和研究，从而得出了一些有意义的结论。

(1)本文建立的无背索斜塔斜拉桥双梁离散弹簧模型，简单易懂，便于采用传递矩阵法求解和编程化分析，能很好地评估无背索斜塔斜拉桥的竖弯刚度。

(2)换索时，不同位置的斜拉索对无背索斜塔斜拉桥整体刚度的影响不同，亦即斜拉索的位置决定了它对无背索斜塔斜拉桥的整体刚度产生多大的影响。从动力学的角度看，换索时只需要更换部分斜拉索就可提高结构的整体刚度。

(3)无背索斜塔斜拉桥的换索顺序并不会改变斜拉索对斜拉桥整体刚度的影响，无论是从左至右换还是从右至左换，频率增量的曲线变化趋势大致是一样的。所以，工程实际中，工程师可以根据不同的情况采用合理的换索顺序进行索的更换，提高施工效率。

(4)无背索斜塔斜拉桥的自振频率几乎不受斜拉索索力的影响。随着索力的增加，自振频率总体表现出减小的趋势，但这种减小量很小，可以忽略。然而，无背索斜塔斜拉桥的自振频率表现出对斜拉索弹性模量的敏感性，可能会出现频率变化曲线转向(Veering现象)，从而可能使结构发生内共振现象，对桥梁结构造成破坏。因此设计桥梁时应注意控制参数以防止此现象的发生。