基于WT-SVD的语音信号双层滤波方法

沈红红，何利力

(浙江理工大学 信息学院，浙江 杭州 310018)

0 引言

近年来，由于语音信号处理技术取得显著的成果，促进了语音识别、计算机听觉以及语音增强等技术研发，推动了智能家居、消费电子产品、通信以及智能汽车等领域的发展，而语言之间的相互转换成为了目前语音信号方面的研究热点。但是语音信号具有多样性和复杂性，尤其是语音信号的质量方面。要想准确地获取语音特征词，就必须去除语音信号中的噪音成分。所以，为了能够消除噪音对语音信号质量的影响，很多学者进行了相关的研究。如唐铭卓[1]提出了一种带分解的分数傅里叶变换语音去噪法，利用分数阶域的最佳滤波算子和最佳变换阶实现语音和噪声的分离。基于傅里叶变换去噪法，在提高信噪比和空间分辨率上存在相互矛盾，且去噪效果不佳。在此基础上，研究者张晓宁[2]提出了采用小波阈值去噪法，利用小波变换的多分辨率特性，有效地去除了信号噪声。鉴于小波变换对非线性时变随机信号的处理效果差，研究者郭会芹[3]提出了一种Hilbert-Huang的语音信号去噪算法；该算法具有的多分辨率和高度自适应的特性，能够很好地处理非平稳、非线性的时变随机信号。为了避免语音信号去噪后失真，研究者黄珊[4]提出了一种稀疏编码去噪方法。以上这些研究方法都在不同程度进行了语音信号去噪。

本文结合小波去噪和奇异值分解去噪研究方法的优缺点，提出了一种新的WT-SVD去噪方法，利用一段加噪的语音信号进行实验，仿真结果表明该方法有效地去除了语音信号噪音，提高了信号分辨率。

1 小波阈值去噪原理

1.1 小波变换原理

语音信号在不同场景中含有的噪音大小也不一样，为了适用于不同场合的信号去噪，通过调节小波阈值函数，确定最佳阈值，从而达到更好的去噪效果。设f(t)为有限能量的语音信号，连续小波变换[5]定义式为：

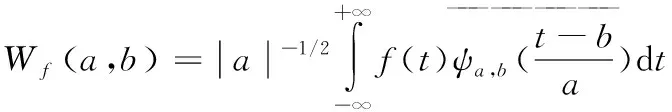
(1)

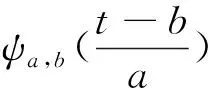
在连续小波变换中，参数a，b是连续的。但是，在实际语音信号处理过程中，为了减小计算误差，避免信号的失真，对连续小波变换进行离散化处理，即a，b参数离散化，得到离散型小波变换(DWT)[6]。DWT处理过程，首先将原始语音信号分解为近似系数和细节系数，近似系数中包含主要语音信息，然后对信号中的低频成分继续分解，反复该过程。

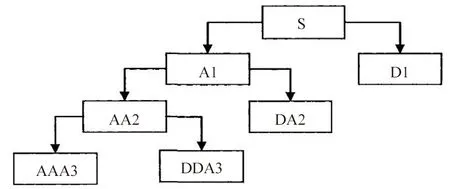
图1 三层小波分解过程

与傅里叶变换不同，小波变换将原始信号转换到频域范围，同时，也将一维的时域信号转换到二维“时间-尺度”空间上，所以f(t)的小波变换具有多分辨率特性。通过改变参数a和b可以得到一个小波序列以达到对f(t)在任意一个位置的匹配。

1.2 阈值去噪原理

小波去嗓[7]是通过对信号进行一定尺度分解后得到其在当前尺度的系数向量W，然后通过所选择的阈值量化处理函数对此小波系数向量进行处理得到Wδ，并由此重构出去噪后的估计信号。其中小波阈值去噪包括硬阈值去噪和软阈值去噪[8]，其阈值函数分别如式(2)、式(3)所示：

(2)

(3)

从软硬阈值函数可以看出，若小波系数W的绝对值小于阈值δ时，则为噪声，并将其置0。若所得小波系数W大于阈值δ，则保留该信号并对其进行处理。原始信号所包含的语音信号信息主要存在于部分小波系数上，而噪声信号所包含的信息量较少，所以与噪声成分相应的小波系数会远小于主要信号。小波阈值去噪的步骤如下：

① 选择小波基函数并确定小波分解尺度得到当前尺度下的小波分解系数向量W；

② 对各小波系数进行阈值的量化处理得到估计的小波系数向量Wδ；

③ 基于Wδ重构出去噪信号。

小波去嗓过程中，阈值函数[9]的选择和阈值的确定是小波系数向量的阈值量化处理过程中最重要的环节。阈值的确定需要根据具体的语音信号所处的环境而定，当阈值太大，则会出现信号溢出现象，即过滤掉非噪音信号。若阈值选取太小，则去噪效果差。其中小波阈值确定的4种方式如下：

② 无偏风险软阈值估计(rigrsure)：得到给定阈值m的似然估计，并最小化似然函数，就可以获得对应阈值；

③ 最小极大方差阈值(minimaxi)：此方法选取的阈值也是固定的，其计算公式为：

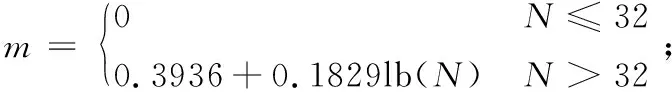
(4)

④ 选择启发式阈值(heursure)：此阈值确定方式是sqtwolog和 rigrsure阈值确定方式的综合，因为根据rigrsure所确定的阈值在信噪比比较高的情况下表现一般，heursure采用了一种启发函数选择sqtwolog和rigrsure中较好的阈值作为最终阈值。综合考虑，本文选择综合sqtwolog和rigrsure的阈值选取规则的优点的heursure方法。

1.3 改进阈值函数

软硬阈值量化处理函数存在缺陷，如图2所示，采用硬阈值函数去噪时，则所得Wδ存在间断点。当小波系数进行信号重构时会导致去噪后的信号出现振荡，造成重构信号失真。采用软阈值函数去噪时，则大于阈值的那部分ωjk会发生偏移，即与原来的值相比出现误差，这对于重构信号与原始信号的近似程度影响较大。

图2 软硬阈值函数对比

针对以上2种阈值函数的缺陷，引入了一种新阈值函数[10]，通过在硬阈值函数的基础上增加一个指数型的修正系数，函数在原间断点附近导数极大，且函数连续，尽可能减少小波系数的偏差，其表达式如下：

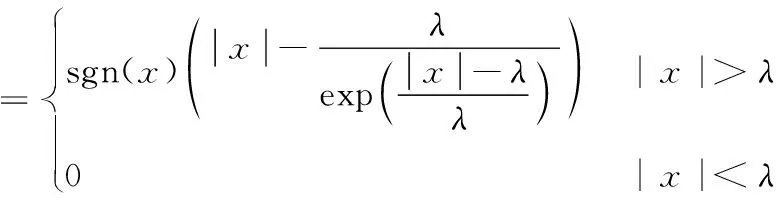
(5)

式中，λ为阈值，x为小波系数，ηx,λ为处理后的小波系数。其阈值函数如图3所示，可以看到，当x的绝对值小于λ时，同样将其全部置为0，避免去噪效果不佳，当x逐渐接近λ时，函数的收敛速度加快，使原本硬阈值量化处理函数当中的间断点消失，这样就解决了硬阈值函数会导致重构信号存在震荡的问题。当阈值函数远离λ时，此函数对x的处理较为平缓，当距离远到一定程度时则不再存在偏差，这样就尽量克服了软阈值量化处理函数对x造成的固定偏移。

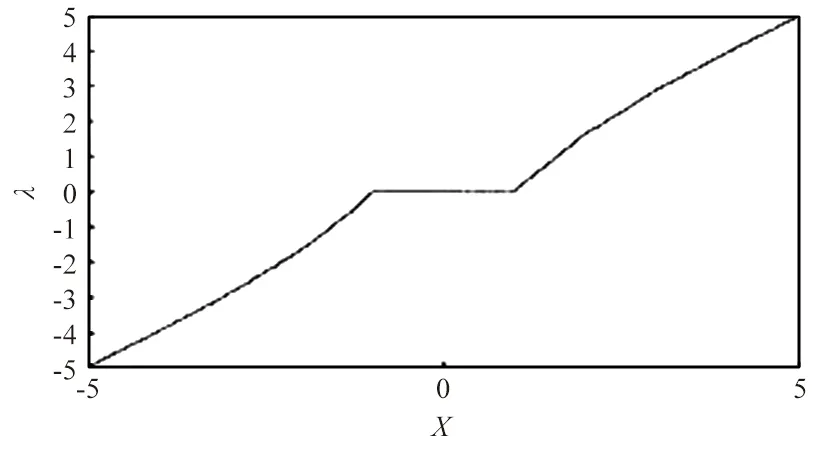
图3 新阈值函数

2 基于奇异值分解的信号去噪原理

2.1 奇异值分解去噪原理

奇异值分解[11](SVD)是一种非线性滤波，SVD降噪[12]主要依据信号量与重构矩阵奇异值之间的对应关系，将包含语音信号的矩阵分解到一系列奇异值和奇异值矢量对应的时频子空间中。一般而言，较大的奇异值会对应信息量大的信号分量，较小的奇异值对应信息量小的分量；当有用信号未被噪声淹没时，噪声信号分量对应的奇异值数值较小，只会淹没掉原信号中信息量小的分量。所以通过适当地舍弃小奇异值对应的信号分量，用大奇异值进行信号还原，则可以达到既消除噪声的影响，又保留原始信号的主要信息，得到了对原信号较好的估计，从而得到降噪信号[13]。

设有矩阵E，且存在i×i的正交矩阵C，j×j的正交矩阵U以及i×j的Σ矩阵；Σ矩阵上主对角线上的元素都为奇异值(δ1≥δ2≥…≥δr)，其余元素为零。则矩阵E的SVD为：E=CΣUT。

矩阵E的秩为r，r与非零奇异值的个数相等，则‖EQ‖可表示为：

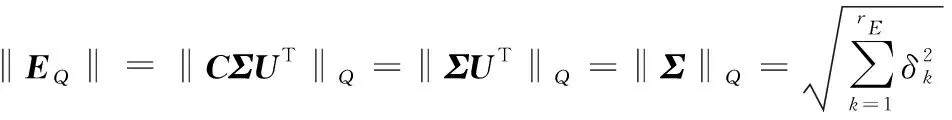
(6)

式中，矩阵C的前rE列是以矩E的列向量为基础的，而UT的前rE行是以矩阵E的行向量为基础的。为了得到一个和矩阵E相似的矩阵Em，m≤rE，令矩阵E中除了m个最大的奇异值之外的其他奇异值为零。由Brain提出的奇异值分解理论认为，可以通过最小化近似矩阵Em来确定原始矩阵E和近似矩阵之间的距离：

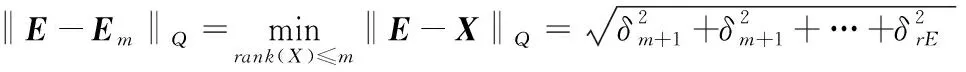
(7)

将经过小波滤波后的语音信号进行SVD二次降噪处理，奇异值分解降噪过程如下：

① 利用语音信号X=(x(1),x(2),…x(N))构造矩阵E；

② 对矩阵E进行奇异值分解，得到C∈Ri×i，Σ∈Ri×j以及U∈Rj×j，则E=CΣUT；

③ 选取奇异值阈值，然后对奇异值矩阵Σ进行处理，将小于奇异值阈值的奇异值置零，处理后的矩阵为Σ-；

④ 利用矩阵C、U和Σ-重构矩阵E-，E-∈Ri×j，则E-=CΣ-UT；

⑤ 由矩阵E-第1行的所有元素和第2行第i列至第j行第i列的j-1个元素，构造新的数据序列X-，表达式如下：

X-=[x1,1:ix(2:j,i)T]。

2.2 奇异值个数的确定

尽管奇异值分解具有简化数据、减少噪音的优点，但在信号去噪的过程中也存在奇异值选取难的问题。选择合适的奇异值个数进行信号重构，信号去噪效果好。如果选择的奇异值个数过多，则去噪后的信号中会仍然会有大量噪音存在，去噪效果差；如果选择奇异值个数表示过少，则会破坏原始信号，导致信号失真。为了解决奇异值个数选择问题，研究者给出了不同的解决方案。例如：① 利用差分谱的方法自动划分出奇异值个数；② 利用特征均值的方法，通过奇异值的特征值均值判定奇异值个数；③ 利用奇异值中值法判定个数。这些方法在一定程度上解决了奇异值个数选取问题，但是仍然存在很多缺陷。对此本文采用奇异值方差法解决该问题。

奇异值方差法：将含噪信号的矩阵经过奇异值分解后，得到奇异值δ1,δ2,…,δr)，则：

δs=varδ1,δ2,…,δr)，

式中，δs为奇异值方差，var为MATALB中求方差的运算命令。

根据奇异值的方差值来判定奇异值的个数，当判定的奇异值小于方差值时，将其奇异值置为零；当大于方差时，则保留该奇异值，作为重构矩阵的元素，实现信号降噪。

3 仿真结果分析

为了检测WT-SVD去噪方法的有效性，本文选择MATALAB进行语音信号的仿真，选择如图4所示的一段加噪的语音信号，首先进行WT滤波，如图5所示，然后将经过WT滤波的语音信号进行SVD滤波，如图6所示。

由图4可以看出，该语音信号受噪音的影响比较大，然后对该语音信号进行WT滤波；由图5可以看出，大部分的噪音都被过滤掉，但是仍然存在某些噪音未被过滤。然后对图6语音信号继续进行SVD滤波，由图6可以看出该语音信号去噪效果明显，几乎没有明显的噪音信号，且和原始信号相比，去噪后的语音信号未出现失真情况。

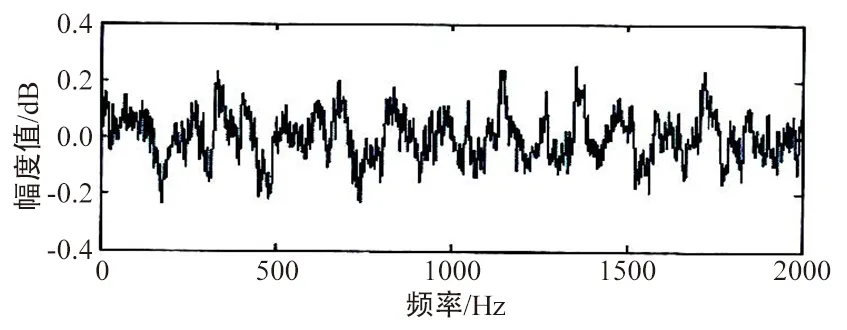
图4 原始加噪信号

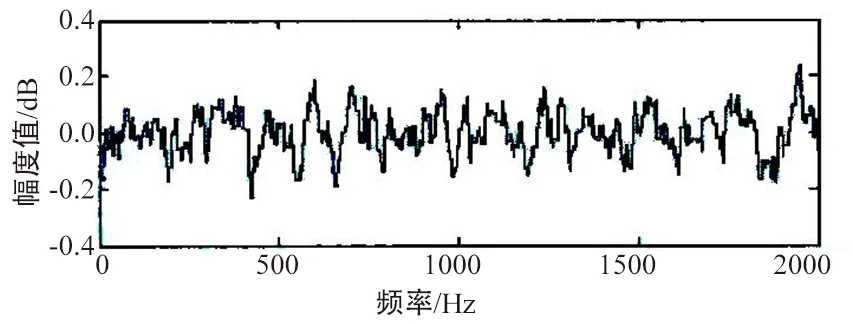
图5 WT去噪信号

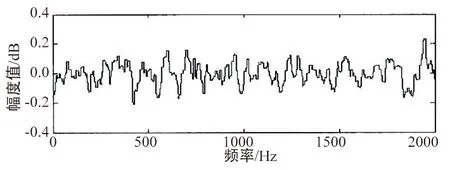
图6 WT-SVD去噪信号

4 结束语

总结了语音信号的去噪方法，研究了语音信号去噪方法中的改进问题。介绍了小波阈值去噪中的缺点，为了能够确定最优阈值函数，引入了一种新的阈值函数。克服了传统软硬值函数的缺点，缩小了小波系数固有偏差。过滤掉语音信号中的部分噪音后，利用奇异值分解滤波，过滤掉剩余的语音信号噪音。通过对语音信号进行仿真，结果表明，经过双层滤波后，极大地消除了语音信号中的噪音。在后续工作中，考虑语音信号所处环境不同，噪音大小也不同问题，将继续研究消除噪音课题。