基于检查点场景信息的软件行为可信预测模型

田俊峰，郭玉慧



基于检查点场景信息的软件行为可信预测模型

田俊峰1,2，郭玉慧1,2

（1. 河北大学网络空间安全与计算机学院，河北 保定 071002；2. 河北省高可信信息系统重点实验室，河北 保定 071002）

为了保证软件可信性，通过动态监测软件行为，对软件在一段时间内运行的可信状态进行评估，提出了一种基于检查点场景信息的软件行为可信预测模型CBSI-TM。该模型通过在软件运行轨迹中设置若干检查点，并引入相邻检查点时间增量和CPU利用率变化量定义场景信息，用以反映相邻检查点场景信息的关系，然后利用径向基函数（RBF, radial basis function）神经网络分类器评估当前检查点的状态来判断软件的可信情况，并运用半加权马尔可夫模型预测下一个检查点的状态，达到对软件未来运行趋势的可信情况的评估。实验结果证明了CBSI-TM模型能够有效地预测软件未来运行趋势的可信情况，并验证了该模型具有更优的合理性和有效性。

软件可信性；检查点；RBF神经网络；半加权马尔可夫模型

1 引言

软件可信一直是人们普遍关注的问题。软件可信是指软件系统能够按照其设定目标所预期的方式运行，软件行为和用户的预期相一致[1]。由于软件本身的设计缺陷或软件运行环境的变化可能导致软件运行故障，从而偏离预期行为轨迹，最终给人们的工作和生活带来不良影响甚至造成巨大损失。因此，研究软件行为的可信性具有重要意义。

当前对软件行为的可信研究已有不少成果。李珍等[2]采取伴随式分布软件监控机制，在节点内置入检查点，引入适合复杂交互场景的交互关联方法，提出了检查点可信性及检查点之间结构可信性的评估方法。刘玉玲等[3]提出一种基于软件行为的检查点风险评估信任模型，通过累积多个有疑似风险的检查点，运用风险评估策略，判定有疑似不可信的检查点，利用处罚或奖励机制求出软件行为的可信度，最终判别软件行为是否可信。吴佳等[4]提出了一种基于隐马尔可夫模型的软件系统状态预测方法，该方法通过收集系统的外在特征信息，利用隐马尔可夫模型建立系统内部状态与外部特征之间的联系，实时了解并预测系统状态。Guo等[5]提出了一个新的统一框架来表示硬件基础设施和软件程序，在统一框架的支持下，系统设计者/集成商将能够从不可信的第三方供应商正式验证与硬件和软件集成的计算机系统的可信性。王德鑫等[6]根据从软件开发过程的实体、行为以及制品3个方面获取的可信证据，提出了由37个可信规则、182个过程可信证据和108个制品可信证据组成的软件过程可信度模型，并给出了基于该模型证据的软件过程可信评价方法。贾晓辉等[7]提出了软件质量模型及分级的可信软件评估模型，将软件的信任程度分为6个可信级别，基于决策树给出了可信软件等级的评价过程，并将其运用在可信构件平台中。王犇等[8]提出了一种基于多属性熵权合成的软件可信等级评估方法，该方法重点解决了软件可信性评估中可信证据合成时证据冲突、多属性权重分配等问题，从而使软件可信评估的结果更加准确和真实。Li等[9]提出了一个可靠性评估模型，着重分析了软件可靠性的不同组成部分的影响，利用复杂网络理论中最有影响力的节点发现算法来计算每个组件的影响因素，根据影响因素对软件系统的可靠性进行了评估。Okamura等[10]提出了一个开放源码软件可靠性评估的统一建模框架，结合经典的非齐次泊松过程的软件可靠性增长模型（SRGM, software reliability growth model）与一个熟悉的回归方案——广义线性模型（GLM, generalized linear model），发展了一种新的框架，不仅可以估计软件的可靠性，还可以研究软件度量对故障检测过程的影响。Liu等[11]构建了基于神经网络的软件可靠性的评价指标体系，并最终实现了软件可靠性评估系统。这些研究大多是通过分析软件行为来评估当前软件系统的可信性，而通过针对软件当前运行节点可信情况来预测下一个节点的行为可信性，即对软件未来的运行趋势进行评估的研究相对较少。

因此，本文提出了一种基于检查点场景信息的软件行为可信预测模型，该模型的主要贡献如下。

1) 将获取的检查点场景信息输入训练好的RBF神经网络，对当前检查点处的软件行为进行可信性评估。

2) 在检查点场景信息中，引入了时间增量和CPU利用率变化量，反映相邻检查点之间的系统状态变化情况。

3) 结合当前检查点的场景信息和RBF对其可信性的评估结果，进一步运用改进的半加权马尔可夫模型预测下一个检查点的可信情况。

4) 实验结果表明，该模型可以针对性地预测软件未来运行趋势的可信性，便于及时管理软件行为，加强软件的可信性。

2 软件行为可信预测模型

2.1 相关定义

定义1 检查点（check point）。软件流程上的一些关键点，一般选取软件独立功能结束处和软件分支处或比较重要的系统调用处作为检查点，用以提取软件的场景信息。

定义3 行为轨迹。由软件的运行轨迹和功能轨迹组成，是指软件主体所实施的行为按照时间顺序记录下来形成的形式化序列。

定义4 运行轨迹。是指按执行顺序将检查点串联起来的序列。

定义5 功能轨迹。与运行轨迹相对应的检查点场景信息序列。

定义9 软件行为监测。是指软件运行时，在检查点处对行为信息进行收集、评估等操作，一般通过监测（软件）进行。

2.2 场景信息的选择

检查点的可信评估依赖于检查点的行为信息。根据在软件运行时监测到的检查点场景信息来分析检查点行为的可信情况，当检查点行为发生异常时，场景中的很多属性信息会发生变化。吴佳等[4]选择了变化比较直观的CPU利用率、内存占用率和磁盘利用率等作为WebLogic服务器的系统特征。根据文献[4]的研究，CBSI-TM模型选择了检查点时间、CPU利用率、内存利用率、网络传输速度，同时为了研究相邻检查点之间发生的系统状态变化，即通过软件当前检查点的状态进而预测下一个检查点的状态，CBSI-TM模型还选择了相邻检查点时间增量Δ、CPU利用率变化量Δ，最终将以上6个影响因素作为检查点的场景信息。

因此，选择以上这6个影响因素既能够反映当前检查点的系统状态，又能够反映相邻检查点的系统状态变化。

2.3 相关方法的介绍

2.3.1 RBF神经网络

RBF神经网络[12]是一个具有单隐含层的3层前馈网络，具有非线性逼近能力强、网络结构简单、学习速度快、不易陷入局部极小点和顽健性能好等优点，利用RBF神经网络有助于对大量、复杂的信息进行科学的分类。RBF神经网络结构如图1所示，包括输入层、隐含层和输出层。输入层节点只传递输入信息到隐含层，隐含层节点对输入信号在局部产生响应，输出层节点通常是简单的线性函数。

2.3.2 马尔可夫模型

马尔可夫过程[13]是研究某一事件的状态及状态之间转移规律的随机过程理论，它通过分析某一时刻不同状态的初始概率及状态之间转移概率的关系来研究未来某时刻状态的变化趋势。

图1 RBF神经网络

马尔可夫链预测的理论基础是马尔可夫过程，对其运动变化的分析主要是研究链内有限马尔可夫过程的状态及其相互关系，进而预测链的未来状况，并据此做出决策。马尔可夫模型可表示为

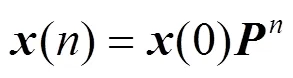
其中，()为时刻的状态概率向量，(0)为初始时刻的状态概率向量，为状态转移概率矩阵。

由2.2节的分析可知，影响检查点状态变化的场景信息包括检查点时间、CPU利用率、相邻检查点时间增量、CPU利用率变化量、内存利用率、网络传输速度，这些影响因素具有很多不确定性和随机时变特性，因此导致检查点状态发生改变时也呈现了很强的随机时变特性，并且其变化趋势只与前一个检查点状态的场景信息有关，而与其他检查点的状态无关。因此可以利用马尔可夫模型的特性来预测检查点的状态，进而对软件的异常行为及时进行调整。

2.4 软件行为可信预测框架

基于检查点场景信息的软件行为可信预测模型的框架如图2所示。在每个检查点都部署一个监测器，并为每个被监测检查点创建一个独立的信息存储队列。监测器获取到检查点的场景信息后，将监测数据暂存在对应的信息队列中，同时添加在本地监测信息库中。对每个检查点，设置一个RBF神经网络分类器，对检查点场景信息进行离线训练和在线评估，步骤如下。

图2 基于检查点场景信息的软件行为可信预测模型的框架

步骤1 离线训练。从本地监测信息库获取场景信息，训练RBF神经网络。检查点场景信息通过输入层传递到隐含层，隐含层神经元使用混合高斯激励函数对输入层的信息进行运算处理，输出层神经元对隐含层神经元的输出进行加权求和并输出结果，训练完成后，保存训练好的RBF神经网络。

步骤2 在线评估。监测器捕获软件运行时检查点的场景信息并暂存在对应信息队列，RBF神经网络分类器从检查点信息队列获取场景信息进行处理，评估当前检查点的可信情况。

然后通过半加权马尔可夫模型，得到软件在下一个检查点处于不同状态的概率或在当前检查点进行调整的概率，分为离线训练和在线评估2个步骤，介绍如下。

步骤1 离线训练。将软件运行时的第个检查点与第+1个检查点的状态信息作为样本集，训练得到第个检查点的状态概率向量，第个检查点正常或临界状态a转移到第+1个检查点状态a的概率P，用第个检查点正常或临界状态对第+1个检查点影响程度的权重对概率P加权；如果第个检查点异常，则进行人工干预，调整为正常状态的概率为P。对所有的转移概率进行规范化，得到半加权马尔可夫模型的转移概率矩阵，建立半加权马尔可夫模型。

步骤2 在线评估。在软件运行时，RBF分类器评估第个检查点的状态，若异常，则在第个检查点处进行人工干预检查；否则，根据第个检查点的状态概率向量与加权转移概率相乘得到第+1个检查点的状态概率向量，该向量中的最大概率对应第+1个检查点的可能状态。例如，检查点以较高的概率进入异常状态，通过显示器或报警器通知管理员干预检查，甚至暂停运行，进而使软件的异常运行及时得到调控。

3 基于RBF神经网络的检查点状态分类

人们一般采用语言量对信任等级进行描述，借鉴文献[14]的思想，该文将检查点状态划分为3个等级：正常状态、临界状态、异常状态。首先需要检查点场景信息样本集对RBF神经网络进行离线训练，然后利用训练好的RBF神经网络对当前检查点的状态进行评估。

采用基于伪逆的权值直接确定法[17]，可直接得到隐含层和输出层神经元之间的最优连接权值。在RBF神经网络中求解连接值时，隐含层与输出层神经元的连接权值形成矩阵，利用式(2)确定连接权值，其中，为激励矩阵，T为期望输出矩阵，则有

网络输出层第(=1,2,3)个神经元的输出为

定义网络的平均输出误差[18]为

通过训练数据集训练RBF神经网络，计算网络的平均输出误差min，然后利用校正数据集，计算网络校正的平均输出误差cur，并增加隐含层神经元的个数，若curmin，则删除新增加的隐含层神经元个数，此时网络结构已达到最优隐含层神经元数。

RBF神经网络在经过以上步骤训练后，隐含层神经元中心、方差以及隐含层和输出层之间的连接权值都被确定，这样RBF分类系统就建立起来了。

步骤2 在线评估。利用训练好的RBF神经网络分类器，就可以将监测器捕获到运行时的检查点场景信息输入RBF神经网络，评估该检查点的可信情况，若检查点状态正常或临界，则利用半加权马尔可夫模型预测下一个检查点的可信情况，否则通知管理员进行干预，甚至暂停运行。

4 基于半加权马尔可夫的检查点状态预测

4.1 检查点的场景值计算

由于场景信息中的各个因素对检查点状态的影响程度不同，因此半加权马尔可夫模型对各个属性因素采用加权的方法进行计算，求得综合场景值。采用模糊层次分析法FAHP[19]，求得各场景信息的权重，则检查点场景值计算式为

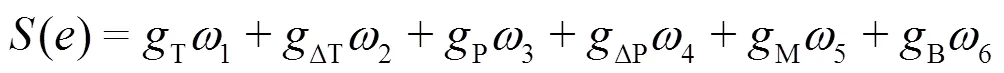
半加权马尔可夫模型依据各场景信息的相对重要程度不同，在计算场景信息的权重时数量标度如表1所示。

表1 数量标度

根据表1，按场景信息元素的重要程度，通过两两比较，建立优先关系矩阵[3]为

由于检查点的不同状态对检查点+1的影响程度不同，因此通过式(7)表示检查点+1的状态，即

在求解权重时，首先要将检查点的正常状态和临界状态对检查点+1影响程度大小进行比较，然后建立优先关系矩阵，转换成模糊一致矩阵，利用式(6)计算权值。

随着社会人口老龄化和疾病谱的改变，老年人慢性非传染性疾病的患病率高，其生活不能自理且卧床患者比例呈上升趋势。目前，社区卫生服务中心收治的对象90%以上是久卧病患，家属及保姆或陪护工等已成为他们的主要照顾和护理者(照护者)。调查发现，照护者们普遍缺乏防压疮的翻身护理知识和技能。由于照护者们对易发生压疮的这类高危人群未能正确及时掌握有效的防压疮翻身护理技能，导致发生压疮病例增多。因此，如何有效减少压疮的发生，对久卧病患照护者进行防压疮翻身护理培训值得社区护理工作者的探索。1年多来，我们加强对照护者们防压疮翻身护理技能的指导和培训，使照护者们防压疮的护理能力明显提高，现报道如下。

4.2 半加权马尔可夫模型的确定

当第个检查点处于异常时，就通知管理员对检查点进行调控，检查点从异常状态转移到干预状态，经过调整，检查点从干预状态转为正常状态。所以检查点从异常状态转移到干预状态和从干预状态转移到正常状态是必然事件，其概率34、41都为1，而从异常状态转移到其他状态是不可能事件，其概率33为0。

对第个检查点所有状态转移概率p，通过式(8)进行规范化变换，有

通过以上过程即可建立初始半加权马尔可夫模型，如图3所示。

图3 半加权马尔可夫状态转移模型

4.3 检查点的可信预测

预测过程如下。

1) 监测器捕获软件运行时第个检查点的场景信息，然后通过RBF神经网络分类器判断检查点的状态。

2) 若检查点处于异常状态，通过显示器或报警器通知管理员干预检查，甚至暂停运行。

4) 若检查点处于正常或临界状态，则通过式(9)计算检查点+1的状态概率向量+1，其中，状态概率的最大值所对应的状态即为第+1个检查点的预测状态；若显示为异常，则通过显示器或报警器通知管理员干预检查，甚至暂停运行，否则，不进行任何调整。

5 实验与分析

为了验证所提模型的有效性，在配置CPU为Intel(R)i7-6700@3.40 GHz，内存为8.00 GB、Windows版本为Windows10家庭中文版的计算机上进行了仿真实验。假设实验是在无背景噪声环境下进行的，以一个模拟累加计算器为目标程序，在程序第一轮累加开始处、第10轮累加结束处、第20轮累加结束处分别设置检查点0、1、2，即在0、1、2处置入场景信息监测器。

在检查点0与1之间随机注入干扰程序t1.start()，而t1.start()是检查点0与1之间的代码，使累加器重复运行了检查点0与1之间的代码，会引起程序的系统状态发生变化，例如，程序运行到检查点2的时间变长；在检查点0与1之间随机注入干扰程序t1.join()，而t1.join()直接调用检查点1与2之间的代码，使累加器绕过检查点1，运行了检查点1与2之间的代码，会引起程序的系统状态发生变化，例如，程序运行到检查点2时间变短；在检查点1与2之间随机注入干扰程序t1.start()，使累加器重复运行了检查点0与1之间的代码，会引起程序的系统状态发生变化，例如，程序运行到检查点2的时间变长；在检查点1与2之间随机注入干扰程序t1.join()，而t1.join()直接调用检查点1与2之间的代码，使累加器重复运行了检查点1与2之间的代码，会引起程序的系统状态发生变化，例如，程序运行到检查点2的时间变长。通过这4种随机注入干扰程序的方式模拟目标程序异常运行。在收集数据时，通过监测器捕获了目标程序以及在检查点0、1与2之间随机注入干扰程序t1.start()或t1.join()这两类程序后并行运行时检查点0、1、2的场景信息。

通过多次运行以上2类程序，直到收集了检查点1的状态转移到检查点2任一状态的所有情况，共收集了8 794条数据，每条数据包含检查点场景信息的各个指标。对于收集的数据中重复的场景信息则没有实验参考价值，所以舍弃不合理的数据后，作为实验的数据总共是8 082条。将收集的正常场景信息和异常场景信息输入RBF神经网络进行训练，对于处于两者之间的判定为临界场景信息，根据训练好的RBF神经网络对每个检查点的数据集进行分类判别。将收集的场景信息分为正常、临界、异常状态的样本，然后利用分类好的样本训练半加权马尔可夫模型的参数。RBF神经网络和半加权马尔可夫模型建立之后，就利用监测器对运行程序进行监测，根据检查点1的状态预测检查点2的状态。

5.1 RBF神经网络的建立

RBF神经网络在Matlab R2015a平台上建立，网络采用600条记录，按照70%、15%、15%的比例分为训练样本集、校正样本集、测试样本集，预设精度为0.001，学习率设置为0.01。

为了排除由于场景信息的各个指标因数量级或量纲上的差别而造成的影响，可用以下计算式进行归一化。

其中，max和min分别表示各指标中的最大值和最小值。

在训练RBF神经网络时，将检查点的场景信息作为输入，检查点状态作为输出，所以输入层神经元数量为6个，输出层神经元数量为3个，设1、2、3分别表示检查点正常状态、临界状态、异常状态，将这3个状态的输出形式分别设为[1,0,0]、[0,1,0]和[0,0,1]。若训练后应用RBF神经网络分类处理输出为[1,0,0]，则相关样本属于正常类；若RBF神经网络分类处理输出为[0,1,0]，则相关样本属于临界类；若RBF网络分类处理输出为[0,0,1]，则相关样本属于异常类。

根据神经网络的运行机制分析可知[20]，影响神经网络泛化能力的因素可以分成两类：一类是样本的影响，另一类是来自神经网络本身的影响。本实验主要分析RBF神经网络本身对其泛化能力的影响，即通过分析连接权值及训练精度对泛化能力的影响，从而确定RBF神经网络的结构。

下面，通过训练数据集、校正数据集对RBF神经网络的连接权值及训练精度进行确定，并以网络的平均输出误差为评判指标，然后测试RBF神经网络的预测能力，输入测试样本，以分类正确率为评判指标。初始设置隐含层神经元数为10个，并每次以10个训练样本进行迭代训练RBF神经网络，而且隐含层神经元个数随着样本的增加而增加，同时，通过式(2)得出网络在每次迭代训练的权值，通过式(4)得出网络的平均输出误差，直到每一个训练样本都曾被用于隐含层神经元中心，然后通过校正样本集增加隐含层神经元个数，如果此时网络的平均输出误差比训练的误差小，则校正网络的权值及平均输出误差；随着隐含层神经元个数的增加，如果此时网络的平均输出误差比前一次增加的隐含层神经元校正的误差大，则保持前一次增加的隐含层神经元个数，说明网络的平均输出误差已达到最小值，此时RBF神经网络结构建立完成。然后通过测试数据集测试网络的预测能力，检查点1与检查点2的RBF网络训练和校正的平均输出误差结果分别如图4和图5所示，测试分类的预测精度分别如表2和表3所示。

图4 检查点e1的RBF网络输出误差变化曲线

图5 检查点e2的RBF网络输出误差变化曲线

表2 检查点e1的测试分类矩阵

表3 检查点e2的测试分类矩阵

注：沿行方向是期望类别结果，沿列方向是实际类别结果。

从图4和图5可以看出，随着隐含层神经元个数的增加，RBF神经网络的平均输出误差降低，当输出误差达到最小时，继续增加隐含层神经元个数，输出误差会增大，删除使输出误差增大的多余隐含层神经元个数，确定检查点1的RBF网络的隐含层神经元数为480个，检查点2的RBF网络的隐含层神经元数为470个，所以此时检查点1与2的RBF分类系统就建立起来了。

图6 评估检查点e2状态的散点

表2和表3的状态分类矩阵实验结果表明，采用RBF神经网络能够完成对检查点1与2状态的正确分类，总的正确率分别达到95.93%和94.81%。因此可以确定此时RBF网络的预测具有很好的泛化能力。

5.2 半加权马尔可夫模型的建立

表4 0.1~0.9标度取值

采用FAHP方法计算场景信息T、ΔT、P、ΔP、M、B对应的权重，构建优先模糊矩阵为

通过以上步骤，建立初始半加权马尔可夫模型。

5.3 半加权马尔可夫模型的预测

程序在检查点1与2之间运行时间的增量最短是27.353 s，而通过检查点1状态预测检查点2状态的时间是16.239 s，这表明利用半加权马尔可夫模型进行预测是有意义的。

本实验选择50个程序周期对检查点2的状态进行评估，第1、5、8、11、15、17、23、30、37、41、44、48周期在检查点0与1之间注入干扰程序t1.start()，并行运行目标程序和注入干扰后的程序；第4、7、20、22、33、39周期使累加器正常运行；第14、23、30、34、35、36、38、40、43周期在检查点1与2之间注入干扰程序t1.join()，并行运行目标程序和注入干扰后的程序，收集这3种情况下的检查点1、2的场景信息进行实验。检查点2状态的散点评估如图6所示。

图7 评估检查点e2状态总时间开销的柱状图

1) 本文CBSI-TM模型只是在第2、29、50周期对检查点2状态的预测稍有偏差，因为在计算加权转移概率的权值时，除了检查点1是软件当前运行的场景值，检查点2所有状态的场景值都是均值，与实际稍有偏差，导致预测检查点2的状态有偏差，所以其正确率为94%，而且CBSI-TM可以对检查点2的状态进行双重评估，从5.1节测试得出，RBF分类方法对检查点2状态评估的平均正确率为94.81%，所以CBSI-TM进行双重评估的平均正确率为94.405%。

2) 当采用CBRA-TM模型评估检查点2的状态时，在第6、17、37、42周期对检查点2状态的评估与实际状态有所不同，因为通过检查点发生风险的可能性与设定的阈值对比的方式来判断检查点的状态时，阈值的设定会导致对检查点状态的评估有偏差，所以其正确率为92%。

3) 当采用RBF神经网络分类方法时，在第3、6周期对检查点2状态的评估与实际状态有所不同，因此其正确率为96%。

4) CBSI-TM模型评估的正确率低于RBF分类方法，这可能是因为在检查点1、2之间存在干扰，在检查点1预测时引起检查点1场景信息变化不明显，导致预测检查点2异常状态有偏差。

因为CBSI-TM模型可以在程序运行到检查点1时对检查点2的状态进行预测，而CBRA-TM模型和RBF神经网络分类方法只有在程序运行到检查点2时，才对检查点2的状态进行评估，所以从图7可以得到以下结论。

1) CBSI-TM模型评估检查点2状态的总时间开销比CBRA-TM模型和RBF神经网络评估检查点2状态的总时间开销明显少，RBF比CBRA-TM模型的时间开销少，这是因为CBRA-TM模型需要计算场景值并与其正常范围进行对比，才能评估检查点2的状态，而RBF通过将检查点2状态信息输入RBF神经网络即可得到检查点2的状态，因此处理检查点2信息的时间比CBRA-TM模型少，但RBF与CBRA-TM模型均是在程序运行到检查点2处，才对检查点2状态进行评估，所以总的时间开销是相似的。

2) 利用CBSI-TM模型对检查点1的状态进行评估后，预测检查点2的状态是合理和有效的，而且能实时调整半加权马尔可夫模型的参数，实现了动态预测。

3) 该实验也体现出CBSI-TM模型具有较强的针对性，只要在某个程序运行轨迹中设置检查点，发现检查点之间的状态变化规律，就能较为直观地反映软件未来运行趋势的可信情况，从而实现对软件的异常行为提前做出调控。

6 结束语

本文提出了一种基于检查点场景信息的软件行为可信预测模型，该模型通过RBF神经网络和半加权马尔可夫模型实现对检查点状态的可信评估方法，利用半加权马尔可夫模型有效地预测下一个检查点的状态，并且可以在程序运行到下一个检查点时，利用RBF神经网络分类器评估下一个检查点的状态，实现了对下一个检查点状态双重评估的效果。实验表明，该模型能够较准确和合理地预测检查点的状态来判断软件未来运行趋势的可信情况。下一步的工作将对软件的行为轨迹进行分析，进一步提高评估软件可信情况的合理性和精确度。

[1] 万烂军, 李长云, 贺宗梅. 分布式软件的交互行为监测机制的研究[J]. 计算机工程与应用, 2011, 47(5): 60-64.

WAN L J, LI C Y, HE Z M. Research on interactive behavior monitoring mechanism of distributed software[J]. Computer Engineering and Applications, 2011, 47(5): 60-64.

[2] 李珍, 田俊峰, 常卓, 等. 基于检查点的分布式软件监控与可信性评价[J]. 通信学报, 2016, 7(3): 7-18.

LI Z, TIAN J F, CHANG Z, et al. Distributed software monitoring and trustworthiness evaluation based on checkpoints[J]. Journal on Communications, 2016, 37(3): 7-18.

[3] 刘玉玲, 杜瑞忠, 冯建磊, 等. 基于软件行为的检查点风险评估信任模型[J]. 西安电子科技大学学报(自然科学版), 2012, 39(1): 179-190.

LIU Y L, DU R Z, FENG J L, et al. Trust model of software behaviors based on checkpoint risk assessment[J]. Journal of Xidian University, 2012, 39(1): 179-190.

[4] 吴佳, 曾惟如, 陈瀚霖, 等. 基于隐马尔可夫模型的软件状态评估预测方法[J]. 软件学报, 2016, 27(12): 3208-3222.

WU J, ZENG W R, CHEN H L, et al. Approach of measuring and predicting software system state based on hidden Markov model[J]. Journal of Software, 2016, 27(12): 3208-3222.

[5] GUO X, DUTTA R G, JIN Y. Eliminating the hardware-software boundary: a proof-carrying approach for trust evaluation on computer systems[J]. IEEE Transactions on Information Forensics and Security, 2017, 12(2): 405-417.

[6] 王德鑫, 王青, 贺劼. 基于证据的软件过程可信度模型及评估方法[J]. 软件学报, 2017, 28(7): 1713-1731.

WANG D X, WANG Q, HE J. Software process reliability model based on evidence and evaluation method[J]. Journal of Software, 2017, 28(7): 1713-1731.

[7] 贾晓辉, 张文宁, 刘安战. 分级的软件可信评估模型研究及应用[J]. 计算机科学, 2017, 44(4): 169-172.

JIA X H, ZHANG W N, LIU A Z. Research and application of hierarchical software trustworthiness evaluation model[J]. Computer Science, 2017, 44(4): 169-172.

[8] 王犇, 周兴社, 杨亚磊. 基于多属性熵权合成的软件可信等级评估方法[J]. 微电子学与计算机, 2014, 31(6): 21-24.

WANG B, ZHOU X S, YANG Y L. Software trustworthiness grade evaluation method based on multiattribute entropy weight synthesis[J]. Microelectronics & Computer, 2014, 31(6): 21-24.

[9] LI K W, LIU L, ZHAI J N. Reliability evaluation model of component-based software based on complex network theory[J]. Quality and Reliability Engineering International, 2017, 33(3): 543-550.

[10] OKAMURA H, DOHI T. Towards comprehensive software reliability evaluation in open source software[C]. IEEE International Symposium on Software Reliability Engineering. 2015: 121-129.

[11] LIU L, JIANG Z. Research on software reliability evaluation technology based on BP neural network[C]//IEEE/ACIS International Conference on Computer and Information Science. 2016: 1-4.

[12] 匡芳君, 王艳华, 唐贤瑛. 基于RBF神经网络的客户分类模型[J]. 长沙理工大学学报, 2005, 2(4): 70-73.

KUANG F J, WANG Y H, TANG X Y. Customer classification model based on RBF neural network[J]. Journal of Changsha University of Science and Technology, 2005, 2(4): 70-73.

[13] 许智慧. 马尔可夫状态转移矩阵的求解方法研究[D]. 哈尔滨: 东北农业大学, 2013.

XU Z H. Study on the solution of Markov state transition matrix[D]. Harbin: Northeast Agricultural University, 2013.

[14] JØSANG A. A logic for uncertain probabilities[J]. International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems, 2001, 9(3): 279-311.

[15] 刘辉, 白峰衫. 基于混合高斯过程模型的高光谱图像分类算法[J]. 高校应用数学学报, 2010, 25(4): 379-385.

LIU H, BAI F S. Hyperspectral image classification based on mixed gaussian process model[J]. Applied Mathematics & A Journal of Chinese Universities, 2010, 25(4): 379-385.

[16] 王爱萍, 张功营, 刘方. EM算法研究与应用[J]. 计算机技术与发展, 2009, 19(9): 108-110.

WANG A P, ZHANG G Y, LIU F. Research and application of EM algorithm[J]. Computer Technology and Development, 2009, 19(9): 108-110.

[17] 张雨浓, 李克讷, 谭宁. 中心、方差及权值直接确定的RBF神经网络分类器[J]. 计算机技术与自动化, 2009, 28(3): 5-9.

ZHANG Y N, LI K N, TAN N. RBF neural network classifier with center, variance and weight directly determined[J]. Computer Technology and Automation, 2009, 28(3): 5-9.

[18] 张雨浓, 王茹, 廖柏林, 等. 权值与结构双确定法的RBF神经网络分类器[J]. 计算机技术与自动化, 2014, 33(3): 1-7.

ZHANG Y N, WANG R, LIAO B L, et al. Both weights and structure determination method of RBF neural network classifier[J]. Computer Technology and Automation, 2014, 33(3): 1-7.

[19] 张吉军. 模糊层次分析法[FAHP][J]. 模糊系统与数学, 2000, 14(2): 80-88.

ZHANG J J. Fuzzy analytical hierarchy process[J]. Fuzzy Systems and Mathematics, 2000, 14(2): 80-88.

[20] 周文冬. 基于PSO的自组织RBF神经网络优化设计及应用研究[D]. 北京: 北京工业大学, 2016.

ZHOU W D. Optimazation and applizaction of self-organizing network based on PSO[D]. Beijing: Beijing University of Technology, 2016.

[21] 骆正清, 杨善林. 层次分析法中几种标度的比较[J]. 系统工程理论与实践, 2004(9): 51-60.

LUO Z Q, YANG S L. Comparative study on several scales in AHP[J]. Systems Engineering Theory and Practice, 2004(9): 51-60.

Software behavior trust forecast model based on check point scene information

TIAN Junfeng1,2, GUO Yuhui1,2

1. School of Cyber Security and Computer, Hebei University, Baoding 071002, China 2. Key Lab on High Trusted Information System in Hebei Province, Baoding 071002, China

In order to ensure the trustworthiness of software, and evaluate the trusted status of the software after running for a period of time by monitoring software behavior dynamically, a software behavior trust forecast model on checkpoint scene information which was called CBSI-TM was presented. The model set up a number of checkpoints in the software running track, and introduced the time increment of adjacent checkpoints, and the change of CPU utilization rate to define the scene information, and reflected the relationship between adjacent checkpoints scene information. Then the RBF neural network classifier evaluated the status of the current checkpoint to judge the trustworthiness of the software, and the semi weighted Markov model predicted the situation of the next checkpoint to evaluate the trustworthiness of future running trend of the software. The experimental results show that the CBSI-TM model can predict the future trusted status of the software effectively, and verify that the model is more reasonable and effective.

software trustworthiness, check point, RBF neural network, semi weighted Markov model

TP393.08

A

10.11959/j.issn.1000−436x.2018163

田俊峰（1965−），男，河北保定人，河北大学教授、博士生导师，主要研究方向为信息安全与分布式计算。

郭玉慧（1992−），女，山西朔州人，河北大学硕士生，主要研究方向为信息安全与分布式计算。

2018−01−09；

2018−07−30

国家自然科学基金资助项目（No.61170254）；河北省自然科学基金资助项目（No.F2016201244）

The National Natural Science Foundation of China (No.61170254), The Natural Science Foundation of Hebei Province (No.F2016201244)