LVDT传感器相位移研究
郑嘉铭,王 银
(1.沈阳工业大学电气工程与自动化学院,辽宁 沈阳 110870 2.南京机电液压工程研究中心,江苏 南京 211106)
军工装备产品的技术要求普遍较高,在伺服控制系统中,各控制部件的控制精度的高低将直接影响系统的动态品质。传感器是伺服控制系统的重要组织部件之一,用于检测系统的实时状态,提供精确的反馈信号,并参与系统的控制[1]。本文研究的LVDT(线性可变差动变压器)是一种测量直线位移的电感式传感器,作为作动器或滑阀的位置反馈单元,广泛应用于军用战斗机航空液压作动系统中。目前在航空液压伺服控制系统的动态性能设计过程中关注点往往多放在液压伺服阀上,对伺服阀的动态频响提出很高的要求,而对传感器特性对系统动态影响的研究较少,更多的研究集中在对电感式传感器的线性度的分析上,一般借助系统仿真建模方法,开展磁场分布特性的分析,从而得到传感器结构参数对线性度的影响[2-3],包括对传感器技术制造工艺,如绕制方法、精密合金材料选材等方面[4]。电感式传感器的输出相位移对系统的动态性能同样会产生较大的影响,相位移过大将会削弱系统的动态品质,降低随动系统的跟随性能。事实上,国外传感器厂商如TE提供的产品相位移均在6°以下[5-6],而我国航空传感器的相位则在十几度,与国外存在较大差距。因此展开传感器相位移机理研究对于提高传感器的设计水平具有重要意义。
本文通过对LVDT传感器输出相位移的系统研究,得到了影响传感器相位移的关键因素,为传感器的性能设计提供参考依据。
1 理论分析
LVDT传感器由线圈组件、线圈骨架、铁芯组件和外壳体组成。线圈组件是在线圈骨架上密绕好初级线圈,然后在初级线圈上绕制两个次级线圈,为了保证传感器具有较高的线性范围,通常次级线圈匝数密度按线性函数分布。
在理论计算过程中,传感器初级线圈可等效为螺线管,其线圈架结构见图1所示。并进行如下假设:一是在线圈架垂直于轴线的截面内磁感应强度是相同的,二是忽略空气段的传感器电压输出[7-8]。

图1 线圈架分析模型
空线圈内的磁感应强度[9-10]为
(1)
式中:Bl为空线圈内磁感应强度;I为初级线圈电流;N为初级线圈匝数;μ0为空气磁导率;l为线圈架有效长度;x为空线圈内任一位置;r为线圈架直径。
该函数为关于骨架长度l和骨架中空半径r的减函数,因此可以将该函数简化写成:

(2)
衔铁的磁感应强度为
w∈[-0.5la,0.5la]
(3)
式中,UEXC为激励电压;Z为初级线圈阻抗;μr为衔铁磁导率;w为衔铁任一位置;la为衔铁长度;ra为衔铁直径;Ba为衔铁内磁感应强度。
该函数为关于铁芯长度la和铁芯半径ra的减函数,因此可以将该函数简化写成:
(4)
将式(2)代入式(4)得到铁芯的磁感应强度:

(5)
可以简化为
(6)
以骨架有效长度176 mm;铁芯长度为100 mm;初级线圈4220匝的线圈架进行计算,得到0 mm位移时空线圈架在铁芯处的磁感应强度和加入铁芯后,铁芯的磁感应强度,如图2所示。骨架内部磁场强度保持恒定,铁芯磁场强度处两端外也保持恒定。

图2 空线圈磁场分布与铁芯磁场分布
两次级的感应电压为:
(7)

(8)
初级与两次级的电流分别为:
(9)
(10)

(11)
式中,Sa为衔铁截面积;R,Ra,Rb为传感器初级和次级电阻;L,La,Lb为传感器初级和次级电感。
从公式中可以看出影响传感器感应电流相位的主要参数是传感器初级的阻抗与次级的阻抗。
2 仿真分析
本文以某型电液伺服阀阀芯位置传感器的设计为背景进行仿真分析。解调系统采用的是AD598芯片,其采用的解调方式为传感器两次级的差值除以两次级的和值作为灵敏度,为了保证传感器的差值线性及和值恒定采用了全阶梯的方式进行绕制[11-12]。传感器的绕组形式见图3。

图3 AD598芯片及绕组形式
本文进行了2次仿真,传感器的次级绕组均相同,仅改变传感器的初级绕组。第一次试绕采用铜芯直径为φ0.07 mm的漆包线,初级绕组密绕5层。第二次试验采用铜芯为φ0.1 mm的漆包线,密绕11层。在位移2 mm时第6个周期得到传感器的输出如图4。将波形相位时间差换算为角度,则得到次级1对初级的相位角分别为40.1°和16.9°。差值输出分别为0.60 V,0.50 V。和值输出分别为1.32 V,1.21 V。其相位减小了23.2°。差值为原来的83.3%;和值为原来的91.7%。
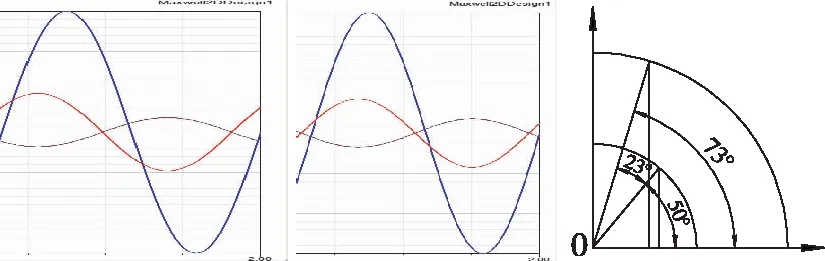
图4 不同初级绕组下的相位及阻抗相位角
两组线圈初级的电阻与阻抗与线圈有效安匝数见表1。第一次仿真初级的电阻、阻抗相差为50°,第二次仿真初级的电阻、阻抗相差为73°。两组线圈阻抗的相位差为23°,其值等于两次仿真时次级1与初级的相位差23.2°。因此认为初级电阻、阻抗相差决定了传感器的输出相位角。

表1 仿真参数对比
3 试验验证
对仿真模型进行试验验证,被试传感器为某型电液伺服控制系统的位置反馈传感器,为了验证上节中所述仿真结果的正确性,在不改变传感器自身骨架和铁芯结构尺寸的前提下,对传感器初级、次级线圈的有关参数分别进行了两次调整,并通过试验,分别测量不同位移处初级和次级线圈的电阻和阻抗以及传感器的输出相位移,测试结果见表2和表3。其中,绕制传感器时第一次传感器采用了 φ0.07的漆包线绕制,第二次传感器采用了φ0.1的漆包线绕制。由于第二次传感器达到相近的电阻值,需要更多的匝数,因此传感器的阻抗变化较大。

表2 第一次传感器的实测数据
注:传感器的激励电压为3 Vrms/3000 Hz,电气行程-2 mm~+2 mm。

表3 第二次传感器的实测数据
注:传感器的激励电压为3 Vrms/3000 Hz,电气行程-2 mm~+2 mm。
以0 mm处作为研究对象,两次初级绕组阻抗相位差为19.1°,与实测的传感器次级1对传感器初级的相位差19.8°一致。以2 mm处作为研究对象,初级相位差为17.9°,与实测的传感器次级1对传感器初级的相位差18.8°相一致,如表4。

表4 计算相角
实验结果与理论分析和仿真分析很好地对应。因此认为传感器的相位差主要由传感器的初级电阻与阻抗的相位角决定。
4 结束语
经本文的理论分析、电磁仿真与试验验证表明,传感器的相位移主要受传感器的初级线圈电阻与阻抗的相位角影响。为了减小传感器的相位移,同时保持传感器的输出电压差值不变,可以增大初级线圈的线径,目的是减小电阻;同时保证传感器初级绕组的有效安匝数不变,目的是保持阻抗不变。相位移的大小决定于传感器初级线圈电阻与阻抗的比值,对于频率响应要求较高的伺服作动系统,由于相位移过大会降低其动态品质,因此应尽可能地减小该比值,以获得较好地相位移。

