基于神经模糊PID的ABS控制策略研究
马忠武,倪兰青,陈宇珂,张会琪,林 棻
(1.江苏金坛长荡湖新能源科技有限公司, 江苏 常州 213200;2.南京航空航天大学 能源与动力学院, 南京 210016)
作为一种主动安全装置,ABS能有效防止车轮抱死、侧滑、甩尾,提高汽车的制动性能,同时具有较好的横向稳定性。在汽车制动过程中,维持轮胎和地面之间的最大摩擦力和保持车轮滑移率在最佳范围之内是ABS的控制目标[1],当前对汽车ABS控制算法的研究和改良仍是汽车研究中的重要课题。
文献[2]研究了PID控制原理,将车轮滑移率作为研究对象,并与无PID控制时相比较,验证了PID控制器对ABS系统的调节作用,但该控制策略鲁棒性有待提高。文献[3]分析了基于车速估计和地面附着系数估计的汽车ABS滑模控制,在车速和路面条件未知的情况下就可以控制汽车ABS,但该控制策略实时性较差,难以运用到实时系统之中且滑模控制在滑模面容易出现震荡。Dincmen等[4]、Necaibia等[5]将最优控制应用于汽车ABS控制之中,建立目标函数并自动寻求最佳极值点,使轮胎地面附着系数最大化。但ABS作为一个非线性系统,控制效果的优劣主要依赖于系统的数学模型,控制质量难以把握。以上控制策略参数往往是不可变化的,均可以在线性系统和简单单一路面上取得较好的制动效果,但在非线性系统和复杂路面上的控制效果不是十分理想。文献[6-8]在PID控制的基础上,将模糊控制应用于ABS,根据路面情况的变化在线调整PID参数,结果显示:模糊PID控制在制动性和适应性上的表现比PID控制更好,具有较强的鲁棒性。模糊控制(FLC)作为一种智能控制系统,能实现在线调整PID参数。模糊控制的自身性能取决于模糊规则及其合成推理,但通常模糊控制器的语言规则和合成规则往往是不可调整的,但汽车在实际行驶过程中路面条件总是不确定和不断变化的,固定不变的模糊规则很难适应时变的实际系统,不能根据路面情况的变化而做出调整,很难达到满意的控制效果。
本文提出一种神经模糊控制系统,通过神经网络的学习,使模糊规则的生成和调节转变为神经网络加权系数的调节。人工神经网络是建立在对人大脑研究的基础上发展起来的,它的主要目的是仿照人体大脑的基本运行机理,最终实现智能化的控制[9-11],其主要优势是具有强大的自学能力和推理能力,而模糊控制需要建立复杂的模糊规则。将神经网络和模糊控制相结合,利用神经网络的学习方法,根据输入输出的学习样本自动设计和调整模糊系统的设计参数,实现模糊系统的自学习和自适应功能,可以解决模糊系统中的知识抽取问题,大大降低建立系统的难度,系统将智能化的代理人们处理各种繁杂的工作。因此,本文将自适应神经模糊PID控制应用于汽车ABS控制之中,神经模糊推理系统以理想滑移率与实际滑移率之差e作为输入,以传统PID控制器的3个参数Kp、Ki、Kd为输出,利用模糊规律和神经网络算法实现对参数Kp、Ki、Kd的在线调整,以满足不同时刻误差e对PID参数自整定的要求,因此该系统具有较强的鲁棒性和良好的自适应能力。
1 汽车ABS建模
1.1 汽车二轮车辆模型
本文采用二轮车辆模型作为车轮动力学模型[12],如图1所示。

图1 二轮车辆模型
汽车在纵向方向的运动方程为:
max=-Fx1-Fx2
(1)
车轮运动方程为:
(2)
J2ω2=Fx2R-Tb2
(3)
车轮纵向摩擦力为:
Fx1=μ1N1
(4)
Fx2=μ2N2
(5)
前后轮法向载荷为:
(6)
(7)
式(1)~(7)中:R表示车轮滚动半径;ω1、ω2分别为前后轮角速度;Tb1、Tb2分别表示前后轮制动器制动力矩;Fx1、Fx2分别为前后轮地面制动力;N1、N2分别为前后轮法向载荷;μ1、μ2分别表示前后轮与地面间的制动力系数;m表示汽车质量;L表示前后轴间距离;L1、L2分别表示质心与前后轴间距离;hg表示汽车质心高度;J1、J2分别表示前后轮的转动惯量。
1.2 轮胎模型
轮胎作为汽车的重要组成部分,研究制动过程中它所受附着力与其他各种参数的关系有重要意义。本文主要研究车辆直线制动行驶,不考虑轮胎所受的横向作用力,故本文选用魔术公式[13]表达轮胎特性:
μ=Asin{Btan-1[Cλ-tan-1(Dλ)]}
(8)
魔术公式中:A、B、C、D是与路面有关的常数,反映了不同的路面;λ为车轮滑移率;μ为轮胎地面间制动力系数。图2为不同附着路面条件下μ-λ关系曲线。

图2 三种不同路面μ-λ曲线
从图2中可以看出:滑移率λ在15%到20%之间时制动力系数最大;之后,滑移率增加,制动力系数明显下降,且不同路面条件下地面可利用附着系数和最佳滑移率也是不一样的。因此,本文ABS控制目标即将车轮滑移率始终控制在最佳滑移率附近,可以将轮胎地面可利用附着系数维持在最大范围并有效防止车轮抱死。
汽车在制动过程中滑移率计算公式如下:
(9)
其中:λ为滑移率;v为车速;R为车轮半径;ω为车轮转动时的角速度。在纯滚动时,v=Rω,滑移率λ=0;纯拖滑时,ω=0,λ=100%;边滚边滑时,λ在0~100%。滑移率的值说明了车轮运行中滚动成分所占的比例。
1.3 制动系统模型
制动系统包括传动机构和制动器两部分。因此对制动系统的建模包括传动机构建模和制动器建模两部分[14]。
制动器力学模型描述了制动轮缸压力输入以及制动力矩输出之间的力学特性,尽管液压阀的形式可以不同,但在制动增压的过程中,进入制动缸的流量为
(10)
式中;Q为进入制动缸的液体流量;Cd为流量系数;Ad为控制阀过流面积;Ps为油源压力;P为制动缸压力;ρ为油液密度。
制动缸压力变化率满足:
(11)
式中:V0为制动缸及管路的总容积;βe为油液的体积弹性模量。
由流量公式和滑移率公式可知:
(12)
(13)
对于开关阀ki,由式(13)可知制动缸压力变化率不是常数,而是随制动缸的压力升高而降低。
同理,在减压过程中,制动缸油压的变化率为:
(14)
式中:kd为与阀结构有关的参数;Pr为回油管路的压力。
如果忽略非线性和温度的影响,制动力矩Tb可以看作是制动压力P的线性函数,即:
Tb=(P-Pout)AwcηBFrr
(15)
式中:Pout为所谓的推出压力;Awc、η、BF、rr为常数。
控制的目的是按照一定的控制规则,控制加在每个车轮的制动力矩及控制液压回路的电磁阀通断回路,实现增压、保压和减压,防止车轮抱死,使车轮滑移率保持在理想范围之内,以保证制动的稳定性。
2 汽车ABS路面自动识别系统
由图2可知:在不同路面上,车轮的最佳滑移率和地面最大制动力系数是不一样的。因此,为了适应不同的路面并充分利用地面可提供的附着系数,加入路面识别系统,使汽车在路面情况发生变化时轮胎始终保持在最佳滑移率并维持地面最大制动力[15]。
根据车轮运动方程式(2)可得
(16)
式中:ω为车轮理论角速度;μ为路面附着系数;N为地面对车轮的法向反作用力;R为车轮半径;Tb为制动器制动力矩;J为车轮转动惯量。
由于不同路面上车轮滑移率与制动力系数的关系曲线(μ-λ曲线)不同,因此同一滑移率所对应的地面制动力系数也是不同的,故由式(16)可知:不同路面上车轮的理论角减速度也是不同的。通过将系统输出的车轮实际角减速度与车轮理论角减速度进行比较,当其差值最小时所对应的路面即为汽车当前行驶的路面。路面识别系统即可及时识别出当前路面情况对应的最佳滑移率,这在复杂多变的路面上尤为重要。路面识别系统的控制流程如图3所示。

图3 路面识别系统的控制流程
路面自动识别系统能够实时确定当前汽车行驶的路面。从而根据辨别出的路面设定系统的期望滑移率,保证汽车在变附着系数路面上能够时刻保持最佳滑移率和最大附着系数。然后利用ABS控制器在线调整制动器制动力矩,使车轮滑移率维持在目标滑移率附近。控制框图如图7所示。
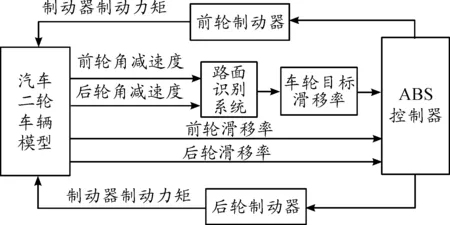
图4 路面识别系统控制框图
3 神经模糊PID控制
神经网络模糊PID控制器的结构如图3所示。

图5 神经模糊PID控制器结构框图
神经模糊PID控制器由3部分组成:PID控制器、模糊化模块、神经网络控制器[16]。其输入为理想滑移率与实际滑移率之差,即:
e=r(k)-y(k)
(17)
其中:r(k)为车轮理想滑移率;y(k)为车轮实际滑移率。该控制器输出为PID控制器参数Kp、Ki、Kd的变化量,进而调节车轮制动器制动力矩,保证汽车的制动稳定性。
3.1 PID控制器
PID控制器用于调节ABS液压系统,进而使车轮滑移率保持在理想范围之内。PID控制由比例单元P、积分单元I和微分单元D组成[17-19]。其算法表达式为:
(18)
但传统的PID控制器参数是不变的,难以适应复杂多变的路面。于是本文采用一种参数自调节系统自动调节PID参数,即神经模糊系统。
3.2 模糊化模块
模糊化模块对系统的误差变量e进行模糊化和归一化处理,即根据输入变量模糊子集的隶属度函数找到对应的隶属度的过程。
在设计的基于神经网络模糊PID控制器中,模糊集合的论域为[-6,-5,-4,-3,-2,-1,0,1,2,3,4,5,6],输入的语言为{NB,NM,NS,O,PS,PM,PB}。三角函数灵敏度较强,因此隶属度函数采用三角函数。为增强系统的鲁棒性,提高隶属度函数的分辨率,在0值附近的三角函数形状设计的更陡一些[17],隶属度函数如图6所示。
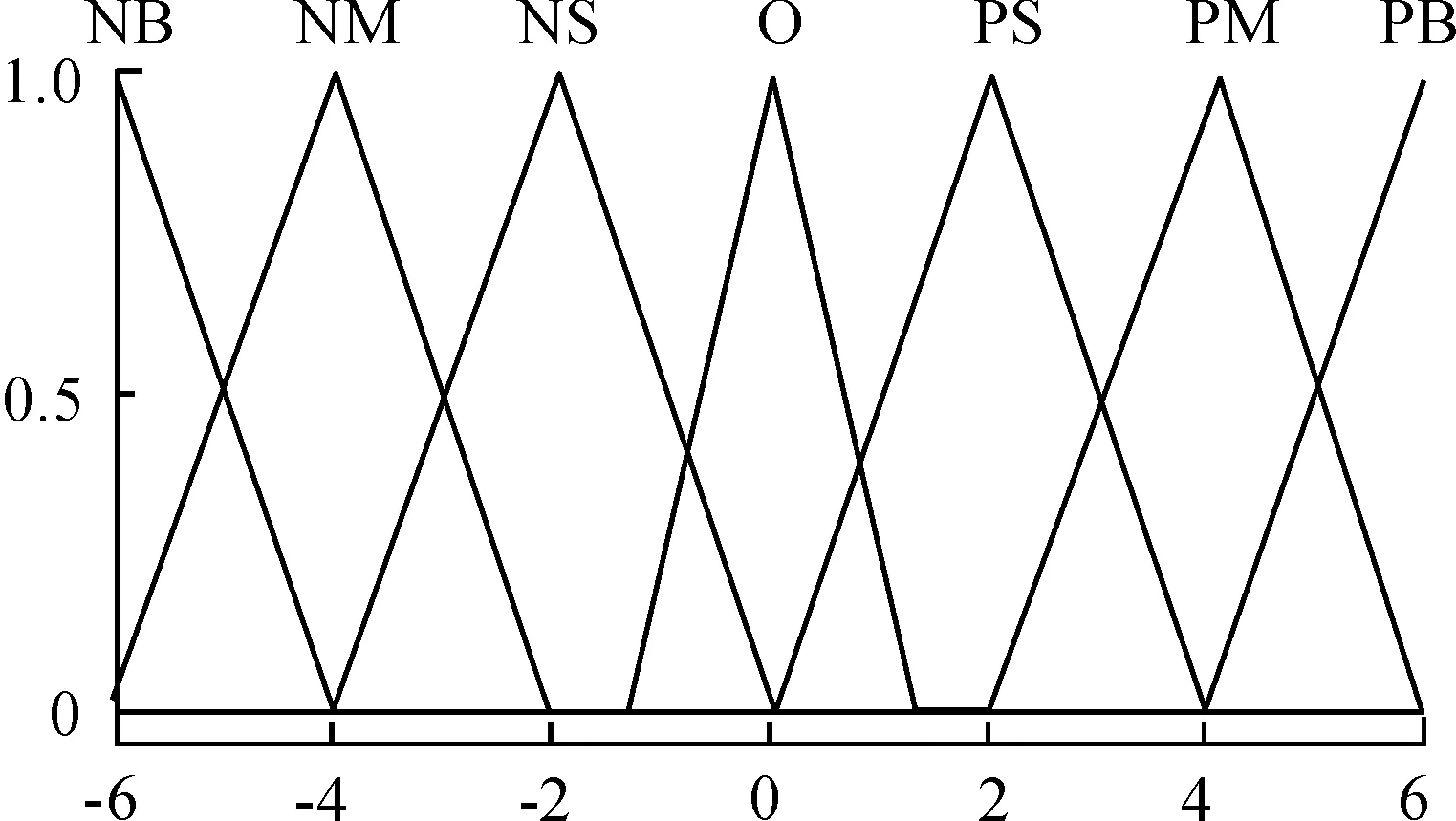
图6 误差e的隶属度函数
3.3 神经网络控制器
神经网络用于生成模糊规则。通过神经网络的自学习能力,使模糊规则的生成转变为加权系数初值的确定和调节。进而调整PID控制器参数以控制汽车ABS,利用PID控制器的输出u来调整汽车ABS制动器的制动力矩。
本文采用3层BP神经网络。BP神经网络是一种有导师学习的前馈型神经网络,它的学习规则是最速下降法,通过反向传播来不断调整网络的权值和阈值,使网络的误差平方和最小[20-23]。其结构包括输入层、隐含层和输出层,如图5所示。
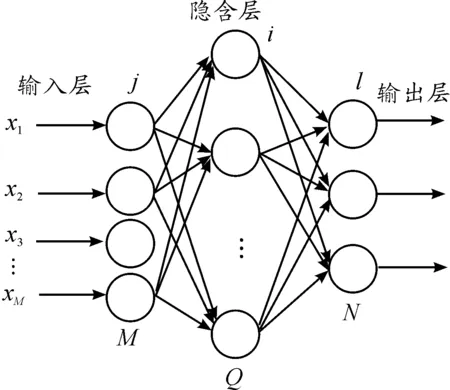
图7 BP神经网络结构
该BP神经网络有4个输入节点、8个隐含节点、3个输出节点,即M=4,Q=8,N=3。输入节点对应经模糊量化后的系统状态变量。
BP神经网络的前向计算过程如下:
输入层输出为:
(19)
其中M=4,M的选取取决于被控系统的复杂程度。
隐含层输入输出为:
(20)

(21)
神经网络输出分别对应PID控制器的3个可调参数。网络输出层的输入输出分别为:
(22)
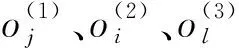
(23)
取性能指标函数进行BP神经网络误差反向传播[18],性能指标函数为
(24)
对样本p完成加权系数的调整后,再输入另一个样本进行学习,直到完成所有样本的训练。本文采用遗传算法优化神经网络初始权重。神经网络的训练分为两步:第1步采用遗传算法优化初始权重,第2步利用BP算法完成网络训练。
用最速下降法调整网络的加权系数,即按照误差函数E(k)对加权系数的负梯度方向调整,并附加一个使搜索快速收敛全局极小的惯性项,则有:
(25)
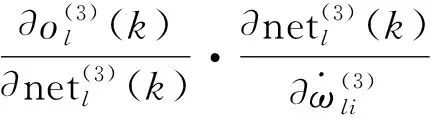
(26)
式中η为学习速率,η>0。学习速率η对加权系数的调整非常重要。本文采用变学习速率方法,令学习速率η随着学习的进展逐渐减小,可得到较好的效果,引入惯性系数α的办法,也可使收敛速度加快,α的取值可选在0.9左右。
可推导得出BP神经网络输出层的加权系数调整公式为:
(27)
同理可得隐含层加权系数的调整公式为:
(28)
式中,
(29)
4 仿真结果与分析
对本文提出的神经模糊PID控制方法进行仿真分析,并对传统PID控制方法进行制动距离仿真对比。仿真工况如下:初始车速90 km/h,路面分别为高附着系数路面、低附着系数路面和高低附着系数对接路面。仿真路面宽度为3.7 m,仿真步长设定为0.01 s。在高低对接路面工况汽车从高附着系数路面上起步,经0.2 s开始制动,并设置高附着系数路面长度为30 m,汽车行驶30 m后进入低附着系数路面直到汽车制动停止。通过路面识别系统自动识别高低附着系数路面并设置路面理想滑移率。本文选用的整车参数如表1所示。

表1 汽车整车参数
4.1 高附着系数路面
图8、9分别为神经模糊PID控制下的前后轮滑移率及速度对比图,图10为神经模糊PID控制与传统PID控制的制动距离对比。由以上仿真图像可得:在高附着系数路面上,神经模糊PID控制下车速下降十分平稳,滑移率波动较小,能在较短时间迅速地使车辆达到最佳滑移率,制动比较稳定,制动距离为36.2 m,而传统PID控制策略的制动距离为38.4 m,制动性能较好。
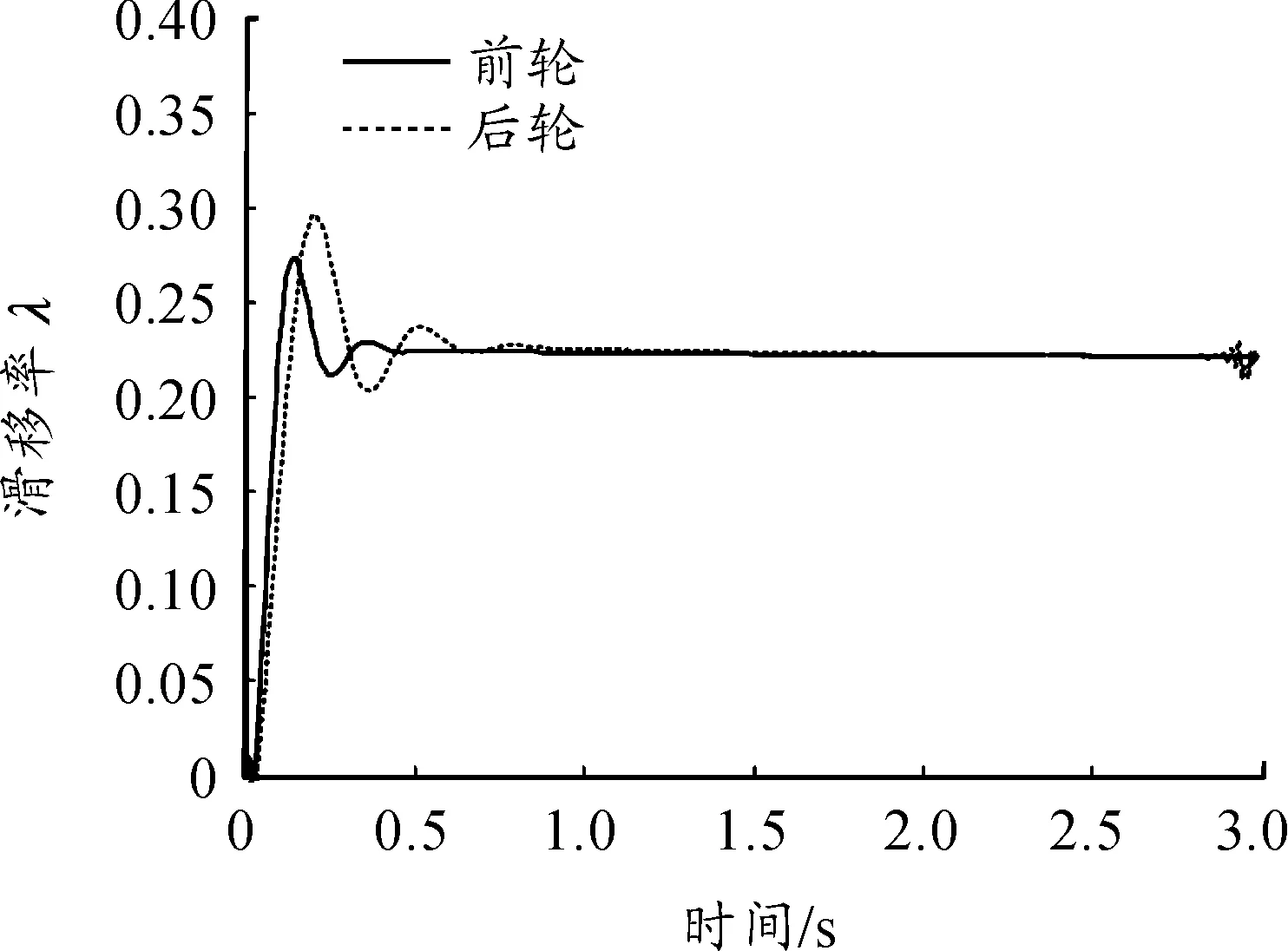
图8 滑移率曲线(高附着系数路面)

图9 车速轮速对比 (高附着系数路面)
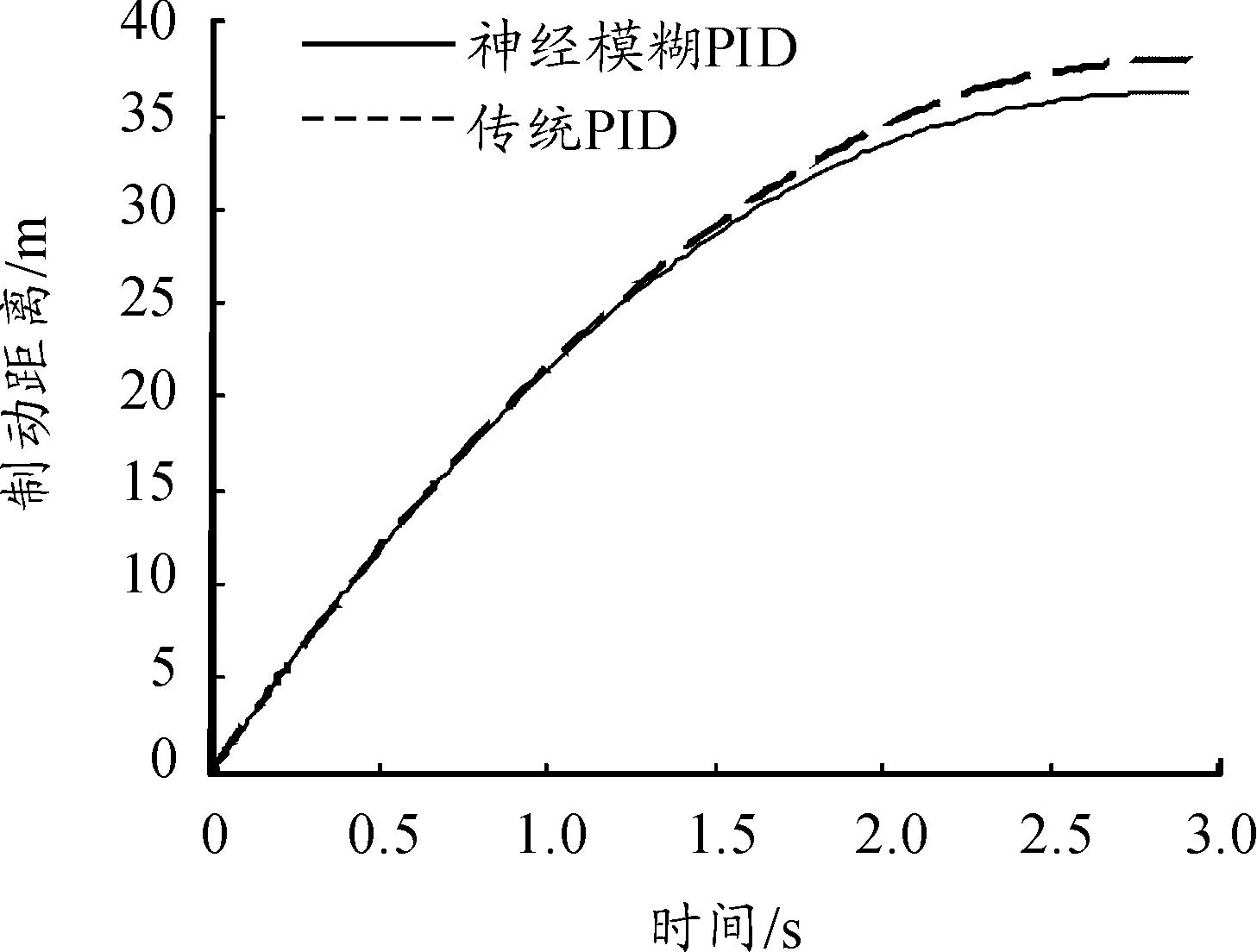
图10 制动距离曲线对比(高附着系数路面)
4.2 低附着系数路面
由图11~13可得:车辆在低附着系数路面上车速曲线和滑移率曲线在制动开始时有些波动但能很快消除;在汽车即将停止时滑移率曲线出现震荡。这是因为汽车制动要结束时制动力矩波动较大,而路面附着系数较低,制动力矩的微小变化就会引起滑移率的变化,但当时车速较低,因此不会对制动稳定性产生影响。同时制动距离为95 m,比传统PID控制策略短。
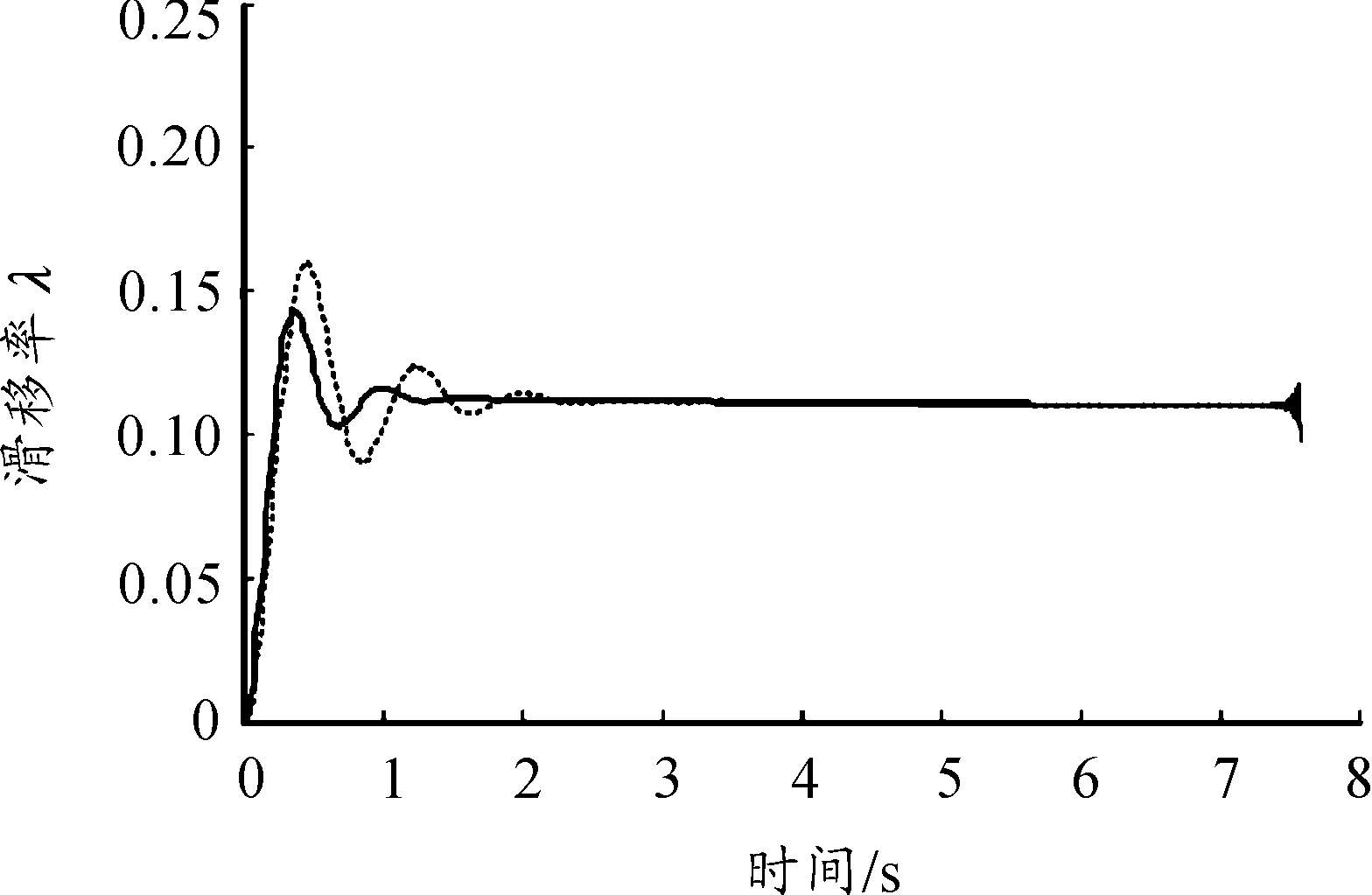
图11 滑移率曲线(低附着系数路面)
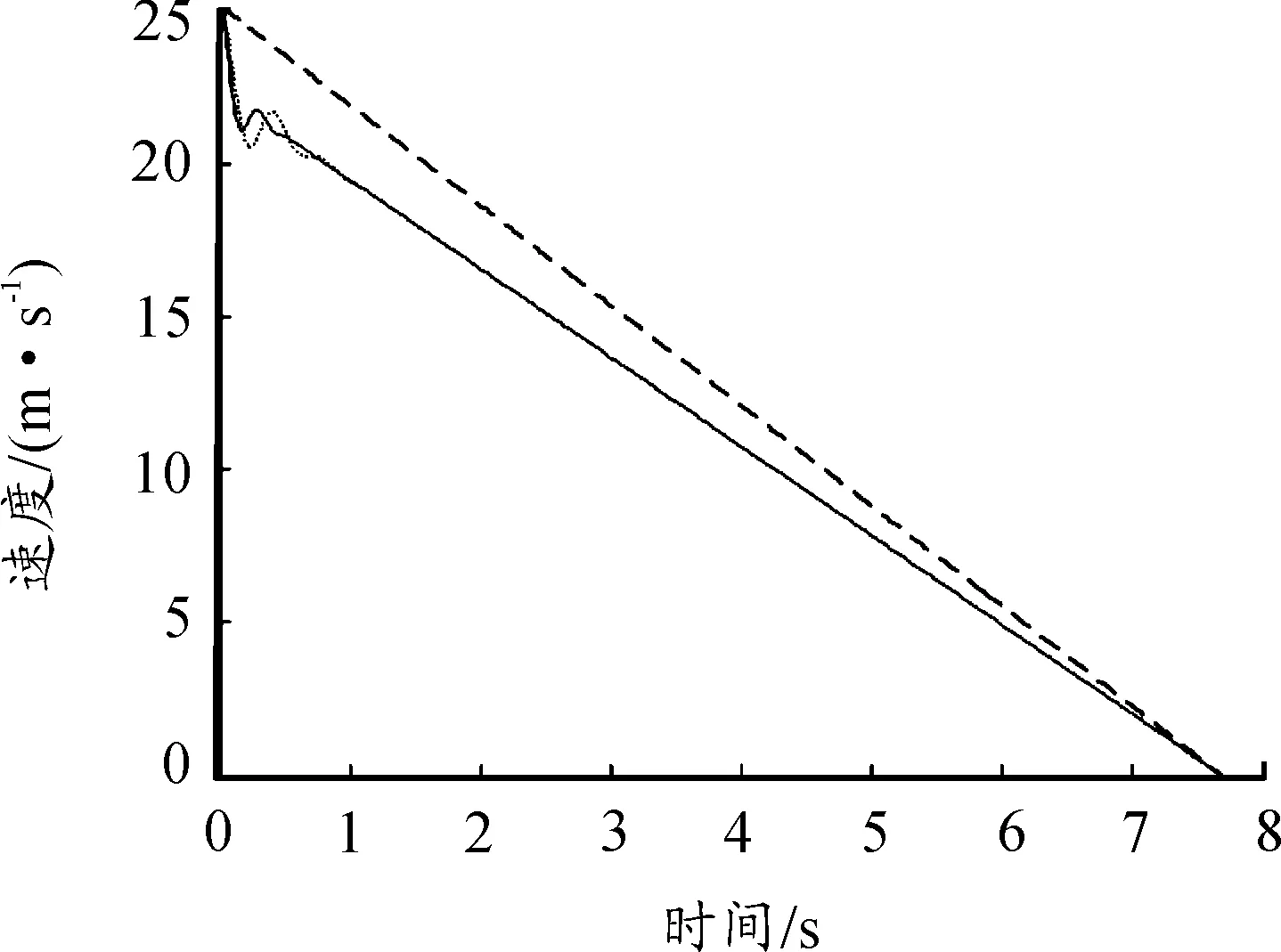
图12 车速轮速对比(低附着系数路面)
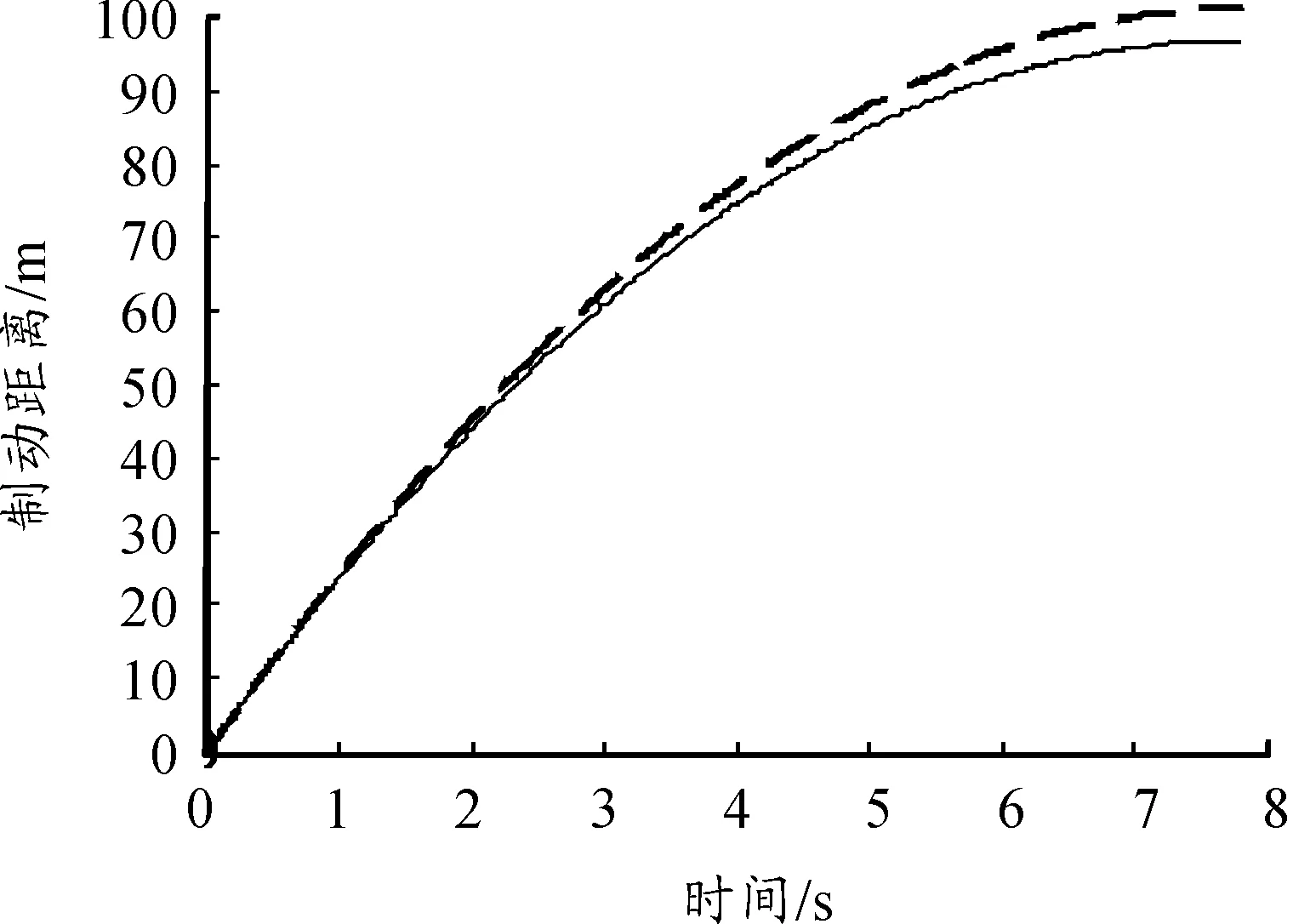
图13 制动距离曲线对比(低附着系数路面)
4.3 对接路面
由图14~16可知:汽车在对接路面上制动时神经模糊PID的制动距离为57 m,较传统PID的制动距离更短;车辆在制动开始1.8 s时由高附着系数路面驶入低附着系数路面路面,在路面条件发生变化时,滑移率和车速曲线出现较小突变,并且快速恢复稳定。这表明采用的路面识别系统能够有效识别出路面的变化,并且神经模糊PID控制算法中的神经网络能够根据实际路面情况及时调整模糊规则,以适应突变的路面而传统PID控制策略下则无法识别路况变化,制动所需时间更长,充分体现了神经模糊PID控制的优越性。

图14 滑移率曲线(对接路面)
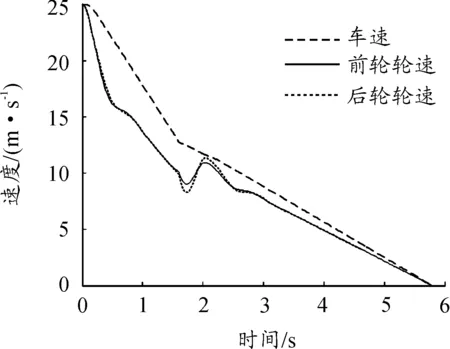
图15 车速轮速对比(对接路面)
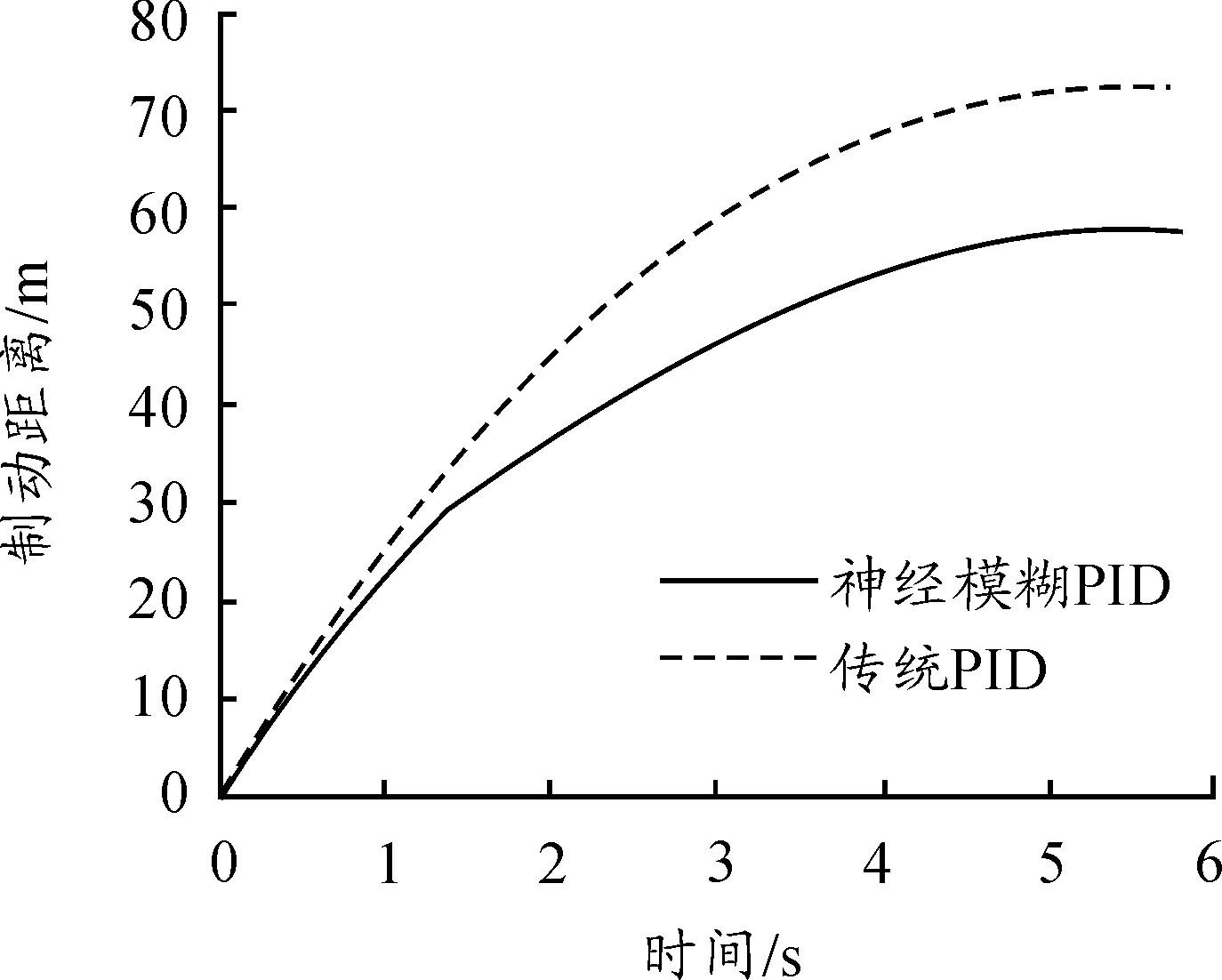
图16 制动距离曲线对比(对接路面)
5 结束语
介于车辆在实际制动时路面条件总是变化的,本文建立了路面识别系统,并采用神经模糊PID控制实现了控制器参数的实时调整,以适应复杂多变的路面。仿真结果表明:本文所提出的神经模糊PID控制算法在高附着系数路面、低附着系数路面和对接路面上均能取得理想的制动效果,有较高的制动稳定性。

