运用Objective-C实现Fry法有限应变测量
曾荣杨,张夏永,李建
(1.成都理工大学地球科学学院,四川成都 610059;2.重庆杭畅科技有限公司,重庆 400039)
有限应变测量是对韧性变形岩石进行变形量和构造运动学定量估算的主要方法,是韧性剪切带构造属性与构造分带的关键判据之一,但一般要求大量的应变标志体测量结果并进行数据统计分析[1]。应变测量是研究地质构造重要的一环,其中又以Fry法有限应变测量应用最为普遍。Fry法是一种简单直观的应变测量方法,以变形颗粒(砾石、鲕粒、等轴矿物)为应变标志体,广泛应用与地质实践[2]。本法适用于均匀(随机)分布颗粒的岩石,虽然天然岩石中各个颗粒(标志体)的分布是随机、无规律的,但由于各个颗粒(标志体)的分布是均匀的,因而可以将不同点的坐标叠加在一起,从而能够形成形状似“椭圆”的点的集合。
虽然有前人在计算机上实现过Fry有限应变测量的实现,但是其在操作性、方便性方面仍然不足,因此本文通过Fry法在Objective-C平台上的应用,实现了移动设备上的Fry图解,更为方便、快捷。
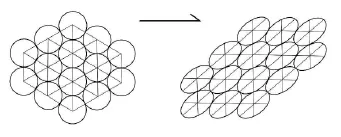
图1 岩石各个颗粒(标志体)变形前后Fig.1 Before and after the deformation of rock particle(markers)
设想物体和岩石在变形前内部某一点为一小圆球体,变形后这个圆球体就会变成一个椭球体[3];变形前各个颗粒(标志体)的距离在各个方向上都是相等的,在变形后各个颗粒(标志体)的距离变成各向异性。
1 传统Fry应变测量方法及步骤
1.1 岩石各个颗粒(标志体)中心点的标定
岩石在变形以后,岩石各个颗粒(标志体)中心的相对位置会发生改变。对于露头或标本切面上的标志体,一般将透明纸蒙在其上,点出标志体的中心;对切片尺度内的标志体,目前一般采取放于放大的显微照片上,用透明纸点取[4]。一般得到切片显微图后,将切片显微图片投影到屏幕上,再将透明纸蒙到屏幕上,标定岩石各个颗粒(标志体)中心的位置,并按照1、2、3……N的顺序将标定的点编号。岩石颗粒中心标定如图2所示。

图2 岩石各个颗粒(标志体)中心的标定Fig.2 Marking of the rock particle(markers)
1.2 将中心点映射到透明纸上
另取一张透明纸,在其中心位置标出“十”及坐标系。再将第二张透明纸的“十”移动到第一张纸的点1,并将其他点投影到此透明纸上;重复上述步骤,直到将坐标原点与第一张纸的所有点(1、2、3……N)重合为止。这一步两张透明纸的相对方向不能发生改变。
1.3 图解
通过重复以上步骤,透明纸上的点不再是均匀分布了。不难发现,在中点“十”附近出现点密度极低的空白区,呈椭圆形[5],即Fry图解。测量出其长轴dmax、短轴dmin以及应变椭球主轴方位α,即可计算出轴比R。
2 运用Objective-C实现Fry法应变测量(算法及代码)
2.1 Objective-C简单介绍
Objective-C是一种通用、高级、面向对象的编程语言[6]。通过Objective-C编译的Fry法应变测量程序,可以直接在Objective-C平台上实现Fry图解,使地质人员在野外工作时,利用手机就可以完成原本需要电脑完成的工作,大大的减少了时间成本,且不受地点的限制。
Objective-C和其他编程语言和工具不同,由于它的动态运行时分配性质,它具有一些灵巧的特性和行为,有些功能可以在Objective-C中实现,但无法再其他语言中实现[7]。此外,Objective-C自身具有运行速度快、可读性好、运行环境良好等优点,成为了本次程序编写语言的首选。
2.2 核心算法
(1)在程序输入N个点的坐标之后,自动将这N个点编号为点1、2、3……N,称为原始点;那么原始点的坐标值分别对应为(X1,Y1)、(X2,Y2)、(X3,Y3)……(XN,YN),称为原始坐标。
(2)首先将原始点1(X1,Y1)作为坐标原点(0,0),此时点1的坐标变为(0,0),变化的数值为(ΔX1,ΔY1),那么其余的原始点,即点2至N的坐标依次变为(X2-ΔX1,Y2-ΔY1)、(X3-ΔX1,Y3-ΔY1)……(XN-ΔX2,YN-ΔY2),这样便得到第一组坐标并记录下,坐标数量共有N-1个;再将原始点2(X2,Y2)作为坐标原点(0,0),则第二次变化的数值为(ΔX2,ΔY2)那么其余原始点1、3、4……N的坐标依次变为(X1-ΔX2,Y1-ΔY2)、(X3-ΔX2,Y3-ΔY2)、(X4-ΔX2,Y4-ΔY2)……(XN-ΔX2,YN-ΔY2),这样又得到了一组坐标,称为第二组坐标并记录,坐标数量共有N-1个;重复上述步骤,直到将点1至点N全部循环一次。
(3)通过第二步,一共可以得到N组坐标,共计N*(N-1)个点(不含原点),将这所有点全部投影到一张画布上,便可以得到空白区域为椭圆的Fry图解。
2.3 程序核心代码

3 运用Objective-C实现Fry法应变测量(图解)
3.1 中心点坐标的赋值
先按上述方法岩石各个颗粒(标志体)中心点进行标定,然后把绘有相对位置的透明纸放置到米格纸上,以任一位置为坐标原点(坐标原点的选取必须要使所有点落到第一象限内),将点1、2、3……N的坐标读出。
3.2 输入及运行
打开程序进入输入界面,将在上个步骤得到的点1、2、3……N的坐标依次输入到程序中相应的地方并运行。
3.3 结果与保存
程序运行将会得到有限应变Fry图解,将其保存到移动设备内,再做其他计算。

图3 输入界面图Fig.3 The input interface

图4 Fry图解Fig.4 Fry illustration
4 实例对比分析
本次实例对比分析主要借鉴了韩阳光,颜丹平,李政林对龙门山前陆逆冲构造带泥盆系石英砂岩薄片中变形石英颗粒所做的基于CorelDraw平台进行的Fry法有限应变测量,通过与运用Objective-C做出来的有限应变Fry图解、有限应变椭圆长轴dmax、短轴dmin和轴比R以及应变椭球主轴方位α的对比,做出精确度分析。
4.1 Fry图解对比

图5 石英砂岩的有限应变Fry图解对比图(左图据本文作者,右图据韩阳光,2015)Fig.5 Contrast figure of finite strain Fry illustration of quartz sandstone
4.2 轴比对比
根据轴比公式:
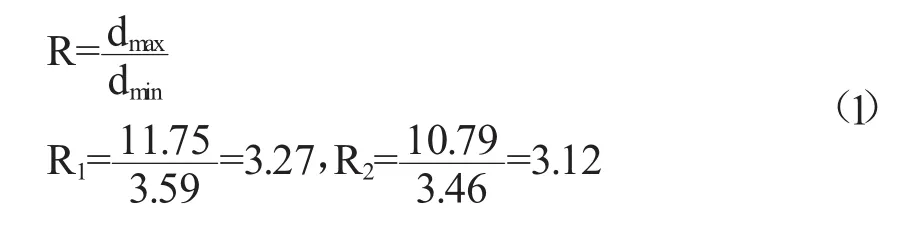
从有限应变图解的椭圆轴比R以及应变椭球主轴方位α的对比分析可知,运用Objective-C的Fry有限应变测量与前人所做的结果基本相同,因此这种算法是可信的,可以用于有限应变测量。但与图4相比,本例的椭圆空白区域边缘未见密集点分布,其原因在于本例的原始岩石颗粒大小不均一,但并不影响二维应变测量[8]。
5 结论
(1)Fry法作出来的有限应变图解是关于中心点(原点)呈现中心对称的。经过Fry法应变测量计算得到的坐标点两两互为相反数,即通过映射在画布上的坐标点的图形关于原点(0,0)呈现中心对称。可以凭借这个特性来检测Fry法图解是否正确。
(2)运用Objective-C的Fry法应变测量其优点有:①与传统的手工Fry应变测量相比,节省了大量的时间,可以大大的提高工作效率。②与基于其他平台的Fry有限应变测量相比,可以在手机上完成Fry图解,此法更为便捷。
(3)二维应变测定的精度主要取决于所测方法假设条件、特别是有关标志体原始状态的假设条件的满足程度[9]。为了提高基于Objective-C的Fry有限应变测量的精确度,我们在标定时,其中心最好位于几何中心,其数量以≥50个为佳;此外未发生形变的岩石通过Fry图解出来的空白区域是圆形。

