游戏化数学学习困难诊断方法及其应用

陈志翰 邱飞岳

摘要：本文通过在线认知游戏训练平台，收集了389名小学四至六年级学生的认知数据，并结合能力差异模型对其进行数学学习困难诊断，最后采用WEKA模型性能分析工具评价该诊断方法的准确性，最终得出结论，即游戏化数学学习困难诊断方法可以较为快速准确地诊断数学学习困难。针对不同年级数学学习内容调整认知游戏的选择方案将有助于提高诊断准确率，同时该方法也为其他学习困难诊断提供了一种新思路。

关键词：数学学习困难；诊断方法；认知游戏；WEKA

中图分类号：G434 文献标识码：A 论文编号：1674-2117（2018）19-0095-04

引言

数学学习困难（以下简称“数学困难”）是学习困难的一个亚型，是指学生智力正常，但是数学成绩明显低于其年龄、智力水平和教育程度应有水平的现象[1]，其发生率约为6%～7%。[2]由于马太效应，数学困难学生的数学成绩将长期处于落后水平，严重影响其学习动机和学业发展[3]，因此，快速准确的数学困难诊断对数学困难学生的学业发展有重要意义。国内外常用一些考察数学基本技能和与数学技能相关认知能力的评估量表来进行早期数学困难筛查[4]，但是传统的纸笔测验和简单纯粹的上机测试难以激发学生的动机，这将导致测试中反映出的能力水平与其实际水平存在显著差异[5，6]，影响测试结果的准确性。借助游戏在激发个体内部动机方面的天然优势，研究人员开发出各种认知游戏用于替代传统的测试任务。这些游戏在维持被试较高内部动机的同时，还能准确地反映被试的能力水平。[7-10]但使用这些游戏数据能否准确诊断数学困难尚待探索。本文拟以广泛应用于临床和教育中的能力差异模型的诊断结果为标准，评价游戏化数学学习困难诊断方法在大范围数学困难诊断中的有效性，为其他类型的学习困难诊断探索有效方法。

对象与方法

1.对象

本研究选取杭州市某小学四至六年级全体学生共389人作为实验对象，其中四年级学生127人（男生68人、女生59人），五年级学生105人（男生50人、女生55人），六年级学生157人（男生93人、女生64人）。被试筛选条件包括：①视力听力正常，并可以独立操作电脑；②可以按照主试的要求并做出相应的反馈；③在实验前均已仔细了解实验目的和实验过程，并签署知情同意书；④前两个学期无转学情况，各项考试数据完整；⑤经《瑞文标准推理测验》测试智力正常。

2.方法

（1）在线认知游戏设计

研究所使用的在线认知游戏均来自Cogdaily在线认知训练平台。该平台目前共有17款认知游戏，涉及工作记忆、加工速度、问题解决能力、注意力和任务切换能力等认知能力。本研究选取了其中7个游戏，分别考察被试的心理旋转、多任务处理能力、加工速度、任务切换能力、选择性注意、视空间工作记忆和工作记忆容量。

在线认知游戏在传统实验任务的基础上加入了以下游戏元素[11]：①在界面显眼位置显示不断减少的游戏时间（除记忆类游戏外），造成紧迫感；②每次操作都会为被试提供反馈，即显示被试的操作是否正确；③随着操作正确率等指标的变化，每次操作的奖励分数也在不断变化，并将总得分实时显示在界面的显眼位置；④根据被试操作情况实时调整游戏难度，同时在调整难度时，注意将难度提高的速度设置得比降低难度的速度慢，以利于游戏更快达到合适的难度并让被试时刻感到挑战性；⑤游戏结束后对游戏得分和排名情况进行显示；⑥游戏的界面和元素都有统一的美工风格，不同游戏会有不同的设计主题。

该平台部署在被试日常上课的机房中，每个被试都独立操作一台计算机，并使用预先分配的实验账号登录平台进行操作。平台将记录下被试在游戏中的每一次操作信息，用于计算反应时间、正确率等指标，并在游戏结束后随游戏得分一起回传到服务器。

（2）数学困难学生标记

从被试所在学校的教务系统中收集被试近两个学期的数学考试，每个学期有六个等级制分数。分数共三个等级，将这三个等级从高到低转化为绩点，并分别取值3分、2分、1分，同时将6个成绩的绩点相加，作为被试该学期的最终数学成绩，以此方法得到每个被试最近两个学期的数学成绩。另外由各班任课教师对学生数学能力进行主观评定，选择近两个学期数学成绩均位于年级后25%[12，13]且同时被教师评定为数学学习困难的49名学生标记为数学困难学生，其中男生29人、女生20人；选择近两个学期数学成绩全优即两个学期的总分均为18分的146名学生作为正常学生，其中男生79人、女生67人。

（3）在线认知游戏数据采集与处理

①安排被试以班级为单位，进入机房进行游戏数据采集。采集过程由1名主试主持，同时配有3名工作人员负责解决被试可能遇到的操作性问题并维持纪律，同时进行采集的被试不超过40人。被试使用预先分配好的账号进行登录，并在主试的指导讲解下逐一进入各个游戏。

②从认知训练平台数据库导出所有被试的游戏数据。由于在数据采集过程中发现存在被试第一次玩某个游戏时未正确理解游戏规则，导致得分异常的情况，但是经过工作人员再次讲解后得分正常，所以在考虑该年龄段学生的认知能力和一般游戏得分范围后，剔除低于500，即在游戏中正确判断不到3次的得分数据。然后选择被试在所有游戏中的第一条数据作为其在该游戏的表现。

③游戏数据的标准化处理。除游戲总分外，与加工速度和注意力相关的游戏数据中还包含平均反应时间、有效操作次数和操作准确率等数据，与记忆能力相关的游戏中还包含最大正确个数、完成率等信息。不同游戏数据因为游戏形式和数值计算方法的不同，取值区间可能有较大差异，这种差异可能导致预测中某些较小分数区间的游戏数据被掩盖。为了消除这种影响，对所有的游戏数据进行组内标准化处理，将所有维度的分数都转换到相同的区间。

以被试ID为关键字段，将每个被试的所有游戏数据共29个维度连同数值化处理后被试的“性别”“年龄”汇总成一条数据，并按照能力差异模型的诊断结果为被试添加“数学表现”字段。

（4）数学困难诊断模型的建立与检验

数学困难的诊断本质上是一个分类问题，本研究使用新西兰怀卡托大学开发的WEKA（Waikato Environment for Knowledge Analysis）作为建立模型和分析模型性能的工具。该工具可以使用已經标记好类别的数据集建立训练模型，并验证模型性能。将数据集导入WEKA后，使用SMOTE（Synthetic Minority Over-sampling Technique）过滤器[14]和LinearNNSearch最近邻搜索算法构建K近邻分类器模型，选择使用十折交叉验证并点击开始。WEKA将自动把标记好的数据集平均分为十份，并将每一份轮流作为测试集、剩余部分作为训练集对模型进行训练和验证，重复10次，得到最优模型并输出分类结果。

3.结果

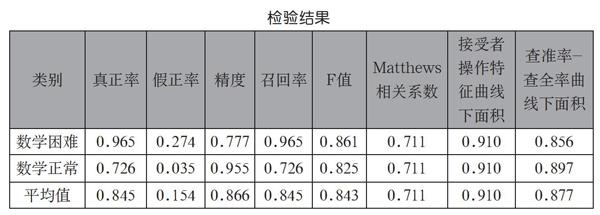
以能力差异模型的诊断结果为标准，游戏化数学困难诊断模型的准确率如下表所示。其中数学困难组真正率为0.965，表示数学困难组96.5%的学生被正确分类，精度为0.777，这表示被诊断为数学困难组的学生中77.7%确实为数学困难；数学正常组真正率为0.726，表示72.6%的正常学生被正确分类，精度为0.955，表示被诊断为数学困难组的学生中95.5%为数学正常学生。从整体来看，84.5%的学生被正确分类，接受者操作特征曲线下面积为0.910，大于0.9，表示模型诊断结果有较高的准确度。

4.讨论

从多元方差分析的结果可以看出，大部分认知游戏的数据都可以很好地区分两组学生，说明认知游戏确实可以用于诊断数学困难，然而两组在与工作记忆能力相关的数据上却差异不大，这与一些研究的结果并不相符。究其原因，其一可能与实验中所使用的游戏的内容有关。实验中采用的工作记忆容量游戏要求被试尽可能多地记住自己选择过的图案，而根据王恩国等人[15]的研究结果，数学困难学生的工作记忆缺陷主要在于数字工作记忆的不足，这可能导致数学困难学生与正常学生在与图案相关的任务表现上并不会出现显著差异。另外，不同的视空间工作记忆成分对不同类型的数学问题解决的影响是不同的，实验中的视空间工作记忆游戏要求被试记住界面中所有点亮的方块，主要考察被动同时性视空间工作记忆。被动同时性视空间工作记忆是心算能力的显著预测变量[16]，而心算能力属于较为基础的数学能力，并不属于四到六年级数学课程考查的范围，所以在该群体的数学困难预测中作用并不大。其二可能与该被试群体的工作记忆水平有关。四到六年级的学生工作记忆能力尚属于发展期，虽然工作记忆能力可以影响个体的数学表现，但是在该群体中工作记忆水平的个体差异不明显，所以并不能作为该群体数学表现的预测因子。故在选择认知游戏的种类时，需要考虑到不同年级学习内容的差异，详细区分不同知识点对各认知能力的需求。

从诊断结果来看，游戏化数学学习困难诊断方法的结果与基于能力差异模型的诊断结果相似度较高，说明游戏化的诊断方法具有较高的准确性。其中几乎所有的数学困难学生都被正确诊断出来，同时也有很小一部分的正常学生被错误诊断为数学困难。这一现象在分类问题中时有发生，在本研究中，主要原因可能与学生成绩为等级制有关。等级制分数降低了学生之间的差异性，只有成绩极为落后的学生才被评为最低等级，而大部分学生成绩都是优秀，导致全优的学生过多，正常组学生的数据特征不够明显。这一现象也说明本研究提出的诊断方法对于数学困难学生更为敏感，在数学困难诊断中，尽可能找到所有数学困难学生显然也更加重要。

结语

本研究提出的游戏化数学学习困难诊断方法可以较为准确地诊断数学学习困难，有望为其他类型的学习困难诊断提供一个新的方法。受限于研究样本数量和认知游戏种类，仍有一小部分正常学生被误判为数学困难学生。在后续研究中仍需扩大数据采集范围，合理选择游戏种类，提高诊断的准确性。

参考文献：

[1]Geary D C. Mathematical Disabilities-Cognitive， Neuropsychological， and Genetic Components[J].Psychological Bulletin，1993（2）：345-362.

[2]Geary D C， Hamson C O， Hoard M K. Numerical and arithmetical cognition： A longitudinal study of process and concept deficits in children with learning disability[J].Journal of Experimental Child Psychology，2000（3）：236-263.

[3]Bull R， Espy SA K. Short-term memory， working memory， and executive functioning in preschoolers： longitudinal predictors of mathematical achievement at age 7 years[J].Developmental Neuropsychology，2008（3）：205-228.

[4]王勇丽，周欣，宿淑华，等.儿童数学学习困难的诊断和评估量表[J].中华行为医学与脑科学杂志，2014（10）：949-952.

[5]Bauer L， O'Bryant S E， Lynch J K， et al. Examining the Test Of Memory Malingering Trial 1 and Word Memory Test Immediate Recognition as screening tools for insufficient effort[J].Assessment，2007（3）：215-222.

[6]Courtney J C， Dinkins J P. Age related effects in children taking the computerized assessment of response bias and word memory test[J].Child Neuropsychology，2003（2）：109-116.

[7]McPherson J， Burns N R. Assessing the validity of computer-game-like tests of processing speed and working memory[J]. Behavior Research Methods，2008（4）：969-981.

[8]Angeles Quiroga M， Escorial S， Roman F J， et al. Can we reliably measure the general factor of intelligence （g） through commercial video games？ Yes， we can！ [J].Intelligence，2015（8）：1-7.

[9]MF. Rosetti， MF. Gómez-Tello， Victoria G， et al. A video game for the neuropsychological screening of children[J]. Entertainment Computing，2017（5）：1-9.

[10]Tenorio Delgado M， Arango Uribe P， Aparicio Alonso A， et al. TENI： A comprehensive battery for cognitive assessment based on games and technology[J].Child Neuropsychology，2016（3）：276-291.

[11]Landers R. An Introduction to Game-based Assessment： Frameworks for the Measurement of Knowledge， Skills， Abilities and Other Human Characteristics using Behaviors Observed within Videogames，2015.

[12]Fuchs L S， Fuchs D， Prentice K. Responsiveness to mathematical problem-solving instruction： comparing students at risk of mathematics disability with and without risk of reading disability[J].Journal of Learning Disabilities，2004（4）：293-306.

[13]Zheng X， Flynn L J， Swanson H L. Experimental Intervention Studies on Word Problem Solving and Math Disabilities： A Selective Analysis of the Literature[J].Learning Disability Quarterly，2013（5）：97-111.

[14]曾志強，吴群，廖备水，等.一种基于核SMOTE的非平衡数据集分类方法[J].电子学报，2009（11）：2489-2495.

[15]王恩国， 刘昌， 赵国祥.数学学习困难儿童的加工速度与工作记忆[J].心理科学，2008（4）：856-860+847.

[16]朱晓斌，王静丽，李晓芳.视空间工作记忆和非言语流体智力在小学生数学问题解题中的作用[J].心理科学，2011（4）：845-851.