静止轨道遥感卫星标称网格及其生成方法探讨

丁 璐,秦志远,童晓冲,赖广陵

(1. 战略支援部队信息工程大学,河南 郑州 450000;2. 河南城建学院,河南 平顶山 467036)

0 引 言

静止轨道遥感卫星属于高轨卫星,相对地球处于静止状态,该卫星具有"站得高,看得远"的特点,可以实现对目标的持续、动态观测.尤其是近几年,美国GOES-R[1]、日本"葵花9号"[2-3]、我国"高分四号"[4-5]和"风云四号01星"[6-8]等新一代国内外静止轨道遥感卫星陆续发展,欧洲的MTG系列I星也计划于2018年发射升空[9],静止轨道遥感卫星应用将变得越来越普遍.在静止轨道遥感数据的应用与发布过程中,标称数据是其中最主要的数据形式,如我国风云二号的L1A级数据[10]以及美国GOES-R卫星的L1B级数据[11]等都是采用的标称数据发布.对于标称数据而言,标称网格的定义与生成是其关键性的内容,标称数据就是利用标称网格重采并承载发布的数据,是根据卫星成像特点、投影方式,结合轨道姿态星历等基本数据,经过计算得到的基础数据,包括每一个标称网格点对应的影像灰度值、定位结果(经纬度坐标)、卫星方位角等内容,可以为后续静止轨道遥感卫星各级产品的生成提供支撑,具有十分重要的现实意义.

目前,国内外静止轨道遥感卫星的成像方式主要有两种:一种是画幅式成像,即采用面阵CCD/CMOS对某区域进行一次性成像,成像投影方式采用的是面阵中心投影的方法,如高分四号的对地成像[12];第二种是扫描镜成像,为了快速获取大面积的遥感数据,特别是地球完整圆盘数据,常采用线阵扫描成像方式,利用东西、南北两个方向的快速扫描与步进完成大幅面区域的覆盖[13],这种成像方式采用的是规范化地球静止投影(Normalized Geostationary Projection,NGP)[14-16],并且这种投影还会因光线进入东西、南北两个扫描镜的顺序不同而有所差异.因此,需根据卫星的成像特点,选择恰当的投影方式,形成作为参考基准的标称网格数据.本文根据成像方式,就现阶段两类3种标称网格数据的生成方法进行了探讨,给出了具体的计算过程,并设计实验比较了不同方法之间的差异.论文的研究可以为后续标称网格的选择、生成、转换等提供理论依据,为后续静止轨道遥感卫星产品的生成提供技术支撑,具有十分重要的意义.

1 标称网格的生成方法

1.1 基本概念

当静止轨道遥感卫星位于预设位置(地球同步轨道上静止),对地指向恒定为零,姿态角为零,相对于地球静止,传感器安装矩阵理想,系统光路无任何变形的情况下,理想像平面对地扫描成像,按照一定的扫描间隔(东西方向、南北方向),每一条扫描线在地球表面定位点的连线网格被称为标称网格.

以扫描镜成像方式的静止卫星为例,在满足上述基本条件情况下,东西镜按照理想驱动规律扫描、南北镜按照理想驱动规律步进时,根据标称网格的定义可以发现网格的格点是由东西镜、南北镜按照固定角度步长Δα,Δβ进行扫描,获得地面点坐标所构成的.将南北镜、东西镜的旋转角范围进行限定,如α∈[α0,αn-1]、β∈[β0,βm-1],令:

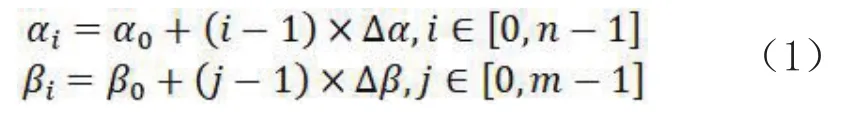
对于每一个旋转角组合(αi,βj),理论上都存在一个(L,B)(i,j)与之对应,可以得到地球表面一个mXn个点的格网.

下面分别对扫描式和画幅式静止轨道遥感两种成像,讨论对应的几种标称网格的计算方法和区别.

1.2 扫描式成像标称网格计算

1.2.1 NGP标称网格

NGP标称网格是世界卫星协调组织(CGMS)采用的NGP投影方式定义的标称网格,目前已经成为气象遥感的国际标准之一,使用最为广泛,美国的GOES-R、日本的H8、中国的风云等气象遥感卫星都采用了该标称网格,本文将其简称为NGP网格,文献[15]中有NGP网格的详细定义.

NGP网格定义了NGP的投影方式,该投影方式是由图中λs和Φs,实际上就是以卫星Satellite为中心,定义了一个极坐标系统.下面给出NGP投影的相关解释,如图1所示.

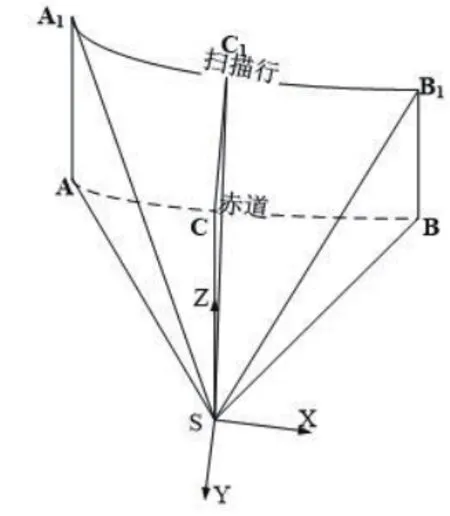
图1 NGP投影的解释Fig.1 Interpretation of the NGP projection

S为Satellite卫星,ACB为赤道,A1C1B1为一条扫描线,其中,C为星下点,A1A⊥ACB,C1C⊥ACB,B1B⊥ACB,A1和A两点的扫描角都为∠ASC,B1和B两点的扫描角都为∠BSC,C1和C两点的扫描角都为0.A1的步进角为∠A1SA,C1的步进角为∠C1SC,B1的步进角为∠B1SB,满足关系

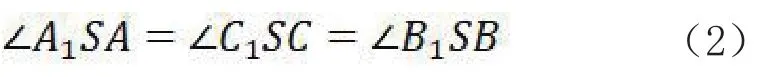
以S为中心,建立直角坐标系S-XYZ,其中SY⊥ACB并向下,SZ指向地心,SX满足右手法则.按照图1的描述,可以非常简单地定义NGP投影,并因此生成NGP网格,设置两个方向的角度λs(东西方向)、Φs(南北方向),图3中的,,,,,就是对应1不同角度的出射光线,对应于东西方向角λs,南北方向角Φs,在S-XYZ坐标系中,光线向量为:

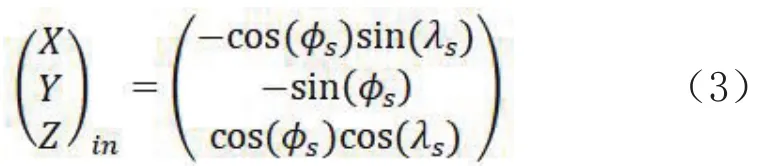
按照固定变化值选择λs和Φs,如λs=λ0+ΔλXn,Φs=Φ0+ΔΦXm时(如式(1)),即可以得到生成NGP网格的所有光线,当这些光线与地球椭球求交后,即可得到NGP的标称网格,如图1所示.需要说明的是,官方的NGP网格生成方式采用的是Mercator投影的方式给出的,是采用投影方程和投影系数得到的结果,并没有使用光线计算的方式.当然,投影系数方程的方式用户使用简单不需要了解原理,但其过程是由光线推导出来的.

上文就NGP网格的生成方式进行了简单的叙述,下面从扫描成像的角度,就NGP网格以及对应的NGP投影对应的扫描方式进行分析,如图2所示,该图描述的就是一种采用东西、南北两个方向扫描镜的光机扫描方式.

图2 NGP投影对应的成像扫描方式Fig.2 Corresponding imaging scanning mode of NGP projection

图2 定义了相关坐标系统,包括卫星的本体系、探测器的载荷系,用于东西、南北两个方向扫描的扫描镜坐标系,考虑理想状态,其坐标轴方向都保持平行.光线随着两个扫描镜转角的变化而进行变化,定义南北镜子转角为α,东西镜转角为β.其中,α=0,β=0时,南北(东西)镜镜面法向分别在南北(东西)镜坐标系下的坐标为:

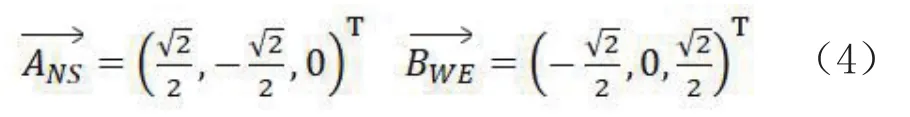
在图2中载荷安装矩阵为单位阵的情况下,载荷坐标系示意图如图1所示,假设载荷坐标系中的出射视向量为(X1,Y1,Z1),经过两次光线反射之后的视向量L,即出射光线为:

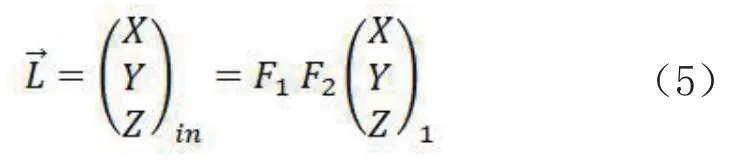
式中,F1、F2分别为南北、东西镜的反射矩阵,由南北、东西镜法线ANS、BWE及南北镜的转角α、东西镜的转角β构成,分别如式(6)和(7)所示:

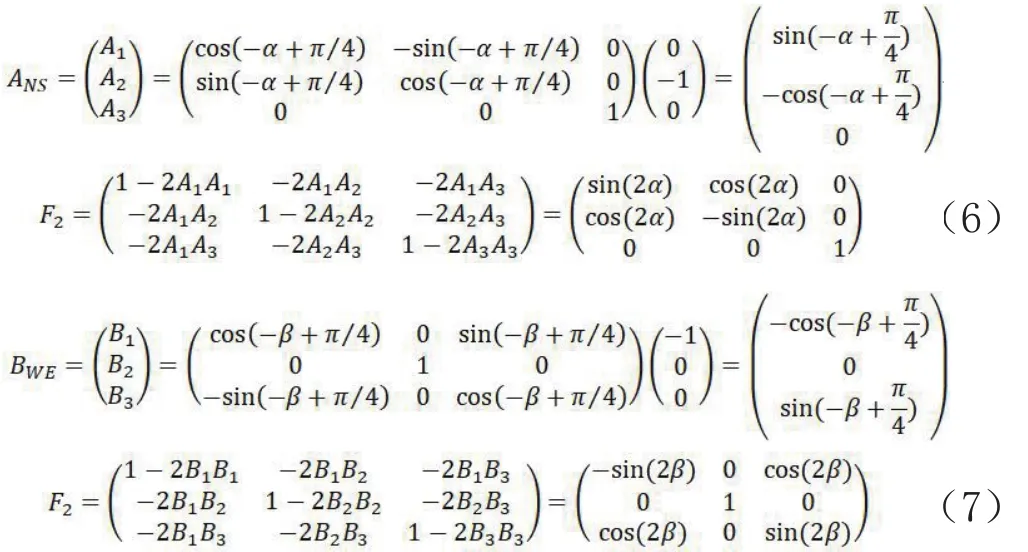
将式(6)、(7)代入是(5),可以得到:

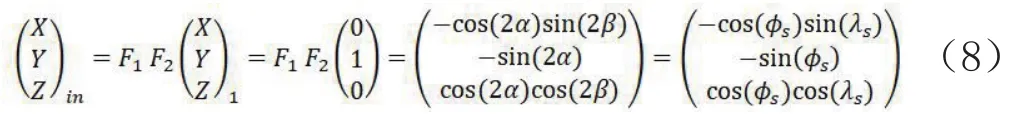
将式(8)与式(3)对比,就可以发现,两者的形式是相通的,只需要保证镜子扫描角和NGP投影中光线夹角的关系保证:2α=Φs,2β=λs即可.因此,可以确定的是,图4的扫描方式对应的就是NGP投影的NGP标称网格.

实际上,在标称网格生成的过程中,还需要经过一系列的坐标转换,将本体系出射的光线通过卫星轨道坐标系(标称位置)、地固坐标系(标称状态不考虑惯性坐标系的问题)、大地坐标系等一系列转换[17],最终才能得到最终的地表标称格,但是这些后续的转换在所有标称格计算中都是一致的,各种标称格之间差异的核心在于卫星本体坐标系下出射光线的差异,因此,下面的对比研究仅对出射光线进行讨论.

1.2.2 NNGP标称网格

上一节中,证明了图2的扫描成像方式就是CGMS定义的NGP投影,目前,美国的GOES-R、日本的Himawari8采用的都是这种成像光路.分析这种光路可以发现,光线进入南北镜、东西镜的顺序的不同也会导致成像光路的差异,其定义与图2相似,只是光线进入扫描镜的顺序有所差异.采用类似的推导方式,可以得到另一种形式的成像光路,如公式(9)、(10)所示:

经过上述坐标转换关系即可得到射入像空间坐标系的光线坐标,入射光线,因此,出射光线满足:

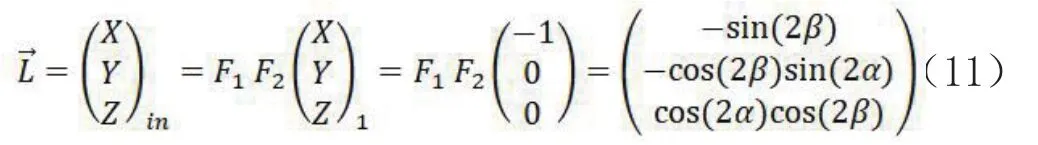
上面文章叙述了扫描式成像中标称网格的基本方式,对于像平面上的每一个点,经过一系列坐标转换之后可以得到相应的地面点的经纬度坐标,这些坐标的分布是不规则的,因此标称网格的生成需要建立标称格的行列编号(I, J)与地面点(B, L)之间的关系.需要说明的是,在标称格生成的过程中,除了这样的正算过程,即(I, J)→(B, L)的过程;而另一个过程,即已知地面(B,L)来反查标称网格(I, J)的过程也是比较常用的.对于扫描型的标称网格的反算过程,实际上也比较简单,基本思路是将卫星位置连接地面点(B, L)的连线单位化后,通过坐标转换到理想状态的本体系中,其结果应该是与式(8)或(11)中的光线向量相等的,由此计算对应的镜子转角α和β,通过转角与初始位置的关系,以及每次转角步进值,即可计算对应的行列号(I, J).

1.3 画幅式成像标称网格计算

第二种成像方式就是画幅式成像,传感器采用画幅式相机一次性地获取图像.虽然,画幅式成像由于成像幅面等技术问题,不可能做得很大,直接用其进行整个地球圆盘的拍摄时,需要多次成像,效率较低.但是由于他的稳定性和便捷性,如果用于局部区域跟踪或者快速成像等工作,将具有较大的潜力,我国的高分四号卫星等采用的就是画幅式静止轨道成像方式[18],该成像方式采用的是椭球外心透视方位投影的方法[19].下面针对这种成像投影方式,分析其可能的标称网格计算方法.图3是画幅式理想情况下扫描示意图.

图3 画幅式理想情况下扫描示意图Fig.3 Scanning schematic diagram of the ideal picture type

由于画幅式是瞬间成像,因此并不等同于扫描成像的方式,从图3中可以发现,画幅式成像的最大几何特点是两个基本的共面条件加上一个夹角条件,即:①任意一行标称格(行号相同)所对应的所有光线共面;②任意一列标称格(列号相同)所对应的所有光线共面;③相邻行号、列号形成的面与面之间的夹角相等,等于像元张角.这和扫描成像的方式对比,具有很大的区别,从式(8)和(11)可以发现,对于扫描成像的传感器而言,不管是采用哪种标称网格(NGP标称网格或NNGP标称网格),其出射光线均受镜子转角的影响,无论如何都不能满足这两个基本的共面条件,这也是两大类标称网格最大的区别.下面就利用这两个基本的共面条件来计算画幅式成像标称网格.

1.3.1 正算方法

已知:如图3所示,S-XYZ为轨道坐标系,卫星的标称位置S,理想情况下(轨道、姿态标称),地球是参考椭球⊙O,采用画幅式扫描形成标称网格,网格大小mXn,每个网格对应的像元张角为Δθ.

计算:标称网格上行列号分别为(I, J)的网格,对应的大地经纬度(B, L).

基本思想:任意一行标称格(行号相同)所对应的所有光线共面,所有行可以形成m个相交平面Fi(i=0,1,…,m-1);任意一列(列号相同)标称格所对应的所有光线共面,所有列可以形成n个相交平面Ei(i=0,1,…,n-1).行列号分别为(I, J)的网格P(I, J)满足:

那么求解标称网格上点的过程,采用式(12)的思路来完成,核心是Fi和Ej的计算,下面给出具体步骤.

1)根据(I, J)值,计算Fi和Ej,由于相邻行号、列号形成的面与面之间的夹角相等,等于像元张角Δθ,由于(I, J)是从网格的左上角点记录的,星下点D对应的是半个网格的位置,即4个网格点中心,因此,Fi面与赤道面(面SOF)的夹角Φi,Ej面与面SON的夹角Ψj分别为:

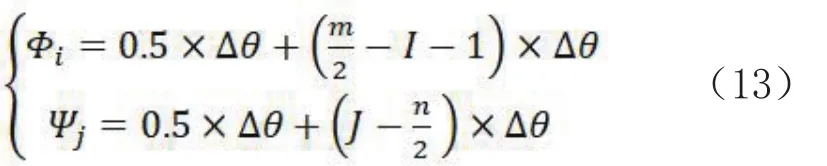
2)Fi面由面SOF绕S-X轴旋转Φi得到,Ej面由面SON绕S-Y轴旋转Ψj得到;

3)计算面Fi∩面Ej=Lij,得到交线,计算Lij∩⊙O得到行列号为(I, J)的标称格坐标(B, L).

1.3.2 反算方法

画幅式成像标称网格的反算方法与扫描式的差距较大,下面给出反算的步骤,仍然以图3来说明问题,以A点来计算对应的标称网格(I, J),具体步骤如下:

1)以ND为对称轴,计算A点在⊙O上的对称点B,面ASB∩⊙O=AB,AB∩ND=E;以赤道为对称轴,计算A点在⊙O上的对称点C,面ASC∩⊙O=AC,AC∩赤道=F,满足下面关系:

A点的扫描角=F点的扫描角;A点的步进角=B点的步进角

2)需要计算E点的纬度和F点的经度,即计算图3中的λ、Φ,然后根据λ和Φ来计算A点的扫描角和步进角,不能直接使用A点对应的经纬度来计算.下面给出E、F的计算方法:

3)在沿着赤道的截平面(如图4a所示)中,计算β=∠OSF,根据余弦定理

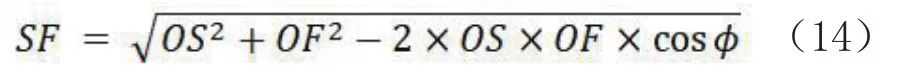
式中,OS=OD+SD=a+H,地球的长半轴为a,OF=OD=a,H为卫星的标称高度.根据正弦定理:

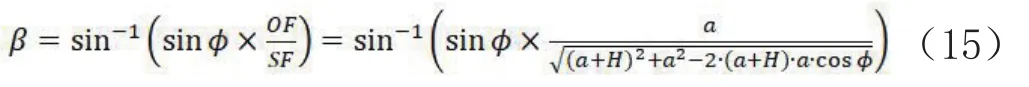
图4 不同方向的截平图Fig.4 Cross-sectional plan of diあerent directions

OE、OS、∠EOS已知,按照上面类似的方法可以计算角α,注意OE的大小是用E的地固坐标计算的,OS=H+a.

5)根据α和β计算I、J

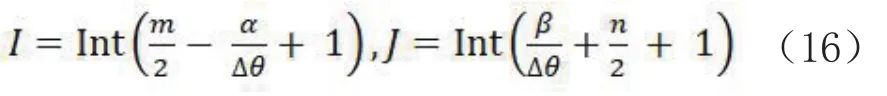
式中,mXn为标称格的大小,Δθ为该波段像元的微弧数.

2 实验与分析

论文给出了两类3种标称网格的生成方法,本节设计了相关实验来说明.下面给出一些基础的实验数据及条件:

1)静止轨道卫星标称位置:星下点(104.7°,0°),标称高度H=35 786km;

2)地球椭球长半轴a=6378.137 km,短半轴b=6356.752 km;

3)生成星下点分辨率为ρ=500 m标称网格;

4)标称网格的尺寸按照CGMS约定的22 000X22000;

5)对比NGP网格、NNGP网格、画幅式成像网格3种标称网格.

根据星下点分辨率计算对应的每个网格对应的像元张角Δθ,有:

3种类型标称格的差异,由于尺寸较大,需要每隔若干点采集1个点进行比较,另外无论标称网格的分辨率如何变化,影响坐标的实际上是投影方式,即本文涉及的计算方法,因此以分辨率为500m标称格为例说明问题,其他分辨率的规律类似,实验对比:

1)正算对比:计算同样的I、J下转换成B、L的差异,在22000X22000的标称格上,选择100X100个均匀格点进行对比,分别对比3种标称格正算过程中B、L的差异;

2)反算对比:计算同样的B、L下转换成I、J的差异,由于(B,L)无法规范化地得到,因此先利用NGP网格定位后的(B,L)按照100X100个均匀选点,3种标称格方法反算得到标称格行列号,分别对比3种网格反算过程中I、J的差异.

图5是3种标称网格正算过程中,定位经纬度的差异,100X100个网格点阵,按照先行(经度)、后列(纬度)顺序排列的效果,由于量纲是度,因此效果不明显,只能看出整体差异;图6是图5中第10、30、50行单独取出的情况,效果更加清晰,大于50行的对比,从图5看来,与小于50行是对称的;另外,由于标称网格是经度、纬度两个方向分布的,前面的结果是按照行来看的,只能了解经度方向的变化,我们还绘制了纬度方向的差异,由于篇幅原因图略.图7是3种标称网格反算的对比,100X100个网格点阵,相同经纬度(B,L)反算标称格(I,J)比较,由于行列号可以看出差异,因此直接采用了二维显示的方式,并且选择了3个区域进行放大对比;论文实验还仿照正算的情况,给出了单独行、列方向的反算对比的情况,由于篇幅所限,图略.

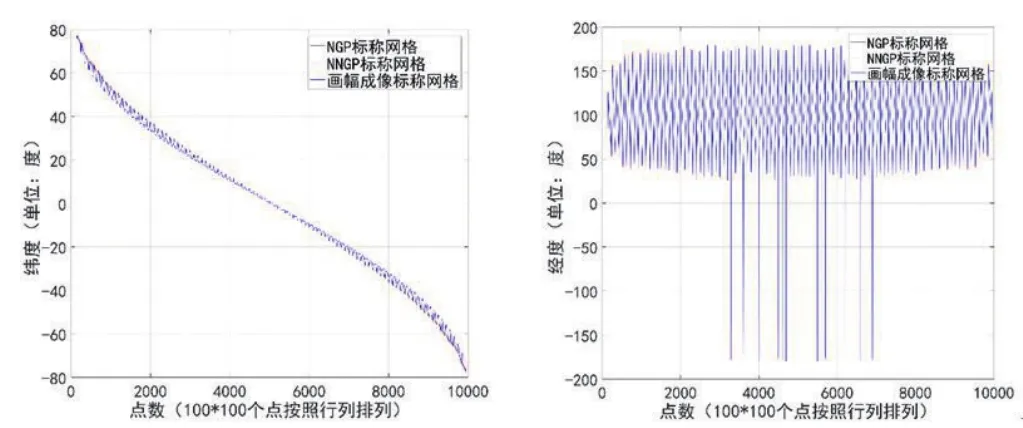
图5 3种标称网格定位经纬度差异,100X100个网格点阵,按照行列顺序排列Fig.5 Diあerences of location latitude and longitude of three kinds of nominal grid,100X100 lattice grid,arranged by row and column

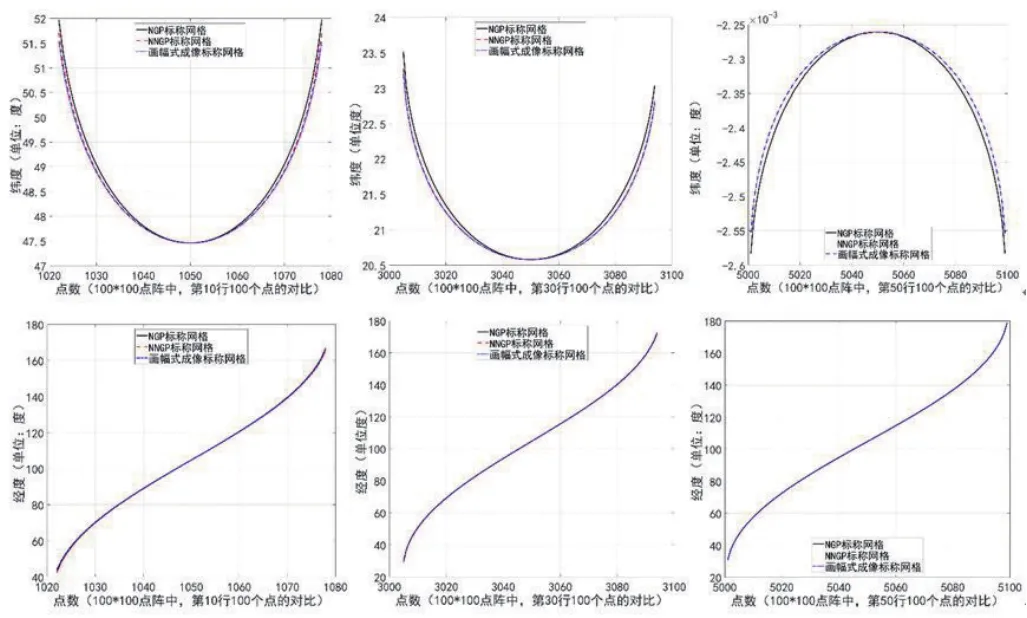
图6 3种标称网格定位经纬度差异,100X100个网格点阵中第10、30、50行的情况Fig.6 Diあerences of location latitude and longitude of three kinds of nominal grid,situation of the 10th, 30th,50th row of 100X100 lattice grid

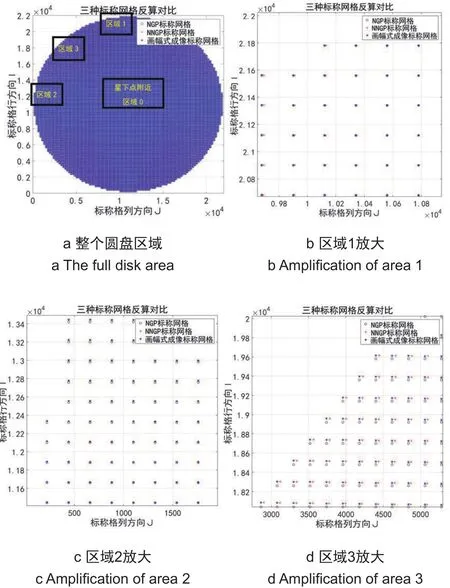
图7 3种标称网格反算对比,100X100个网格点阵,相同经纬度(B,L)反算标称格(I,J)对比Fig.7 Comparison of back calculation of three kinds of nominal grid,100X100 lattice grid, comparison of back calculate nominal grid(I,J)in same latitude and longitude(B,L)

从上述实验结果,结合图7a地球圆盘上,不同区域的划分示意图,可以得到下面几个方面的结论:

1)3种标称网格计算方法,得到的标称网格坐标整体趋势是吻合的,但是两两之间都存在一定差异,从整体规律来看,越接近星下点位置(区域0)的网格差异越小,其他区域差异随着离开星下点位置越远,差异越大,但是规律各不相同;

2)网格正算过程,在行方向上存在以下规律:

①随着行数的增加,3种标称网格计算的纬度B差异是在逐渐变小,到中间一行最小,然后又逐渐变大;

②同一行内,NGP网格纬度B>NNGP网格纬度B>画幅式成像网格纬度B;其中最大差异,NGP网格与NNGP网格有0.27°左右,相当于地面上30km;NGP网格与画幅式成像网格有0.44°左右,相当于地面上49km;

③在赤道处,NNGP网格纬度B=画幅式成像网格纬度B,NGP网格纬度B与其他两种的差异最大在区域2的位置,量级在(3X10-5)°左右,相当于地面上3.3 m;

④同一行内,3种网格经度L的变化有所区别,以中央经线为对称点,在中央经线西边,NGP网格经度L>画幅式成像网格经度L>NNGP网格经度L;在中央经线东边,NGP网格经度L<画幅式成像网格经度L

⑤在赤道附近,NNGP网格纬度L=画幅式成像网格纬度L,NGP网格与两者差异最大在区域2的位置,量级在(1.5X10-3)°左右,相当于地面上167m.

总体而言,在整体行方向,NGP网格与NNGP网格更加接近;越来越接近赤道的位置,NNGP网格与画幅式成像网格趋于一致.

3)网格正算过程,在列方向上存在以下规律:

①列方向的规律和行方向的规律正好对应,按照旋转90°来看,经纬度的规律相反,其中经度方向呈现NGP网格纬度L>NNGP网格纬度L>画幅式成像网格纬度L,在中央经处,NGP网格纬度L=画幅式成像网格纬度L;

②列方向纬度最大差异,NGP网格与NNGP网格有0.26°左右,相当于地面上30km,但是需要注意的是,两者的差异最大不是最小列和最大列,而是中间部分的第30列;纬度方向,NGP网格与画幅式成像网格,最大差异有3°左右,相当于地面上334 km,同样最大值也是中间部分的第30列;

③纬度方向上,呈现出以赤道为对称轴的对称关系,在赤道北边,NGP网格纬度B>NNGP网格纬度B>画幅式成像网格纬度B;在赤道南边,NGP网格纬度B

④经度方向上,NGP网格与NNGP网格随着越来越接近中央经线,差异越来越小;而NGP网格与画幅式成像网格,是30列左右反而差异最大;

总体而言,从列方向来看,NGP网格与NNGP网格更加接近,但是在列方向的主体部分,NNGP网格与画幅式成像网格更加接近,只是在列的边界部分,画幅式成像网格与两者的差异出现了剧烈变化;在中央经线处,画幅式成像网格与NGP网格、NNGP网格趋于一致;

综合(B, L)两个方向,相对于其他区域,区域3的位置,3种网格的定位差异最大,其中,画幅式成像网格的纬度和其他两类网格差异最大,但是需要说明的是,在圆盘主体部分,NGP网格与画幅式成像网格更接近些,但是在圆盘边界部分,画幅式成像网格与其他两类网格的差异出现剧烈变化.画幅式成像网格在赤道处与NNGP网格完全一致,在中央经线处趋于一致;与NGP网格在赤道、中央经线处趋于一致.

4)网格反算过程,从行方向来看具有以下规律:

①反算I坐标的情况,NNGP网格与画幅式成像网格的最大差异只有0.5个网格单元;而NGP网格与其他两种最大差异可以达到40余个网格单元,并且最大差异是在区域3,在赤道处与画幅式成像网格趋于一致;

②反算J坐标的情况,NGP网格与画幅式成像网格一直是相等的,与NNGP网格最大差异是50网格单元左右,随着纬度减少差异逐渐减小;

5)网格反算过程,从列方向来看具有以下规律:

①反算I坐标的情况,NNGP网格与画幅式成像网格的最大差异只有0.4个网格单元;而NGP网格与其他两种最大差异可以达到50个网格单元左右,差异随着越来越接近中央经线而减少,在赤道处与画幅式成像网格趋于一致;

②反算J坐标的情况,NGP网格与画幅式成像网格一直是相等的,而NNGP网格与其他两种最大差异可以达到40多个网格单元,并且最大差异是在区域3.

总体而言,在反算J坐标的情况下,NGP网格与画幅式成像网格是完全一致的,没有差异,NGP网格与NNGP网格之间最大差异位于区域3;在反算I坐标的情况下,NNGP网格与画幅式成像网格是基本一致的,差异不大于0.5个网格单元,而NGP网格与两者的差异最大同样位于区域3.

综上所述,3种标称网格在正算方面,综合(B, L)两个方向,在圆盘区域的内容主体部分,NGP网格与画幅式成像网格更加接近;而在圆盘的边界区域,画幅式成像网格与其他两种网格差异较大,而且基本上是快接近边缘处剧烈变化;按照差异大小排序:区域3>区域1>区域2>区域0.3种标称网格在反算方面,NGP网格与画幅式成像网格更加接近,特别是在J坐标方向,完全一致;NGP网格与两种网格反算过程中,考虑(I, J)两个方向的差异,按照差异大小排序:区域3>区域2>区域1>区域0.

3 结束语

论文针对静止轨道遥感卫星标称网格生成方法进行研究,结合卫星成像原理,给出了NGP标称网格、NNGP标称网格以及画幅式成像标称网格3种标称网格的计算方法.设计了3种方法的正反算对比实验,并对实验结果进行分析,得出了不同标称网格正、反算的区别,以及不同种类标称网格在各区域内的变形与差异,该项研究对于静止轨道遥感卫星标称数据的发布、应用以及不同网格数据的转换等工作都具有十分重要的意义.