一类流数据的抽样及其存储方法研究
王佐仁,徐生霞
(1.西安财经学院 a.统计学院,b.西安统计研究院,陕西 西安 710061; 2.首都经济贸易大学 统计学院,北京 100070)
一、引言
随着信息产业的迅速崛起和发展,大数据时代悄然来临,出现了一种新型的数据——流数据(Data stream)。流数据的定义至今还没有完全统一。按照Henzinger等于1997年首次对流数据的描述和定义[1],后经学者们不断认识和修改,目前流行的定义是:流数据是一组按时空顺序、大量、快速、连续到达的数据序列。一般情况下,流数据可被视为一个随时空延续而无限增长的动态数据集合。流数据具有持续流入、数据量大、数据形式多样、时空变化性强等特点。
关于流数据的研究思路,从统计学的角度看,可以分为两大类,一类是把流数据的全体作为样本数据进行数据处理。如Ajtai等在对流数据初步认识的基础上于2002年提出了基于计数反演算法流数据模型的讨论[2];Babcock等于2002年在探讨流数据模型的查询和算法问题的基础上设定了流数据模型[3];Abadi等人在2003年提出了一种基于哈希算法的管理流数据技术[4]。这些流数据的研究结论,都是在全体数据参与运算的基础上完成的。由于数据量大,和大数据的处理方式一样,其应用需要分布式处理技术、并行计算技术、云计算技术的支持。另一类是把流数据的全体作为总体,通过从总体中随机抽取样本,用样本数据进行数据处理,提炼有用信息。显然,后一种研究思路可以大大节省资源,但增加了流数据的抽样方法研究问题。关于流数据的抽样,王莹、Alon、Balazinska、Cormode、Greenwald等先后于2001年到2005年之间提出了地域抽样、蓄水池抽样、优先抽样等抽样方法[5-9],也将流数据的存储与抽样方法结合起来,但是存在难于提炼流数据特征的局限性。Babcock、Tang等在解决流数据瞬息万变特征的基础上提出了滑动窗口抽样[3][10];Cormode等在考虑流入数据概率不等情形下提出了加权蓄水池抽样[8]。这些抽样方法,都是在流数据数量规模未知,抽样与数据流入同步进行,样本的构成或总体特征等运算是在不断调整参数下即时完成的。固然,这种信息自动生成有着明显的数据处理优势,但没有完整的概率结构,其抽样误差以及各种信息值的精度无法讨论。
流数据来到具有鲜明的随机性,首先是来到的个数具有随机性,其次取值具有随机性。至今,还未发现在随机性的假定条件下,讨论抽样和存储方法的研究成果。本文针对流数据这两个随机性,分别假定其为一般的概率分布,将其纳入到概率空间的轨道上,在不放回抽样条件下,讨论抽样误差和存储方法,无疑具有理论与实践意义。
二、条件分布下流数据的抽样误差
(一)基本假定
在一定的时间区间上,流数据的来到的个数虽然数量之大,但最多也会是有限个。因此,假定流数据来到的个数为有限个,流数据来到的个数服从离散型分布,其取值对应于有序的有限向量。为了方便起见,仅就取值为一维情况进行讨论。

Xt为时间间隔(0,t]上来到的流数据数值Zt的个数,Xt的分布为:
P(Xt=i)=αi(i=1,2,…,N)
其中αi≥0,∑αi=1
(1)
P(Zt1=zt1,Zt2=zt2,…,Ztk=ztkXt=i)
(2)
对zt1,zt2,…,zti∈{z1t,z2t,…,zNt}成立;即在Xt=i发生的条件下,{z1t,z2t,…,zNt}中任何固定的i个数据到来的机会是均等的。
这种假定也有广泛的适应性,如一段时间的打电话人数,某天检查身体的人数,某天外汇兑换的笔数,某段时间股票交易的笔数,某天空气质量监测数据数等。
据条件(1)与(2),可以得到:

Var(Zt)=E(Zt-EZt)2

P(Xt=i)
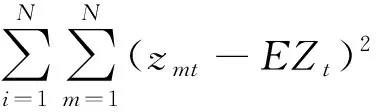
P[Zt=zm t|Xt=i]αi

(二)条件分布下的样本均值与方差

证明:按条件(2)
(3)





证明:按条件(2)






(4)
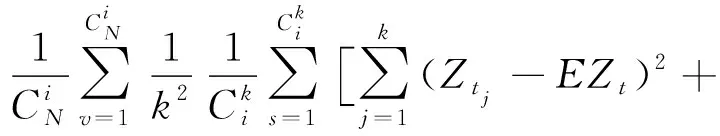




(5)
(6)
将式(5)和式(6)的结果代入式(4)可得:
从定理2可以看出,样本方差与条件分布有关;并且




特别地,当i (7) 证明: (8) 由于 (9) 将式(5)与式(9)代入式(8)就有: 所以, (10) 这些结果说明,在流数据到来个数不确定的情况下,流数据随机到来的个数与样本容量有关,当来到的数据个数小于抽样个数存在时,会带来信息的损失,因而用得到的样本去估计总体均值时,样本均值是总体的有偏估计,但抽样误差相对较小,其样本均值的偏离程度、抽样误差与流数据到来的个数大于样本容量的概率成正比。但当来到的数据个数永远不小于抽样个数时,样本总能抽得,信息量充足,样本均值才是总体均值的无偏估计并且抽样误差与传统抽样误差相同。这些不难从定理3和式(10)看出。 第二节在固定的区间上,对流数据的统计学性质进行了讨论,得出了在流数据来到的个数不小于样本容量时,样本均值为总体均值的无偏估计等结论。这一节我们运用第二节的结论,将固定区间动态化,视为流数据连续到来,讨论样本分批随机抽取、动态存储的方法。为此,设流数据共有k个存储位置,流数据到来的时间区间为(0,+),将(0,+)等间隔分为(tj-1,tj](j=1,2,…,n,…),假定流数据在区间(tj-1,tj]来到的个数Xtj独立同分布,其分布为:P(Xt=i)=αi(i=1,2,…,N),其中αi=0(i 对于区间(0,t1]来到的流数据,按不放回抽样,抽取容量为k的样本,依次存储这k个数据到k个存储位置;对于区间(t1,t2]来到的流数据,按不放回抽样,抽取容量为k的样本,依次用前两次抽到对应位置的数据的算术平均值替代第一次相应位置的存储数据;按照这样的存储方法继续进行,……,设从第n个区间(tn-1,tn]来到的流数据中按照不放回抽样抽取容量为k的样本,依次将前n次来到的对应位置上的样本数据的均值存储到相应的k个存储位置上。 (11) 定理4设Ztj1,Ztj2…Ztjk为第j个区间依次随机抽取的样本数据,对排序在第l(1≤j≤k)个位置的随机数据Ztjl都有: 证明:据定理4及式(6)有: 依据定理5与定理6,可以得到: 证明:据式(7) P(Xtj=i) 由于流数据来到的巨量性,在存储空间永远不大于流数据到来个数的情况下,给出的存储方法具有优良的统计性质。这些结论说明,随着时间的不断延续,在连续的等时间间隔区间上进行不放回抽样,并按抽到的样本顺序,用其位置上的样本均值动态存储,每一个存储位置的动态样本都是总体均值的无偏估计和一致估计。样本均值的抽样误差随着抽样批次的增大而减小,当批次充分大时,存储空间的样本均值近似于总体均值,存储样本的抽样误差接近于零,这些不难从定理7和定理8看出。 为了说明本方法操作过程和应用效果,以下采用双气体传感器阵列数据集中乙醇(Ea)变量的2017年1月1日至3月1日的数据分别用单指标抽样动态存储方法和蓄水池抽样方法进行计算。 设每段时间的长度为1天,60天到达的数据个数最小为19 290、最大是60 001,其个数随机且量大。记录的Ea数据代表的是传感器中返回的乙醇浓度,其单位ppm。符合本方法的存储假设。 将60天数据以天为单位分为60段,虽然每天达到的数据量都很大,但具体数量个数不同,设定存储空间为100(即能够存入的数据量为100),应用R软件插入程序编写算法,对第i(i=1,2,…,60)段内的数据按不放回抽取样本100个;再利用均值存储法式(11)对存储空间固定位置的数据进行更新存储,如图1所示。 图1 抽样存储展示图 图1中的60条曲线分别是60段数据抽取100个样本点的记录,通过均值存储计算,最后留在空间内的100个数据点为平均数曲线所展示的部分;该曲线位于60条曲线阴影较重(数据聚集)的地方,可视为抽样存储效果较好;最终仅对平均数曲线数据进行存储。具体数值以10×10的表格展示如表1。 表1 流数据抽样存储最终数据表 从图1中大致判断存储数据的代表性较强,下面通过计算样本方差、总体方差及抽样误差等来展示抽样存储效果。 对蓄水池抽样(Sampling with a Reservoir),应用R软件插入程序编写算法,蓄水池的样本容量仍然设定为nR=100,通过对流数据流入的顺序、利用流入第j(j>100)的数据键值Kj=zj1/wj与事先池中确定的最小键值(Ki=zi1/wi,i=1,2,…,nR)的大小关系判断是否代替“池子”中已有的候选者,得到蓄水池中最终数据如表2所示。 表2 蓄水池抽样存储最终数据表 在假定流数据来到个数和取值双随机的条件下,采用不放回抽样方法,一是证明了样本均值的期望与条件分布有关,特殊情况下样本均值为总体均值的无偏估计;二是给出了总体方差的无偏估计;三是在有限的存储空间内,给出了动态样本存储方法并证明了动态样本均值是总体均值的一致、无偏估计量。四是得出动态样本的抽样误差与反复抽样批次与存储空间容量的乘积的倒数同阶。 通过本方法的设置条件可以看出,这种抽样与存储适用于平稳的流数据,有着较广泛应用范围。对于随着时间变化而不断偏离的流数据,有待于进一步研究。


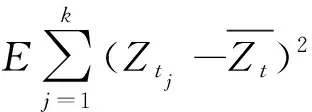

三、流数据样本存储及其误差估计
(一)存储流数据抽样样本的方法


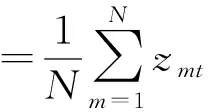


(二)存储样本数据的误差估计








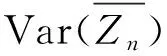




四、应用实例
(一)流数据动态存储方法





(二)蓄水池抽样方法


五、结束语

