基于置信水平的毕达哥拉斯模糊综合评价方法
曾守桢,张崇辉
(1.宁波大学 商学院,浙江 宁波 315211;2.浙江工商大学 统计与数学学院,浙江 杭州 310018)
一、引言
综合评价是管理学和统计学方法体系的一个重要分支,其理论与方法已广泛应用于经济、管理、工程和军事等诸多领域,如经济效益评价、市场化进程测评、信息化测评、竞争力评价、环境质量评价、小康社会及和谐社会评价等等。在现实很多综合评价问题中,评价者不仅需要给出评估对象的“评估值”,同时也要求给出对该评估值的熟悉程度”或“置信度”,或者称为“置信水平”。例如,在博士论文、期刊论文、奖获评审、国家自然科学基金项目评审等问题中,专家在给出“评估值”的同时,还须以类似“熟悉程度”等形式说明自己评判的可靠性。“置信水平”的实质就是评审专家对自己评判的可靠性的主观评价,应该受到重视。然而如何规范地将“置信水平”信息融入专家的最终评判评估结果并以此做出决策却成了难题。针对此类考虑置信水平的评价问题,朱卫东等提出利用历史评估结果的准确性衡量专家提供的评价信息可靠性的方法,进而提出一种基于证据理论的科学基金项目评估决策模型[1]。张洪涛等将同行评议表中的“熟悉程度”信息纳入项目立项评估决策中,并以“熟悉程度”对专家进行赋权,从而构建了多维框架证据推理的科研项目立项评估方法[2]。由于证据理论方法对证据进行合成时,必须考虑证据独立及证据间是否存在强冲等复杂问题,Xia等提出了两种融合评价值和置信水平的简便方法,即置信诱导加权平均(CIWA)算子和置信诱导加权几何(CIWA)算子,并研究了该方法在犹豫模糊信息多指标评价问题中的应用[3]。在CIWA集成方法的基础上,Yu提出了置信有序加权平均(COWA)算子,并研究了该方法的优点和性质[4-5]。由于集成规则简便有效,该 COWA算子目前得到了众多学者的关注,如Yu研究了COWA集成方法在直觉模糊情形中的应用,提出了一系列的置信直觉模糊信息集成方法,如置信直觉模糊有序加权平均(CIFOWA)算子和置信直觉模糊爱因斯坦加权平均(CIFEWA)算子等,并研究了这些算子在博士论文评审中的应用[4]。Ma和Zeng进一步提出了置信直觉模糊信息混合加权集成方法[6]。针对评价信息为语言变量的评价问题,Zhang等研究了COWA算子在语言情形中的应用,提出了几种基于语言信息的置信加权方法,并研究了这些方法在基金和论文评审中的应用[7]。
从以上研究可看出,现有的置信算子能有效地将评价值和置信水平融合到评估结果中,且计算简便,得到了广大研究者的推广和使用。然而现有方法存在两个明显的缺陷:一是不能有效体现置信水平在集成过程的诱导作用,如朱卫东等和张洪涛等只是简单将专家置信度与评价信息集成,未考虑其对专家重要性的诱导作用[1-2];二是该算子不具备有界性,如Xia等构造的CIWA和COWA算子不满足集成算子的有界性,使得最终评估值不具备可比性和科学性[3-5]。基于此,本文拟提出一种融合专家“评价值”和“置信水平”的新集成方法,从而改进现有方法的缺陷,并探讨其优良性质和在毕达哥拉斯模糊情形中的应用,最后将该方法应用于博士论文评审问题中以检验其有效性。
二、置信诱导有序加权算子
在很多实际综合评价问题中,为了提高评价结果的科学性,专家在给出评估值的同时,往往还须以类似“置信水平”(或“熟悉程度”)等形式说明自己评判的可靠性。设ai(i=1,2,…,n)是专家对方案指标的评价值,li(i=1,2,…,n)是与评价值ai(i=1,2,…,n)相对应的置信水平,为了有效融合专家“评价值”和“置信水平”信息,基于有序加权(OWA)算子的思想[8],Yu[4]提出了置信有序加权平均(COWA)算子,其定义如下:
定义1设COWA:Rn×Rn→R,若
COWA(
(1)

由以上定义可知,COWA首先对置信水平与评价值的乘积大小进行排序,然后按照从大到小与权重w=(w1,w2,…,wn)T加权集成,其实质还是一种有序加权平均算子,并没有体现置信水平作为诱导变量的作用。另外,该方法在应用中存在无界性的缺陷,下面通过例1进行说明。
例1 设有3名专家对某个方案进行评估打分,满分100分,最低0分。由于专家学科背景与专业的差异,每个专家对评价方案的熟悉度不一样,因而每个专家给出评价信息的同时也给出了其相应的置信度,10表示非常自信,0表示非常不自信。若三位专家给出的置信水平与评价值分别如下:
则有:
l1a1=540,l2a2=560,l3a3=520
从而
lσ(1)aσ(1)=l2a2=560,lσ(2)aσ(2)=l1a1=540,
lσ(3)aσ(3)=l3a3=520
假设与COWA相关联的权重向量为(0.2,0.4,0.4)T,则:
COWA(〈9,60〉,〈8,65〉,〈7,80〉)=0.2×560+0.4×540+0.4×520=424
在本例中,显然第一位专家的置信水平比第二位专家高(l1=9>l3=7),说明第一位专家应该对评价对象比第二位专家更自信和更有把握,因而其意见应该优先集结加权。然而根据方程(1)定义的COWA的加权规则,第二位专家的意见优先于第一位专家加权,从而导致置信度低的意见优先于置信度高的意见加权,这与事实不相符。在实际问题的评价与决策过程中,一般地,若专家给出的置信水平li越大,表示该专家对所要评价的对象比较熟悉,对给出的评价值比较自信,因此对于这种高置信水平对应的评价值ai,应该优先进行加权集成。然而,例1说明COWA算子并不能充分体现置信水平li这样的诱导作用。另外可看出该方案的最终评价值为424,远远高于其满分100,从而导致该评价值不具有科学性和可比性,其原因如前所述,主要是因为COWA算子不具备有界性。
为克服上述缺陷,下面提出一种新的融合专家评价值和“置信水平”信息的集成方法,定义如下:
定义2设CIOWA:Rn×Rn→R,若
CIOWA(
(2)

现在利用CIOWA算子对例1中的数据进行集成,即三位专家给出的置信水平与评价值分别如下:
则有:


同理可得:
r2=0.410,r3=0.359
根据CIOWA的运算规则,
CIOWA(〈9,60〉,〈8,65〉,〈7,80〉)=0.231×60+0.410×65+0.359×80=69.23
可以看出,CIOWA算子在集成过程中完全根据置信度的大小进行诱导加权,即置信水平高的评价值优先集成,从而充分考虑和尊重了更自信和更有把握的评价意见,而且最终评价值为69.23,介于最高评价值和最低评价值间,克服了COWA算子集成结果不能满足有界性的缺陷。
特别地,下面证明经典的诱导有序加权平均(IOWA)算子[9]是CIOWA算子的特例。
命题1IOWA算子是CIOWA的特例。
证明:设l1=l2=…=ln=l,
则

从而
CIOWA(
=IOWA(
证毕。
CIOWA算子具有一般加权算子良好性质,如有界性、单调性和幂等性等。下面仅证明CIOWA的有界性,其他性质可类似证明。
命题2(有界性) 设


CIOWA(


=CIOWA(
从而有
x≤CIOWA(
证毕。
在实际评价与决策问题中,往往需要考虑评价指标的权重,然而CIOWA算子只考虑了加权位置的重要性,具有一定的局限性,为此进一步提出置信诱导混合加权(CIHW)算子,定义如下:
定义3设CIHW:Rn×Rn→R,若
CIHW(
(3)

下面证明CIOWA算子是CIFHW的特例。
命题3CIOWA算子是置信诱导混合集成算子CIHW的特例。

CIHW(
=CIOWA(
证毕。
显然,CIHW兼具CIOWA算子的性质和优点,既考虑了待集成评价值的重要性又考虑了其所在位置的重要性。然而CIHW只适用于评价值为实数的情形,下面研究其在毕达哥拉斯模糊集情形中的应用。
三、基于毕达哥拉斯模糊信息的CIHW集成方法
Atanassov改进了仅仅考虑隶属度的传统模糊集的缺陷,提出了同时考虑隶属度、非隶属度和犹豫度这三个方面信息的直觉模糊集[10]。直觉模糊集在处理模糊性和不确定性等方面更具灵活性和实用性,引起了众多研究者越来越多的重视和关注,相应的成果也较丰富[11]10-54[12]8-15[13]12-18[14]10-20。然而在直觉模糊评价和决策的过程中,Yager教授发现专家给出的方案满足指标(属性)的隶属度和非隶属度之和往往出现大于1的情况,为此,Yager定义了一种新的模糊集—毕达哥拉斯模糊集[16],其特征是允许隶属度和非隶属度之和超过1,而其平方和不超过1,从而使得专家在评价过程中不必重新修改直觉模糊评价值也可以进行决策。近期众多学者从信息集成、距离测度和模式识别等不同角度对毕达哥拉斯模糊集进行了深入的拓展研究[17-21]。本节将研究基于毕达哥拉斯模糊的CIHW算子集成方法。首先简单回顾毕达哥拉斯模糊集的定义及其运算规则。
定义4[16]设X为论域,则称
A=〈x,μA(x),vA(x)〉x∈X
(4)
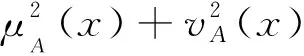

(1)若s(α1) (2)若s(α1)=s(α2),则: 若h(α1) 若h(α1)>h(α2),则α1≻α2; 更多关于毕达哥拉斯模糊数的运算规则和集成方法可参见Yager Ronld R和Zhang Xiao lu等的研究文献[16-17]。 信息集成是毕达哥拉斯模糊集理论研究中的一个重要领域,Yager提出了毕达哥拉斯模糊加权平均算子(PFWA)[16],在此基础上,Zhang和Xu提出了毕达哥拉斯模糊有序加权算子[17]。刘卫锋等提出了一系列的毕达哥拉斯模糊拟加权平均算子和拟加权几何算子,刘卫锋等定义毕达哥拉斯模糊数的交叉影响加法、数乘、乘法及幂运算,在此基础上研究了基于毕达哥拉斯模糊信息的交叉影响加权集成方法,Zeng等提出了毕达哥拉斯模糊混合有序加权距离算子,并研究了其在多属性决策问题中的应用[23-25]。 然而以上毕达哥拉斯模糊信息集成算子都不能对“置信水平”信息进行有效集成,为此下面将研究CIHW算子在毕达哥拉斯模糊集情形中的应用,提出置信诱导毕达哥拉斯模糊混合加权(CIPFHW)集成算子,定义如下: 定义6设αj=(μj,vj)(j=1,2,…,n)为一组毕达哥拉斯模糊数,且设CIPFHW:Rn×Ωn→Ω,若 CIPFHW( (5) CIPFHW( (6) 例2 设α1=(0.5,0.8)、α2=(0.7,0.7)、α3=(0.6,0.3)为3个专家给出的毕达哥拉斯模糊评价信息,专家的权重向量是ω=(0.4,0.5,0.1)T,专家对自己给出意见的置信水平向量是l=(0.7,0.9,0.5)T。下面利用CIPFHW算子计算3名专家对该方案的评价结果。 首先对置信水平进行排序,可得: lσ(1)=0.9,lσ(2)=0.7,lσ(3)=0.5 这里平衡系数n=3,根据毕达哥拉斯模糊运算法则求得加权评价值: =(0.797,0.586) =(0.540,0.765) =(0.354,0.697) 假设w=(0.2,0.5,0.3)T为CIPFHW算子相关联的加权向量,根据置信水平计算权重rj: =0.265 =0.515 =0.220 则由式(5)或式(6),可得: CIPFHW( 下面研究CIPFHW算子的几种特殊形式: (1)当ω=(1/n,1/n,…,1/n)T,则CIPFHW退化成置信诱导毕达哥拉斯模糊有序加权平均(CIPFOWA)算子: CIPFOWA( (7) 其中,w=(w1,w2,…,wn)T为CIPFOWA相应的权向量,(σ(1),σ(2),…,σ(n))是(1,2,…,n)的任一置换,使得对任意的j,有lσ(j-1)≥lσ(j),βj是与置信水平lσ(j)相对应的PFN评价值。 (2)当w=(1/n,1/n,…,1/n)T,CIPFHW算子退化为置信诱导毕达哥拉斯模糊加权平均(CIPFWA)算子: (8) (3)当l1=l2=…=ln=l,评价值的置信水平都一致,则CIPFHW算子退化为毕达哥拉斯模糊混合加权平均(PFHW)算子: (9) 步骤1专家对评价方案Ai(i=1,2,…,m)的各项评价指标Gj(j=1,2,…,n)进行评估,给出的评价信息为αij=(μij,vij)(i=1,2,…,m;j=1,2,…,n),从而可得到方案的毕达哥拉斯模糊评价矩阵R=(αij)m×n。 步骤2专家根据自己对决策方案的熟悉程度,给出与评估值αij相应的置信水平lij(i=1,2,…,m;j=1,2,…,n)。 步骤3利用CIPFHW算子对评价矩阵R=(αij)m×n中的第i行的所有元素αij(i=1,2,…,m)进行集结,得到方案Ai(i=1,2,…,m)的综合评价值αi(i=1,2,…,m) αi=CIPFHW( i=1,2,…,m (10) 步骤4计算综合评价值的αi(i=1,2,…,m)的得分函数s(αi)(如有必要再精确函数h(αi))(i=1,2,…,m),并根据PFN的比较规则对各方案进行排序,从而得到最佳方案。 下面将以论文评审的例子说明基于CIPFHW算子的多指标综合评价方法的实用性。 例 3[4]设某高校进行优秀论文评审,要求评审专家主要从以下几方面进行评估:G1选题与文献综述;G2创新性;G3理论深度与专业知识;G4科学研究能力;G5写作能力。设专家对5份审评论文Ai(i=1,2,3,4,5)进行打分,评价结果如下: 表1 专家评价矩阵 为了更加全面地对论文进行评审,学校要求评审专家对论文的5个评价指标的熟悉程度进行打分(分值范围从0到1,1是非常熟悉,0完全不熟悉),设专家对指标的熟悉程度给出的分值是lj=(0.8,0.7,0.9,0.8,0.6)(即置信水平)。设5个指标的权重向量是ω=(0.1,0.3,0.1,0.3,0.2)T,与CIPFHW相关联的权重向量是w=(0.11,0.24,0.30,0.24,0.11)T,则根据CIPFHW集成方法可得5份论文的综合评价值如下: α1=(0.659,0.300),α2=(0.767,0.317), α3=(0.720,0.320),α4=(0.671,0.384), α5=(0.683,0.322) 计算αi(i=1,2,…,5)的得分函数s(αi)(i=1,2,…,5): s(α1)=0.344,s(α2)=0.488,s(α3)=0.416, s(α4)=0.302,s(α5)=0.363 由于 s(α2)>s(α3)>s(α5)>s(α1)>s(α4) 因此论文排序方案A2≻A3≻A5≻A1≻A4,即A2为最优论文。 如果不考虑专家的置信水平,即假设专家对论文的每个评价指标领域都一样熟悉,确信自己能给出十分确信的判断,则直接用毕达哥拉斯模糊混合加权(PFHW)算子集成专家评价信息,可得到5篇论文的综合得分分别为: s(α1)=0.369,s(α2)=0.513,s(α3)=0.425, s(α4)=0.314,s(α5)=0.359 可以看出最优的论文也是A2,但是后面3篇论文的排序发生了明显的变化,说明置信水平信息将影响方案评估的最终结果。由于评估者往往来自不同的机构部门,其专业背景和工作领域可能不同,必然导致对某些领域熟悉,而其余的领域不太熟悉或者陌生。因此,在对各方案评价过程中,为提高评价结果的科学有效性,评价者在给出评价值的同时,可给出类似“熟悉程度”等形式说明自己评判的可靠性,也即评价值的置信度,从而保证评价者能够真实主动给出自己的评判。文中例题显示,本文提出的融合专家“评价值”和“熟悉程度”的集成模型,改进了现有方法的缺陷,能有效集结专家对该领域的熟悉程度和判断水平,从而得到的评估结果更加合理和可信。 本文融合专家“评价值”和“熟悉程度”的集成模型,研究了其在毕达哥拉斯模糊情形下的综合评价方法。在很多实际工作中,如国家自然科学基金通讯评议及博士论文评审等,专家不仅要给出关于评价对象的“评估值”,还须以类似“熟悉程度”等形式说明自己评判的可靠性。分析现有的集成算子的不足之处,本文提出了一种改进的集成方法,并对其有效性理论进行充分的论证,探讨了新集成方法与现有集成算子之间的关系;其次研究了该置信集成方法在毕达哥拉斯模糊情形的应用,提出了相应的评价方法及其在博士论文评审中的应用。该方法不但计算简便快捷,充分利用已有的评价信息,而且能充分考虑专家的置信水平,增强了评价结果的正确性和合理性。因而,该方法具有较高的实用价值,可应用于投资决策、人事管理、项目评估、经济效益综合评价等诸多领域。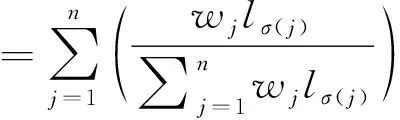






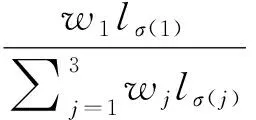


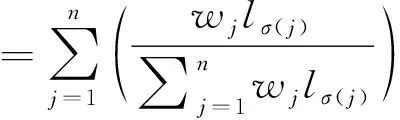


四、基于CIPFHW算子的毕达哥拉斯模糊综合评价方法


五、结论

