基于混合果蝇优化算法的现场服务调度问题
吴 斌,王 超,董 敏
(南京工业大学 经济与管理学院,南京 211816)
0 引言
现场服务通常指在顾客指定的地理位置,满足顾客需求而进行的一系列活动。现场服务广泛存在于各个行业,如电力、通信系统的维护保障,家电、家具行业的售后安装维修、医疗健康领域的家庭看护,制造企业的维护、维修、运行设备(Maintenance, Repair & Operations, MRO)服务等。据统计,仅上海市2010年的家电行业服务产值已达20亿元。2014全球航空企业的MRO的服务产值超过50亿美元。随着大数据、移动互联网等信息技术的发展,线上到线下(Online To Offline, O2O)等商业模式的兴起,顾客的个性化需求和定制化服务需求的日益增多,现场服务的作用愈发重要。现场服务的效率和质量与服务人员的合理配置及线路规划密切相关[1]。不合理的任务及线路安排,容易出现员工在途时间长、顾客等待时间长、员工技能与任务不匹配等问题,从而影响服务质量和服务效率,进而影响顾客的满意度,最终导致企业利润的下降,因此,现场服务调度问题至关重要。
现场服务调度是一个新兴的研究课题,国内外相关的文献较少。Lesaint等[2]针对英国电讯公司通信网络维护中员工的任务与线路安排问题,首次提出了现场服务调度的概念;但他们并没有给出问题的模型和求解算法。Xu等[3]考虑服务任务的类型、优先级以及顾客时间窗等约束条件,以服务任务数量最大、员工工作时间最短为优化目标,建立了现场服务调度的模型,提出自适应贪婪随机搜索算法进行优化求解。在此基础上,Akjiratikarl等[4]将员工的旅行距离最短作为优化目标进行研究,提出粒子群算法进行优化求解。Goel等[5]以电网停工时间和人员旅行时间最短为优化目标,研究了电网维修人员的现场服务调度问题,提出了爬山法、大邻域搜索等多种优化算法。江俊杰等[6]除了将员工的旅行时间和等待时间作为优化目标外,还将客户满意度作为优化目标,提出了基于分段染色体编码的遗传算法(Genetic Algorithm, GA)。Xu等[7]强调了员工的综合技能和团队合作等约束条件,提出了改进的非支配排序遗传算法(Non-dominated Sorting Genetic Algorithm, NSGA-Ⅱ)。Borenstein等[8]采用分区的方法,研究了英格兰电信的动态现场服务调度问题,提出基于规则的算法进行优化求解。Kovacs等[9]研究了需要团队合作的现场服务调度问题,同时考虑对不能完成的任务采用外包,将旅行线路和外包费用作为优化目标,提出自适应大邻域搜索算法进行优化求解。Damm等[10]基于文献[3]的模型,以最大化完成任务的优先级为主要优化目标,提出偏置随机关键遗传算法(Biased Random Key Genetic Algorithm)进行优化求解。Pillac等[11]分析了现场服务调度问题(Field Service Scheduling Problem, FSSP)与带时间窗车辆路径问题(Vehicle Routing Problem with Time Windows, VRPTW)的区别,提出并行自适应大邻域搜索算法优化求解该问题。此外,Cortes等[12]采用分支定价算法(branch-and-price)求解了一个实际公司维修数码设备的现场服务调度问题。Tang等[13]、曹永荣等[14]以M/G/m排队模型为基础,通过仿真的方法研究了现场服务调度问题。
目前关于现场服务调度问题的求解算法多基于经典算法,如遗传算法等,缺少对新型算法的挖掘和优选。果蝇优化算法(Fruit fly Optimization Algorithm, FOA)是一种新型的群智能优化算法,具有算法简单、参数少、收敛速度快等优点,已经在函数优化[15]、神经网络[16]、背包问题[17]、车间调度问题[18]等领域成功应用,但还未在现场服务调度问题中应用。本文基于果蝇优化算法,提出求解现场服务调度问题的算法框架,设计了编码方法和优化算子,为现场服务调度问题的求解提供了新思路,既丰富了现场服务调度的求解算法,又扩展了果蝇优化算法的应用领域。
1 现场服务调度问题的模型
现场服务调度问题可以描述如下:将n个分散在不同地点的客户服务任务分配给m个工人。每个服务任务有时间窗和工人的技能要求。工人从不同的地点出发,巡回服务,结束后返回各自地点;每个工人掌握的技能不同,需要和服务任务匹配。该问题的优化目标是工人的旅行时间、任务的完成时间和工人的等待时间最短。建立的混合整数规划模型如下。
对于一个网络G={V,E},其中集合V={D,C},包含工人集合D={0,1,…,m-1}和任务集合C={0,1,…,n-1}。E={(i,j)},i,j∈V表示连接结合,cij表示i到j的旅行时间,且cij=cji。di表示任务i的标准服务时间,λki∈(0,M]表示工人k服务任务i的熟练程度,λki越小表示熟练程度越高,完成时间越短;λki>M则表示无法完成该任务。[Ei,Li]表示任务i的时间窗;ti表示任务i开始服务的时间;wi(ti)表示工人在任务i的等待时间。xijk=1,i,j∈V,k∈D表示工人k从节点i到j;否则xijk=0。yik=1,i∈C,k∈D表示任务i被工人k服务;否则yik=0。
(1)
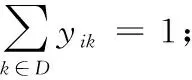
(2)
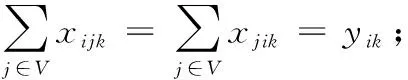
(3)
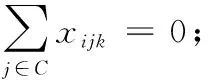
(4)
tj=max{Ej,ti+λkidi+cij}
(5)
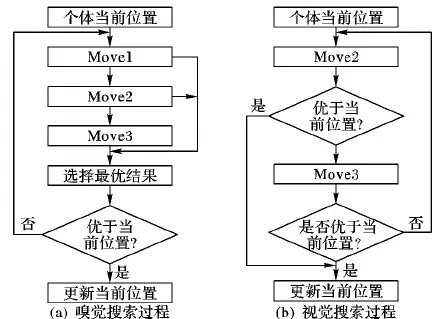
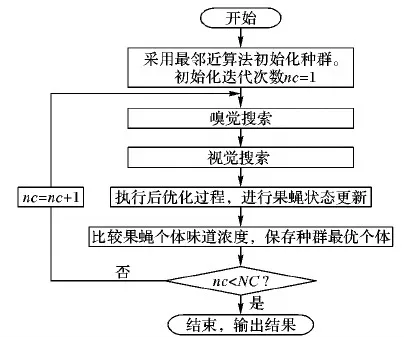
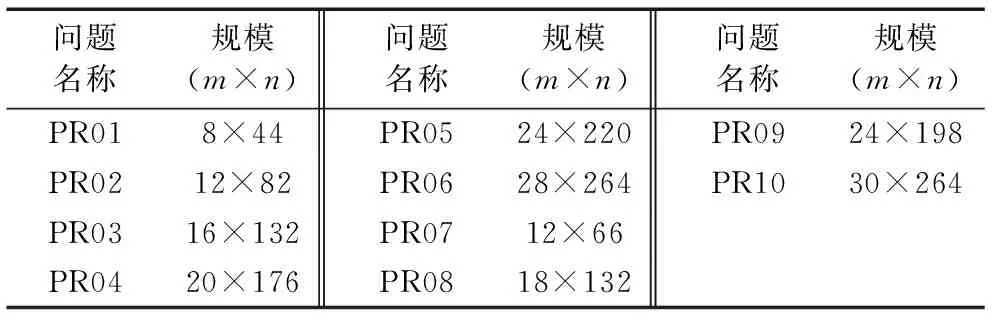
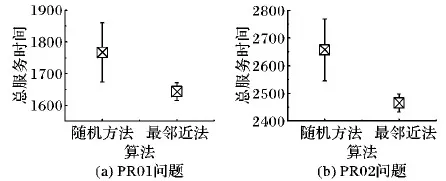
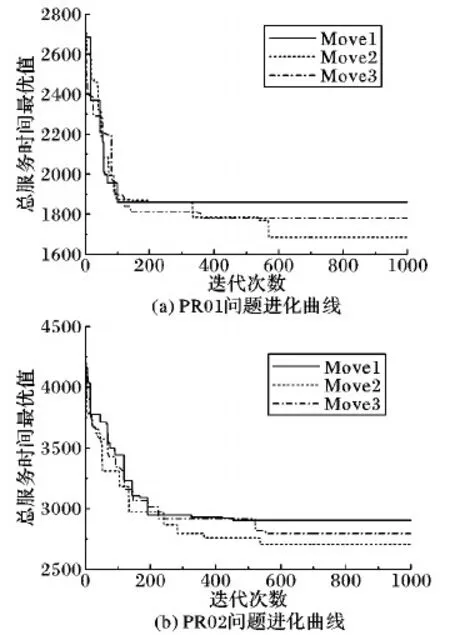
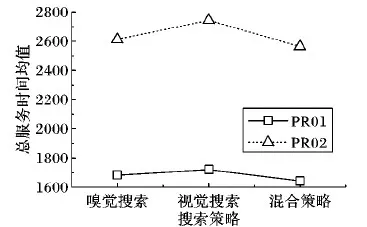
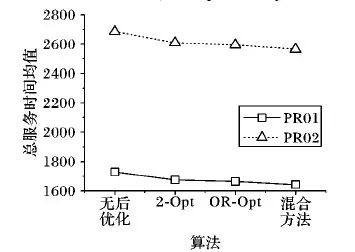
tj (6) wj(tj)=max{0,Ej-tj} (7) 式(1)表示目标函数,由三部分组成:第1部分是旅行时间,第2部分是任务的完成时间,第3部分是工人的等待时间,通过加权使三者之和最小。约束式(2)保证每个任务点仅被1个工人服务。约束式(3)保证每个任务仅被服务1次,且工人进入节点并从该节点离开。约束式(4)表示工人需从自己的出发地出发。约束式(5)和(6)表示时间窗的约束,约束式(7)表示等待时间的计算。 果蝇优化算法(FOA)是一种基于果蝇觅食行为的群智能优化算法[19]。果蝇有很好的嗅觉和视觉器官,能够依靠嗅觉感觉到40 km外的食物源,然后在邻近食物源时,依靠敏锐的视觉发现食物的具体位置。果蝇算法模拟该过程,基于嗅觉和视觉行为进行迭代搜索,通过对果蝇种群位置中心的优化,最终获得问题的优化解。果蝇算法的基本流程如下。 步骤1 初始化种群中个体的位置。 步骤2 嗅觉搜索。由个体的当前位置随机选择方向和位置进行搜索。 步骤3 个体评价。对个体搜索到的新位置,计算其味道浓度。 步骤4 视觉搜索。选择味道浓度最大的位置,个体根据视觉向该位置搜索。 步骤5 判断算法是否结束:是,则输出最优解;否,则转步骤2进行迭代。 基本的果蝇算法主要用于函数优化,将其应用于现场服务调度问题,需要在编码方法、初始化方法、嗅觉搜索和视觉搜索等方面进行改进。 现场服务调度问题是组合优化问题,果蝇优化算法在求解这类问题时,如何进行编码是关键。本文提出一种基于矩阵的编码方式表示现场服务调度的解,这种编码方法可以将任务分配与工人旅行线路同时表达出来,方便果蝇优化算子的设计。其编码方式如下: (8) 步骤1j=0。 步骤2 选择第行所有的非0元素组成的向量(ajl,ajm,…,aji),则其对应的任务为(l,m,…,i)。 步骤3 将(ajl,ajm,…,aji)中的元素从小到大排序,得到(l,m,…,i)的任务排序,依次将客户分配给工人,同时判断是否满足时间窗限制;如果不满足,则将任务分配给距离最近或开始时间最早的工人。 步骤4 如果j=m-1,则结束程序;否则j=j+1转步骤2。 例1 以3个工人、6个任务的现场服务系统为例,其编码形式如下所示: 根据解码算法,1号员工分配的任务是(2,4),2号员工分配的任务是(1,5)。3号工人分配的任务是(3,6)。再根据客户对应元素按照从小到大排序,同时考虑时间窗限制,得到员工的旅行线路是:1号的巡回线路是2—4;2号的巡回线路是5—1;3号的巡回线路是3—6。 随机初始化的方法虽然简单,但会产生一些非法解,影响求解质量。采用启发式初始化的方法,可以在初始阶段产生有效解,提高优化的质量。本文基于最邻近启发式算法进行种群的初始化。该算法是求解旅行商问题(Traveling Salesman Problem, TSP)、车辆路径问题(Vehicle Routing Problem, VRP)等的经典算法,其核心思想是在满足一定的约束条件下,在未访问的任务列表中逐步寻找与当前线路中距离最近的任务,然后将其插入线路中。本文由于实际窗的存在,在已经存在的线路中插入客户任务,需要考虑两方面的因素:第一,能力约束,即工人是否能完成该任务;第二,时间是否可行,即插入某一任务后,插入的任务和插入位置以后的任务的时间窗是否满足要求。对于第二种因素,如果插入一个客户,是否要依次检查其后的所有客户是否可行?对此问题,依据作者针对带取送货车辆路径问题(Vehicle Routing Problem with Pickups and Deliveries, VRPPD)提出的可行性插入定理[20],可以得到如下结论。 定理1 对于第f个工人已建立的可行线路i1,i2,…,ip,若在其第k个位置之后插入(ik和ik+1)之间插入一个任务h时,插入可行的充分必要条件是: th (9) λfh≤M (10) 其中:th表示到达任务h的时间;Lh表示任务h最晚允许达到的时间;Δt表示插入h后,车辆到达任务ik+1的时间比原来的推迟量;M表示预设的一个熟练程度值,在本文M=2,即当工人完成某项工作的时间大于标准时间的2倍时,认为工人不能胜任该任务,则该客户不能分配给此工人。 在本文,邻近任务的选择需要考虑工人的等待时间、任务间的行驶时间等因素。设i表示当前线路中的最后一个任务,j表示未访问的任务,cij表示i与j之间的行驶时间,ti表示在任务i处开始服务的时间,wj(tj)表示工人在任务j的等候时间。tj和wj(tj)由式(5)和(7)计算得到。Nij表示任务i与j之间的广义费用,则选择最邻近任务的广义费用可定义如下: Nij=α1×cij+α2×wj(tj) (11) 其中α1,α2为系数,且满足α1+α2=1。通过计算未访问任务的值,选出最小值对应的任务插入线路中。最邻近插入算法的过程如下。 U表示任务集合,Rk表示第k条线路的集合,CLk表示第k条线路的旅行时间,Vj表示工人j的客户集合。 步骤1 设置U=C,k=0,Rk=∅,CLk=0,j=0。 步骤2 判断任务集合U是否为空,如果是则转步骤5。如果不是,则从U中选择开始服务时间最早的任务i,如果其时间窗Li 并把任务i从集合中删除。 步骤3 根据插入可行性定理1,从集合U中选择未服务的可行任务。根据式(11)计算这些任务的插入值Nij,选择最小的插入线路,更新CLk和集合U。重复上述过程,直至没有可行客户为止。 步骤4 计算Rk中任务的重心,选择距离该重心最近的员工j,将Rk的元素插入Vj中。k=k+1,CLk=0,转步骤2。 步骤5 将构造的初始解映射为果蝇优化算法的编码。 由于采用矩阵的编码方式,现有果蝇算法的状态更新方程不再适用。本文根据现场服务问题的特征,基于群智能理论和社会心理学原理,提出以下3种果蝇搜索策略。首先本文定义以两种矩阵操作:posSwap(m,k)和valueSwap(m,k)。 1)posSwap(m,k)表示将矩阵A的第m行(或列)与第k行(或列)的元素互换,同时对于所有非零元素进行如下计算: (12) 2)valueSwap(m,k)表示将矩阵A中第k列的第m行元素进行重新赋值。执行该操作时,首先根据式(13)计算amk,然后将该列除此元素之外的所有元素置0,以保证解的合法性,即每个任务只能分配给一个工人: (13) 3种果蝇搜索策略分别定义如下: Move1m∈D,k∈D,posSwap(m,k)。表示两个工人之间互换所有任务,同时任务的服务顺序可能发生改变。 Move2m∈C,k∈C,posSwap(m,k)。表示将任务和互换,该操作可以使任务在工人之间交换,同时也可以改变任务在工人中的访问顺序。 Move3m∈C,k∈D,valueSwap(m,k)。表示将任务k分配给工人m,该操作可以改变任务的分配,同时改变任务在工人中的访问顺序。 在果蝇算法中:由于果蝇的嗅觉灵敏,可以在大范围内搜索,因此嗅觉搜索主要负责解空间的开发探索(exploitation),它的搜索范围比较大;当距离事物源较近时,则转为视觉搜索,视觉搜索主要负责解空间的精细搜索(exploration)。根据上述原理,本文所提算法在嗅觉搜索中,依次执行Move1、Move2和Move3搜索,根据最好接受(Best Acceptance)策略,选择搜索到的最好位置信息更新当前果蝇的状态;在视觉搜索过程中,仅执行Move2和Move3搜索,根据更好接受策略(Better Acceptance),当搜索到比当前果蝇状态更好的位置时,即进行更新。嗅觉搜索和视觉搜索的过程如图1所示。 图1 FOA的搜索过程 在执行完果蝇优化算法的搜索过程后,为了提高优化质量,使用局部搜索算法对每个解进行改进,此处主要采用两种改进算法:2-Opt和OR-Opt。后优化过程采用更好接受策略,当搜索到比当前解更好的解时,对果蝇的状态进行更新。混合果蝇优化算法的流程如图2所示。 目前现场服务调度问题没有测试实例库,本文基于带时间窗的多仓库车辆路径问题(Multi-Depot Vehicle Routing Problem with Times Windows, MDVRPTW)的实例库[21],构建现场服务调度问题的实验数据。原有数据的坐标、时间窗、操作时间等信息不变,忽略其中的客户需求量等信息。工人数量设定为与原实例中车辆数量相等,在将原有的仓库位置设定为现场服务调度中工人位置的同时,还需要将一些客户位置设定为工人位置。此外,对于每个实例还需要生成一个工人操作任务熟练度的矩阵,此矩阵随机生成。其中:λki的取值范围是[0.5,3],λki越小表示完成任务所需要的时间越短,操作越熟练,λki>2表示工人无法完成此任务。 图2 混合果蝇优化算法求解现场服务调度问题的流程 对于实例中的PR01问题,原问题表示有4个仓库、48个客户、每个仓库有2辆车的问题,在转换成现场服务调度问题时,则是有8个工人、44个客户的问题,其中4个工人的地址是原仓库地址,其余4个工人地址是从原48个客户中随机选择4个设定的。根据此方法,选择10组实例进行测试,问题规模如表1所示。 表1 仿真实例描述 混合果蝇优化算法用C++语言实现,运行在酷睿i5 2.5 GHz,4 GB内存的计算机平台上。果蝇算法的种群规模P=100,迭代次数NC=1 000,目标函数的系数α=0.4,β=0.3,γ=0.3。针对每个实例,算法随机运行20次,对其结果进行统计分析。首先对本文提出的初始化方法进行分析比较,最邻近法的初始化参数α1=0.6,α2=0.4,将最邻近算法和随机初始化进行对比。针对PR01和PR02进行测试,优化结果的均值和方差如图3所示。 图3 果蝇优化算法初始化方法的比较 从图3中可以看出,最邻近法比随机方法的均值有明显降低(对于PR01问题,与随机方法相比,最邻近法均值了减小7%;对于PR02,减小6.9%),并且算法的偏差更小,表明最近邻算法能使果蝇算法更加稳定。 下面对3种局部搜索算子的搜索能力进行比较。依然以PR01和PR02为例,分别单独执行Move1、Move2和Move3三种搜索策略,算法的进化曲线如图4所示。从图4中可以看出,在算法初期(200代以内),3种搜索策略的效率相差不大,都能很快地搜索到比较好的结果;但在迭代后期,Move1算法比较早地进入停滞期,无法跳出局部极值点。这是因为Move1主要将客户在工人之间交换,搜索得比较粗糙。Move2算子在3种搜索策略中优化能力最强,这主要因为Move2操作在进行任务交换的同时,不仅改变了任务在工人间的分配,同时还改变了任务的访问顺序,是一个集成了线路内和线路间的2-Opt算子。Move3类似于一个插入算子,搜索能力比Move1强,但比Move2弱。 图4 3种搜索算子的比较 对于嗅觉搜索和视觉搜索的搜索能力,本文也通过PR01和PR02两个问题进行了验证,结果如图5所示。 图5 搜索策略的比较 从图5可以看出,仅执行视觉搜索的结果最差,嗅觉和视觉都执行的混合策略优化结果最好。因为视觉搜索主要是由邻域信息引导的局部搜索,采用更优接受(better acceptance)策略。而嗅觉搜索是全局信息引导的搜索,并且3种搜索算子都执行,采用最优接受策略,因此,嗅觉搜索的优化能力更强,当把两种搜索策略混合,视觉的局部搜索能改进嗅觉搜索的优化结果。 图6显示了后优化过程对算法的影响。与没有使用后优化的算法相比,使用后优化过程(两种算子都用)可以将优化的均值提高5%左右(PR01提高4.91%,PR02提高4.45%)。单独使用一种后优化算法子,OR-Opt比2-Opt稍有优势。 图6 后优化过程的比较 最后,将本文提出的混合果蝇优化算法与Xu等[3]提出的贪婪随机自适应搜索过程(Greedy Randomized Adaptive Search Procedure, GRASP)算法和江俊杰等[6]提出的遗传算法进行了比较,结果如表2所示。从表2中数据可以看出,对于10个问题,混合优化果蝇算法在均值和最优值方面都优于GRASP算法和遗传算法,GRASP算法又比遗传算法的优化结果好。 表2 3种算法的均值与最优值比较 随着互联网经济的发展,客户的个性化服务需求日益凸显。现场服务进入飞速发展阶段,为了提高服务质量和效率,现场服务调度至关重要。本文建立了现场服务调度问题的数学模型,分析了问题解的性质(插入可行性)。鉴于问题的复杂性,提出了混合果蝇优化算法进行求解。设计了基于矩阵的实数编码方案,基于群智能理论和社会心理学原理,定义了两类矩阵操作算子,设计了3种搜索策略,进而重构了果蝇优化算法的嗅觉搜索和视觉搜索过程。为了提高算法的性能,构建了基于最邻近插入启发式算法的初始化方法,并引入后优化过程。通过实验仿真,分析比较了各算子的优化效果,并与其他算法进行了比较。结果表明,本文所提算法是求解现场服务调度问题的有效方法。2 基本果蝇优化算法
3 混合果蝇优化算法求解现场服务调度问题
3.1 编码方法


3.2 种群初始化
3.3 果蝇搜索策略
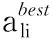
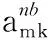
3.4 后优化过程
4 实验仿真

5 结语

