基于数据过采样和集成学习的软件缺陷数目预测方法
简艺恒,余 啸
(1.北京理工大学 信息与电子学院,北京 102488; 2.武汉大学 计算机学院,武汉 430072)
0 引言
软件在如今社会发挥着举足轻重的作用,复杂系统的可靠性高度依赖于软件的可靠性。软件缺陷是导致系统失效和崩溃的潜在根源[1],如果能对软件缺陷进行预测,就能在造成危害前对软件缺陷进行排查和修复,从而减少软件崩溃所带来的经济损失。
伴随着第一个软件的诞生并延续至今,软件缺陷预测技术已得到了长足的发展[2]。已有很多研究提出了很多软件缺陷预测方法。如文献[3]探索了传统的机器学习模型和半监督学习在软件缺陷预测中的应用,并在PROMISE数据集上进行测试,达到了工程的需求。文献[4]比较了包括决策树、贝叶斯、向量机、人工神经网络等传统机器学习模型在多机构数据集上的预测表现。
但是这些模型仅仅是基于分类问题,将软件模块分为由缺陷和无缺陷两类,不能预测出软件缺陷数目。如果能够预测软件缺陷数目,就能将有限的软件资源优先分配给软件缺陷数目多的模块,从而提升测试的效率。举例而言,假如预测出一个软件中有40个模块具有缺陷,而测试人员因测试资源有限,只能对其中10个软件模块进行测试。如果使用基于分类的预测方法预测出有15个软件模块有缺陷,测试人员只能随机抽取其中的10个模块进行测试,但如果能够预测出软件缺陷模块的具体数目,那么测试人员可以优先测试缺陷数目多的10个模块,大大提升了测试效率。
目前针对软件缺陷数目的预测亦有一些研究。如文献[5]构建了一个灵活的贝叶斯网络,利用贝叶斯网络进行软件缺陷数目的预测,取得了稳定的输出效果;文献[6]提出了一个基于缺陷状态转移模型的软件缺陷数目预测方法,并且在软件开发实践中得到了验证,但是这些研究却忽略了软件缺陷数目分布不平衡的问题,即软件中缺陷数目为0的软件模块的数量一般远多于缺陷数目大于0的软件模块数量。如果对软件模块训练数据不作任何处理,会导致训练出的软件缺陷数目预测模型对多数类样本(缺陷数目为0的软件模块)具有偏向性,从而对少数类样本(缺陷数目大于0的软件模块)的预测方面存在失真。而对缺陷模块具有的缺陷数目的准确预测正是软件缺陷预测技术的重点。故在进行软件缺陷数目预测的时候,有必要解决软件缺陷数据集的不平衡性问题。
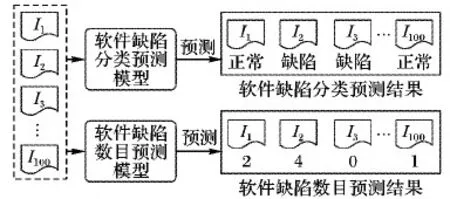
图1 软件缺陷分类预测与数目预测区别
针对不平衡数据集的处理通常包含代价敏感方法和采样方法。文献[5]指出虽然代价敏感方法能够有效地提高稀有类的识别率,但是仍存在若干局限,例如错误代价难以被精确估计,从而影响代价敏感的效果。采样方法分为欠采样方法和过采样方法,其中文献[6]表明欠采样通过删除部分多数类样本使数据分布重新平衡,但会造成信息的丢失。过采样方法通过增加少数类样本的数量使数据分布重新平衡,保留了所有的信息,相比欠采样方法有更好的效果。文献[7] 提出了一种基于SMOTE(Synthetic Minority Over-sampling TEchnique)过采样的SMOTER(SMOTE for Regression)方法用于软件缺陷数目预测,具有普适性强和易于其他模型组合的优点,实验结果表明该方法具有良好的性能表现。
但是不平衡数据再平衡后,使用单一的回归模型,容易出现过拟合降低了模型的稳定性。集成学习通过构建并合并多个个体学习器来完成学习任务,常可获得比单一学习器更显著优越的泛化性能。目前已有的研究普遍采用了集成学习的方法,在实验中取得了较高的准确性和稳定性[8-10]。
目前的研究针对软件缺陷数目预测模型的评价指标一般为预测缺陷数量与实际缺陷数量的绝对误差和相对误差,如文献[11-12],但是这些评价指标同样没有考虑到软件缺陷不平衡的问题,由于软件缺陷数目分布不平衡问题,这类评价指标容易导致评价过于乐观。本文采用专门用于软件缺陷数目预测领域的FPA(Fault-Percentile-Average)指标[13],能够有效地表现出预测模型的准确性。
本文在现有研究的基础上,结合过采样方法和集成学习的方法,提出了一种基于数据过采样和集成学习的软件缺陷数目预测方法——SMOTENDEL(SMOTE for predicting the Number of Defect using Ensemble Learning)。该方法首先通过数据不平衡率确定过采样比例,执行n次过采样方法,得到n个不同的平衡的软件缺陷数据集;然后基于这n个平衡的软件缺陷数据集训练出n个个体学习器;最后,对这n个个体学习器通过集成得到一个组合学习器,并利用这个组合学习器来预测待预测的软件模块的缺陷数目。
1 相关工作
目前对软件缺陷的预测已有不少研究,其中可分为两大类:一种是预测软件模块是否有缺陷,一种是预测软件模块具体的缺陷数目。
1.1 预测软件模块是否有缺陷
文献[14]针对目前软件缺陷预测方法大多是针对特定的数据集建立的模型的现状,研究了跨项目软件缺陷预测的方法,发现将针对特定数据集的模型与跨项目模型的预测结果相比,只存在微小差异,在此基础上建立了一种跨项目软件缺陷预测模型,取得了更高的性能表现。文献[15]提出了一种跨项目软件模块缺陷预测方法,建立了基于元分类逻辑回归预测模型,使用成本效益和F-measure作为评价标准,实验结果表明该模型相较于常规的逻辑回归预测模型在F-measure上和平均F-measure上提升了36.88%;文献[16]比较了基于信息增益特征选择算法(GIS)和基于近邻的遗传算法(NN-filter)的预测性能,实验结果表明GIS方法在多个指标上取得了最优的表现;文献[17]提出了一种多目标优化的JIT-SDP(Just-In-Time Software Defect Prediction)方法,使用逻辑回归方法建立模型,实验结果表明该模型的预测能力强于目前最先进的监督学习和非监督学习模型,且在跨项目、跨时间预测上同样有良好的表现。上述方法没有进行软件缺陷数目的预测,虽然可以预测出软件缺陷模块,但是在测试资源有限的情况下无法合理分配资源,优先测试具有更多缺陷的软件模块,会造成测试资源的浪费。
软件缺陷数据集一般存在数据不平衡问题,即在数据集中有缺陷的模块数量很少,无缺陷模块数量很多。针对数据不平衡的问题,目前已有不少研究,主要包含代价敏感和采样方法。其中代价敏感方法[18]指的是将软件缺陷分为两种类型,两种类型的错误分类成本不同,其中代价敏感方法将软件缺陷分为两种错误分类代价不同的类型,从而使错误分类代价最小。文献[19-20]探索了基于代价敏感的不平衡数据再平衡方法,取得了良好的表现效果,但是存在错误分类成本难以准确制定的不足,对预测精度有较大的影响。采样方法分为欠采样和过采样方法,欠采样方法通过删除多数类样本使得不同类型样本数量基本保持一致。文献[21]首先使用清除正常模块中特征相重叠的模型,对整个数据集进行多次欠采样使数据集再平衡,再使用AdaBoost方法建立预测模型,实验结果表明该方法在AUC(Area Under Curve)和G-mean的评价指标上取得了良好的结果。文献[22]提出了一种基于RUS(Random Under-Sampling)欠采样方法的数据再平衡方法,该模型具有建立简单和高效的优点,但是它的预测效果很大程度上取决于数据集自身的特性和后续数据处理时训练算法的选择。文献[23]提出了一种在软件缺陷数目预测中的针对不平衡现象的方法。文献[7]在SMOTE过采样的基础上对其进行改进提出了SMOTER方法,用于预测目标变量的极值点;该方法普适性强,可与多种的回归模型结合,是一种高效通用的数据平衡化方法。文献[24]考虑了缺陷的软件模块分布不平衡问题,提出了基于SDAEs(Stacked Denoising AutoEncoders)深度学习和集成学习的软件缺陷预测模型,先对软件模块数据集进行深度学习,然后使用集成学习的方法处理软件的不平衡问题,该模型在NASA的软件模块数据集上取得了良好的表现。
1.2 预测软件模块的缺陷数目
文献[25]构建了一个灵活的贝叶斯网络,利用贝叶斯网络进行软件缺陷数目的预测,取得了稳定的输出效果;文献[26]提出了一个基于缺陷状态转移模型的软件缺陷数目预测方法,并且在软件开发实践中得到了验证;文献[27]探索了决策树回归(Decision Tree Regression, DTR)算法在版本内缺陷数目预测和跨版本缺陷数目预测能力,在PROMISE的5个数据集上的实验表明决策树回归算法在平均绝对误差和平均相对误差的评价指标上取得了良好的效果。文献[28]在探索了遗传算法、多层感知器算法、线性回归(Linear Regression, LR)、决策树回归、泊松回归和负二项回归在软件缺陷数目预测上的应用,实验结果表明决策树回归、遗传算法、多层感知器算法和线性回归在平均绝对误差和平均相对误差上取得了更良好的表现,而负二项回归和泊松回归的表现最差。文献[12]探究了在项目内和跨项目的软件缺陷数据集上使用决策树回归、贝叶斯岭回归(Bayes Ridge Regression, BRR)、支持向量回归、线性回归、近邻回归、梯度下降算法对软件缺陷数目进行预测,并使用精确率和均方根误差作为评价指标,结果表明决策树算法在以上的6个算法中的表现最为良好,同时6种回归方法在项目内和跨项目中取得了相似且良好的结果。文献[11,29]提出了一种基于线性、非线性的软件模块缺陷数目预测方法,采用集成学习的方法,将线性方法(线性回归)和非线性方法(决策树回归、支持向量机等方法)的结果进行集成,实验结果表明该方法在软件模块缺陷数目预测的绝对误差和相对误差上取得了称为level I 的良好表现。相比而言,本文首先将不平衡的训练集利用过采样方法进行平衡,然后再利用集成学习方法构建组合预测模型。文献[30]建立了基于负二项式回归的软件模块缺陷数目预测模型,并将其应用到两个大型工业系统中,实验结果表明,该模型预测出了两个工业系统软件模块中,分别包含总缺陷数目71%和92%的20%软件模块,即成功预测出了具有最多软件缺陷数目、最应该被测试的软件模块,但是上述研究没有考虑到软件缺陷预测中,软件缺陷模块分布不平衡问题,预测结果存在偏向性从而不准确。文献[31]提出了一个结合数据过采样、欠采样与AdaBoost.R2算法的软件缺陷数目预测方法。相比文献[31]的方法,本文方法利用平均法的组合策略对个体回归模型进行组合。
2 SMOTENDEL方法
本文针对软件缺陷预测中存在的数据不平衡现象以及单一学习模型导致的过拟合问题,结合过采样和集成学习提出一种软件缺陷数目预测方法——SMOTENDEL。该方法包含过采样、回归和集成3个阶段。首先通过对原始缺陷数据集进行多次过采样形成多个平衡的缺陷数据集,然后利用当前经典的回归算法在各平衡数据集上进行训练,得到若干个个体软件缺陷数目预测模型,将多个个体预测模型进行集成得到一个组合软件缺陷数目预测模型,最后利用该组合预测模型对新的软件模块进行预测。SMOTENDEL方法的基本框架如图2所示。

图2 SMOTENDEL方法过程示意图
其中,Si表示第i次过采样之后的平衡数据集,D代表一种回归算法,Fi表示基于平衡数据集Si训练出的个体软件缺陷数目预测模型,F*表示组合预测模型。
2.1 SMOTEND采样
SMOTE是一种经典的过采样方法,由Chawla等[32]在2002年提出,在不平衡数据的平衡化方面有着不俗的表现,但SMOTE算法只能处理分类领域的数据不平衡问题。文献[7]提出了一种SMOTE的改进算法——SMOTER,用于预测目标变量的极值点。考虑到本文是数值预测问题以及软件缺陷模块在整体软件模块中占比较小的事实,本文改进SMOTER方法,用以解决软件缺陷数据集数据不平衡的问题,称改进的SMOTER方法为SMOTEND(SMOTE for predicting the Number of Defects)。为便于后面的描述,本文给出下列定义:
定义1 正常模块。缺陷数目为零的软件模块。
定义2 缺陷模块。缺陷数目大于零的软件模块。
SMOTEND方法包含两个关键步骤:
步骤1 确定原始数据集中哪些缺陷模块被用于合成新的缺陷模块;
步骤2 计算新的缺陷模块的特征向量和缺陷个数。
SMOTEND首先依据正常模块和缺陷模块的期望比例,确定需要合成的新的缺陷模块的个数。然后,根据需要合成的新的缺陷模块的个数和原始缺陷模块个数确定每个原始缺陷模块需要选择的近邻个数,随后根据软件缺陷模块和近邻的软件缺陷模块构造新的软件缺陷模块。具体步骤如下:
针对步骤1,设正常模块的数量为n,缺陷模块的数量为m,期望得到的缺陷模块与正常模块的比例为ratio。当ratio≤[2×m/n],即需要合成的缺陷模块个数小于原始数据集中缺陷模块个数时,参与合成的原始缺陷模块数目p=ratio×n-m,每个参与合成的原始缺陷模块的选取的近邻个数t= 1;当ratio> [2×m/n]时,即需要合成的缺陷模块个数大于原始数据集中缺陷模块个数时,参与合成的原始缺陷模块数目p=m,每个参与合成的原始缺陷模块的选取的近邻个数t= [ (ratio×n/m) ]。
针对步骤2,用X=(x,y)表示一个软件缺陷模块,其中x是缺陷模块X的特征向量,y是缺陷模块X的软件缺陷数目。对每个参与合成新模块的原始缺陷模块Xi,在其最近邻的k个缺陷模块中(根据文献[7],本文实验中k取5),有放回抽样出t个最近邻模块{Xij|j∈(0,t]},根据模块Xi与抽出模块Xij构造新的软件缺陷模块Xnew,Xnew的特征向量xnew为:
xnew=xi+ rand(0,1) ×(xij-xi)
(1)
记新合成的缺陷模块特征向量xnew与合成新缺陷模块的两个母体模块特征向量(xi,xij)之间的距离分别为d1和d2,则新合成的缺陷模块Xnew的缺陷数目为:
(2)
其中yi和yij分别是缺陷模块Xi和Xi的近邻模块Xij的缺陷数目。
举例说明:如图3所示,根据点(23, 9)和(5, 14)代表的这两个缺陷模块构造新的软件缺陷模块,假设rand(0, 1)取0.2,则新合成的缺陷模块为:(5, 14) + [(23, 9) - (5, 14)]×0.2 = (8.6, 13)
设(5, 14)点的缺陷数目为4,(23, 9)点的缺陷数目为1,求得新合成的点和合成该点的两个母体点之间的欧氏距离分别为d1=3.73和d2=14.94,则新合成的点的缺陷数目为
(3)
四舍五入得点(8.6,13)代表的模块的缺陷数目为2。
SMOTEND伪代码如算法1所示。
算法1 SMOTEND。
输入:软件模块数据集S=[(x1,y1),(x2,y2),…,(xK,yK)];采样后缺陷模块和正常模块数量的期望比例ratio。
1)
fori=1 topdo:
2)
对第i个缺陷模块选择k个最近邻缺陷模块;
3)
forj= 1 totdo:
4)
从k个最近邻中随机抽取第j个最近邻缺陷模块,记作Xij;
5)
根据软件模块Xi,Xij和式(1)构造新的模块的特征向量xij;
6)
根据式(2)得到新的模块的缺陷数目yij;
7)
end for
8)
end for
9)
把上述新生成的缺陷模块集与原缺陷模块集合并,得到一个平衡的数据集S′;
原始不平衡数据通过上述过采样,即根据缺陷模块和最近邻的几个缺陷模块构造新的软件缺陷模块,得到p×t个新的缺陷模块。这种方式能够极大地改善数据的不平衡性。
2.2 回归算法
为了预测软件模块的缺陷数目,本文采用回归算法对平衡化后的数据集进行学习,得到一个学习模型F,根据训练出的模型对待检测的软件缺陷数据集进行预测,可得到软件缺陷数据集的缺陷数目预测结果。已有研究[8-9]表明决策树回归(DTR)模型,贝叶斯岭回归(BRR)和线性回归(LR)这三种回归模型在软件缺陷数目预测中被广泛使用并取得了较好的预测效果,同时这三种模型分属于三种不同类型的回归模型,其中,DTR属于决策树模型,BRR属于概率框架模型,LR属于统计学模型。这三个回归模型的详细信息如下:
决策树回归(DTR) 依据决策树原理,曲线逼近给定的训练集,然后使用训练出的预测模型对测试集进行预测。
线性回归(LR) 对存在线性关系的一个或多个自变量和一个因变量进行线性拟合,使用拟合的模型对测试集进行预测。
贝叶斯岭回归(BRR) 是一种基于贝叶斯算法的回归预测方法,可利用正则参数的对贝叶斯的参数进行先验,规避了主观性的矛盾,结果更具备说服力。
2.3 集成学习
集成学习(ensemble learning)通过构建并结合多个学习器,来完成学习任务。通过集成学习,将预测能力较弱的个体学习器进行结合,可以得到预测能力较强的组合学习器,显著提高泛化性能。集成学习的一般结构为:先产生一组“个体学习器”,再使用某种策略将它们结合起来。集成学习的策略分为两种,一种是同质集成方法,即使用同一种学习方案对数据集的不同子集进行学习,将学习的结果集成在一起;另一种是异质集成方法,使用多种不同的学习方法对同一数据集进行学习,将学习的结果进行集成。本文采用第一种同质集成方法。具体步骤如下:
首先利用2.1节中提出的SMOTEND对原始软件缺陷数据集进行过采样使数据集平衡化,得到一个平衡的软件缺陷数据集,然后利用2.2节中的经典回归算法对平衡数据集进行学习得到一个预测模型。为了避免在单一数据集上学习而导致结果偏差过大,本文提出对多次过采样得到的软件缺陷数据集进行多次回归,得到多个个体软件缺陷数目预测模型,然后,将这多个个体预测模型集成得到一个组合预测模型。本文选择的组合策略为平均法,即将这多个个体模型对待预测软件模块的缺数目的预测值取平均。本文把这种方法称为SMOTENEDEL。SMOTENDEL方法步骤如算法2所示。
算法2 SMOTENDEL。
输入:平衡数据集的个数:n;软件缺陷数据集S;一种回归算法,如决策树回归算法。
输出:组合预测模型F*。
Begin
1)
fori=1 tondo
2)
对S进行SMOTEND过采样得到平衡数据集Si;
3)
基于Si利用回归算法学习出一个个体软件缺陷数目预测模型Fi;
4)
end for
5)
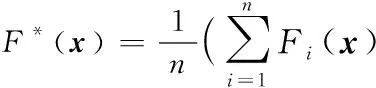
End
经过上述3个阶段,得到一个组合软件缺陷数目回归预测模型F*。利用该组合回归预测模型对新的软件模块进行缺陷数目预测得到新的软件模块的缺陷数目。
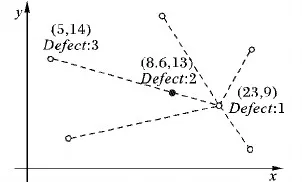
图3 SMOTENDEL示意图
3 实验设置
3.1 实验数据集
本实验根据文献[33],从开源的数据集PROMISE中选取5种实验数据集,其中,软件特征采用CK metrics数据集提供的20个软件缺陷特征。实验数据集的详细信息如表1所示。通过表1可以看出软件缺陷数据集中软件缺陷数目分布有极大的不平衡性,缺陷模块的数量明显远少于正常模块的数量。
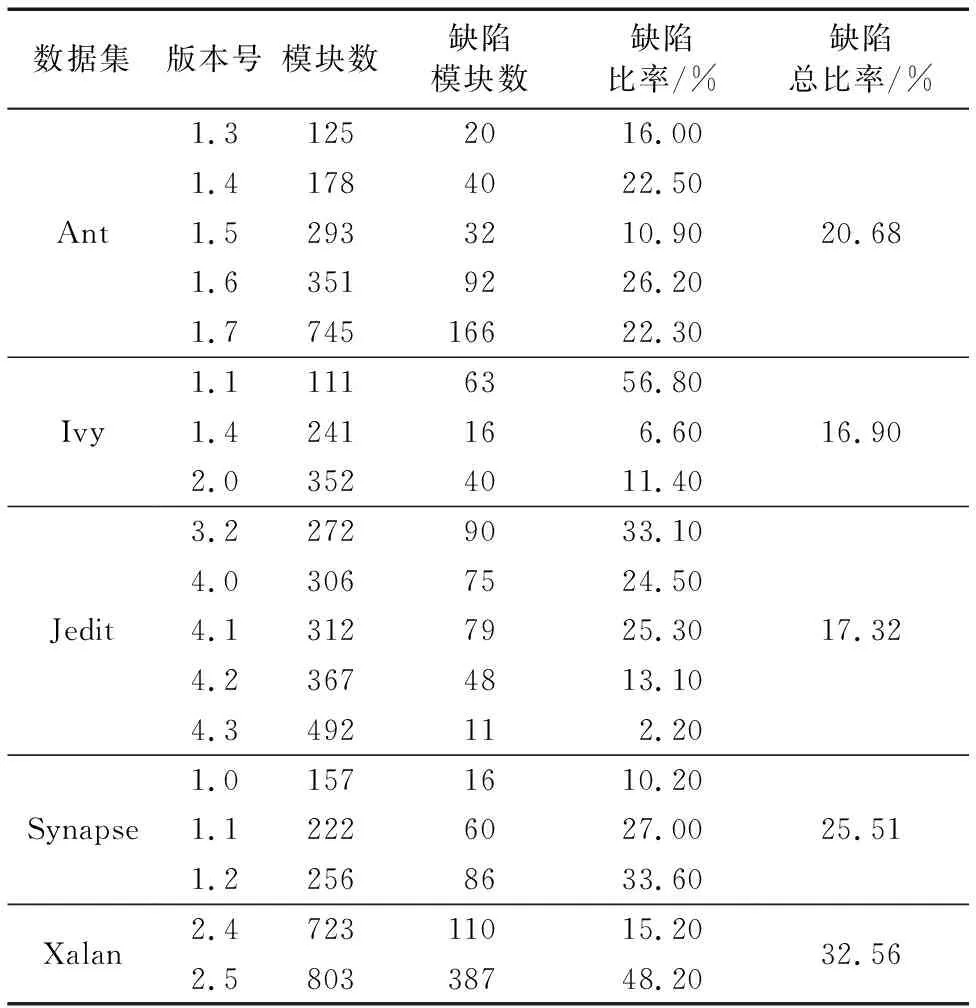
表1 实验中使用的PROMISE数据集
3.2 评价指标
现有的软件缺陷数目预测的文献采用的大多是传统的评价指标。如文献[12]采用了平均绝对误差(Average Absolute Error, AAE)、平均相对误差(Average Relative Error, ARE)、均方根误差(Root Mean Square Error, RMSE)等指标,但这些指标没有考虑到缺陷数目的不平衡性,在本文所研究的问题中具有较大的局限性。比如AAE的定义如下:
(4)
其中:xi,actual代表数据集中第i个软件模块的实际软件缺陷数目,xi,predict代表数据集中第i个软件模块的软件缺陷数目的预测值,n代表数据集中软件模块的个数。
鉴于数据集的极不平衡性,类似于AAE的这类评价指标可能会导致评价过于乐观。软件缺陷数目预测技术的重点是正确地预测出软件缺陷数目多的模块,而这些模块往往处于极少数的地位,它们的预测错误在类似AAE的评价指标中除以庞大的基数,错误会被掩盖。
例如针对Ant.1.3数据集,其有125个模块,正常模块有105个,缺陷数目为1、2、3的模块分别有11、5、4个。假设预测模型预测这20个缺陷模块的缺陷数目都为1,则AAE计算得0.104;假设预测模型预测缺陷数目为3的预测正确了2个,缺陷数目为2的预测正确了3个,缺陷数目为1的预测正确了8个,其他的全预测为正常模块,则AAE计算得0.104,与前者结果相同,但显然后者的预测结果对测试人员帮助更大,故不能使用类似于AAE的这类评价指标作为本研究的评价指标。
文献[13]提出FPA(Fault-Percentile-Average)这个评价指标。FPA是一种专门用于软件缺陷预测领域的评价指标,广泛用于验证预测模型的预测性能,该指标以软件缺陷数目为权重,如果一个模块的软件缺陷数目预测值越大,则该模块的权重就高,对评价指标的影响大。因此在软件缺陷数目多的模块上的预测准确度越高,评价指标表现就越良好。
FPA的计算公式如下:
FPA=M/(n×Y)
(5)
其中:n代表数据集中软件模块个数,Y代表数据集中所有软件模块所具有的缺陷的总数,M是将软件模块按照预测缺陷数目降序排列得到的实际缺陷数目的累加和,具体计算如下。
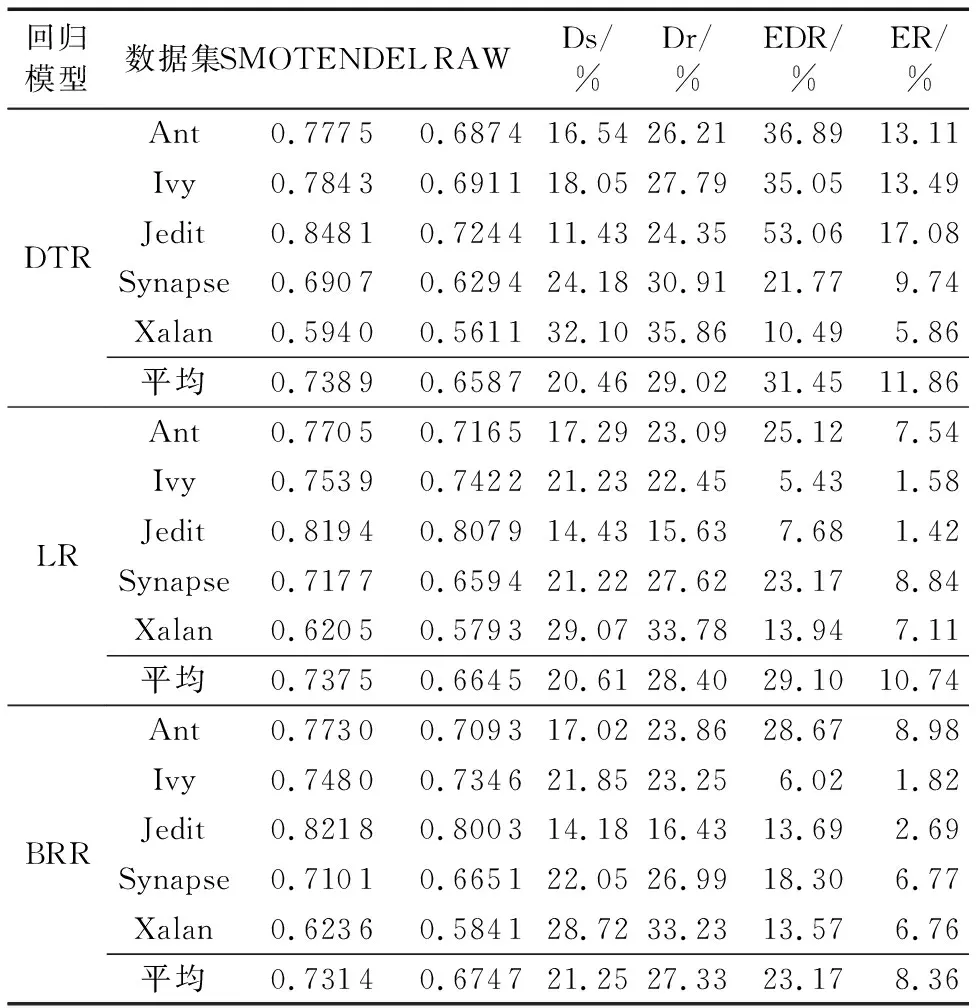
考虑一个含有n个软件模块的数据集,按预测出的缺陷数目升序排列S={S1,S2,…,Sn},即软件模块Sn被预测为拥有最多的软件缺陷。记{y1,y2,…,yn}为对应软件模块实际的缺陷数目。对第m(0 (6) FPA值越大,表明软件缺陷数目预测模型的预测效果越好。本实验中,选取FPA作为评价指标评价软件缺陷数目预测模型效果的评价指标。 为了验证SMOTENDEL预测方法导出的模型在软件缺陷数目预测上的预测性能,需要对模型进行验证。对模型的验证通常有交叉验证法(Cross-Validation)和自助采样法(Bootstrap)两种方法。文献[13]分别探究了k折交叉验证法中,k的取值对验证效果的影响和自助采样法中采样的数目对验证效果的影响,实验结果表明十折交叉验证法在对模型准确性的验证中取得了最优的表现。因此本文采用十折交叉验证法对SMOTENDEL预测方法进行验证。 本文在进行十折交叉检验时,将表1中同一项目不同版本的数据集合并为一个数据集。然后将数据集等分为10组,从中取1组作为测试集,剩下的9组作为训练集,利用SMOTENDEL训练得出软件缺陷数目预测模型,用预测模型对测试集的软件模块进行预测,得到测试集的软件缺陷数目的预测值。依次选择10组中的每1组作为测试集,重复上述步骤可以得到整个软件缺陷数据集的缺陷数目预测值,根据软件缺陷数据集的实际缺陷数目和预测缺陷数目计算FPA值。 为了验证SMOTENDEL方法在软件缺陷数目预测方面的性能,本文提出了以下两个研究问题: 问题1 SMOTENDEL方法中,应该如何设置个体缺陷数目预测模型个数n? 问题2 SMOTENDEL是否能提升软件缺陷数目预测模型的预测性能? 针对3.4节中的问题1,本文分别选择个体缺陷数目预测模型个数n为1,2,3,…,9,10,15,20,…,40和45,对数据集进行SMOTENDEL方法的软件缺陷预测,记录SMOTENDEL方法在不同n值下的表现。 根据实验结果数据绘出如图4所示的FPA-n折线图。由FPA-n折线图可以得出,在使用决策树回归算法的SMOTENDEL方法中,当n取1~5的时候,预测模型的FPA值随着n的增加而增大;当n处于5~15时,模型的稳定性较差,FPA值具有较大的起伏,但整体趋势随着n的增加而增大;当n大于15时,模型的FPA值基本保持高水平和稳定。 图4 采用3种回归模型的SMOTENDEL在5种数据集上的预测性能随个体模型个数n的变化 在使用贝叶斯岭回归算法的SMOTENDEL方法中,当n取1~10的时候,预测模型的FPA值随着n的增加而增大,但在Synapse数据集上有较大起伏;当n处于10~15时,预测模型的FPA值在Jedit和Synapse数据集上随着n的增大先下降后提升,在Ant和Xalan数据集上随着n的增大先提升后下降,在Ivy数据集上随着n的增大而提升;当n大于15时,预测模型的FPA值基本保持高水平和稳定。 在使用线性回归算法的SMOTENDEL方法中,当n取1~5的时候,预测模型的FPA值随着n的增加而增大,但在Ivy和Synapse数据集上有较大起伏;当n处于5~10时,FPA值有小幅度的振荡;当n大于15时,预测模型的FPA值基本保持高水平和稳定。 根据实验结果得出结论:为了使SMOTENDEL方法得到的模型具有良好的性能表现,应该将n设定为15或15以上。考虑到集成学习次数多对计算资源的占用较大,依实验结果,将n设定为15可以在测试资源消耗与性能之间取得较好的平衡。 根据4.1节的结论,实验将预测模型个数n设定为15,使用SMOTENDEL方法对软件缺陷数据集进行学习,导出软件缺陷数目预测模型,使用十折交叉验证法对预测模型进行验证,使用FPA指标进行评价。FPA的最高值,即所有软件模块缺陷数目全部预测正确,分别为0.931 6,0.957 1,0.957 6,0.911,0.874 8。对各个数据集分别采用SMOTENDEL预测方法和原始预测(RAW)方法得到的FPA值以及平均值(Average)如表2所示,其中ELEVATION RATIO(ER)为SMOTENDEL方法相对于直接进行回归预测方法的FPA提升率。实验结果表明,在FPA绝对值提升率上,基于DTR决策树回归的SMOTENDEL方法相对于直接回归的传统方法有着平均7.68%的提升,基于线性回归(LR)和贝叶斯岭回归(BRR)的SMOTENDEL方法相对于传统直接回归的方法有着平均3.31%和3.38%的提升。 表2 5个数据集在3个回归模型下的FPA值以及FPA提升率 此外,本文还将SMOTENDEL和RAW方法与最优模型(即将所有软件模块缺陷数目全部预测正确)进行了比较, SMOTENDEL_DIFFERENCE (Ds)、RAW_DIFFERENCE(Dr)表示SMOTENDEL、RAW与最优模型FPA值相差的百分比,ELEVATION RATIO OF DIFFERENECE (ERD)为SMOTENDEL与最优模型FPA值相差的百分比相较于RAW与最优模型FPA值相差的百分比的提升率。 在与完全预测正确的结果的FPA值比较中,基于决策树回归的SMOTENDEL方法与完全预测正确的FPA值相差20.46%,相比传统直接回归方法有着近31.45%的提升,基于LR线性回归和BRR贝叶斯岭回归的SMOTENDEL方法与完全预测正确的FPA值相差分别为20.65%和20.67%,相比传统直接回归方法也有着15.07%和16.05%的提升。 图5为使用盒须图对SMOTENDEL方法在各个数据集上的FPA表现进行的描述,盒须图包含最大值、上四分位点、中位数、平均数、下四分位点和最小值,能够有效地对比SMOTENDEL方法和传统预测方法在FPA上的表现。 根据图5可以发现,在分别使用决策树、线性回归、贝叶斯岭回归的情况下,本文提出的SMOTENDEL软件缺陷预测方法较传统、不作数据处理的回归预测方法在四分位点上等多个指标上均取得了明显的提升。 图6对基于三种回归方法的SMOTENDEL软件缺陷数目预测方法得到的FPA提升率进行对比分析。 由图6可知,决策树回归(DTR)下的SMOTENDEL方法得到的FPA值的提升率最为明显。线性回归(LR)和贝叶斯岭回归(BRR)在中位数、最大最小值上没有明显的差异,贝叶斯岭回归较线性回归在四分位点上有着略微的优势。 根据实验结果得出结论:SMOTENDEL方法能够有效地提升软件缺陷数目预测的效果。基于决策树算法的SMOTENDEL方法具有最良好的性能表现。 图5 对5个数据集分别采用和不采用SMOTENDEL方法进行预测得到的FPA值 图6 对5个数据集采用3种回归模型的SMOTENDEL方法的FPA提升率 针对软件缺陷数目预测问题,本文提出了一种基于过采样和集成学习的SMOTENDEL方法。SMOTENDEL方法首先对不平衡的软件缺陷数据集进行多次过采样得到多个平衡数据集,然后对这多个平衡数据集进行回归预测得到对应的个体预测模型,随后利用集成学习的方法将这多个个体预测模型集成,得到一个组合预测模型,最后利用该组合预测模型对待预测的软件模块进行预测,得到其软件缺陷数目。本文使用 FPA作为评价指标,利用十折交叉验证法对该方法进行检验。实验结果表明:1)SMOTENDEL方法能够有效提高软件缺陷数目预测模型的性能,其中基于决策树回归的预测模型取得了最优的性能表现;2)集成学习次数n选择为15时能够同时占有较少的计算资源而获得良好的性能表现。 本文所选择的数据集特征全部来源于同一类Chidamber and Kemerer (CK) metrics,这种类型的软件缺陷数据主要来自使用面对对象语言编写的软件系统,在1994年创建并经历了时间的考验,在软件缺陷预测技术上被普遍使用并取得了良好的表现,但是由于创建时间过早,创建时里面只有SmallTalk和C++两种语言,在现在计算机语言飞速发展的如今,使用CK软件缺陷数据得到的预测模型可能并不完全满足于现代工业界的软件缺陷预测需求。在未来会使用多个不同种类的数据集来验证SMOTENDEL方法的普遍性,使其更好地服务于现代工业界。 [24] TONG H, LIU B, WANG S. Software defect prediction using stacked denoising autoencoders and two-stage ensemble learning [J]. Information and Software Technology, 2017,96: 94-111. [25] OKUTAN A, YILDIZ O T. Software defect prediction using Bayesian networks [J]. Empirical Software Engineering, 2014, 19(1): 154-181. [26] WANG J, ZHANG H. Predicting defect numbers based on defect state transition models [C]// ESEM ’12: Proceedings of the ACM-IEEE International Symposium on Empirical Software Engineering and Measurement. New York: ACM, 2012: 191-200. [27] RATHORE S S, KUMAR S. A decision tree regression based approach for the number of software faults prediction [J]. ACM SIGSOFT Software Engineering Notes, 2016, 41(1): 1-6. [28] RATHORE S S, KUMAR S. An empirical study of some software fault prediction techniques for the number of faults prediction [J]. Soft Computing, 2017, 21(24): 7417-7434. [29] RATHORE S S, KUMAR S. Towards an ensemble based system for predicting the number of software faults [J]. Expert Systems with Applications, 2017, 82: 357-382. [30] OSTRAND T J, WEYUKER E J, BELL R M. Predicting the location and number of faults in large software systems [J]. IEEE Transactions on Software Engineering, 2005, 31(4): 340-355. [31] YU X, LIU J, YANG Z, et al. Learning from imbalanced data for predicting the number of software defects [C]// ISSRE ’17: Proceedings of the 2017 IEEE 28th International Symposium on Software Reliability Engineering. Washington, DC: IEEE Computer Society, 2017: 78-89. [32] CHAWLA N V, BOWYER K W, HALL L O, et al. SMOTE: synthetic minority over-sampling technique [J]. Journal of Artificial Intelligence Research, 2002, 16(1): 321-357. [33] YANG X, TANG K, YAO X. A learning-to-rank approach to software defect prediction [J]. IEEE Transactions on Reliability, 2015, 64(1): 234-246.3.3 十折交叉验证法
3.4 研究问题
4 实验结果分析
4.1 研究问题1

4.2 研究问题2
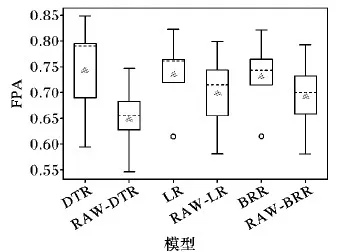
5 结语

