基于流网络的流式计算动态任务调度策略
李梓杨,于 炯,,卞 琛,鲁 亮,蒲勇霖
(1.新疆大学 信息科学与工程学院,乌鲁木齐 830046; 2.新疆大学 软件学院,乌鲁木齐 830008)
0 引言
随着互联网技术和信息产业的不断发展,全球数据量呈几何式增长,截止2015年全球数据总量达8.61 ZB,并预计到2020年全球数据总量将超过40 ZB[1],同时,通过移动互联、社交媒体、全球定位系统(Global Positioning System, GPS)导航等新的服务模式,大数据[2]产业及相关服务已经深入到人们生活的方方面面,也为互联网企业带来巨大收益。然而随着数据价值的时效性变得越来越明显,集群必须以毫秒级的延迟从大规模数据中提炼出有价值的信息,才能满足用户对数据分析的实时性要求,大数据流式计算[3]应运而生。流式计算具有实时性、易失性、无序性、无限性和突发性的特征[4],能够提供高效的数据分析服务,已在交通预警、实时推荐等对实时性要求高的场景中得到广泛应用;但流式计算的技术发展也面临着一些挑战,多样的输入数据源和不断变化的输入数据速率对集群的负载承受能力和可伸缩性提出了更高的要求,特别是输入速率的急剧上升会给集群造成很大的负载压力,如果应对不力就会造成数据元组被阻塞或丢弃,甚至出现节点崩溃等现象,影响计算的实时性和准确性。
流式计算的发展诞生了不同特点的数据流处理平台,Apache Flink[5-9]是新兴的目前产业界应用最广泛的平台之一。与Storm[10]平台相比,Flink能提供Exactly-Once的可靠性计算[11]以及更完善的背压机制[12],并支持用户定义的时间窗口[13],但在输入速率上升阶段的吞吐量仍有待提高,因此,本文提出基于流网络模型的动态任务调度(Flow Network based Dynamic Dispatching, FNDD)策略。该策略将流式计算拓扑转化为流网络模型,通过容量检测算法和最大流算法实现流式计算平台的动态任务调度。经实验验证得出,该策略对不同作业类型的优化效果有较明显的区别:其中集群在WordCount作业中的吞吐量平均提高了29.41%,在TwitterSentiment作业中的吞吐量平均提高了16.12%,在TeraSort作业中的吞吐量平均提高了38.29%。
1 相关工作
为了解决流式计算中输入速率急剧上升导致数据元组被阻塞或丢弃,进而影响计算的实时性和准确性的问题,必须提出一种在输入速率上升阶段的任务调度策略,使其能够根据节点的处理能力合理地负载分配,并根据实际情况动态变化,从而在保证低延迟的同时提高吞吐量。
针对输入数据的速率急剧上升导致集群的负载压力增大的问题,现有的研究成果大多只关注节点内的计算开销而忽略了节点间的传输开销,且大多不适用于Flink平台。文献[14]研究发现:集群拓扑结构和节点内缓存大小对任务的计算延迟和吞吐量有较大的影响,提出通过调整缓冲区的大小以及动态链接(Chain)部分算子的思想,在满足计算延迟约束的前提下尽可能提高吞吐量;但其同步的性能监控策略产生了较大的时间开销,导致该算法不能应用于大规模集群。文献[15]在文献[14]的基础上提出异步的节点性能监控策略,通过性能监控(Quality Monitor, QM)进程和性能反馈(Quality Reporter, QR)进程异步监控节点的性能数据,有效降低了作业执行的时间开销,并将该算法部署于200个节点的大规模集群,但该策略监控的性能指标较单一,且未考虑节点间的传输开销。文献[16]在文献[15]的基础上建立数学模型,依据QR和QM收集的性能数据算出每个算子的合理并行度,并根据计算结果进行动态调整,从而在满足计算延迟约束的前提下有效提高集群的吞吐量,但其数学模型过于复杂,集群在输入速率急剧上升阶段的响应速度无法满足实际需求。文献[17]提出基于有状态数据分片调度策略的数据流系统ChronoStream,通过实施高效的状态数据管理计划,使节点在横向和纵向上均实现可伸缩性,但其分片的调度策略产生了较高的时间开销。文献[18]提出一种可扩展的数据流处理系统StreamCloud,通过整合高效的任务调度和负载均衡策略,实现对用户透明的数据流查询功能,其思想被用于改进Borealis平台并取得了很好的效果。文献[19]根据集群拓扑中关键路径上的性能感知数据,在保证计算实时性的前提下尽可能降低能耗,但未考虑节点内存、网络传输等其他性能指标对集群性能的影响。文献[20]提出用计算延迟作为综合评估节点性能的指标,通过实施节点间的动态负载均衡策略降低任务的计算延迟。
针对上述文献中存在的数据流任务调度策略多关注节点内的计算开销,而忽略节点间传输开销的问题,本文的主要工作有:
1)通过定义流式计算的有向无环图(Directed Acyclic Graph, DAG)中每条边的容量与流量值,将其转化为流网络模型,兼顾节点的计算开销与边的传输开销。
2)提出容量检测算法,在计算延迟阈值的约束下检测每个节点的最高负载,并将其记为对应输入边的容量,从而构建流网络模型。
3)在流网络模型的基础上提出最大流算法,在输入速率上升阶段根据流量与容量的关系进行合理的负载分配,在满足延迟约束的前提下提供尽可能高的吞吐量,实现计算资源的最大化利用。
2 流网络模型
通过动态调度策略合理分配新增的计算负载,最大化利用计算资源,才能在输入速率上升阶段有效提高集群的吞吐量。如果将数据源的输入速率作为期望吞吐量(Expected Throughput, ET),而集群当前时刻实际处理数据的速率为实际吞吐量(Actual Throughput, AT),则动态调度策略的目的是通过优化节点间的调度和负载分配方式,使集群的实际吞吐量满足不断上升的期望吞吐量。最大流算法通过建立流网络模型,寻找一条从源点到汇点的优化路径,并沿着优化路径的方向提高计算负载,从而提高整个集群的实际吞吐量。
2.1 流式计算的结构
在大数据流式计算中,通常将用户定义功能(User Define Function, UDF)作为一系列算子,待处理的数据元组从源点发出,依次经过每个算子的处理,最终将计算结果在汇点持久化。其中数据源点往往可以有多种多样的数据产生方式,数据汇点可以是Hadoop分布式文件系统(Hadoop Distributed File System, HDFS)等数据存储平台或直接将处理结果反馈给用户,中间的一系列算子共同实现了用户定义的业务功能。
在分布式数据流处理系统中,为了提高集群的性能以保证计算的实时性,通常将同一个算子映射到不同的计算节点上,使它们能够分别同时完成相同的计算任务,从而提高任务的执行效率。如图1所示,O1、O2、O3是任务中依次处理数据的3个算子,被分别映射到v1、v2等7个计算节点上,算子之间数据传输被映射到计算节点间的通信链路上,这样就形成了流式计算的DAG拓扑;但传统的流式计算模型大多只关注节点内部的计算延迟,而忽略了节点间边的传输延迟。事实上集群往往受限于计算和传输共同导致的时间开销,而难以实现低延迟和高吞吐量兼得,急剧上升的计算负载会导致数据被阻塞而产生更高的延迟,因此,有效的任务调度策略必须兼顾节点内部的计算开销和节点间的传输开销,并在满足延迟约束的前提下尽可能提高实际吞吐量。
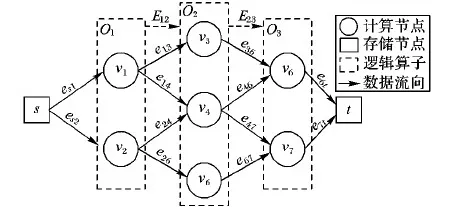
图1 流式计算模型
2.2 数据流网络
通过定义DAG拓扑中每条边上允许数据传输的最大速率为该边的容量,而实际传输的速率为流量,就形成了对应的流网络模型。
定义1 数据流网络。如图2所示,设有向无环图G=(V,E),其中V={v1,v2,…,vn}是图中所有节点的集合,s∈V是流网络的源点,t∈V是汇点,E={(vi,vj)|i,j∈[1,n],n=|V|}是所有边的集合,(vi,vj)是从节点vi向vj传输数据的边。其中每条边(vi,vj)∈E都有c(vi,vj)≥0表示边(vi,vj)允许数据传输速率的最大值,也称为边(vi,vj)的容量,而实际从节点vi向vj传输数据的速率是边(vi,vj)的流量,记为f(vi,vj)。
根据定义1可知,对于流网络中任意一条边(vi,vj)∈E,都有0≤f(vi,vj)≤c(vi,vj),即在任意边上传输数据的速率不能超过其容量的限制,这称为容量限制定律;同时,对于任意的节点vi∈V-{s,t},其所有的前驱节点记为vj,后继节点记为vk,则满足:
(1)
即对于流网络中任意一个计算节点,受其内部计算开销的影响,在任意时刻数据流入该节点的速率总是大于或等于数据流出该节点的速率,这称为流量限制定律。实际上,流网络中任意边(vi,vj)的容量值c(vi,vj)的大小都与节点vj及其后继的数据处理能力有关:节点vj的处理能力越强、局部吞吐量越大,则c(vi,vj)越大;反之c(vi,vj)越小。同时,每条边的容量大小还与节点间的网络传输速率、计算延迟约束等多种因素有关,而流量f(vi,vj)是在任务运行中的某一时刻,实际从节点vi向vj传输数据的速率,是随着时间不断变化的。
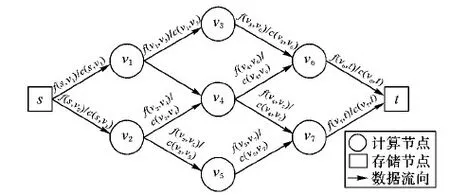
图2 数据流网络图
定义2 流。设G=(V,E)是一个流网络,其中s为源点,t为汇点,则G的流是一个实值函数f:V×V→R。其流量的大小为:
(2)
流网络中一个流的流量是数据从源点流出速率的和也是数据流入汇点的速率的和,是集群实际处理数据的速率,即当前时刻的实际吞吐量,其中流量最大的一个流是G的最大流,记为fmax。
定义3 增进网络。如图3所示,设流网络G=(V,E),则其对应的增进网络为Gf=(Vf,Ef),其中对于所有的节点vi∈V都有vi∈Vf,对于所有的边(vi,vj)∈E,在增进网络中对应的容量cf(vi,vj)为:
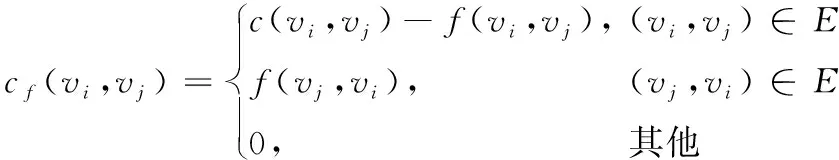
(3)
其中:E是原网络中边的集合;c(vi,vj)是原网络中边(vi,vj)的容量;f(vi,vj)是原网络中边(vi,vj)的流量。
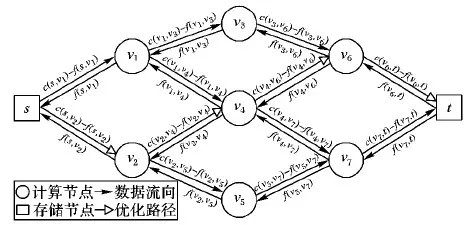
图3 增进网络图
根据定义3可知,增进网络主要反映了对应原网络中流量可能提升的空间,其中存在与原网络中反向的边,是因为在优化负载分配的过程中,有可能减少一些边的流量而增加到另外一些边上,实现提升整个集群吞吐量的目的,因此,在增进网络中寻找一条优化路径就可以按照其方向提高原网络的流量。

|fp|=cf(p)=min {cf(vi,vj)|(vi,vj)∈P}
(4)
其中cf(vi,vj)是增进网络中边(vi,vj)的容量。
优化路径是提升原网络流量的一个方案:当期望吞吐量上升时,系统通过在增进网络中寻找一条优化路径,并在原网络中将优化路径上的边的流量分别增大|fp|,就得到一条流量为|f|+|fp|的流。通过这样反复迭代,不断在增进网络中寻找新的优化路径就可以不断提高集群的实际吞吐量。
定理1 最大流定理。设流网络G=(V,E),Gf是其对应的增进网络,f是流网络G的一个流,则以下两个条件是互相等价的:
条件1f是G的最大流,即|f|=|fmax|;
条件2 增进网络中不存在任何优化路径。
证明
证毕。
根据定理1可知,流网络达到最大流当且仅当对应的增进网络中不存在任何优化路径,即只要在增进网络中能找到一条新的优化路径,就可以沿着优化路径的方向提升原网络的流量,这为提出最大流算法提供了模型的支撑。
3 最大流算法
基于流网络模型及其相关定义,FNDD策略先通过容量检测算法确定DAG拓扑中每条边的容量值,将其转化为流网络模型。在输入数据速率上升阶段,当期望吞吐量大于集群的实际吞吐量时,首先根据流网络中每条边上容量与流量的差值,通过最大流算法计算对应的增进网络并寻找一条优化路径,再通过沿着优化路径的方向提升原网络的流量,实现在限定的延迟约束下提升实际吞吐量的目标。
3.1 容量检测算法
只有将流式计算的DAG拓扑转化为流网络模型,才能使用最大流算法提高集群的实际吞吐量,因此在限定的延迟约束下确定每条边的容量大小,对最大流算法的执行效果至关重要。容量过大会导致节点在实际环境中无法及时处理数据,使其在缓存中被滞留而延迟加长,甚至因内存耗尽导致节点崩溃,而容量过小则无法充分利用计算资源。
为了在限定的延迟约束下获得尽可能高的吞吐量,必须在任务启动后,首先通过容量检测算法确定每条边的容量值,从而为最大流算法的执行建立流网络模型。算法在限定计算延迟阈值的前提下不断提高期望吞吐量,当实际的延迟远小于设定的阈值时,以恒定的步长提高期望吞吐量;当实际的延迟略小于或等于阈值时,将当前的期望吞吐量作为节点对应输入边的容量。当所有边的容量值都确定后,就完成了流网络模型的构建。容量检测算法的具体执行过程如算法1所示。
算法1 容量检测算法。
输入:集群拓扑G′,延迟约束的阈值θ,期望吞吐量ET。
输出:数据流网络G。
1)
foreache∈G.E
2)
e.c← ∞;
/*将DAG中所有边的容量初始化为无穷大*/
3)
end foreach
4)
varnum← |G.E|;
/*用变量num记录尚未确定容量值的边的数目*/
5)
whilenum>0
6)
G.s.start(ET,60);
/*作业开始执行的第1 min,以ET的速率向集群输入数据*/
7)
foreachv∈G.V
/*依次遍历流网络中的每一个节点*/
8)
if avg(v.f-v.d)-θ≤εthen
/*寻找平均计算延迟略小于或等于阈值θ的节点*/
9)
v.pe.c←ET;
/*将当前节点输入边的容量设为当前的期望吞吐量*/
10)
num--;
/*待确定容量值的边的数目减1*/
11)
end if
12)
end foreach
13)
ET←ET+10 000;
/*提升期望吞吐量,准备进入下一次迭代*/
14)
end while
15)
returnG;
如算法1所示,首先将拓扑中所有边的容量设为无穷大(第1)~3)行)并记录拓扑中边的数目(第4)行),然后以用户设定的初始ET从源点开始输入数据(第6)行),每经过60 s统计一次平均计算延迟并寻找所有延迟略小于或等于阈值θ的节点,将当前的ET作为其对应输入边的容量并将未确定容量的边数减1(第8)~11)行),最后判断如果拓扑中还有未确定容量值的边,则提高ET的大小并进入下一次迭代(第13)行),直到所有边都确定容量为止。这样就将流式计算的DAG拓扑转化为对应的流网络模型,同时保证当每条边都满足容量限制定律时,计算延迟应当不超过设定的延迟阈值,为最大流算法提供了模型的支撑。
3.2 最大流算法
根据流网络及其相关定义,在容量检测算法确定每条边的容量大小后,当期望吞吐量大于实际吞吐量时,就可以通过最大流算法增加一些边的流量以提高整个集群的实际吞吐量:首先根据定义3计算流网络对应的增进网络,然后用图的广度优先搜索算法在增进网络中寻找一条优化路径P,再根据定义4计算优化路径所对应的增量|fp|,最后在原网络中沿着优化路径的方向提高每条边的流量,并将提升后的流量记为:
(5)
则整个流网络的流量大小提升至|f|+|fp|,其中f(vi,vj)为原网络中边(vi,vj)的流量。
根据增进网络、优化路径和流网络中每条边上流量与容量的大小关系,当期望吞吐量大于集群的实际吞吐量时调用最大流算法提升集群的吞吐量。最大流算法的具体执行过程如算法2所示。
算法2 最大流算法。
输入:流网络G;期望吞吐量ET。
输出:提升后的流量|f|。
1)
Gf.V←G.V;
/*根据定义3,原网络的节点集合就是
增进网络的节点集合*/
2)
foreach (vi,vj)∈G.E
3)
cf(vi,vj) ← (vi,vj).c-(vi,vj).f;
4)
cf(vi,vj) ← (vi,vj).f;
5)
end foreach
/*根据定义3计算增进网络中对应边的容量*/
6)
P← BFS(Gf,s,t);
/*通过广度优先搜索在增进网络中
寻找一条从源点s到汇点t的优化路径*/
7)
whileET>|G.f| andP!=∅
/*当期望吞吐量大于流量且
增进网络中存在优化路径时,进入提升网络流量的迭代过程*/
8)
|fp| ← min{cf(vi,vj)|(vi,vj)∈P};
/*计算优化路径对应的增量*/
9)
foreach edge(vi,vj)∈P
10)
if (vi,vj)∈G.E
11)
(vi,vj).f← (vi,vj).f+|fp|;
12)
else if (vj,vi)∈G.E
13)
(vj,vi).f← (vj,vi).f-|fp|;
14)
end if
/*根据式(5),沿着优化路径的
方向提升原网络的流量*/
15)
end foreach
16)
|G.f| ← |G.f|+|fp|;
/*记录新的流网络的
流量大小*/
17)
P← BFS(Gf,s,t);
/*寻找新的优化路径并
进入下一次迭代*/
18)
end while
19)
return |G.f|;
算法先根据流网络构建对应的增进网络(第1)~5)行)并在增进网络中用广度优先搜索算法寻找一条优化路径(第6)行),如果存在优化路径就进入对原网络的迭代优化过程:首先根据定义4计算优化路径对应的增量(第8)行),再根据式(5)提高原网络中对应边的流量(第9)~15)行),最后记录新的网络流量并寻找一条优化路径进入下一次迭代。
根据定理1可知,只要增进网络中存在优化路径就意味着原网络的流量仍有提升的空间,沿着优化路径的方向就可以提升集群的吞吐量,使实际吞吐量不断满足期望吞吐量的要求。直到增进网络中不存在任何优化路径时,集群中所有节点都处于满负荷工作状态,此时计算资源得到最大化利用。
3.3 参数影响与代价评估
阈值θ是FNDD策略中唯一的参数,是由用户定义的作业中允许每个数据元组的最大计算延迟,取值过小会导致集群能承受的负载过低,而取值过大则无法满足作业的实时性要求。实际上θ的取值与以下三个因素有关:其一,与作业本身的复杂度有关,作业的复杂度越高则θ的取值应越大,反之可以设定较小的θ值;其二,与实际应用中对服务质量的要求有关,用户对计算的实时性要求越高θ的取值应该越小;其三,与集群的实际规模和性能有关,集群的节点数越多、计算能力越强则计算延迟越低,θ的取值也可相应减小。这三个因素都是在算法设计和实现过程中无法掌握的,因此由用户根据应用中作业和集群的实际情况设定,4.2节通过实验得出在每种作业类型下推荐的参数值范围,供用户参考。
在算法的复杂度方面,容量检测算法的时间复杂度为T(n)=O(|V|×|E|),其中|V|和|E|分别为流网络中节点和边的数目,目前Flink平台在实际应用中的最大集群规模约1 500个节点[21],节点间边的数目与实际应用中集群的拓扑结构和作业的部署模型有关,且|E|≤|V|×k/2,其中k与任务的并行度和集群的拓扑结构有关,当k=10时,|E|≤1 500×10/2=7 500,因此容量检测算法的时间开销在合理可接受的范围内。另外算法收敛的速度还与期望吞吐量递增的步长有关,设定合适的步长能够使整个流网络更快地趋于稳定。最大流算法的执行效率与在增进网络中寻找优化路径的算法密切相关,使用广度优先搜索算法选择优化路径的时间复杂度为T(n)=O(|V|+|E|)=O(|E|)。最大流算法的执行还与提升的流量有关:设最大流为|fmax|,则如果每次迭代增加1 tuple/s时算法达到最高时间复杂度为T(n)=O(|E|×|fmax-f|),其中|f|是集群当前的流量,这在实际应用中是不太可能出现的。由于流式计算集群的节点以及节点间通信链路的数目都不是很高,因此整个FNDD策略的时间复杂度是可接受的。在空间复杂度上,流网络模型只在DAG拓扑的基础上改变了每条边的权值而没有带来新的空间开销,而增进网络与流网络的空间复杂度是相等的,同时实验验证了FNDD策略对集群性能的优化远大于算法本身的开销,因此算法在时间和空间复杂度上都是可行的。
4 实验结果与分析
Apache Flink是目前应用中最重要的数据流处理平台之一,承担着许多企业的实时计算任务。为了使FNDD策略能够更好地在实践中得到应用,在Flink平台中实现了最大流和容量检测算法,并针对不同作业类型的基准测试选定了能够使算法达到最优效果的参数值,最后在相同环境下分别从吞吐量、计算延迟以及内存占用率三个维度将FNDD策略与原系统的调度策略形成对比,验证了算法的优化效果。
4.1 实验环境
实验搭建的集群由15台普通物理PC机组成,分别由Kafka作为数据源点,根据实验设置以不同的速率向集群输入数据,用TaskManager节点构建整个计算拓扑,将计算结果保存在HDFS中并统计相关性能指标,以Zookeeper作为集群的同步协调节点负责分布式节点间的信息同步。集群中所有节点都连接在一个独立的专用网络中,与公共网络隔离,不产生任何非必要的额外传输开销。具体的节点分布情况如表1所示。
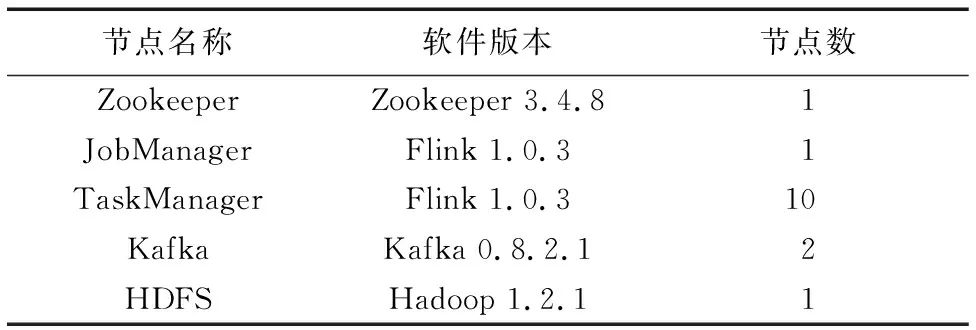
表1 集群节点分布信息
集群中所有节点采用相同的软硬件配置环境,配置参数如表2所示。每个TaskManager只开启一个TaskSlot,即参数taskmanager.numberOfTaskSlots=1,因此作业的并行度最大开启到10,即parallelism.default=10。这样可以充分利用计算资源,并验证FNDD策略在不同计算节点之间进行作业调度的优化效果,避免在同一个节点内的不同进程间进行负载分配。

表2 节点配置参数
实验分别执行了WordCount、TwitterSentiment和TeraSort三个标准的基准测试,首先通过参数调整实验分别确定了在每种类型的作业中,能够使算法达到最优效果的参数θ的取值,再分别将FNDD策略与Flink系统原生的调度策略进行对比,验证了算法的优化效果。
4.2 参数调整实验
为了确定参数θ的取值范围,使集群达到最高实际吞吐量,即FNDD策略达到最好的优化效果,首先在不同的作业类型下开展参数调整实验。实验选取的3个基准测试分别代表了流式计算3种不同类型的作业:WordCount用于统计英文单词出现的频次,其计算复杂度低且对内存的占用率较低,但对CPU资源的占用率较高;TwitterSentiment是Twitter公司开发的对用户发布的推文进行实时情感分析的作业,其计算相对复杂且对CPU和内存资源的占用率都比较高;TeraSort是对大规模数据进行分布式排序的作业,计算复杂度最高,作业执行过程中产生大量状态数据会占用内存资源且节点间有频繁的数据交互。
根据对原系统的采样结果可知:3个作业执行中的计算延迟大多分布在0.1 ms~0.2 ms,最高实际吞吐量不超过90 000 tuple/s,因此,为了选取参数θ更精确的取值以获得最高的实际吞吐量,实验将期望吞吐量设为95 000 tuple/s,θ在0.1 ms~0.2 ms以0.01为步长依次取值,得到如图4所示的实验结果。
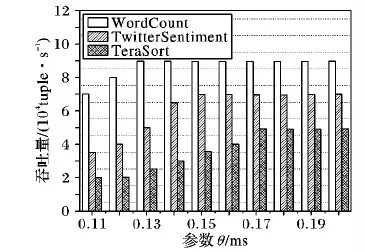
图4 不同参数的吞吐量对比
根据容量检测算法的核心思想,当算法在不同的参数取值下得到非常相近的吞吐量时,实验总是选择尽可能小的θ取值,通过限定较低的计算延迟约束来提高计算的实时性。根据图4可知,WordCount作业在θ取0.13 ms~0.20 ms时都能达到最高吞吐量89 500 tuple/s,因此选择最小值θ=0.13 ms。同理可得,TwitterSentiment作业能达到最高吞吐量69 700 tuple/s的最小θ值为0.15 ms,TeraSort作业能达到最高吞吐量49 000 tuple/s的最小θ值为0.17 ms。
为了进一步验证参数θ的取值,在获得高吞吐量的同时尽可能降低延迟,实验检测在不同参数值下的计算延迟并进行对比。根据图4可知,计算复杂度最高的TeraSort作业的最高吞吐量平均可达5 000 tuple/s。为了避免过高的输入速率造成数据阻塞而影响计算延迟的检测结果,实验将3个作业的期望吞吐量固定在50 000 tuple/s,分别在不同的参数下执行作业并统计实际的平均计算延迟,得到如图5所示的实验结果。这与吞吐量对比实验中得到的结果是基本一致的,WordCount作业在θ=0.13 ms时达到最低的延迟,TwitterSentiment作业在θ=0.15 ms时达到最低的延迟,TeraSort作业在θ=0.17 ms时达到最低的延迟。
综上所述,3种类型作业的参数取值都在0.1 ms~0.2 ms,根据图4和图5可知,当计算比较简单时其延迟相对较低,则参数取值一般不超过0.15 ms,当计算任务相对复杂时θ的取值应有所增大,一般在0.15 ms~0.17 ms。而排序类作业计算复杂且内存占用率高,因此参数θ的取值一般在0.17 ms以上。通过分析在不同作业类型下的实验结果,确定了参数θ的合理取值范围,能够使集群达到最高实际吞吐量,FNDD策略实现较好的优化效果。
4.3 对比实验与分析
根据参数调整实验得到的实验结果,分别确定了参数θ的合理取值范围,因此对比实验使用该取值分别执行WordCoud、TwitterSentiment和TeraSort作业,以验证FNDD策略的优化效果。
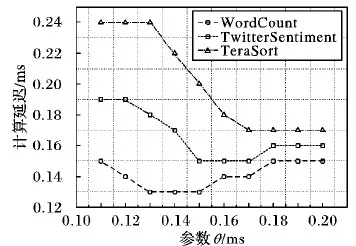
图5 不同参数的计算延迟对比
其中WordCount作业的计算本身并不复杂,但其作业执行过程中对节点的CPU占用率较高,是常用的测试集群性能的标准基准测试。由图4可知,WordCount作业的最高吞吐量约90 000 tuple/s。为了验证FNDD策略在输入速率上升阶段的优化效果,实验将初始的期望吞吐量设为40 000 tuple/s,每经过1 min将期望吞吐量提高10 000 tuple/s,直至期望吞吐量达到90 000 tuple/s后持续输入3 min,之后期望吞吐量逐步下降,并从吞吐量和计算延迟两个维度将FNDD策略与原系统调度策略的性能形成对比。
如图6所示,随着期望吞吐量的逐步上升,Flink原系统在约68 000 tuple/s时达到其吞吐量的瓶颈,当期望吞吐量继续上升时有数据元组被阻塞而延迟加长,在未开启检查点机制时甚至出现数据丢弃的现象。通过使用FNDD策略,当期望吞吐量不断上升时,算法根据优化路径的方向合理分配新增的计算负载,使集群的实际吞吐量从68 000 tuple/s提高至88 000 tuple/s,平均提高了29.41%,基本满足期望吞吐量的要求。另外通过实验发现参数θ取0.13 ms或0.15 ms时都能取得比较好的优化效果,但当θ=0.15 ms时在期望吞吐量上升阶段的优化效果更显著,最终两种情况都稳定于几乎相同的吞吐量值,但在计算延迟上有比较明显的区别。
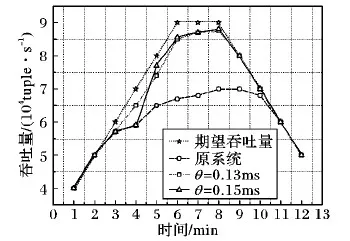
图6 WordCount吞吐量对比
图7为汇点每接收到10 000 tuple时记录一个延迟时间并持续12 min得到的实验结果:在原系统中由于部分节点无法及时处理数据,导致部分元组被阻塞而计算延迟加长,而经过FNDD策略优化后集群的计算延迟有较明显的下降。当θ=0.13 ms时虽然在输入速率上升阶段的实际吞吐量上升较慢,但比θ=0.15 ms时的计算延迟更低。
TwitterSentiment作业相对于WordCount的计算更复杂,在相同环境下达到的实际吞吐量较低,因此根据参数调整实验的分析结果,实验设置的期望吞吐量从20 000 tuple/s递增到70 000 tuple/s,参数θ的取值分别为0.15 ms和0.17 ms。
如图8所示,由于作业本身计算复杂度高,实验设置的期望吞吐量最高达70 000 tuple/s,但原系统的实际吞吐量在约59 000 tuple/s时达到瓶颈。经FNDD策略的优化将实际吞吐量平均提高到68 500 tuple/s,较原系统平均提高了16.12%,受资源总量和作业复杂度的限制,其优化效果不是非常明显,但已有效提高了实际吞吐量。
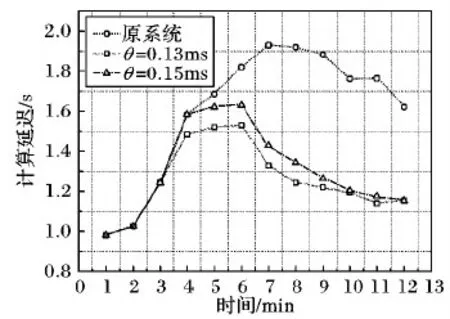
图7 WordCount延迟对比

图8 TwitterSentiment吞吐量对比
如图9所示,TwitterSentiment作业的计算延迟本身较高,其优化效果也相对明显:原系统在期望吞吐量上升时的延迟上升比较显著,通过算法优化将每1万条数据的计算延迟最多降低了416 ms,提高了计算的实时性;但两种参数取值下的延迟相差比较明显,当θ=0.17 ms时能够获得比较高的吞吐量,但其计算延迟也明显较高。
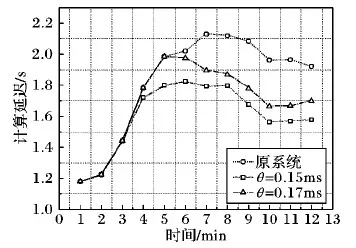
图9 TwitterSentiment延迟对比
TeraSort作业的计算复杂度和内存占用率最高,且计算过程中节点间有频繁的数据交互,根据参数调整实验的分析结果,将参数θ设为0.17 ms和0.19 ms,分别从吞吐量和内存占用率两个维度将FNDD策略与原系统的调度策略形成对比。
如图10所示,输入的最高期望吞吐量为50 000 tuple/s,而原系统能达到的最高实际吞吐量只有33 000 tuple/s,且计算延迟较高。通过FNDD策略的优化,集群的实际吞吐量最高可达到49 000 tuple/s,较原系统的实际吞吐量平均提高了38.29%,最大化利用了现有的计算资源且基本满足了期望吞吐量的要求,其中当θ=0.19 ms时的吞吐量能够稳步上升,集群的稳定性较高;但算法的优化是一个逐步提高吞吐量的过程,因此期望吞吐量达到40 000 tuple/s时保持稳定1 min,算法的执行过程有一定的时间开销,随着算法的执行集群的吞吐量进一步上升。
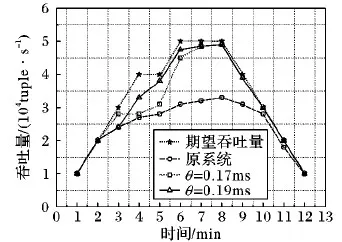
图10 TeraSort吞吐量对比
为了进一步验证FNDD策略对高复杂度作业的优化效果,实验在TeraSort作业执行过程中实时监控节点的内存占用率,通过定点采样得到如图11所示的实验结果:当期望吞吐量上升时,原系统将单位时间内新增的数据元组分配给一部分节点,导致其负载过高而内存占用率急剧上升,而另外一部分节点的资源未得到充分利用,导致部分节点无法及时处理数据而延迟加长。通过使用FNDD策略,使优化后集群被采样节点的内存占用率都有一定程度的上升且基本趋于稳定,每个有剩余资源的节点都分担了新增的计算负载,通过避免数据阻塞降低了计算延迟,实现节点间的负载均衡的同时稳步提高吞吐量。
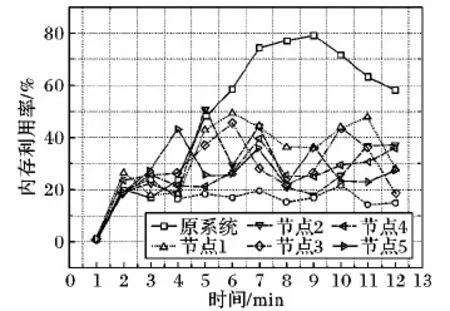
图11 TeraSort内存占用率对比
综上所述,实验表明FNDD策略在期望吞吐量上升阶段对集群的性能有一定的优化作用,通过检测每条边上容量与流量的差值,对新增的数据元组进行更合理的负载分配。在不同的作业类型下,该策略对原系统吞吐量的优化效果并不相同,但其平均优化比均高于16.12%。算法通过最大化利用集群的计算资源,在满足计算延迟约束的前提下有效提高了集群的实际吞吐量。
5 结语
由于数据源的多样性和输入速率的急剧变化给流式计算集群造成极大的负载压力,进而影响了计算的实时性和准确性,因此,本文提出基于流网络模型的动态调度策略,关注每个计算节点和传输链路的性能,在输入速率急剧上升时根据每条边上容量与流量的关系进行合理的负载分配,有效提高了集群的吞吐量;但FNDD策略关注集群输入速率急剧上升阶段的性能优化,这一阶段节点的计算和响应能力处于基本稳定状态,因此策略在作业开始时确定链路的容量大小。在任务执行的其他阶段,特别是在输入速率出现剧烈波动时,根据作业的执行情况动态调整容量的大小,能最大化利用集群的计算资源,因此,为了使FNDD策略能够适用于任务执行的各个阶段,下一步研究将重点关注容量的动态变化问题,根据作业执行情况和节点的剩余资源动态调整链路容量的大小,从而在任务执行的其他阶段取得更好的优化效果。

