组合型幂指函数三稳态随机共振微弱信号检测
张 刚,高俊鹏
(信号与信息处理重庆市重点实验室(重庆邮电大学),重庆 400065)
0 引言
微弱信号检测应用范围广泛涉及到光学、电磁学、数理学、物理力学、地质学、材料学等学科,因此微弱信号检测成为当前研究的热点[1]。微弱信号检测技术是用来检测噪声淹没下的有用信号,一般采用抑制噪声技术来提高信噪比(Signal-to-Noise Ratio, SNR),常规方法有时频分析[2]、经验模态分解法[3]、小波变换[4]等,这些方法在降噪的同时会使得有用信号受损。针对这个问题,本文采用随机共振方法,使噪声的能量向检测频率附近处发生转移,这种能量转移现象属于非线性系统中的一种动力学现象,因此构造不同的非线性系统模型,使得微弱信号的检测性能也不同。1981年Benzi等[5]首次提出“随机共振”(Stochastic Resonance, SR)的概念。目前随机共振理论已成为非线性科学领域的一个热点课题。随机共振现象是一种力学现象,它表征着驱动周期、噪声、系统参数三者能够达到协同效应[6],使得噪声的能量根据洛伦茨分布逐步向低频有用信号转移,从而提高系统输出信噪比,有效提高微弱信号检测性能。随机共振是根据线性响应理论和绝热近似理论[7],适用于低频(f≤1 Hz)的有用信号,但实际应用中,检测有用信号往往是大频率的,于是近几年学者提出了许多技术解决大频率这个问题,比如二次采样[8]、移频变尺度[9]、归一化尺度变换[10]等。以上方法都是从有用信号频率角度出发,然而在随机共振系统中,也可以从构造势函数的角度出发,不断提出一些新的势函数模型,如文献[11]提出了幂函数型单势阱随机共振的广义随机共振;文献[12]研究了Levy噪声下一阶线性系统的弱信号复原分析;同时文献[13]也提出Levy噪声激励下的幂函数型单稳态随机共振特性分析;文献[14]研究了基于幂函数型双稳态随机共振的故障信号检测方法。这些函数模型构造使得随机共振系统更加多样化,大大提高了随机共振检测能力,应用范围也比较广泛。
由于势函数模型多样化出现,随机共振效应仅驱动信号、噪声、系统参数三者达到协同作用从而实现更好的随机共振现象对应的输出信噪比,对参数优化有了一定要求,而不同势函数模型存在系统一个参数或多个参数,经过多年研究,有一些自适应参数寻优方法,比如果蝇算法[15]、人工鱼群算法[16]、遗传算法[17]、粒子群算法[18]等。在实际工业应用实践中,大型机械的轴承是工业生产中不可或缺的设备,通过随机共振微弱信号检测到轴承滚动的故障频率,能够减少工业生产中不必要的经济损失。为提高生产效率,学者们也做了大量研究工作,如文献[19]提出了级联双稳随机共振降噪下的经验模态分解,文献[20]基于多稳态随机共振系统提高输出信噪比实现轧机齿轮故障的诊断。
本文结合经典双稳态系统模型和高斯势阱(Gaussian Potential, GP)提出了一种新的组合型幂指函数三稳态随机共振模型。首先,通过对系统4个参数分析验证能够产生随机共振现象;其次,运用人工鱼群算法进行相应的参数寻优,检测多频信号;最后,通过工程实践,结合希尔伯特变换技术,验证了此方法具有更好的应用前景和实用价值。。
1 相关理论
1.1 双稳态系统下双势阱模型
双稳态系统中双势阱模型中,势函数Um(x)有一对对称的势阱,双稳态系统势函数表达式[14]如下:
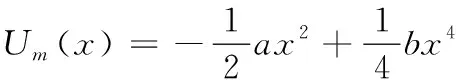
(1)
其中:a、b都是大于零的数,图1表示系统参数对于双势阱的影响。
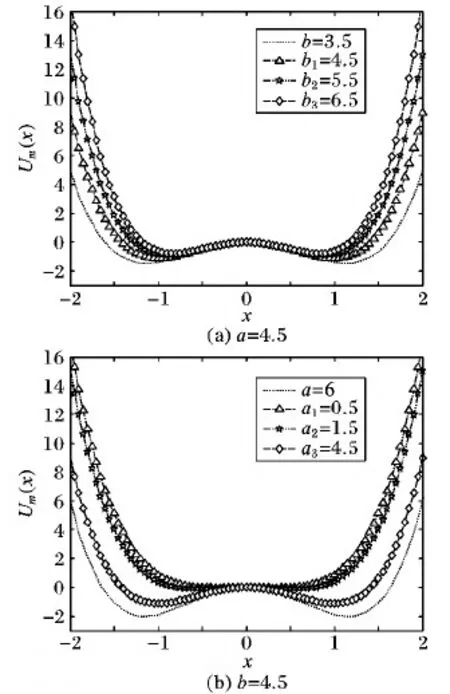
图1 双势阱势函数
图1(a)中固定数值a=4.5,当a值不变时,通过调节b的变化,可以得出一个结论:随b的数值增加势垒高度越来越小。图1(b)中固定数值b=4.5,当b值不变时,通过调节a的变化,可以看出:势阱高度变化随a值增加势垒高度越来越大,与图1(a)正好反相关。
1.2 GP势函数模型
被广泛应用于核物理学的GP势阱模型表达式[21]如下:
Ug(x)=-Vexp(-x2/R2)
(2)
其中:V表征势阱深度,R表征为势阱宽度。图2是GP单势阱图形,GP势函数的特别之处在于在单势阱两端都是收敛于零的势函数。图2(a)中固定V=3,可以看出随着R的增加,GP势阱壁逐步变得平缓;图2(b)中固定R=0.5,V从大到小变化时,GP势函数的势阱高度逐步变小。所以可以通过分别调节GP单势阱的系统参数V、R来改变势阱的高度和势阱壁的陡峭度的大小。
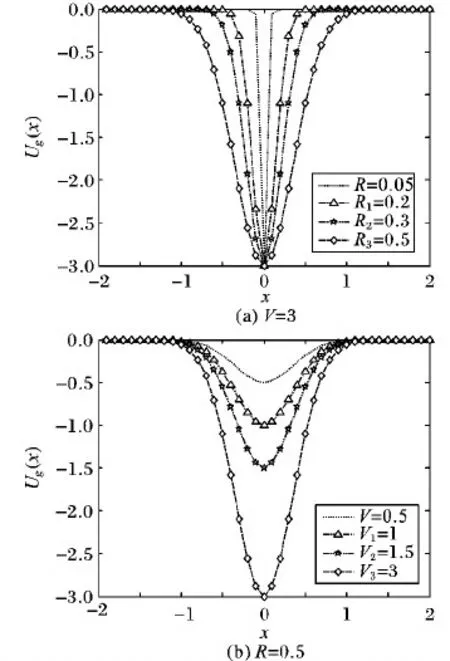
图2 GP单势阱势函数
1.3 幂指函数的组合模型
基于上述两种模型的一些特性,将双稳态势函数与Gaussian Potential单势阱势函数相结合,提出一种新型的幂指型三稳态势函数模型,势函数如下:
U(x)=Um(x)+Ug(x)=
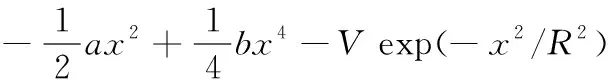
(3)
当系统参数a=6、b=4.5、V=2、R=0.3时构造出如图3所示的幂指型三稳态势函数。由图3可知,该函数有一对对称的势垒,可通过调节a、b、V、R使幂指型三稳态势函数的结构发生变化。由于加入GP势函数后,把原有的双稳态改变成了三稳态,使震荡粒子在双势阱变成三势阱跃迁,提高了噪声的利用率进而提高输出信噪比,从而达到更佳的随机共振现象。通过改变系统参数,可以在双势阱和三势阱之间进行转换,因此这个新型模型具备了双稳和三稳的一些特性。
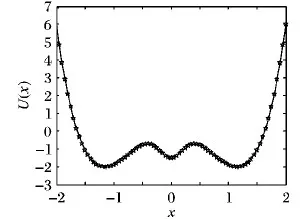
图3 组合型幂指函数三稳势函数
2 组合型随机共振系统
2.1 共振系统方程
用朗之万方程来描述粒子运动的数学模型,方程如下:
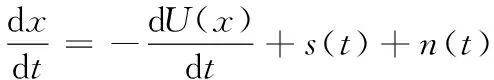
(4)
其中:s(t)是驱动周期;n(t)是期望为零、方差为2Dδ(π)高斯白噪声,其中δ(π)期望为0、方差为1,D是噪声强度。通过把式(3)代入式(4)中得到式(5):
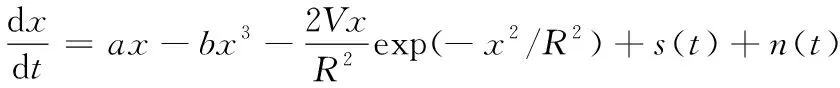
(5)
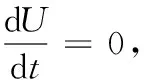
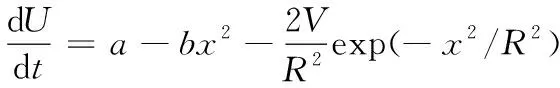
(6)
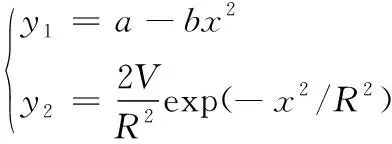
(7)
势函数的解的个数符合一般三稳态的势函数,需要数值仿真来验证式(4)、(5)能出现随机共振现象。
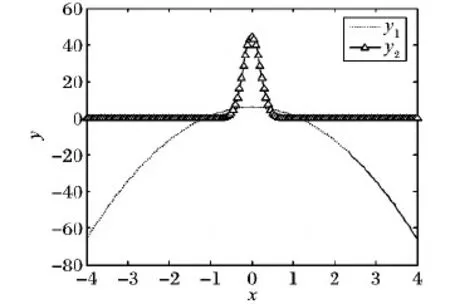
图4 方程组解的个数
2.2 参数优化对系统影响
目前随机共振的测量指标有许多种,例如相关系数、特征频率峰值、功率谱放大系数、信噪比增益、平均输出信噪比等,本文主要采用的是平均输出信噪比。信噪比定义如下:
SNR=10 lg(S/N)
(8)
其中:S是原始驱动周期信号,N是噪声信号 。平均输出信噪比定义为:
(9)
其中n表示仿真系数。
首先考虑噪声强度D对平均输出信噪比的影响。通过调节其他参数取a=1.5,b=3.5,V=3.7,R=2.5,D以在0.01~5以0.05为步长取值。经过100次实验取平均,可得到图5。可以看出,随着噪声强度增加导致平均输出信噪比先增加后减少,在某一个噪声强度时达到最大输出信噪比。因此,组合型幂指三稳随机共振具有随机共振的现象。
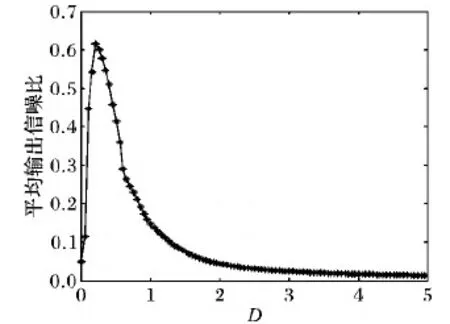
图5 组合型幂指函数三稳态随机共振系统的平均输出信噪比随着参数D的变化
图6为四个系统参数和系统输出的平均输出信噪比之间的函数关系,它们共同的现象是存在一个单峰值曲线,规律都是先增加后减少的趋势,可以看出构造组合方程与系统参数具有非线性关系。图6表明系统参数对系统输出的能量分布起着十分重要的作用,因此调节系统参数能使组合系统产生随机共振现象。上述分析表明,在组合型共振系统模型中,通过调节四个系统参数使得SR系统中信号和噪声的能量分布发生变化,可以实现噪声能量向信号能量转移,从而达到用噪声增强有用信号的效果。
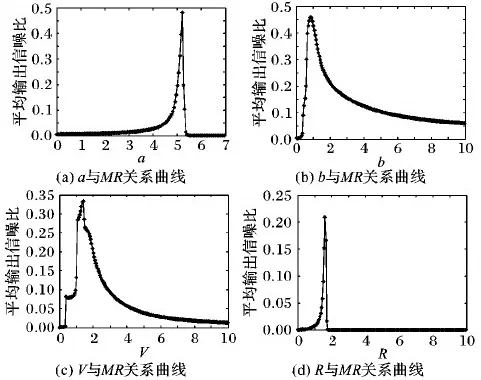
图6 系统参数与系统输出SNR的关系
如图6所示,调节系统参数,能够使得系统达到随机共振现象,而单独对每个参数分别优化,使系统达到随机共振现象,会忽略参数之间相互作用,人工鱼群算法可以对所有系统参数进行并行优化,克服参数相互作用的缺点,该算法鲁棒性强,对初始值不明感,易于设置初始值的范围。该算法的主要行为有:觅食行为、聚群行为、追尾行为和随机行为。设置人工鱼群算法的参数,包括鱼群个体的数量N,鱼群的活动范围LBUB(Low Bound Up Bond),鱼的感知范围Visual。鱼的最大移动步长step,尝试次数try_number, 最大迭代Maxgen,拥堵因子δ,di, j表征人工鱼个体之间的距离。将目标函数定义为Y=f(x)=SNR。算法实现步骤如下:
步骤1 初始化N=20条人工鱼,感知范围Visual为[0,20],移动步长step=0.1,拥挤因子δ=0.618,尝试次数try_number=50,当前迭代次数gen=0,最大迭代次数Maxgen=100,当前觅食行为次数n。
步骤2 计算并筛选鱼群所有个体当前状态最优的目标函数作为当前公告板上的初始化值。
步骤3 执行聚群行为。设人工鱼群当前状态为Xi,在当前邻域内(di,j
步骤4 执行追尾行为。设人工鱼群当前状态为Xi,在当前邻域内(di,j
步骤5 执行觅食行为。设人工鱼当前状态Xi,在感知范围内随机选取下一刻状态的人工鱼Xj,代入目标函数计算出Yj,如果Yj>Yi,向该方向移动一步;如果不满足,且在需要尝试次数try_number后仍然不满足时,则更新公告板。
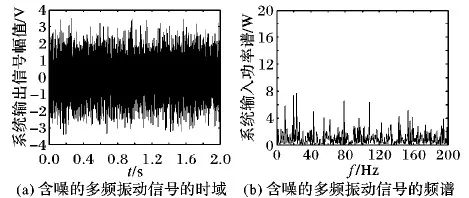
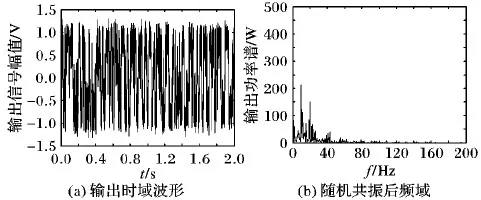
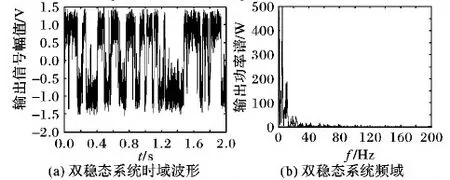
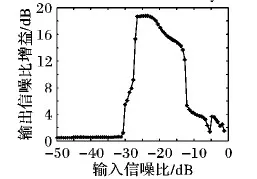
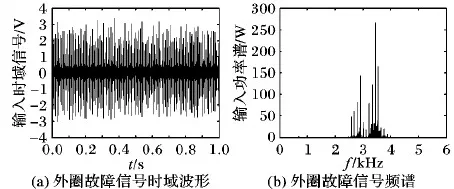
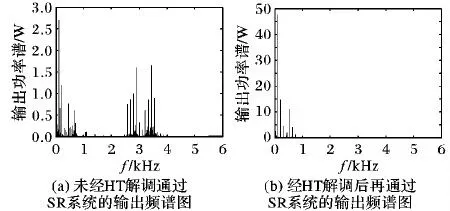
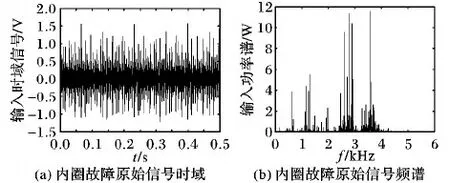
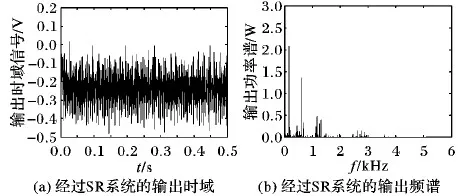
步骤6 若gen 步骤7 输出公告板上的最优解,并记录最优的目标函数相应的4个最优参数值。 本文采用二倍频的周期信号来验证构造的幂指型周期函数能够产生随机共振并且比经典双稳态系统的性能更优。这种构造多频含噪的周期信号为: s(t)=A1·sin(2π×ft)+A2·sin(2π×2ft) (10) 其中:周期信号频率f为10 Hz,周期信号的幅值为A1=A2=0.04,外加入噪声强度为0.8的高斯白噪声,由于采用的是大频率的信号,所以依据二次采样定律对大频率进行预处理,采样频率fs=5 Hz, 二次采样频率fsr=5 000 Hz,采样点数为10 000。预处理后信号分别通过幂指组合型三稳态系统和双稳态随机系统,双稳态系统的参数常规设置(a,b)=(1,1),而幂指组合型三稳态系统经过人工鱼群寻优的参数为(a,b,V,R)=(5.575,2.889,4.643,1.323)。图7(a)是含噪的信号时域波形图,图7(b)是含噪的频域图,而在频域图中特征频率处不能够明显辨别出该频率处的峰值,在10 Hz、20 Hz处峰值分别是5.835 W、7.4 W。原始微弱信号采用信噪比是-25.8 dB。通过二次采样后,通过幂指型随机共振后,如图8所示,在频域图中特征频率10 Hz,20 Hz处,分别为213.1 W、150.4 W。组合三稳系统输出信噪比为-8.59 dB。如图9,在频域图中特征频率10 Hz,20 Hz点处,分别为178.4 W、30.64 W,双稳系统输出信噪比为-13.1 dB。说明在噪声强度为0.81时,通过参数调节,组合三稳系统与双稳系统相比,组合三稳系统的输出信噪比提高了一倍多。系统性能通过信噪比增益来表征,如图10所示。增加不同的输出信噪比,系统性能信噪比在-30 dB附近是个拐点,信噪比大于-30 dB时,开始出现随机共振现象。 图7 原始的含噪多频振动信号 图8 组合型幂指函数三稳态随机共振 图9 双稳态系统时域与频域波形 图10 幂指组合型三稳态系统输入信噪比对系统输出的影响 滚动轴承故障信号是具有调制性、非平稳性的微弱信号,常常被强大的机械噪声淹没,利用本文新型系统模型的检测系统对机械滚动轴承进行故障诊断,能够检测故障频率,因此新型检测系统具有良好的检测性能。该实验平台采用Case Western Reserve University Bearing Data center[22],选用的对象是6205-2RS JEM SKF的深沟球轴承,分别对外圈和内圈故障进行检测。外圈故障的特征频率为107.3 Hz,内圈故障的特征频率为162.2 Hz;轴承转速为r=1 796 r/min,采样频率为12 000 Hz,二次采样频率为5 Hz;外圈采样点为12 000。 图11是外圈原始信号时频图,通过智能算法寻优得到一组参数(a,b,V,R)=(3.141,3.962,5.228,1.915)和图12,其中图12(a)是经过未解调直接通过SR系统中输出频谱图;图(b)是经过解调预处理后,再通过SR系统中输出频谱图。可以看出,通过解调后可以把原先高频处的频谱去掉,比较好地检测出二倍频。针对内圈故障检测,所取采样点为6 000,一组寻优参数为(a,b,V,R)=(2.557,3.752,2.343,1.336)。图13是原始内圈故障的时域和频域图,经过智能算法寻优的参数调节后,得到如图14所示检测出的时域和频谱图,在162 Hz处功率谱为2.073 W,与检测前的输入功率谱相比,输出频谱功率提高了5倍。因此组合型三稳随机共振系统应用于故障诊断中具有一定的检测效果。 图11 外圈故障信号 图12 外圈故障频谱对比 图13 内圈故障信号 图14 内圈经过SR系统输出信号 本文把经典双稳势函数和Gaussian Potential单势阱势函数组合成一种新型的幂指型的三稳势函数,形成了新型的幂指型组合型三稳随机共振系统。通过高斯白噪声强度与系统输出平均信噪比的变化规律,来验证该幂指组合型系统能够产生随机共振现象;再通过人工鱼群算法进行四个参数的寻优,找到能使得系统输出最佳的平均信噪比;通过最佳四个参数检测大频率的谐波信号,对比双稳系统,仿真结果显示,新型的三稳系统通过对噪声的利用率高于双稳系统,即输出平均信噪比高于双稳系统;最后把新型的系统应用于故障诊断中对内外圈的故障进行诊断,对于内外圈故障检测,经过随机共振系统能检测出故障频率,使得高频分量被滤除掉,进而达到了最佳的检测效果。3 系统仿真与应用
3.1 双频振动周期信号检测
3.2 工程应用
4 结语

