基于扩张状态观测器和反步滑模法的四旋翼无人机轨迹跟踪控制

张建扬，于春梅,2，叶剑晓

(1.西南科技大学 信息工程学院，四川 绵阳 621000； 2.特殊环境机器人技术四川省重点实验室(西南科技大学)，四川 绵阳 621000)

0 引言

近年来，由于四旋翼无人机(quadrotor Unmanned Aerial Vehicle, quadrotor UAV)具有结构相对简单、生产成本较低等优点，在军事和民用领域备受青睐[1]。轨迹跟踪控制是无人机完成特定任务的基础，因此，提高无人机的轨迹跟踪精度和性能具有重要意义。

四旋翼无人机是一个4输入、6输出的欠驱动系统[2]，系统变量间存在半耦合关系且模型中存在非完整性约束,这增加了控制器设计的复杂度。在实际飞行中，由于无法对空气动力建立精确的数学模型且模型中的无人机质量、转动惯量、空气动力学系数等参量的测量值与实际值之间存在偏差,同时桨叶转动、急风、地磁影响等外界未知干扰也会对其产生较大的影响[3-4]，从而进一步增加了四旋翼无人机的控制难度。因此，设计出能够克服系统内部扰动和外部噪声的无人机控制系统是轨迹跟踪的重中之重，即整个系统必须具有鲁棒性。

为了克服上述困难，国内外专家学者进行了大量的研究，已经有较多的解决方案被提出。如文献[5-7]研究了四旋翼无人机的反步法控制，由于反步法对精确的数学模型有较高要求，因此建模误差的大小会对系统的跟踪效果产生影响；文献[8]基于四元数法建立了无人机的数学模型，内、外环分别采用H∞控制和积分型反步法控制，较好地补偿了系统的内外干扰；文献[9-10]研究了滑模控制，虽然滑模变结构对系统参数变化不敏感，抗干扰能力较强，但当系统存在较强复合干扰时，无人机的控制精度并不理想；文献[11]将反步法和滑模控制相结合，能够较好地完成跟踪任务；文献[12]采用不需要模型的神经网络方法来估计系统的内扰和外扰，取得了良好的跟踪效果，但神经网络控制要求有足够多的基函数来保证逼近精度，这严重增加了计算负担；文献[13]采用扩张状态观测器(Extended State Observer, ESO)方法在线估计系统的不确定性因素，取得了良好的控制效果，但姿态角幅值变化较大。

考虑各种方法的优缺点，本文在文献[11]的基础上设计了一种基于ESO和积分反步滑模算法的鲁棒控制器，将抗干扰能力较强的滑模控制融入到反步法控制器中，使系统的鲁棒性得到增强；接着引入积分环节以减小系统的稳态误差；最后，为了抑制内、外干扰，利用ESO来估算系统的总扰动量并在控制量中进行补偿。通过Lyapunov稳定性分析验证了控制器的有效性，并结合仿真分析验证了该算法的跟踪性能。

1 四旋翼数学模型

四旋翼无人机的空间运动分为质心运动和绕质心运动两个部分，因此首先要建立如图1所示的两个坐标系：机体坐标系Oxyz和地面坐标系Oexeyeze。

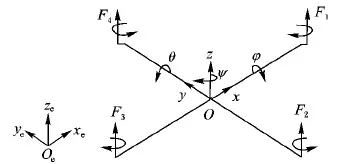
图1 四旋翼无人机坐标系

假设四旋翼无人机为结构对称、质量分布均匀、质心与机体坐标系原点一致的刚体，并忽略空气阻力和低雷诺数的影响，再考虑外界干扰n(t)和系统未建模Δf(t)，两者的总和记作σ，基于文献[14]的数学模型，并且为了便于反步法的研究，可得严反馈形式下的四旋翼无人机模型:

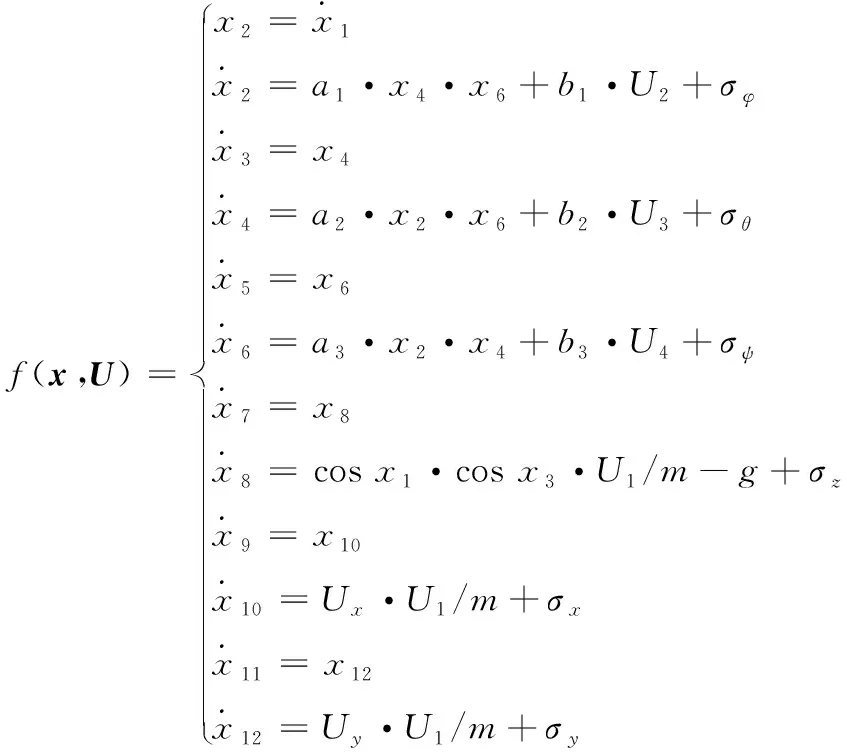
(1)

式中，状态变量

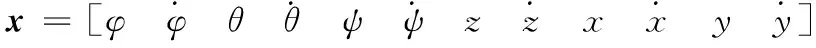
即：

a1=(Jy-Jz)/Jx，a2=(Jz-Jx)/Jy，

a3=(Jx-Jy)/Jz，b1=l/Jx，

b2=l/Jy，b3=1/Jz

U2=F4-F2=b(ω42-ω22)

U3=F3-F1=b(ω32-ω12)

U4=k(ω22+ω42-ω12-ω32)

Ux=cosφsinθcosψ+sinφsinψ

Uy=cosφsinθsinψ-sinφcosψ

其中：m为四旋翼无人机的质量；x、y、z为地面坐标系下的位置信息，φ、θ、ψ为地面坐标系下滚转角、俯仰角、偏航角；l为旋翼中心到机体坐标原点的距离；Ji(i=x,y,z)为转动惯量；U1～U4和Ux、Uy为控制输入；ωi(i=1,2,3,4)为四个电机转速；b为升力系数；k为阻力系数。

2 基于ESO的复合干扰估计

ESO的作用是在仅知道系统输入和输出的情况下实现对各个状态变量和系统总扰动量的估计，然后在控制律中实时补偿，从而达到克服系统内部扰动和外部噪声的目的。鉴于观测器所估算的扰动是内扰与外扰的和[15],不仅系统的抗干扰能力得到提高，同时也让建模误差对跟踪效果的影响降到最低。

为了方便ESO的设计，将数学模型式(1)改写为：

(2)

其中：

ξ1=[x1x3x5x7x9x11]T；

ξ2=[x2x4x6x8x10x12]T；

g(t)=[a1x4x6+σφa2x2x6+σθa3x2x4+σψ-g+σzσxσy]T，它为6通道各种扰动的和(包括未建模、建模动态和外部扰动)，且其导数有界；U=[U2U3U4U1UxUy]T。

设计如式(3)所示的扩张状态观测器：

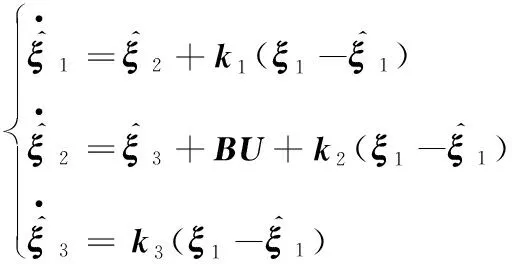
(3)

通过以上扩张状态观测器，可估算出6通道的总干扰g(t)，然后在控制律中实时补偿，增强系统的鲁棒性。

3 积分型反步滑模控制器设计

3.1 控制结构设计

由数学模型可知，四旋翼无人机控制量U2、U3、U4的大小影响姿态角的变化，而姿态角与控制量U1又共同决定位置信息的变化，即当已知U2、U3、U4这3个控制量时，3个姿态角及角速度信息就能被解算出来，如果当U1已知，无人机的位置和速度信息也能推算出来。很显然它们之间存在半耦合关系，因此，采用双闭环结构，即姿态内环、位置外环。期望姿态和期望位置：ξ1d=[x1d,x3d,x5d,x7d,x9d,x11d]T=[φd,θd,ψd,zd,xd,yd]T，其控制结构如图2所示。

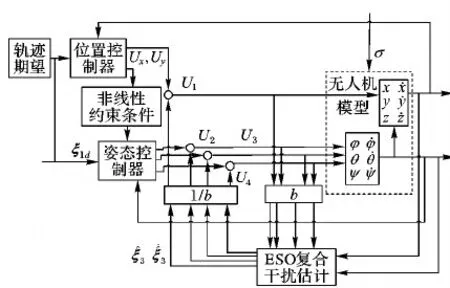
图2 基于ESO的四旋翼无人机控制结构

3.2 控制器设计

仍以数学模型式(2)为对象设计控制器，步骤如下。

定义误差变量z1=ξ1d-ξ1，并对误差变量求导：

(4)

引入一阶跟踪误差的积分：

(5)

引入虚拟控制量α，定义误差变量:

z2=ξ2-α

(6)

取Lyapunov函数：

其中n为正常数对角矩阵。

对V1求导得：

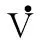
(7)

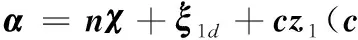
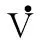
(8)

由式(7)、(8)推出：

(9)

(10)

取Lyapunov函数：

求导得：

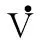
(11)

取滑模面S=z2，代入得：

(12)

即

(13)

规定指数趋近律：

(14)

其中，ε1、ks为正常数对角矩阵。

(15)

至此，就完成了6通道控制量U的设计。

稳定性证明如下：

将式(8)、(14)代入式(11)得:

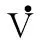
(16)

当S→0时，STS<0，能够满足滑模面存在及可达的必要条件，即z2→0时：

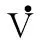
(-cz1)Tz1< 0

(17)

由Lyapunov稳定定理可知，系统渐进稳定。

3.3 非线性约束条件

由上述数学模型可知，四旋翼无人机的实际输入是四个电机的升力F1、F2、F3、F4，而输出则为φ、θ、ψ、x、y、z六个状态，因此，四旋翼无人机具有欠驱动性特性，其必须通过姿态角来间接控制无人机的水平运动。因此，在双闭环控制器设计中，通过反解水平控制量Ux、Uy来获得滚转角和俯仰角的期望值x1d、x3d，即所谓的非线性约束条件。

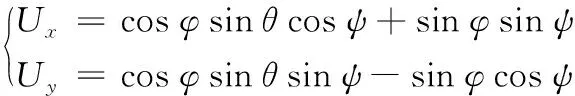
(18)

通过反解式(18)可以得出要实现控制量Ux、Uy所需的期望姿态角指令：

(19)

4 系统仿真分析

为验证所提控制算法的有效性，采用螺旋上升法对其仿真验证。设置期望轨迹为：

期望偏航角ψd=0。

四旋翼无人机各参数如下：m=1.4 kg，g=9.81 m/s2，Jx=0.03 kg·m2，Jy=0.03 kg·m2，Jz=0.04 kg·m2，l=0.2 m，k=4.003×10-7N·m·s-2，b=1.923 21×10-5N·s2。

仿真实验中，各参数选择如下：k1=diag(120,120,120)，k2=diag(4 400,4 400,4 400)，k3=diag(48 000,48 000,48 000)，ε1=diag(25,25,25,2.5,2.5,2.5)，ks=diag(50,50,50,6,6,6)，n=diag(3,3,3,3,3,3)，c=diag(50,50,50,30,30,30)。

无人机初始位置[xyz]T=[0 0 0]T，初始姿态角[φθψ]T=[0 0 0]T，初始角速率[pqr]T=[0 0 0]T。位置环施加的复合干扰均为2 sint，姿态环施加的复合干扰为[sin 2t0 sin 2t]T。仿真结果如图3～7所示。

结果分析：1)从仿真图3、4可以看出，在施加复合干扰的情况下，采用ESO和积分型反步滑模算法设计的控制器，跟踪误差最大仅有0.06 m，跟踪效果显著，有较强的抗干扰能力，基本满足无人机的跟踪要求；而采用反步滑模控制时，跟踪误差最大为0.25 m，抗干扰能力较差。2)从仿真图5、6可以看出，两种算法在姿态角上都有良好的跟踪效果，但采用ESO对复合干扰进行估计并补偿时，得到的姿态角振幅仅有0.05 rad，并且振荡频率较低，仅为0.1 Hz，飞行较为稳定；而采用反步滑模控制算法时，振幅最大为0.5 rad，并且姿态角变化剧烈，频率为0.4 Hz，飞行不稳定。3)从仿真图7可以看出，ESO能够精确地对复合干扰进行估计，减小了复合干扰对系统跟踪精度的影响，从而增强了系统的抗干扰能力。

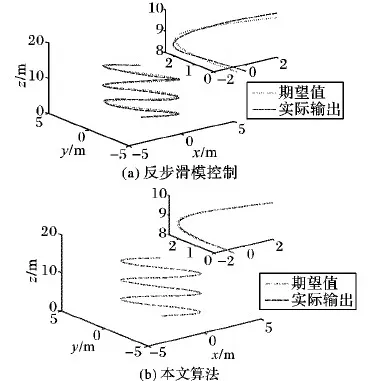
图3 轨迹跟踪三维效果对比

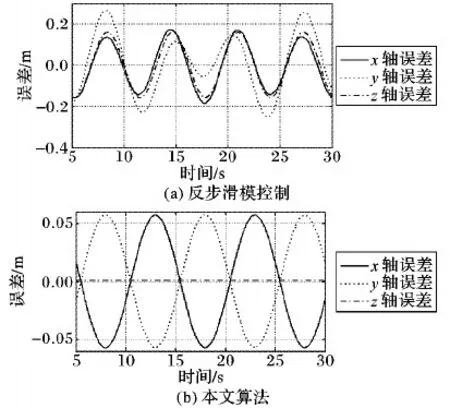
图4 轨迹跟踪误差对比

图5 反步滑模控制的姿态跟踪效果

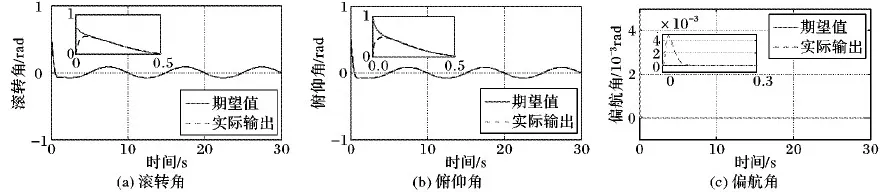
图6 本文算法的姿态跟踪效果

图7 ESO复合干扰估计

5 结语

本文针对欠驱动四旋翼无人机，从实际应用角度出发，考虑存在外界干扰和系统参数摄动的情况，设计了一种基于ESO和积分型反步滑模算法的鲁棒控制器。通过该方案，只需要得知系统的输入和输出，就能够精确估算出系统所受内、外总扰动的值，然后在控制律中实时补偿。通过对比仿真实验可以看出，在系统受到干扰时，该算法能够使系统的抗干扰能力增强、跟踪精度更高，并且姿态角变化频率低，波动幅值较小，飞行更加稳定。