基于动态时间规整的空中目标机动识别*
姚佩阳,周旺旺,张杰勇,王 勋
(空军工程大学信息与导航学院,西安 710077)
0 引言
对空中目标的机动识别是判定其战术意图的重要依据,因为空中目标的战术意图总是要通过一定的机动动作来实现[1]。当前,许多意图识别算法中都将空中目标的机动识别结果作为其意图推理的变量考量[2-3]。若能及时准确地判断敌方空中目标采取的机动动作,有利于我方掌握其作战意图,采取有针对性的应对策略,进而占据空战优势,掌握主动权。
文献[4]提出基于知识的飞行动作快速识别方法,采用产生式规则建立飞行动作识别知识库,实现对飞行动作的识别。文献[5]提出基于遗传算法的飞行动作识别方法,用于建立飞行动作识别专家知识库。文献[6-7]提出利用目标跟踪得到的运动参数结合HMM对目标进行机动识别。文献[4]算法是建立在目标运动参数已知的情况下,然而现实条件下,受传感器精度和自然条件因素的影响难以获得如此精确、全面的运动参数。文献[5]算法主要用于飞行动作识别专家知识库的建立,对具体机动识别过程没有进行深入研究。文献[6-7]均利用目标跟踪得到的运动参数结合HMM对目标进行机动识别[8],而HMM算法在训练阶段要提供大量的训练样本[9],通过反复计算才能得到参数模型,计算量较大,耗时较长。HMM的识别效果依赖于训练的样本,参加训练的样本越多,识别效果越好,事实上,大量的敌方目标的飞行数据是难以获得的,实际的问题更多是在低训练样本下如何获得较高的识别率[10]。
为克服空中目标飞行数据获取困难、识别率不高和实时性较差的问题,本文提出了一种基于动态时间规整的空中目标机动识别方法。通过对目标跟踪产生的空中目标飞行轨迹进行机动序列提取作为测试模板,运用DTW算法将测试模板与参考模板进行匹配,识别空中目标的机动类型。实验结果表明,在低训练样本条件下,DTW算法较HMM算法识别率高,识别时间短。
1 空中目标机动类型及其序列表示
1.1 空中目标的机动类型
空中目标的机动类型复杂多变,但始终是围绕其作战任务进行的,体现了其作战意图。因此,可以结合领域专家知识和以往作战训练的经验,对空中目标的机动进行识别。图1列举了几种典型的空中目标机动类型。
1.2 空中目标机动类型的序列表示
空中目标飞行轨迹是一条连续的运动曲线,为了对空中目标进行战术机动识别,必须对目标飞行轨迹进行分割分类识别。轨迹分割分类识别是为了在提取空中目标飞行轨迹中的主要战术机动动作,并产生相应的机动序列。通过对空中目标飞行轨迹的不间断处理,得到一个与其战术机动动作相对应的机动序列,这样,空中目标的战术机动就可以用一个离散的序列来表示。
定义1 除进行空战格斗与起降外,空中目标一般不进行纵向运动。因此,若将空中目标的机动限定在水平剖面上,那么空中目标的运动状态为:直飞、向左转和向右转。
定义2 为了突出左转与右转的区别,使用1代表左转,2代表直飞,3代表右,使得序列欧式距离(欧几里得距离)增大,进一步提升机动区分度。
定义3 空中目标的机动类型用离散时间序列A1,A2,A3,…,Ai,1≤i≤10 表示。
利用领域专家知识和以往作战训练的经验对典型的空中目标机动类型进行序列提取,得到如表1所示的空中目标机动类型的典型序列。
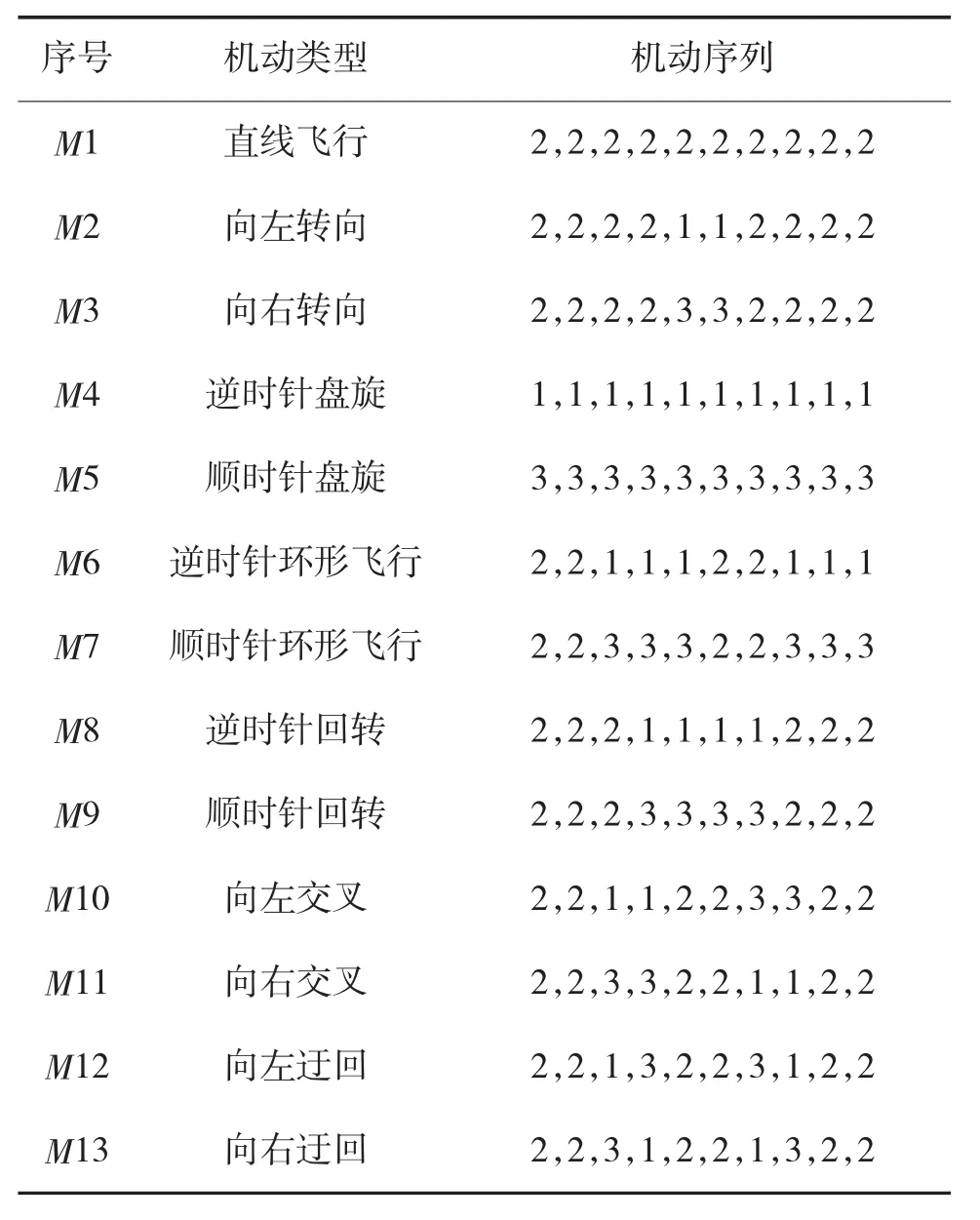
表1 空中目标机动类型的典型序列
2 识别算法实现
2.1 机动序列提取
空中目标飞行轨迹的机动序列提取是后期进行机动识别的基础,关系到后期识别的准确率。本文提出,将目标跟踪得到的空中目标轨迹进行滤波处理,得到空中目标的运动曲线,每一个时间点就是机动序列的取样点。
空中目标的机动序列值可由下式描述:
式中L为点3与点4纵坐标差值。点4是空中目标飞行轨迹上连续两个点,点1、点2的延长线上与点3横坐标相同的点。δ为判断是否转弯设定的阈值,取值为0.5。i是提取机动的序列号。
具体的序列提取方法如下:序列提取需要用到连续的3个量测点,将点1、点2的连线延长,测量其与X轴、Y轴正向的夹角,并在连线上取与点3横坐标相同的点4,将点3与点4纵坐标差值记为L。以点1、点2连线与X轴夹角α、与Y轴夹角β为锐角为例,L值大于设定的阈值δ,表示在点3进行了左转,用特征值1表示;L值在阈值范围内(-δ≤L≤δ)时,表示在点3保持直线飞行,用特征值2表示;L值小于设定的阈值-δ,表示在点3进行了右转,用特征值3表示。如图2所示,图2提取的序列为[2 2 2 2 1 1 2 2 2 2]。
2.2 基于DTW的机动识别
2.2.1 模板匹配基本原理
模板匹配法是模式识别中常用的一种匹配方法,广泛应用在图像、语音等识别领域[11],但在空中目标机动识别中模板匹配运用较少。模板匹配是对每一个类别建立一个或多个参考模板,文中通过将典型的空中目标机动类型转化为不同的模板,建立了一个基于模板匹配的简单空中目标机动识别系统。
参考模板用R=[r1,r2,r3,…,rm,…,rM]表示,m为参考模板的时序标号,M为参考模板所包含的序列总数,rm是第m个序列的特征值。
将要识别的机动序列称为测试模板,用T=[t1,t2,t3,…,tn,…,tN],n 为测试模板的时序标号,N 为测试模板所包含的序列总数,tn是第n个序列的特征值[12]。
2.2.2 动态时间规整
动态时间规整(DTW)是通过计算T与R之间的累积最小欧式距离。当n=m时,可以通过直接计算T和R的距离,距离越小,两个序列相似度越高。当n不等于m时,DTW采用动态规划(Dynamic Programming,DP)[13]方法来识别。
为了对齐两个不等长序列,需要构造一个n*m的矩阵,每一个矩阵元素(i,j)表示点 ti与 rj对齐,DP算法可以归纳为寻找一条通过此网格中若干点的路径,用W表示。
W 上的第 k 个元素定义为 wk=(i,j)k,路径 W 通过的格点即两个序列对齐的点。路径的选择满足以下3个约束:
1)边界条件:提取的空中目标机动序列的先后次序不能改变,因此,选择的路径一定是从左下角出发,到右上角结束。即 w1=(1,1),wk=(m,n)。
2)连续性:匹配过程中只能和自己相邻的点对齐,以确保R和T中的每个坐标都出现在W中。即若wk-1=(a′,b′),则wk=(a,b),(a-a′)≤1,(b-b′)≤1。
3)单调性:W上面的点须随着时间单调前进,不能折返。即若wk-1=(a′,b′),则wk=(a,b),(a-a′)≥0,(b-b′)≥0。
结合路径选择的3个约束条件,每一个格点的路径就只有3个方向。既如果路径已经通过格点(i,j),则下一个格点只可能是 (i+1,j),(i,j+1) 或是(i+1,j+1)。满足3个约束条件的路径是指数级的,而目标路径是规整代价最小的路径:
式(3)中分母K用来对不同长度的规整路径的补偿。
为计算T与R之间的累积欧式距离,定义ti和rj两点之间的距离为d(i,j),T到R的累积欧式距离 D(n,m)。累积距离 D(n,m)为当前格点欧式 ti和rj之间欧式距离与最小可达邻近元素的累积距离之和:
式(4)中,当 i=1 时,D(i-1,j-1),D(i-1,j)为无穷大;当 j=1 时,D(i-1,j-1),D(i,j-1)为无穷大;当 i,j=1时 D(i,j)=d(1,1)。累积距离 D(n,m)最小的序列即为相似度最高的序列。
2.2.3 DTW的机动识别
基于DTW的机动识别流程步骤如下:
步骤1 输入传感器得到的待识别空中目标飞行轨迹;
步骤2 按式(1)提取待识别的空中目标飞行轨迹观测序列;
步骤3 按式(4)计算测试模板与参考模板T的路径积累距离 D(n,m);
步骤4 重复步骤3,直到测试模板T与所有参考模板R匹配,得到最小累积距离Dmin(m,n)的参考模板即为识别结果。
3 实验仿真
基于领域专家知识和以往作战训练的经验对13种机动类型生成147个训练样本,测试库由实际飞行轨迹获得。分别用HMM算法和DTW算法对测试库中的飞行轨迹进行识别,得到实验结果。图4为使用HMM算法对图2中给定飞行轨迹识别的结果,图5为使用DTW算法对图2中给定飞行轨迹识别的结果。
通过设定判别函数阈值,排除明显不符合识别要求的机动序列,使两种算法均在拒识率为5%条件下,比较识别率。识别结果如表2所示。DTW算法的识别率为93.64%,高于HMM算法的89.98%,且识别时间较短。因此,DTW算法在识别效果上优于HMM算法。
HMM算法是一种统计方法,在训练阶段需要大量的训练样本,事实上,空中目标的飞行数据是不易获得的,也因此导致HMM算法在机动识别中误识率较高。现实面临的问题更多是在低训练样本情况下,尽可能提高识别率。DTW算法是基于动态规划方法进行识别,因此,在训练样本较少的情况下,就能有效地对空中目标进行机动识别[14-15]。
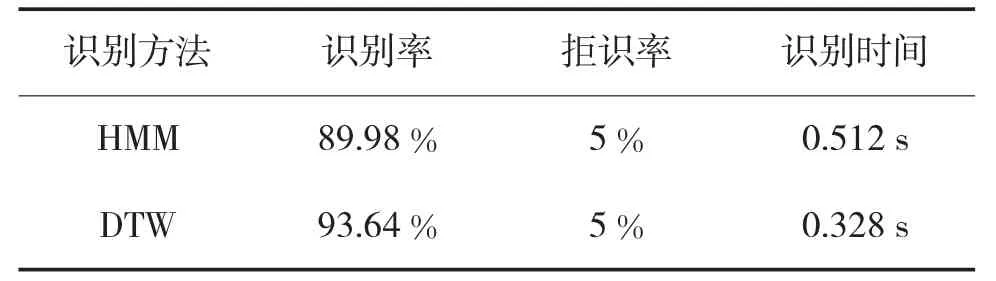
表2 HMM和DTW算法的识别结果
4 结论
空中目标的机动识别是判定敌方作战意图的重要依据,快速、准确地对识别空中目标的机动类型有利于我方掌握战场主动权。本文将从空中目标飞行轨迹提取出的机动序列作为机动识别的测试模板,运用动态时间规整算法将测试模板与参考模板进行匹配,识别空中目标的机动类型,实现了目标跟踪与机动识别的有机结合。与HMM算法比较,DTW算法在低训练样本条件下识别效果更好。

