基于Adam神经网络的顾客满意度预测与应用

张 枫，杜阳宇，张庆磊

(武汉理工大学 机电工程学院,湖北 武汉 430070)

随着企业所处的外部环境的变化，企业对于顾客满意度的要求有了新的内涵，企业不仅需要让顾客买到质量好的产品，还需要在交易过程中提供良好而满意的服务，从而让顾客得到心理上的满足。建材装备制造企业为了提高市场占有率和获得更高的收益，必须提高顾客满意度并且控制质量成本。因此，如何让企业以最小的质量成本提供最优质的服务，赢得更多客户的认同，对于建材装备制造企业来说是一个严峻的挑战。

对于质量成本和顾客满意度国内外学者进行了大量的研究。尚姗姗等[1]通过建立系统动力学仿真模型来研究不同质量水平下质量成本各组成部分间的关系，并通过灰色线性回归组合模型建立质量成本与质量水平间的关系模型。罗卉等[2]根据投入产出理论和数据包络分析方法，提出了对质量成本管理体系进行综合评价的模型，并以实例验证了该模型的合理性。李成翔等[3]基于六西格玛理论分析不同质量水平对配电网开关柜质量成本的影响程度，为供电企业在采购配电网开关柜时提供参考意见。Tim等[4]采用参数化的距离函数方法，辩识生产技术、潜在质量费用和其他投入成本之间的关系。最后证明边际质量成本的改善可以带来巨大的质量提高。Krystel等[5]指出质量成本曲线模型应该结合内外部因素研究，而不仅限于内部成本研究，为质量成本研究领域的延伸做出了贡献。Al-Tmeemy等[6]对空调装备公司进行调查，在使用索引技术的基础上对企业质量成本控制的结果加以检验和分析，构建了企业质量成本控制管理系统。杨瑞[7]在对比分析传统质量成本模型和基于顾客满意的质量成本模型的基础上，提出了企业开展持续质量改进活动可采取的措施。郑蓓蓉等[8]分析了顾客满意度与企业质量成本之间的关系，并通过实证分析，提出了企业在降低质量成本的同时提升顾客满意度可以采取的方法和策略。肖静[9]重新思考顾客满意视角下质量成本管理的涵义并构建基于顾客满意的质量成本体系以及以顾客满意为导向的质量成本系统动力学模型。潘燕华等[10]将顾客满意度与质量成本的关系用一张“地图”直观地演绎出来。苏笑笑[11]将由于顾客满意度下降造成的隐形成本损失加入到质量成本的构成要素，提出了基于顾客满意度的隐性损失成本的核算公式，并在此基础上对隐性损失成本控制进行分析。张晓冰[12]以质量为中介对顾客满意与质量成本控制的关系进行联结，构建了包含“基于价值工程的目标质量成本预测法—前馈控制、作业成本法—过程控制、质量成本信息报告—反馈控制”的基于顾客满意的质量成本集成控制模型。

笔者在以上学者的研究基础上，针对建材装备制造企业建立顾客满意度预测模型，运用基于Adam神经网络对顾客满意度进行预测，利用Adam算法对神经网络进行优化，弥补神经网络收敛速度慢、容易陷于局部最优值、并且参数难以选取的缺陷。为了验证算法的有效性，利用SGD(stochastic gradient descent)、带Nesterov动量的SGD、Adagrad算法对神经网络进行优化，实现顾客满意度预测与Adam算法进行对比。

1 质量成本三级科目建立

目前建材装备制造企业不仅对于质量成本的概念很模糊，没有设立专门的质量成本会计科目，混淆生产成本和质量成本概念并且忽略对质量成本的预测。笔者从建材装备制造企业全生命周期进行分析，包含原材料采购，产品研发设计、产品生产、产品销售、产品售后阶段，从这几条主线并考虑满意度的基础上来分析影响质量成本的主要因素，并对质量成本科目进行分析。在产品的全生命周期中，影响质量成本的5个因素主要是操作者自身专业素质和对质量的理解，机器设备的精度和先进性，加工生产方法和工艺流程的合理性，原材料的物理化学性能，生产厂房的温度、湿度、杂质、照明等环境因素，概括起来称为“人、机、法、料、环”。利用鱼骨图分析法从这5个方面来描述建材装备制造企业质量成本的主要影响因素。质量成本分析鱼骨图如图1所示。

图1 质量成本分析鱼骨图

从建材装备制造企业全生命周期进行分析，建材装备制造企业基于顾客满意度的质量成本构成如图2所示。

图2 考虑顾客满意的质量成本3级科目

2 基于Adam神经网络顾客满意度建模

2.1 基于Adam神经网络顾客满意度相关分析

在顾客的需要转化为顾客满意的过程中，当从一个步骤到下一个步骤的信息被丢失或歪曲时，将会产生实际质量与顾客预期质量的差距。在产品全生命周期，不充分的市场调研活动可能会误解真实的顾客需要和期望；由于产品和服务的设计者能力有限，可能会设计出不能正确反映顾客需要的标准；生产部门的活动可能会不符合标准。笔者基于考虑顾客满意度的质量成本因素，从前期准备成本、质量设计成本、质量管理成本(传统的质量成本内容，包含预防成本、鉴定成本、内部质量损失成本、外部质量损失成本)、质量服务成本、间接质量损失成本、外部质量保证成本、员工质量成本作为预测顾客满意度的神经网络输入层的指标，各项指标如表1所示，因此神经网络的输入层为10个节点。

假定影响顾客满意度CS的基本因素集为：V=(v1,v2,…,vn)，并且约定所有的因素相互独立。将顾客满意度指标划分为5级，采用市场调查和专家打分相结合进行量化，量化结果如表2所示。

S为基本因素的量化集，S=(s1,s2,…,sn)。W为基本因素的权重，W=(w1,w2,…,wn)。因此，顾客满意度CS=S·WT=s1w1+s2w2+…+snwn。

2.2 Adam神经网络顾客满意度预测模型设计

基于Adam神经网络的顾客满意度预测模型主要分为3个阶段：第一阶段是数据处理阶段；第二阶段是Adam神经网络结构设计及参数选择；第三阶段是进行Adam神经网络训练。Adam训练神经网络主要是在局部优化阶段，使用Adam代替SGD，让训练能够自适应地为每个参数计算学习率，降低学习率等参数的选取对算法性能的影响，让算法实施更加简单，性能更加稳定。

表2 顾客满意度分值

Adam神经网络的流程和步骤如下：

(1)数据处理。为了防止因奇异样本数据的存在而可能引起的网络训练时间增加，网络无法收敛等问题，在训练之前对样本数据集进行归一化处理。样本数据的归一化计算公式为：

(1)

式中：x为未归一化的一个样本数据；x*为归一化后的一个样本数据；xmin为样本数据的最小值；xmax为样本数据的最大值。

(2)神经网络结构设计及参数选择。BP神经网络是一种由前端输入层、中间隐含层、输出层3层结构组成的基于误差反向传播算法的多层前馈网络。其拓扑结构如图3所示。

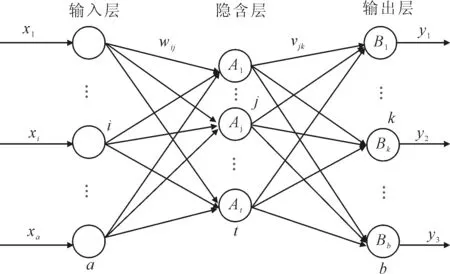
图3 神经网络拓扑结构图

笔者研究的基于质量成本的顾客满意度预测，输入是质量成本的10个指标，故网络的输入层节点(神经元)个数即为10个。而网络的输出值即为顾客满意度，故网络的输出层节点(神经元)个数为1。因为隐层数为1的神经网络已被证明在不限制神经网络节点数的同时，可以实现任意非线性映射而且训练时间相对短，精度能够达到要求。故选用单隐含层的网络。

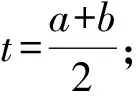
本文的顾客满意度预测神经网络的输入层节点数为10，输出层节点数为1，即a=10，b=1。根据上述公式计算可知隐含层节点数t的范围为[3，14]，经过试验对比分析，当t=8，神经网络的学习能力最强，故确定神经网络的隐含层节点数为8。即选择的输入节点数为10，隐含层节点数为8，输出层节点数为1的三层神经网络。

顾客满意度预测问题实际是一种广义多元回归问题，将神经网络的误差函数设为MSE，选择均方误差作为衡量网络可靠性的目标函数。其计算公式如下：

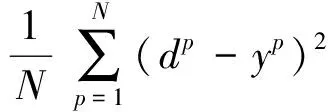
(2)

为了使神经网络具有强大的拟合能力，在网络的隐含层和输出层加入激活函数对神经元的输出进行映射。常用的激活函数有linear，sigmoid，tanh等。针对顾客满意度问题，笔者通过实验比较，选择tanh函数为隐含层与输出层的激活函数，该函数不仅具有软饱和性，能避sigmoid会产生的梯度消失问题，并且tanh收敛速度比sigmoid 更快。tanh计算公式如下：

(3)

(3)Adam神经网络模型学习及训练。Adam神经网络的训练包括以下几个步骤：

①网络初始化。用ωij表示输入层节点i到隐含层节点j的权值，vjk表示隐含层节点j到输出层k的权值；用Aj表示隐含层第j个神经元的阈值，用Bk表示输出层神经元的阈值。给各权值分别赋一个区间[-1,1]内的随机数，设定误差函数e，给定计算精度值ε和最大学习次数M。

②隐含层输出计算。根据输入变量X，输入层和隐含层间连接权值wij以及隐含层阈值a，计算隐含层输出H。

设输入变量X=(x1,x2,…，xa)，隐含层变量H=(h1,h2,…，ht)，输出层变量Y=(y1,y2,…，yb)，期望输出变量O=(o1,o2,…,ob)，则根据输入，隐含层每个节点的输出为：

(4)

式中：t为隐含层节点数；f为激励函数。

③输出层输出计算。根据隐含层输出H，连接权值vjk和阈值b，计算神经网络预测输出Y。计算公式如下：

(5)

④根据网络预测输出Y和期望输出O，利用式(2)计算网络预测误差MSE。

(6)

式中：N为样本数。

⑤权值更新和阈值更新。计算出误差后根据误差反向传播，不断调整权值和阈值，使误差不断地减少，直到MES<ε时，训练结束。

基于梯度下降法BP神经网络存在局部极小值，如果学习率过小或者激活函数倒数很小会使得权值、阈值更新速度变得很慢，网络的收敛速度也会很慢，因此利用Adam优化算法对权值和阈值进行优化更新。

Adam是一种可以替代传统随机梯度下降过程的一阶优化算法，它能基于训练数据迭代更新神经网络权重。Adam算法根据损失函数对每个参数的梯度的一阶矩估计和二阶矩估计动态调整每个参数的学习速率。Adam也是基于梯度下降的方法，但是每次迭代参数的学习步长都有一个确定的范围，不会因为很大的梯度导致很大的学习步长，参数值比较稳定。Adam算法与Adadelta算法和RMSprop算法一样存储了过去梯度的平方指数衰减平均值vt，也像Momentum算法一样保持了过去梯度指数衰减平均值mt，类似物体运动时的惯性，在更新时一定程度上保留之前的更新方向。计算公式如下：

mt=β1mt-1+(1-β1)gt

(7)

(8)

式中：mt为当前梯度的一阶矩(均值)估计；vt为当前梯度的二阶矩(有偏方差)估计；gt为当前梯度值；β1、β2为系数。

(9)

(10)

经过校正后最终Adam算法的更新公式如下：

(11)

式中：β1的默认值为0.9；β2的默认值为0.999；η为学习率；ε的默认值为10-8。

Adam神经网络流程如图4所示，Adam神经网络参数如表3所示。

3 实例分析

质量成本的10项指标所对应的费用通过对建材装备制造企业质量成本数据进行整理归类得到。由于建材装备制造企业重视产品质量和服务质量，因此笔者在影响顾客满意度基本因素中选取产品质量、售后服务这两个因素进行市场调查，根据市场调查选取两者的权重分别为0.6，0.4。最后得到质量成本对应顾客满意度数据如表4所示。

图4 Adam神经网络流程图

表3 Adam神经网络参数表

表4 质量成本与顾客满意度数据

表4中P1到P10指标分别代表质量管理成本(传统的质量成本内容，包含预防成本、鉴定成本、内部损失、外部损失)、前期准备成本、质量设计成本、质量服务成本、间接质量损失成本、外部质量保证成本、员工质量成本，CS代表对应的顾客满意度值。

对于当前建立的顾客满意度预测模型，使用python语言在基于Theano的Keras高层神经网络API下分别使用4种算法局部优化神经网络，分别是SGD、带Nesterov动量的SGD、Adagrad、Adam优化算法。局部优化阶段各算法收敛曲线如图5所示，各算法性能对比如表5所示，各算法训练集和测试集拟合度分别如图6～图13所示。

从表5可以看到评价指标均方误差值从SGD优化算法0.233降到Adam算法的0.003。由于Adam通过计算梯度的一阶矩估计和二阶矩估计而为不同的参数设计独立的自适应性学习率的这种方式，相比一般的自适应学习率方法能更好地提高神经网络收敛速度和收敛效果。与其他3种优化算法相比，采用Adam算法优化神经网络算法收敛速度更快，可以得到更高的收敛精度。

由表5、图6～图13可知，对训练集和测试集的拟合优度从SGD到Adam优化算法，拟合优度从0.801 32，0.862 73提升到0.969 04，0.968 72，拟合程度很高，精度高。并且从SGD算法，Adagrad算法，SGD(Nesterov)到Adam优化算法，拟合度是依次提高，说明改进学习率和更新权值的研究结果越来越好。采用Adam优化神经网络可以最小的收敛误差和最快的收敛避免训练进入局部最优点，能有效提高训练的精度和对数据集的拟合优度。说明在企业实际应用中对于顾客满意度预测取得了良好的效果。

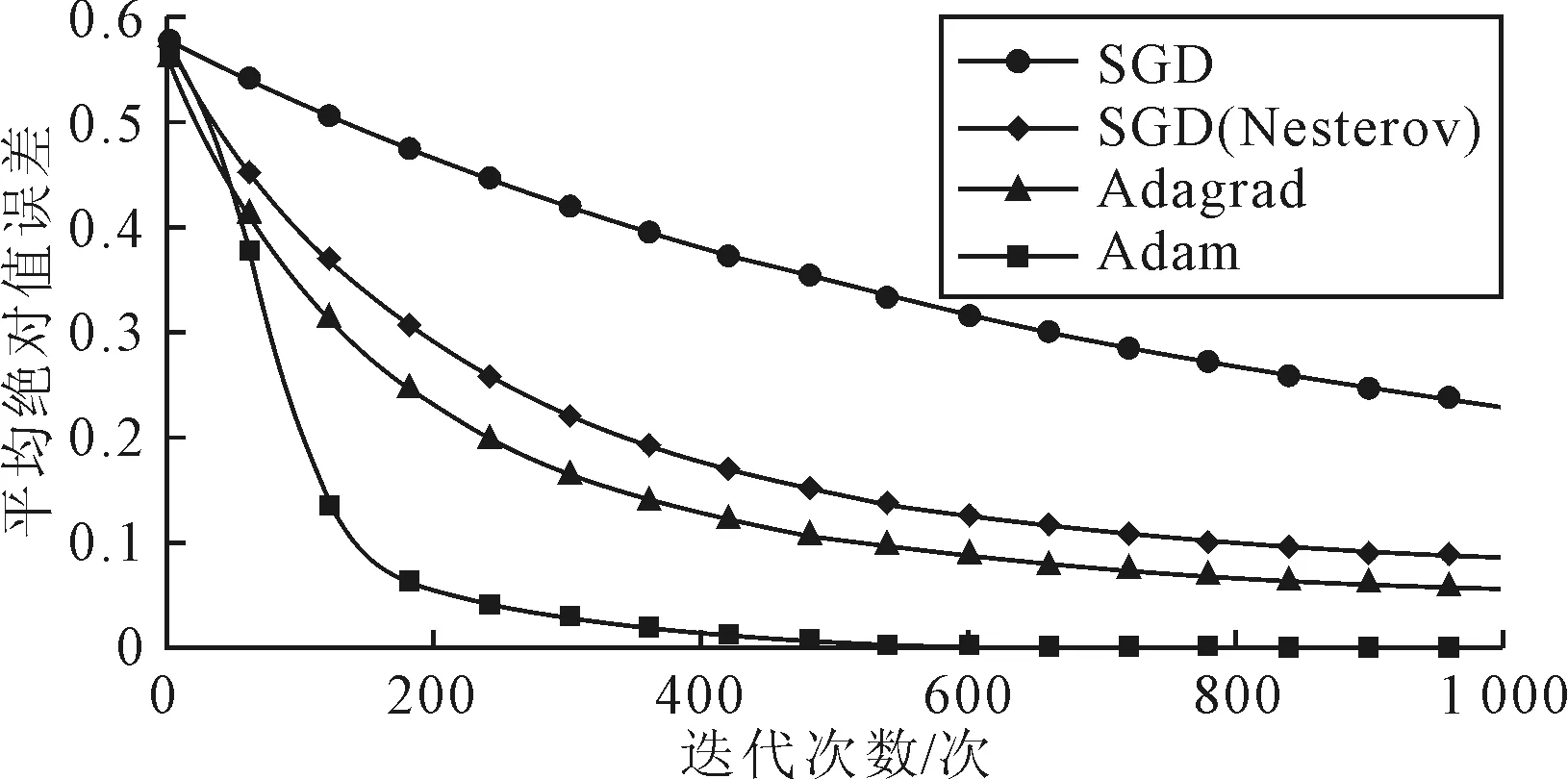
图5 训练集各算法收敛曲线

表5 各算法性能比较

图6 Adagrad神经网络训练拟合度

图7 Adagrad神经网络测试拟合度

图8 SGD神经网络训练拟合度

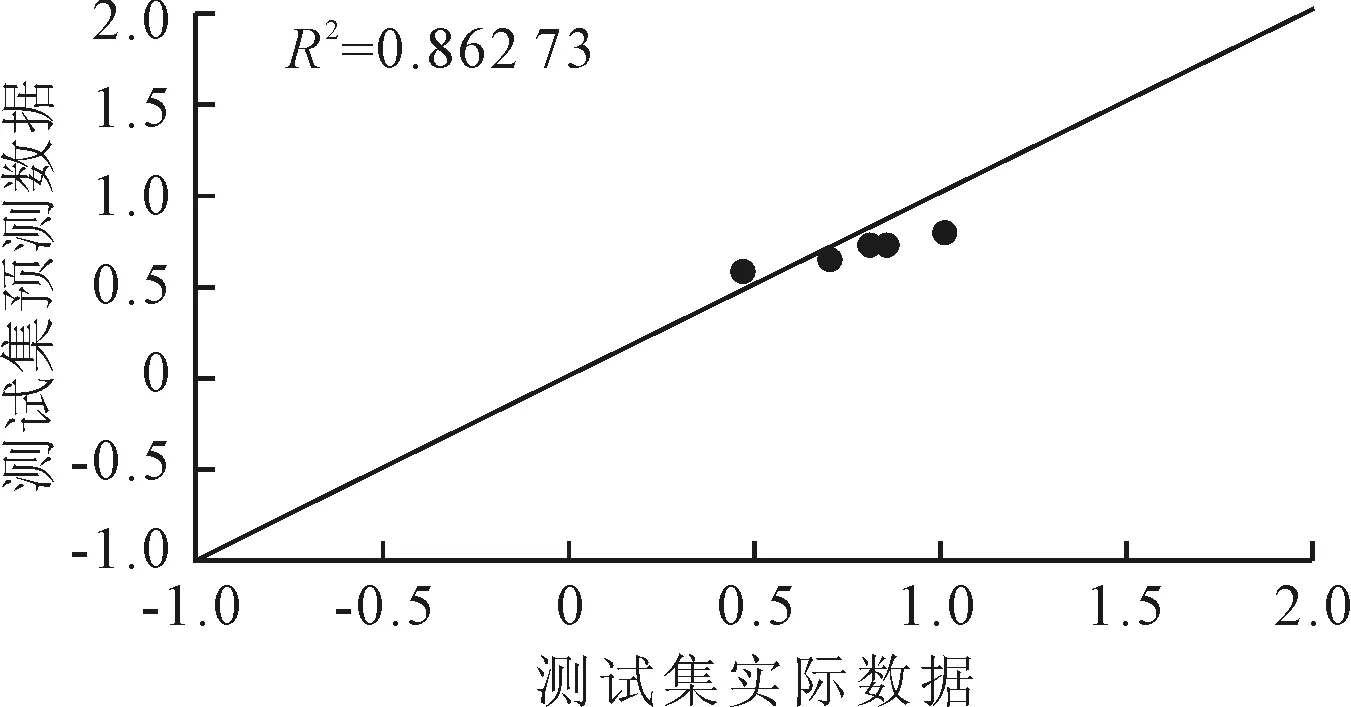
图9 SGD神经网络测试拟合度

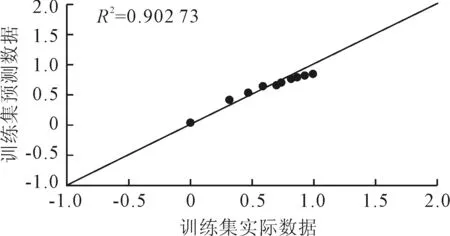
图10 SGD(Nesterov)神经网络训练拟合度

图11 SGD(Nesterov)神经网络测试拟合度

图12 Adam神经网络训练拟合度

图13 Adam神经网络测试拟合度

4 结论

在文献研究的基础上，针对性地创建了符合建材装备制造企业实际的考虑顾客满意度的质量成本3级科目；提出了基于Adam神经网络的顾客满意度预测模型，以某建材装备制造企业的实际顾客满意度问题实例进行实验分析，与SGD、带Nesterov动量的SGD、Adagrad、Adagrad优化算法进行对比分析。结果表明，基于Adam神经网络的顾客满意度预测模型更能有效地预测顾客满意度，通过这种事前预测，能更好地指导企业对整个产品生命周期进行质量管理和成本管理。