斜交网格筒结构侧向刚度影响因素研究

桑 丹

(陕西国防工业职业技术学院 陕西 西安：710300)

目前，国内外已有多例斜交网格筒结构体系的工程实例。斜交网格筒结构最早出现在1960年左右在匹兹堡建成的IBM大厦，如图1(a)所示。在国内，斜交网格筒结构体系也已有许多工程实例，首次在超高层建筑中采用钢管混凝土斜交网格筒中筒结构体系的就是广州西塔，如图1(b)所示，它具有较大的抗侧刚度以及良好的抗震性能。

图1 典型斜交网格筒高层建筑

斜交网格筒结构是由水平环梁和斜向布置的交叉斜柱组合而成，它与传统的垂直梁柱结构形式完全不同[1-2]。斜交网格筒结构主要依靠斜交网格筒中的杆件轴力来抵抗外荷载，使构件承载力得到充分地发挥，有较大的抗侧刚度，该新型结构体系为高层及超高层建筑的发展提供了有利的条件[3-4]。目前，斜交网格筒结构的力学性能研究滞后于工程实际应用，所以对此类新型结构体系进行侧向刚度影响因素研究具有重大意义。

1 模型选取及分析方法

建立斜交网格筒模型，层高为4m，平面为36m×36m的正四边形，斜柱为钢管混凝土，钢材采用Q345，混凝土为C40。未特殊说明的情况下，模型中各层环梁均采用H型钢H400×300×10×16，斜柱与斜柱以及斜柱与水平环梁的相交节点采用刚性连接。利用SAP2000结构分析软件对斜交网格筒结构进行侧向荷载作用下的静力弹性分析，找出影响斜交网格筒结构侧向刚度的主要因素。

斜交网格筒结构的几何布置如图2所示。图2仅截取了结构的一个模块，结构的宽度B均为36m，结构的高度H在后续的分析模型中，针对不同的因素有不同的取值，均有所表述。

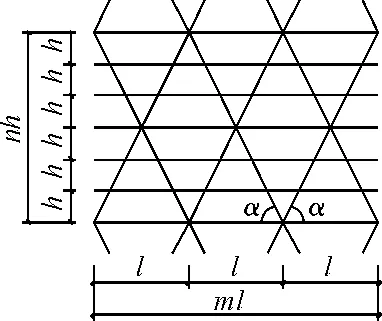
图2 几何布置图

由图2中各几何参数之间的关系，认为影响斜交网格筒结构抗侧刚度的几何因素为斜柱角度α、结构的高宽比H/B以及主环梁跨数m。

2 侧向刚度影响因素

2.1 斜柱角度

经研究发现，斜交网格筒结构的抗侧刚度比传统框筒结构的抗侧刚度大[2]。对于斜柱的角度α=90°的结构，可以认为其是传统的框筒结构。斜柱角度α在35°附近时，斜交网格筒的抗剪刚度最大；斜柱角度α为90°时，其抗弯刚度最大。所以，在35°～90°之间，随着斜柱角度α的逐渐增大，侧向剪切刚度在逐渐减小，侧向弯曲刚度在逐渐增加。那么，一定存在着一个最优的角度值，使得斜交网格筒结构的抗侧刚度达到最大。

对于N为30、45、60、75、90层的模型，主环梁跨数均为m=3，改变斜柱角度α为34°、53°、63°、69°、73°、76°、83°分别进行对比分析，图3给出了30层的结构模型。改变α值，模型中斜柱的长度也会随之发生变化。为便于比较，根据斜柱用钢量M相等、杆件径厚比相近的原则，以α=69°时的斜柱截面为基准，径厚比控制在30左右，计算其余各斜柱的截面尺寸：M=Ah/sinα(A—斜柱横截面积，h—楼层高)。

图3 不同斜柱角度的结构模型(N=30，m=3)

图4中(a)-(e)分别为相同结构宽度(36m)，不同的楼层数(即不同结构高度)下，改变斜柱角度的顶点位移。不同斜柱角度下结构的顶点位移曲线如图4所示，由图4可知：

(1)当N=30时，除了34°和83°，其余5种角度下结构的顶点位移值相近。当α值在53°～76°范围内时，斜柱角度对结构抗侧刚度的影响不大。

(2)随着高宽比增大，α对结构抗侧刚度的影响逐渐明显。结构最大抗侧刚度对应的α值(即斜柱角度最优值)随着结构高宽比的增大而出现上升的趋势，如楼层数N为30、45、60、75、90时对应的斜柱角度最优值分别为63°、63°～73°、69°～73°、73°、76°。

(3)在α最优值附近的角度，使得结构具有相近的抗侧刚度，所以可以认为斜柱角度的最优值是处在某一区间范围的角度值。当楼层数N为30、45、60、75、90时对应的α最优值区间分别为53°～63°、63°～73°、69°～76°、69°～76°、73°～76°。由此可见，随着结构高宽比的增大，结构最大抗侧刚度对应的斜柱角度最优值区间在上移。

2.2 结构高宽比

为了分析高宽比对结构抗侧刚度的影响，对5种不同高宽比(分别为3.3、5、6.7、8.3、10)的结构进行对比，保持结构平面不变、主环梁跨数m=3，楼层数N分别为30、45、60、75、90。

斜柱角度α=73°时，各高宽比的结构侧移曲线如图5所示。由图5可知：斜交网格筒结构高宽比较小时，结构侧向变形主要为剪切型；当结构的高宽比较大时，其侧向变形主要为弯曲型。随着结构高宽比的增大，其对抗弯刚度的需求在不断增强，而对抗剪刚度的需求在减小。斜交网格筒结构的抗弯刚度主要取决于斜柱轴向刚度沿竖向的分量；其抗剪刚度主要取决于斜柱轴向刚度沿水平方向的分量。

高层建筑中，随着建筑物高度增加，剪力和弯矩都在增大，但是两者增加的幅度明显不同。其底部的剪力呈线性增长，而弯矩增长迅速。因此在实际工程中，可以根据结构的高度对斜交网格筒中的斜柱采用变角度布置，以满足结构在不同高度处对抗侧刚度的需求。

图4 斜柱角度对结构侧移的影响

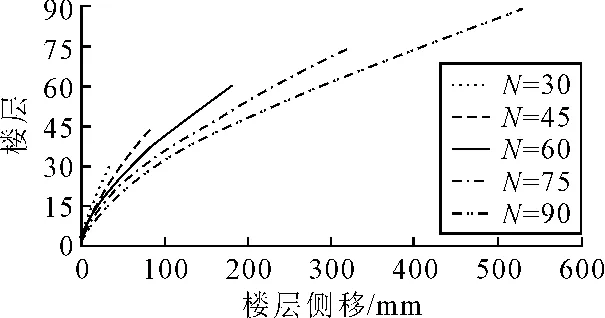
图5 高宽比对结构侧移的影响

2.3 主环梁跨数

建立4组模型，主环梁跨数m分别为3、4、5、6，结构平面为36m×36m的正四边形保持不变。模型建立过程中，保证4组模型每层斜柱的用钢量相等，而且保证圆管截面的径厚比在30左右。

不同主环梁跨数的结构顶点位移曲线如图6所示。由图6可知：对于m=3，α=73°；m=4，α=74°；m=5，α=73°；及m=6，α=76°的结构，α值对结构抗侧刚度的影响较小，4组模型的α值比较接近而且各自均处在其最优值附近。

为了分析主环梁跨数及结构高宽比对结构抗侧刚度的影响，对比在N为30、45、60、75时，m=3，α=73°；m=4，α=74°；m=5，α=73°；及m=6，α=76°的顶点侧移情况，其结构模型图如图7所示。不同主环梁跨数的结构顶点位移情况如图8所示，在α值较接近的情况下，m值改变对结构的顶点位移影响很小。

虽然主环梁跨数m对结构的抗侧性能影响很小，但是不同的m值会改变环梁的跨度及相交节点的数目。当主环梁跨数m较大时，会导致环梁的跨度较小、各种构件及节点数量较多，从而使得施工起来比较麻烦而且材料用量也比较浪费；当主环梁跨数m较小时，会导致环梁跨度较大，使得其材料用量明显加大。因此，实际工程中m的取值要综合考虑建筑美观、施工难易程度及材料用量等方面的因素，从而确定出合理的主环梁跨数。

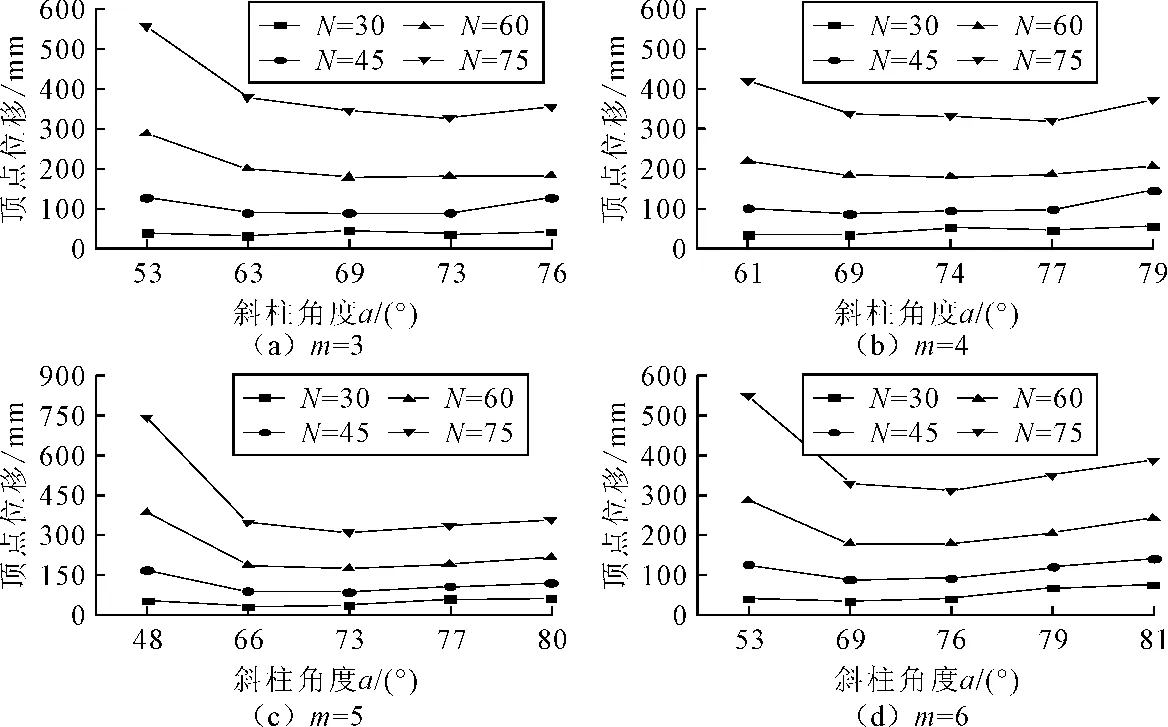
图6 不同主环梁跨数的结构顶点位移

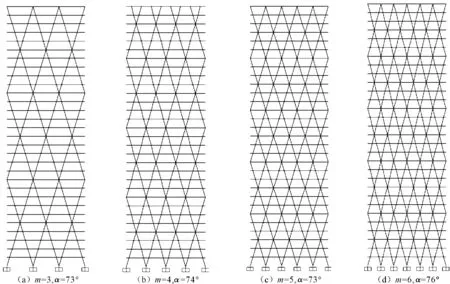
图7 不同主环梁跨数结构模型(30层)

图8 主环梁跨数对结构侧移的影响

2.4 斜柱和环梁的相对刚度

为了考虑斜柱和环梁的相对刚度对斜交网格筒结构抗侧性能的影响，对于楼层数N=60，α=69°，m=3的结构模型，斜柱截面保持不变，改变环梁的尺寸。环梁分别采用H300×200×8×12、H400×300×10×16及H500×300×11×15，在侧向荷载作用下，对应的结构顶点位移分别为179.0mm、178.9mm及178.7mm，如图9所示。由图9可知，在其他条件相同的情况下，改变斜柱和环梁的相对刚度，结构的顶点位移几乎不发生改变，说明环梁刚度改变对结构抗侧刚度影响很小。

图9 斜柱和环梁的相对刚度对结构侧移的影响

2.5 角柱

对于结构平面为四边形的斜交网格筒结构，其转角处的环梁为悬挑状态，可以通过在转角处增设竖向角柱，使得结构构件自然过渡，增强了结构的整体性。对于楼层数N=60，斜柱角度α=53°，主环梁跨数m=6的结构模型，受拉翼缘立面底层柱在有无角柱情况下的轴力对比如图10所示，结构侧移曲线对比如图11所示。由图11可知：

(1)对于无角柱的结构，其立面中部的斜柱轴力较小，角部的斜柱轴力较大，各斜柱轴力分布整体较为均匀，结构顶点位移为286mm。

(2)对于增设角柱(截面尺寸与斜柱相同)的结构，斜柱轴力分布均匀，其值较无角柱状态下降低了约20%；但是角柱轴力值较大，约为中间斜柱的1.7倍；结构顶点位移为232mm。

由以上分析可知，在结构角部增设角柱，可以提高结构的抗侧刚度、降低斜柱轴力，但同时会引起角柱应力集中现象。

图10 角柱对斜柱轴力的影响

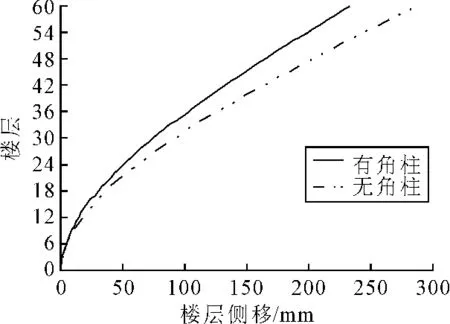
图11 角柱对结构侧移的影响

2.6 杆件连接形式

在前述的分析模型中，斜柱与斜柱及斜柱与水平环梁相交节点均采用刚性连接，把这种连接形式称为刚接。为了分析不同杆件连接形式对结构抗侧性能的影响，将斜柱两端铰接、环梁固支于斜柱的连接形式称为铰接[5]。

对于楼层数N=60，斜柱角度α=69°，主环梁跨数m=3的结构模型，采用静力弹性分析方法，得到斜柱在刚接情况下结构的顶点位移为179mm，铰接时为180mm，其侧移曲线如图12所示。受拉翼缘立面中的底层斜柱，在铰接状态下，其最大、最小轴力分别为3435kN和3228kN；在刚接情况下，其最大、最小轴力分别为3413kN和3205kN，斜柱的杆端弯矩为46kN·m，弯矩值很小可忽略不计，可认为其等同于斜柱两端铰接。由上述分析可知，斜柱两端杆件的连接形式对其抗侧刚度影响很小，实际工程中对于杆件的连接以便于施工为原则。

图12 杆件连接形式对结构侧移的影响

3 小结

本文通过对斜交网格筒结构抗侧刚度影响因素的研究，得到了以下主要结论：

(1)随着结构高宽比增大，斜柱角度对结构抗侧刚度的影响逐渐明显，斜柱角度的最优值区间整体上移。斜交网格筒结构高宽比较小时，结构侧向变形主要为剪切型；当结构的高宽比较大时，其侧向变形主要为弯曲型。

(2)主环梁跨数、环梁的相对刚度以及杆件的连接形式等对斜交网筒结构的抗侧性能影响很小，实际工程中的取值要综合考虑建筑美观、施工难易程度及材料用量等方面的因素。在结构角部增设竖向的角柱，虽然可以增大结构的抗侧刚度，但是同时也会引起应力集中现象，应慎重考虑。