航空发动机转子轴承运行可靠性评估方法

陈保家,邱光银,肖文荣,田红亮,陈法法,赵春华,刘芙蓉

(三峡大学湖北省水电机械设备设计与维护重点实验室,443002,湖北宜昌)

航空发动机作为飞机的心脏,其健康水平直接决定飞机的寿命和飞行的安全,而作为发动机的关键零部件,主轴承失效所引起的故障往往会对发动机乃至飞机产生灾难性的后果[1]。在1986年至1992年的6年时间里,CFM56-3发动机高压压气机滚珠轴承失效占发动机空中停车事件的25%,在各种原因中居首位[2]。RB211-22B发动机在投入航线使用的半年多时间内,其风扇转子的中介滚珠轴承接连发生了5起滑蹭损伤失效[3]。我军的航空发动机均发生过主轴承故障,以某型现役军用发动机为例,空军的外场使用统计表明,由于主轴承失效造成的飞行事故占机械系统总故障的19%左右[4]。航空发动机主轴承的工作条件极其恶劣,如何保障其安全可靠运行,预防和避免关键设备出现故障,杜绝重大和灾难性事故的发生,已成为当前科学研究和工业发展的重要研究课题之一。

传统的可靠度评估方法利用数理统计理论对产品大样本失效寿命数据进行统计分析,在描述时间、动态过程等方面存在困难,得到的是设备的整体可靠性[5]。针对复杂机电系统故障预示和安全保障问题,国内外学者们已经开始认识到系统运行状态信息在可靠性评估中的重要性。米兰理工大学的Zio指出,状态信息的引入将有效地提高复杂系统可靠性建模的合理性和准确性[6]。西安交通大学何正嘉等详细阐述了以动态建模与故障机理分析、信号处理与故障特征提取为理论基础的机械设备运行可靠性的技术内涵,赋予运行可靠性新的含义,定义运行可靠度,提出基于机械设备状态信息的运行可靠性评估方法[7-9]。比例故障率模型(PHM)假设状态协变量对基本故障率函数具有乘法效应,有效地将状态信息用于设备可靠性评估与失效分析当中[10]。Ding等提出了一种基于设备状态振动特征的比例故障率模型可靠性评估的方法,将反映轴承运行状态特征的方均根、峭度指标与威布尔故障率模型之间建立联系,对轴承健康状态进行评估[11]。然而,PHM同样需要大量失效样本数据去估计模型中的基本故障率函数及各协变量的权重参数,当协变量发生大的波动时,会对PHM模型的预测准确性产生较大的影响。Sun提出了比例协变量模型(PCM)[12],通过基本协变量函数,响应协变量可对系统故障率函数进行不断更新,揭示了状态监测数据与设备运行安全性和可靠性的动态映射关系,并分别以磨屑中铁粒子的质量分数和齿轮振动信号的峭度指标作为响应协变量,利用PCM模型对发动机和齿轮裂纹故障率进行建模和可靠性评估。

在以上两个应用实例中,设备的初始故障率函数仍然需要通过大样本的失效寿命数据求得。对于少失效数据或零失效数据的情况,Sun指出可根据操作者的经验或其他补充信息确定设备的基本协变量函数,但该方法会将人的主观差异性带入PCM当中,使评价的波动性变大,从而影响评价的准确性[13]。逻辑回归模型(LRM)不要求变量满足误差分布趋于正态分布假设,可在一系列状态特征参数表征下给出事件发生的概率,这种思想与可靠性评估思想是相吻合的[14]。

为了完善PCM在少失效数据或零失效数据情况下的工程实用性,本文提出了一种基于LRM的响应协变量初始故障率函数求解方法,该方法不需要大样本失效数据,只需知道不同响应协变量对应的设备状态即可,也不需要人为确定基本协变量函数,避免了人为主观因素带入的估计偏差。通过对航空发动机转子轴承疲劳寿命试验过程中的振动信号分析,验证了该方法的有效性。

1 比例协变量模型

PCM模型有两个假设前提:一是响应协变量函数与系统的故障率成比例,这个与PHM的假设前提是一致的,并且在Sun的论文中得到了实验验证[12];二是系统的响应协变量是系统故障率的连续单调函数。PCM模型的形式定义为[12]

ψ(Zr(t))=C(t)h(t)

(1)

式中:ψ(Zr(t))为响应协变量函数,反映设备的运行状态;Zr(t)为响应协变量;C(t)为基本协变量函数,表征系统的故障率函数与响应协变量之间的关系;h(t)表示系统的故障率函数。本文只研究最简单的单响应协变量的情况,用Zr(t)来代替ψ(Zr(t)),则式(1)可简化为

Zr(t)=C(t)h(t)

(2)

由式(2)可以看出:Zr(t)的选择对准确估计设备的h(t)十分重要,Zr(t)要能实时地反映设备的运行性能,揭示其退化过程,可直接从监测数据中获取,如温度、压力、油液中金属粒子的含量等,或是从其他信号中提取的相应的特征参量,如振动信号的均值、均方值、小波能量、信息熵等;C(t)表示Zr(t)和h(t)的关系函数,常用的基本协变量函数有多项式函数、幂函数模型、指数函数等,可以通过回归分析方法(RAM)拟合得到[15]。

2 PCM可靠性评估过程

基于PCM进行设备可靠性估计的具体过程描述如下。

(1)假设设备历史失效寿命数据集为{Ti}(i=1,2,…,mf,mf为失效样品数),采用数理统计方法估计系统失效概率密度函数f(t)和初始故障率函数hin(t)。

(2)由初始故障率函数hin(t)和响应协变量函数Zr(t)估计基本协变量函数离散形式Ck,表示为

Ck=Zr(tk)hin(tk),k=1,2,…,mc

(3)

式中:mc为状态监测数据样本数。利用RAM拟合出基本协变量函数的连续表达式C(t)。如果没有完整的失效寿命数据,可以根据经验或其他补充信息确定Zr(t)与h(t)间的线性比例因子r,从而确定C(t)的表达式。

(3)用新的监测协变量{Zr(tj)}(j=1,2,…,mn)更新故障率函数,mn表示新的监测数据个数,更新公式为

i=1,2,…,mc,mc+1,mc+2,…,mc+mn

(4)

(5)

上述可靠性评估的流程如图1所示。

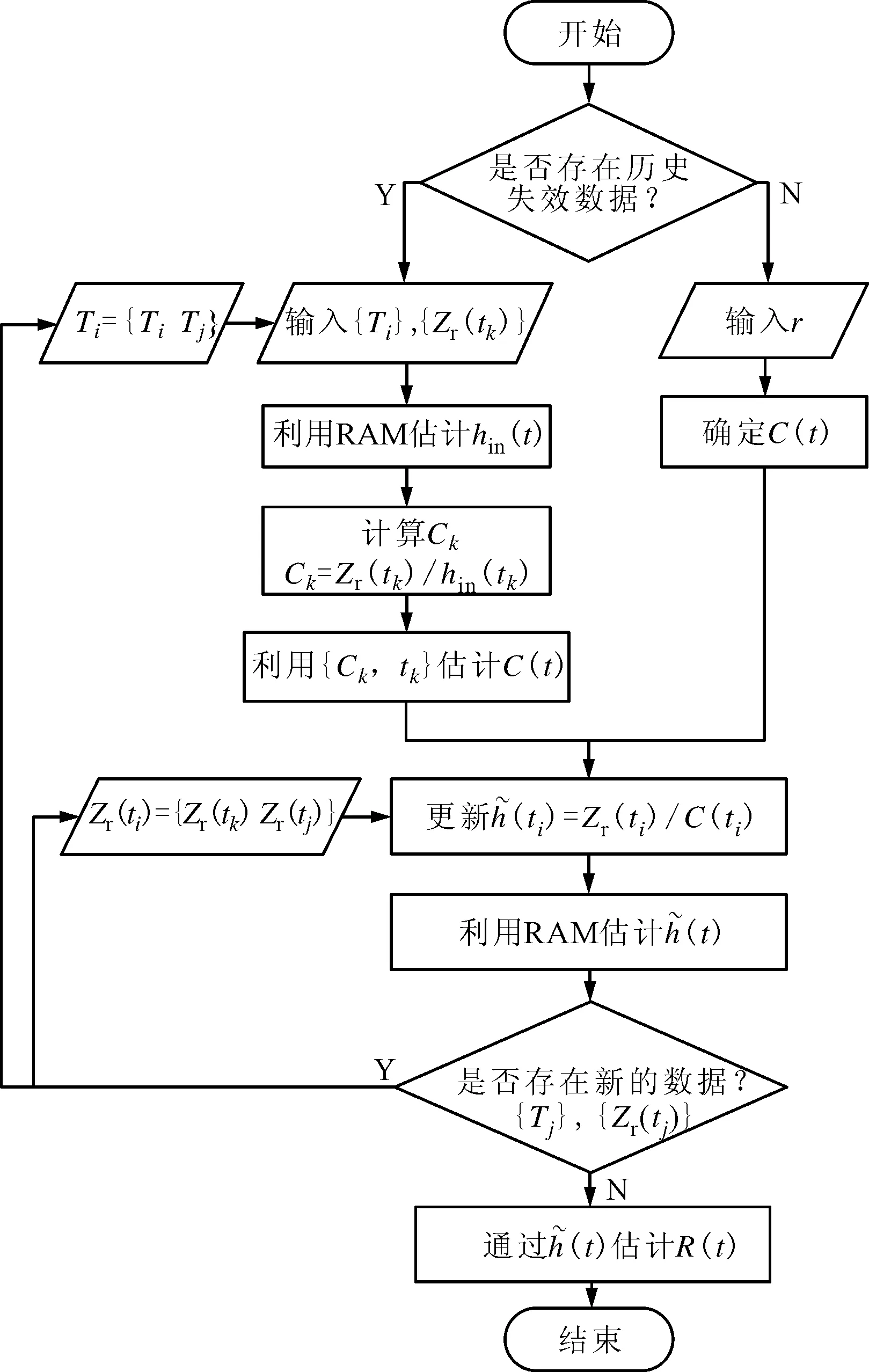
图1 基于PCM的可靠性评估流程图

3 Logisitc回归模型

假设在时刻ti,设备的状态特征可由一个k+1维向量Xi=[1,x1i,x2i,…,xki]T表示,设备状态为yi(正常时yi=1,否则yi=0),则设备的可靠度函数可表示为[14]

(6)

式中B=[β0,β1,…,βk]T,为模型参数向量,且β0>0。Logistic回归模型表达式为

(7)

式中:logit为Logistic回归模型运算符号。因为LRM是一个非线性模型,模型参数可以通过Nelder-Mead法求解其极大似然函数得到。模型的对数似然函数为

(8)

在确定模型参数后,模型的可靠度为

R(tj)=P(yj=1|Xj)=

(9)

4 改进的PCM可靠性评估方法

在利用PCM模型进行可靠性评估时,需要通过大样本失效寿命数据估计系统的初始故障率函数hin(t)[16],而机械设备失效是一个缓慢的退化过程,随着材料质量和工艺水平的提高,呈现出长寿命、变工况、结构复杂、多失效模式的特性,特别是对于单台或小样本设备,很难通过传统的方法获取大样本失效数据,PCM的这个要求极大地限制了其在机械领域的工程应用。基于Logistic回归模型的响应协变量初始故障率函数求解方法可直接针对设备运行过程中的监测数据,提取状态监测指标,并结合相关标准或实际操作中规定的失效阈值,通过Logistic回归模型先求解设备的R(t),再通过hin(t)=f(t)/Rin(t)=-d(lnRin(t))/dt进一步求解出设备的hin(t)。

图2是基于改进PCM的可靠性评估流程图。由监测数据求出系统的响应协变量序列{ti,Zri},将协变量作为LRM的输入变量,由Zri和它的失效阈值Zri确定系统的状态yi,正常时yi=1,否则yi=0,将状态变量作为模型的输出变量利用极大似然法对模型进行参数估计。建模完成后,利用其求解不同协变量值对应的Ri,与时间信息结合,进行回归分析拟合,求出hin(t),将其代入到PCM模型当中,完成章节2中的步骤(3)～(5),对系统进行可靠性评估。当Zr为多变量时,将上图中的X和Y变为多变量矩阵,仍然可以通过多变量LRM完成hin(t)求解。

图2 基于改进PCM的可靠性评估流程

5 应用实例

5.1 试验描述

本文可靠性评估数据是来源于美国辛辛那提大学智能维护中心的航空发动机转子轴承疲劳寿命试验[17]。试验台外观和结构如图3a和图3b所示,该试验台可以同时对4个航空发动机转子主轴承进行疲劳寿命试验,轴承通过油液润滑,在回油管上装有磁塞,监测铁屑含量,超过设定临界值时自动切断电路。试验过程中,轴的转速为2 000 r/min,并且通过弹性装置为轴承加径向载荷,径向载荷为26.6 kN。利用振动加速度传感器采集每个轴承水平和竖直两个方向的振动加速度信号,采样频率为12 kHz,采样时间间隔20 min,采样长度20 480点。本次研究的是data1中的3#和4#失效轴承,3#轴承(轴承A)失效类型为内圈故障,4#轴承(轴承B)失效类型为外圈与滚动体复合故障。该实验过程中只有4个轴承发生了失效,寿命差异很大,难以通过传统的数理统计方法准确估计轴承寿命分布。文中所用滚动轴承型号为ZA-2115,其具体结构参数如下:节径71.447 mm,滚子直径8.401 mm,滚子个数为16,接触角θ=15.17°。

(a)试验台外观

(b)试验台结构图3 轴承试验台及传感器布置情况

5.2 振动信号时域特征提取

轴承出现故障时,时域信号的幅值随轴承振动水平的增加而变大,振动信号的时域特征能够反映滚动轴承的状态[18-19]。常用的时域特征分为有量纲指标和无量纲指标两种,有量纲时域指标包括均值、均方根值、方差等,这些值随轴承故障程度的增加呈单调增长的趋势[20]。但是,有量纲指标对载荷和转速的变化比较敏感,其变化趋势易受工况的影响。无量纲指标基本不受转速、载荷等因素的影响,常用的无量纲指标有峭度指标、峰值指标、裕度指标等[21]。本文共提取了轴承振动信号11个时域指标,其名称和简写分别为:加速度均值xm、信号峰值xp、信号均方根幅值xra、加速度均方根值xrms、信号标准差xstd、偏斜度指标xske、峭度指标xk、峰值指标xc、裕度指标xmar、波形指标xsha和脉冲指标xi。

图4为轴承A的6个典型特征指标,由于采样频率不是严格的等间矩采样,因此图中以采样点序号代替采样的实际周期。另外5个指标都与这6个指标中的某个指标有相似的变化趋势,根据它们间的相似关系可分为6组,如表1所示。

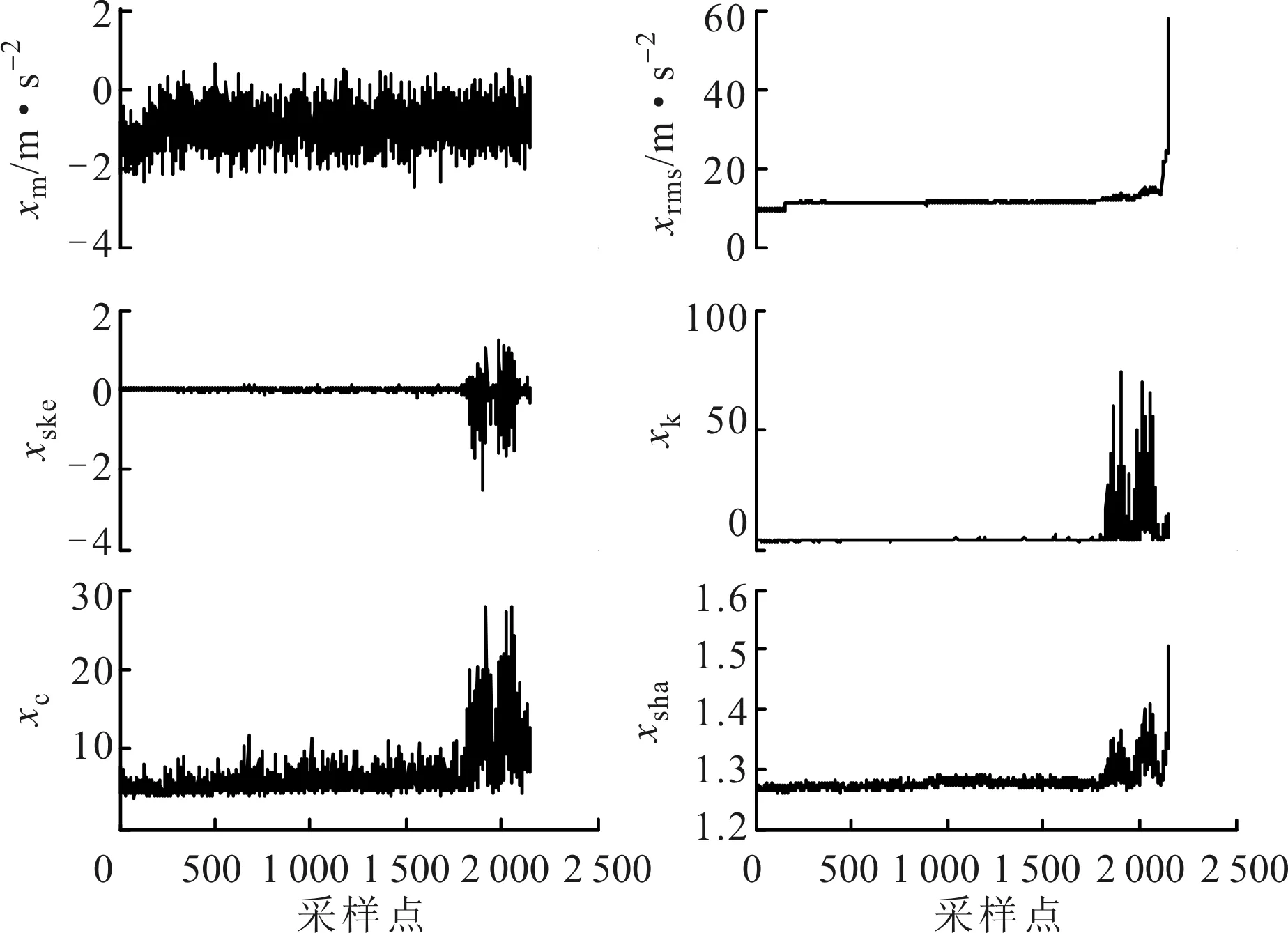
图4 轴承A的6个典型振动信号时域特征指标

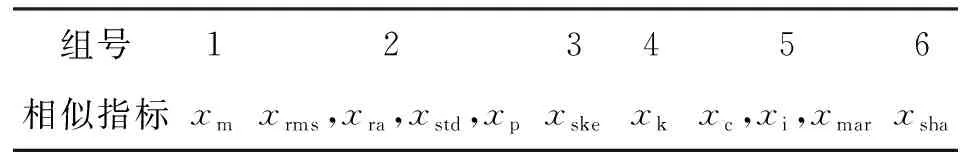
组号123456相似指标xmxrms,xra,xstd,xpxskexkxc,xi,xmarxsha

由图4可以观察到,随着轴承运转时间的增加,不同的时域特征表现出了不同的变化趋势:xm比较杂乱,没有明显的上升趋势;xrms噪声干扰较小,当轴承正常运转时,特征值变化缓慢,当轴承处于失效期时,特征值明显上升;xske没有明显趋势,幅值波动较小,在故障初期和失效期,发生剧烈波动,幅值明显增大;xk对冲击振动相当敏感,当轴承正常运转时,信号比较平稳,xk变化较小,当轴承进入早期损伤和扩展阶段时,xk明显增大且剧烈抖动,当轴承处于失效期时,xk指标又显著变小;xc受噪声干扰较大,存在很多毛刺,当轴承正常时,幅值较小,当轴承进入早期损伤、扩展期时,幅值明显增大,且存在两个明显的波峰;当轴承正常运转时,波形指标xsha有微小波动,幅值较小,随着轴承进入早期损伤阶段,幅值有一个明显的增大,出现一个小的波峰,随着损伤的扩展,幅值进一步增大,当轴承发生失效时,指标剧烈增加达到最大。

5.3 响应协变量选择

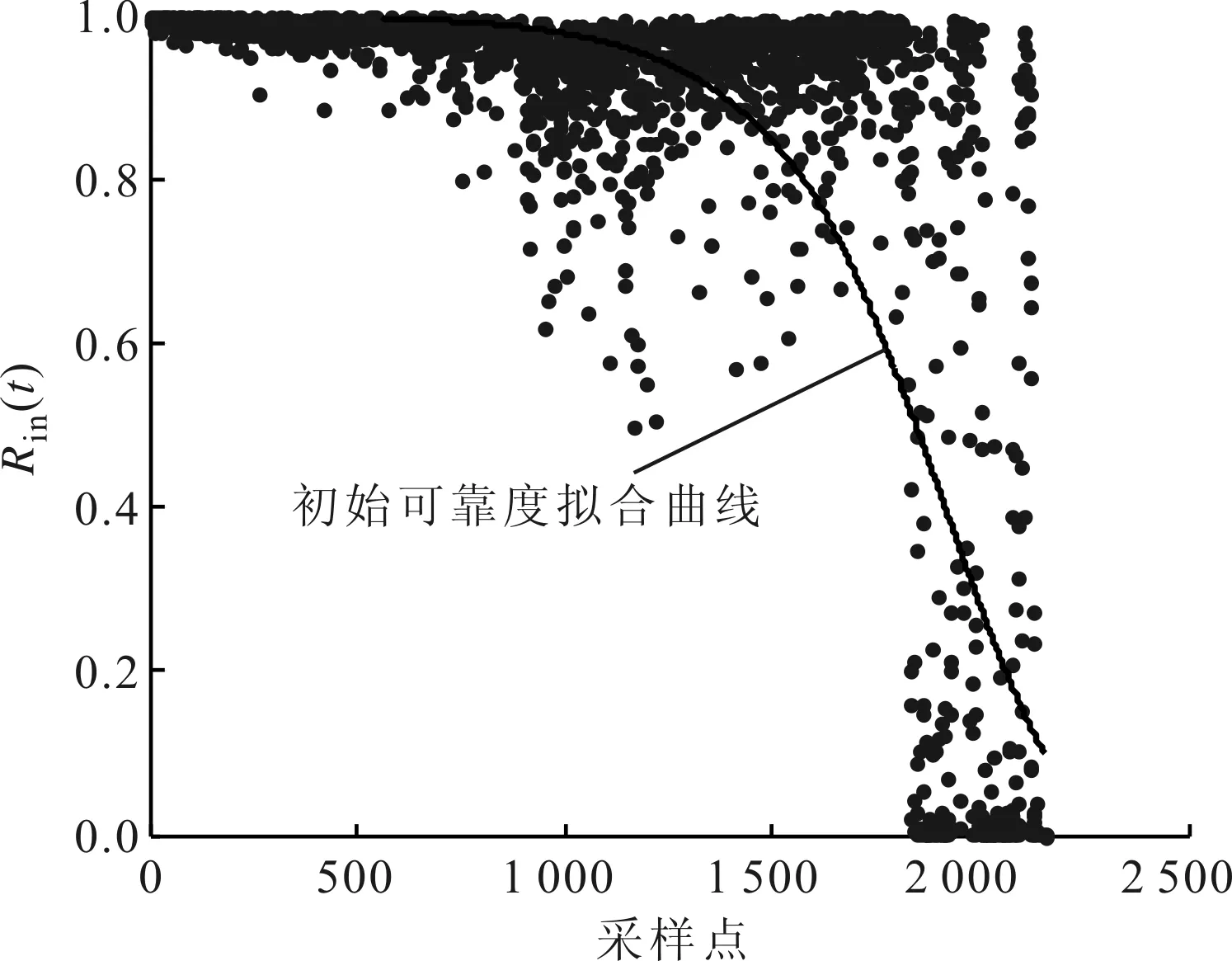
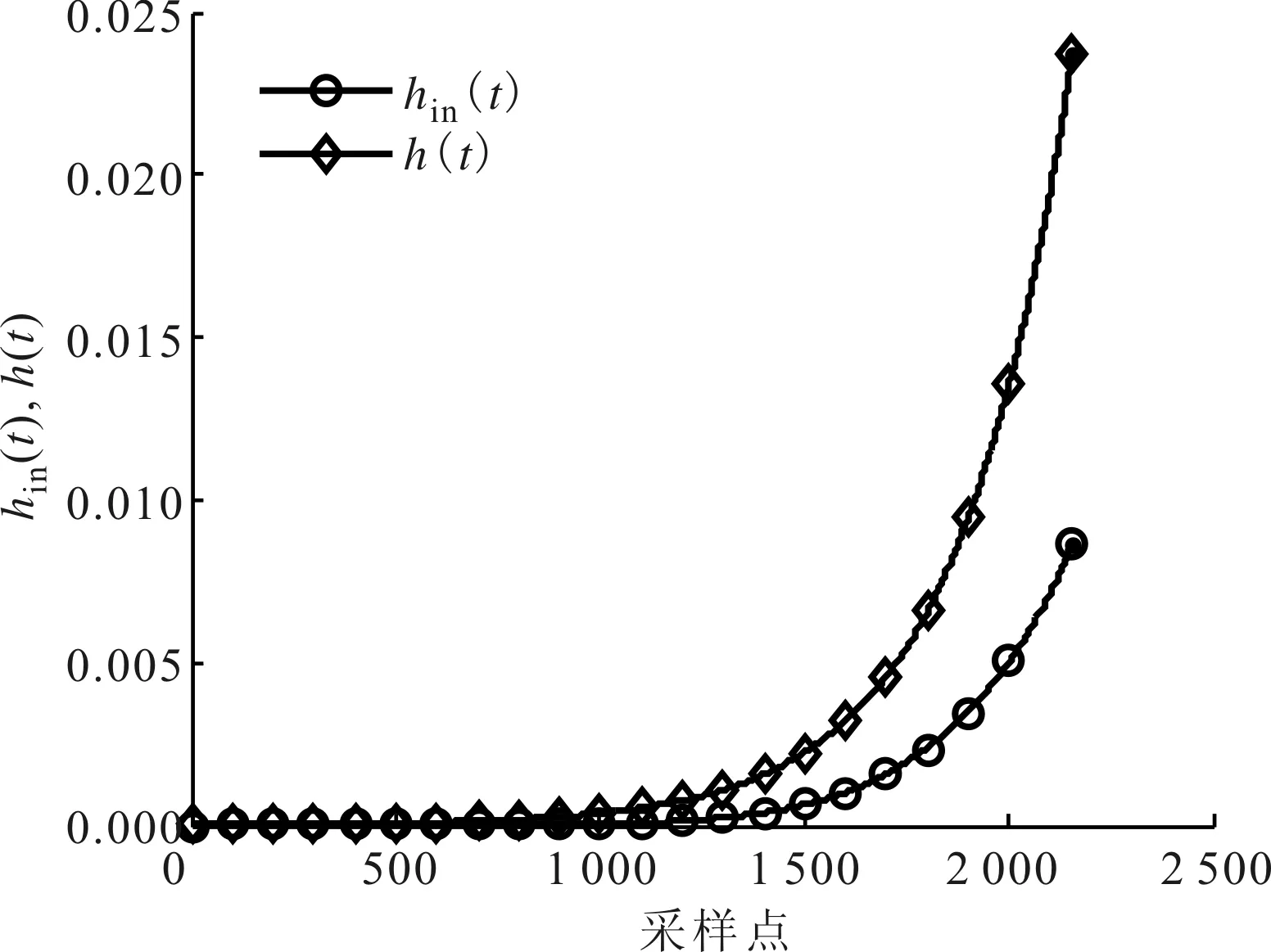
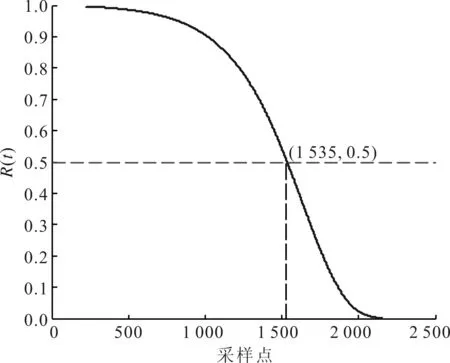
轴承正常运行时,各个指标的幅值都很小,且变化不大,当轴承处于初始故障期时,各特征值有缓慢上升,当轴承处于故障发展期时,特征值继续增大,并且有很大波动。除了xm外,其他时域指标都有一个逐渐增大的趋势,xrms趋势最好,但是对早期损伤敏感度不够,xk对早期损伤最敏感,但是故障趋势不明显,xc的敏感性和趋势性都较好,但是波动性太大,相对于以上几个指标,xsha的敏感性和趋势性都较好,而且波动性最小,因此本文将其选为可靠性评估过程中的响应协变量。每个轴承的寿命相差较大,与之相对应的是每个轴承协变量的变化也很大。图5所示为A、B轴承的xsha值,图中轴承的失效阈值xt(xt=1.35),xt要根据xsha数据变化趋势选择,当xsha

图5 轴承A、B的波形指标变化趋势

5.4 初始故障率及可靠性求解过程

以轴承A作为参考对象,将不同时刻ti所对应的波指标xshai组成响应协变量序列{xshai}作为LRM输入向量Xi,失效阈值xt=1.35,如果xshai

271.4-210.2xshai

(10)

将响应协变量序列{xshai}中的值代入式(10),可求出每个不同xshai值所对应的离散初始可靠度Rin(t),如图6中的散点所示。由于xshai本身的波动性及模型参数的影响,散点的分布很比较混乱,对其进行滑动平均拟合,结果如图6中实线所示,进一步求解出离散hin(t),并利用回归分析对其进行幂函数、指数函数和高斯函数模型拟合,各模型表达式及参数,各模型拟合优度比较分别如表2和表3所示,通过对比发现指数函数拟合精度最高,故将其选为系统的hin(t),如图7所示。

将轴承A的{xshai}作为基本协变量代入式(3),求出C(t)离散形式Ck,对其进行拟合,对比发现指数模型的拟合优度最好,拟合结果如图8所示,其表达式为

C(t)=8.994×105exp(-0.003 964t)

(11)

图6 LRM估计出的初始故障率情况

模型类型模型参数hin(t)=aexp(bt)a=2.35×10-6b=0.003 8hin(t)=atba=7.80×10-27b=7.21hin(t)=aexp(-((t-b)/c)2)a=7.6×10-2b=2.216×103c=3.72×102

表3 不同hin(t)模型的拟合优度比较

图7 初始故障率函数hin(t)及其更新形式

图8 基本协变量函数C(t)及其离散形式Ck

将轴承B的响应协变量指标xsha和协变量函数C(t)代入式(4),对hin(t)进行更新。考虑到响应协变量与故障率间的比例关系假设,将轴承A、B的协变量指数比作为一个乘积因子引入到更新过程当中,因此式(4)改写为

(12)

通过回归分析对其离散形式进行拟合,更新后轴承B的故障率函数h(t)如图7中菱形标记曲线所示,其表达式为

(13)

图9 评估得到的轴承B的可靠度情况

上述轴承可靠性评估实例中只用到了单响应协变量xsha,本节中还提取了其他10个时域指标,每个指标对于轴承故障的敏感性、趋势性、稳定性是不一样的,评估实例中用到的只是一个相对较优的指标。如果能将多个指标进行融合,综合各指标的优势,提取出各方面性能更为出色的新指标,那么评估的效果会更优,如Qiu和Huang在论文中所提出的MQE指标[22],或利用主分量分析、因子分析、距离分析、粗糙集等,先对数据进行降维处理和特征提取,再利用改进的PCM模型进行可靠性估计。

6 结 论

为了完善PCM在少失效数据或零失效数据情况下的工程实用性,本文提出了一种基于改进的PCM可靠性评估方法,通过对航空发动机转子轴承运行可靠性评估应用实例,得出以下结论。

(1)基于LRM的hin(t)估计方法只需要获取设备的响应协变量和对应的状态信息即可,无需对设备的退化失效机理、性能参数的退化路径或概率分布密度函数等做过多的假设。

(2)本文方法绕开了人为确定r和C(t)的过程,避免了主观选择差异带入的估计偏差,从状态监测信号中提取的响应协变量更加准确地揭示设备的时间、动态特性与运行可靠性的映射关系。

(3)对航空发动机转子轴承运行可靠性评估应用实例证明了本文方法的可行性和有效性,为少失效或无失效条件下的运行可靠性评估提供了一种新的手段。