带二维装载约束的车辆调度问题建模及优化
王增臣,周 良
(南京航空航天大学 计算机科学与技术学院,江苏 南京 210016)
0 引 言
物流配送中的车辆调度问题(vehicle scheduling problem,VSP)是由Dantzig和Ramser[1]在1959年提出的,是物流配送中的一个重要步骤,一般可以描述为:对一系列装货点和(或)卸货点,在一定条件(如指定交货时间、车辆载重量、货物的需求量等限制)的约束下,组织适当的车辆路线,达到预定的目的,如行驶时间较少、车辆行驶路程较短、花费成本较少等[2]。
近几十年来,车辆调度问题逐渐成为运筹学和组合优化领域的研究热点,其研究重点也从单因素向多因素协同考虑,各国学者进行了大量和深入的研究工作。马祥丽等[3]针对车辆调度问题,结合蝙蝠算法的原理,重新设计了BA的操作算子并采用罚函数方式对目标函数进行了简化,取得了较好的求解性能。吴聪等[4]将车辆与车辆路径编码成粒子,通过粒子之间的协作找到最优物流配送车辆调度优化方案,并对粒子群算法存在的不足进行了相应的改进,提高了算法性能。Marinakis等[5]提出了一种蜜蜂交配优化算法,并对局部寻优方法进行改进,使算法解决组合优化问题效果更佳,对开放式车辆路径问题也取得了令人满意的结果。Zhang等[6]考虑客户满意度,建立了多目标车辆路径问题模型,提出了一种自适应网格的多目标量子进化算法,利用一种改进的模糊时间窗来反映客户满意程度。邓丽君[7]通过对影响客户满意度的一些影响因素进行分析,构建了一种测度客户满意度的模糊隶属度函数,利用线性加权将多目标函数转化成单目标函数并设计一种改进的遗传算法对单目标函数进行优化求解。以上文献都对车辆调度问题进行研究并取得了一定成果,但在二维装载约束方面研究甚少。刘海明等[8]通过改进最低水平线方法与基于分阶段遗传算子的遗传算法相结合,求解矩形件排样问题,有效改善了排样效果,提高了材料利用率。Sarwono等[9]融合了物流配送中的两个最重要问题,提出了一种最邻近法求解车辆路径问题,并提出了装载启发式算法解决货物装载问题。王征等[10]针对二维装载约束的车辆调度问题建立了数学模型,提出了Memetic算法,对算法中的几个关键算子:深度优先的启发式装箱方法、染色体的编码方式及其路径分割程序等,进行了详细的阐述和改进。
针对近年来实际应用领域中出现的带二维装载约束的车辆调度新问题,文中综合考虑时间窗、二维装载约束、载重量、成本和客户满意度,建立了带时间窗和二维装载约束的开放式车辆路径问题模型(open vehicle routing problem with time windows and two-dimensional loading constraints,2L-OVRPTW),提出了一种结合多目标蚁群优化算法和最低水平线搜索算法的车辆路径优化算法,并通过实验对模型的可解性及算法的有效性进行验证。
1 车辆调度问题建模
1.1 问题描述
2L-OVRPTW问题是融合二维装箱问题(two-dimensional bin packing problem,2BPP)和带时间窗约束的开放式车辆路径问题(open vehicle routing problem with time windows,OVRPTW)之后的一个变种问题[11]。2BPP问题同样属于NP难题,货物能否装载、货物如何摆放等因素都对配送车辆的调度以及服务线路的安排产生很大的影响,因此这两个问题的融合产生了新的问题,有别于一般的车辆路径问题,使得新问题的模型会发生很大的变化,而对新问题进行求解也有较大的挑战[12]。
2L-OVRPTW问题可描述为:一组相同的车辆由配送中心出发,负责给N个客户进行货物配送。每辆车均有一个长为L宽为W的长方形装载空间,且所载货物的总重量不能超过车辆最大载重量Q。每个客户都有随机数量和重量的货物需求,每件货物有特定的长度和宽度[13]。货物装载时,遵守有向有序条件,即同一客户的所有货物必须装载在一辆车上,货物不可旋转,不能相互叠放,并且不同客户的货物之间不能产生阻挡。另外,每个客户都有一个服务时间长度和理想的服务软时间窗[14]。配送中心派送各个车辆并安排行车路线,使得每个客户都能被服务到,每辆车完成任务后不需要返回原配送中心。在这些约束下寻求最佳的车辆调度配送方案[15]。
1.2 2L-OVRPTW模型定义
根据车辆路径问题描述,在建模阶段建立了2L-OVRPTW模型框架,如图1所示。
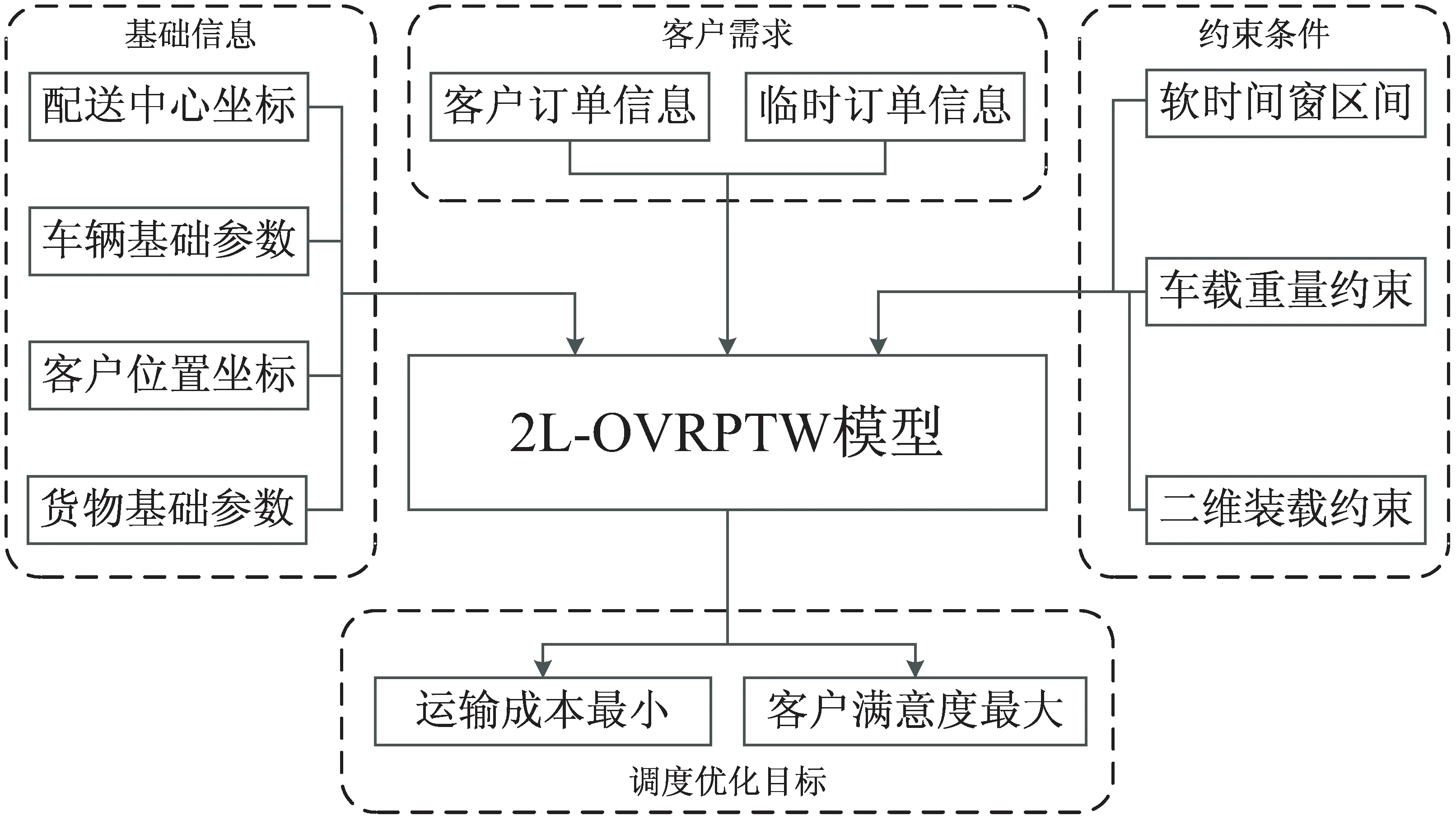
图1 2L-OVRPTW模型框架
2L-OVRPTW模型主要由四个方面组成:基础信息包括客户及配送中心的位置坐标、车辆基础参数和货物基础参数;客户需求是客户的预定订单和临时订单信息;约束条件有软时间窗区间、车辆载重量约束和二维装载约束;调度优化主要是要达到运输成本最小和客户满意度最大的目标。
因此得到模型问题编码:(1)位置:配送中心和客户由N+1个坐标节点表示,0代表配送中心的标号,其他数字表示要被服务的客户标号。标号i到标号j的距离为dij,单位距离的成本为cij。(2)配送中心:有K辆相同的车辆提供运输配送服务,每辆车的额定载重量为Qk(k=1,2,…,K),承载货物的车厢为一个面积A=W×L的矩形,每辆车的固定发车成本为FK。(3)客户:i=1,2,…,N,客户i所需求的货物为一个集合ITi,包含mi个矩形物品,ITi中所有物品的总面积为ai,总重量为qi,第m个物品Iim有一个具体的宽度wim和长度lim(m=1,2,…,mi)。设置车厢承载面俯视图的左下角为原点,水平向右为横坐标,垂直向上为纵坐标,则有物品Iim的坐标(vim,him),vim,him分别代表到坐标原点的水平距离和垂直距离。车辆到达客户进行服务的时间为ti,令每个客户的服务软时间窗为[Ei,Li],客户满意度ui(ti)表示为:
客户i固有的服务时间表示为si,当车辆提前到达客户i处时,则需等待,产生等待时间wi(ti)。等待的单位时间成本为cwait,客户i的等待成本则表示为wi(ti)×cwait。定义决策变量如下:
2L-OVRPTW模型可表示如下:
目标函数为:
(1)
(2)
约束条件为:
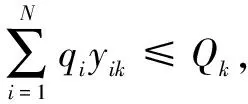
(3)
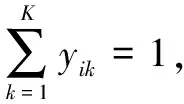
(4)
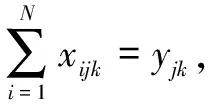
(5)
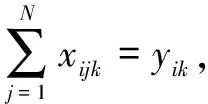
(6)
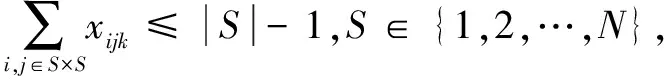
(7)
xijk=0或1,∀i,j,k
(8)
yik=0或1,∀i,k
(9)
0≤vimk≤W-wimk,∀i∈{1,2,…,N},m∈
{1,2,…,mi},k∈K
(10)
0≤himk≤L-limk,∀i∈{1,2,…,N},m∈{1,
2,…,mi},k∈K
(11)
vimk+wimk≤vi'm'k,∀i,i'∈{1,2,…,N},m∈{1,
2,…,mi},m'∈{1,2,…,N},k∈K,i≠i'
(12)
himk+limk≤hi′m′k,∀i,i'∈{1,2,…,N},m∈{1,
2,…,mi},m'∈{1,2,…,N},k∈K,i≠i'
(13)
vimk≥vi′m′k,∀i,i'∈{1,2,…,N},m∈{1,2,…,mi},m'∈{1,2,…,N},k∈K,i≠i'
(14)
himk+limk≥hi'm'k,∀i,i'∈{1,2,…,N},m∈{1,
2,…,mi},m'∈{1,2,…,N},k∈K,i≠i'
(15)
hi'm'k+li'm'k≥himk,∀i,i'∈{1,2,…,N},m∈{1,2,…,mi},m'∈{1,2,…,N},k∈K,i≠i'
(16)
(17)
wi(ti)=max{0,Ei-ti}
(18)
其中,式1~3为目标函数,式1表示运输成本最小化,式2表示平均客户满意度最大化。约束3限制每辆车的最大载重量;约束4保证每个客户都能被服务到;约束5和6保证一个客户有且仅有一辆车进行服务;约束7是消除子回路;约束8、约束9表示变量的取值范围;约束10、约束11保证在每条路径上货物以固定方向都能放置于车上;约束12、约束13表示货物相互之间不可以叠放;约束14~约束16保证货物能在装入方向直线移进移出并不受其他货物阻挡;约束17计算车辆的到达时间;约束18计算车辆的等待时间。
2 车辆调度问题优化
2L-OVRPTW是属于NP-hard难题,启发式算法成为解决该问题的首选[16]。针对上述问题模型,文中设计了一种启发式算法。该算法是以改进的蚁群算法为算法大体框架,并融入了基于BLF的装载策略以确保满足二维装载约束。针对2L-OVRPTW模型设计的调度优化总体流程如图2所示。
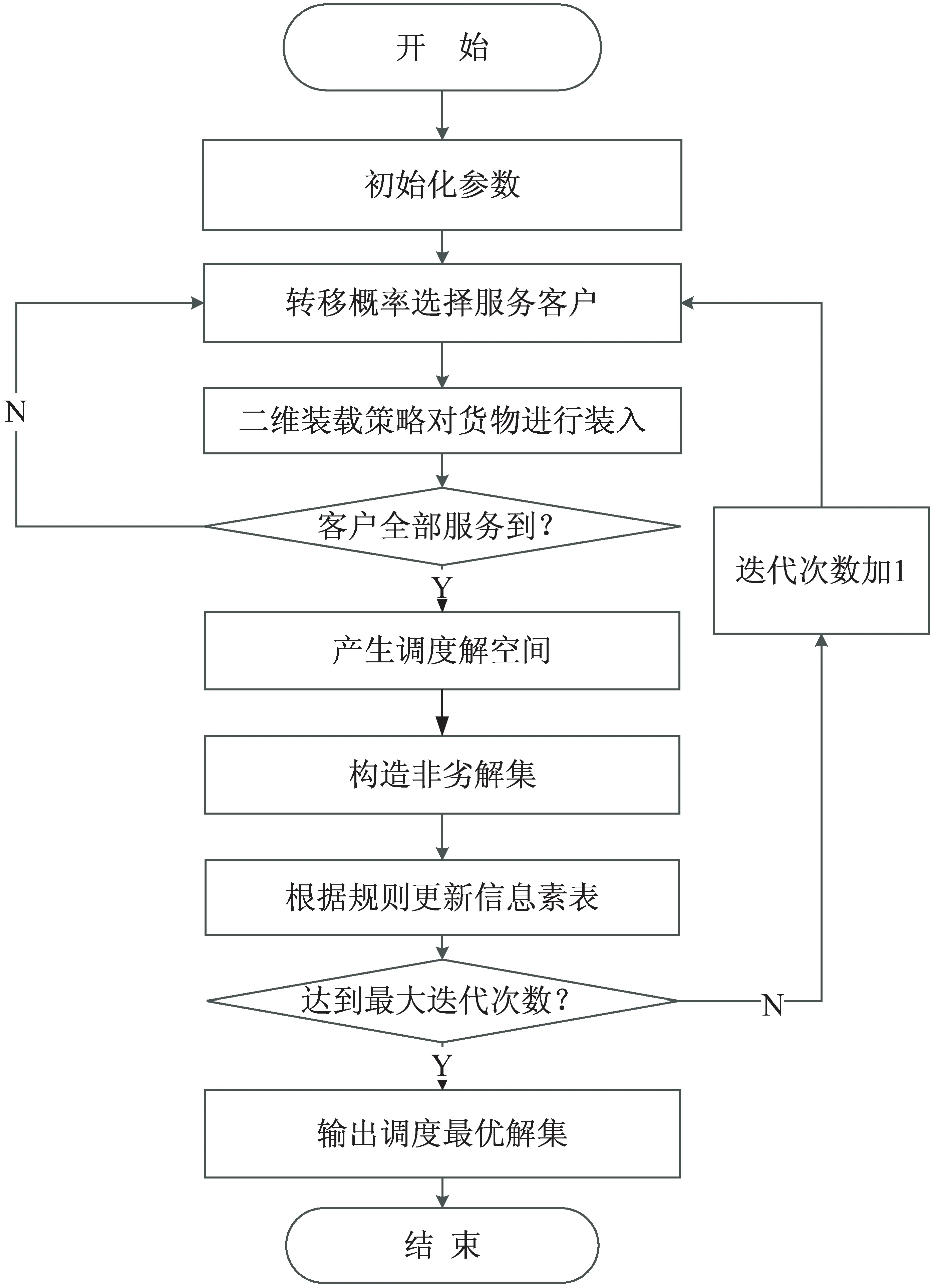
图2 调度优化总体流程
2.1 二维装载策略
在装载阶段,结合启发式经验知识,设计了基于最低水平线搜索算法的二维装载策略,将各个客户的矩形货物有序装入矩形车厢,提高车辆装载率。
2.1.1 启发式经验知识
一般情况下,对于二维装载问题很难直接构造出一个最优解或者满意解,尤其当货物数量比较多时,盲目搜索或者遍历就变得更加困难,甚至根本不可行。因此,利用一些人工经验和结构特征来构造出一些启发式规则,并按照该规则指导采用的启发式算法,由该算法可以求得问题的满意解。
对于二维装载约束,有以下几个经验和特征可以参考利用:
(1)物品装入车厢可行区域的边角处,产生的零碎区域更少,车厢的装载率更高;
(2)先装大块物品,后装小块物品。面积较大的矩形物品装入后产生的区域可以装入面积较小的矩形货品,由人工装箱经验可知,通常先装大块的物品,后装小块的物品;
(3)装载过程中产生的剩余区域整体水平线越平整,即组成水平线的数量越少,高度越一致,就越有利于后期矩形的装入。
基于上述三种启发式经验知识,对现有的最低水平线搜索算法进行指导改进,一个客户的全部物品能且只能由一辆车进行运输服务,在装载之前对该客户货物总面积和车厢剩余面积进行比较;对一个客户的物品按照宽度和面积进行倒序排序,减少不可行区域的产生,同时提高向后搜索匹配的效率;物品放置于可装入的最低水平线的左下方。
2.1.2 装载策略主要步骤
步骤1:将待装载的指定客户i的物品总面积ai与当前车厢剩余面积A剩进行比较:如果ai>A剩,则不可装入,结束;否则对该客户的物品按照宽度和面积进行倒序排序,然后执行步骤2。
步骤2:每当装入客户i的下一待装物品Iim时,比较水平线集中各个水平线高度,选择高度最低的一段水平线,若存在多段水平线段高度相同并且同为最低,则选取位置处于最左边的一段水平线,作为最低水平线Wlow。
步骤3:比较最低水平线段和待装物品Iim的宽度wim:
(1)如果Wlow≥wim,则将Iim放置于最低水平线的左下方,并更新水平线集的条数和高度。
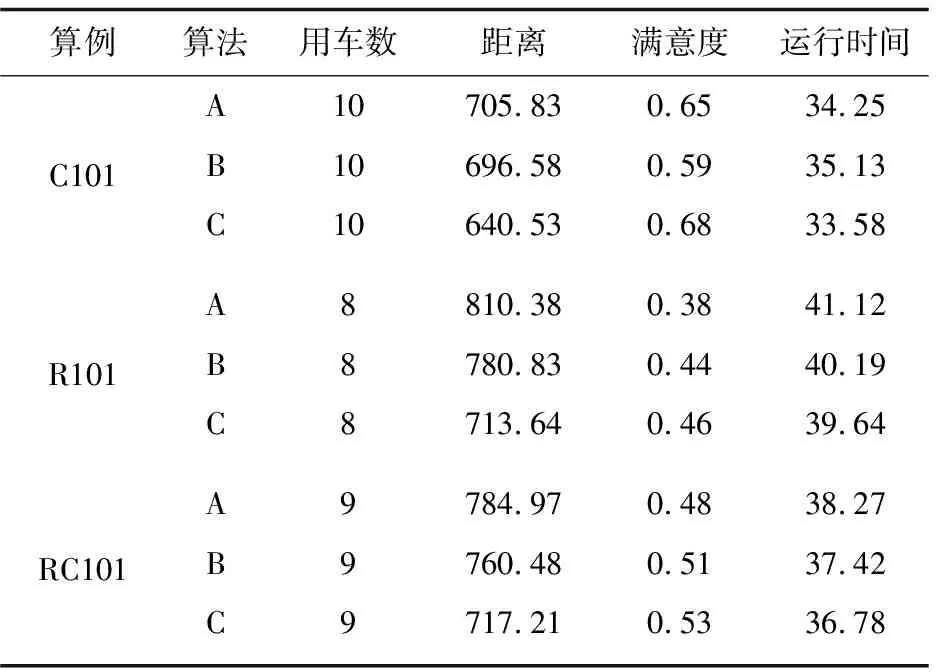
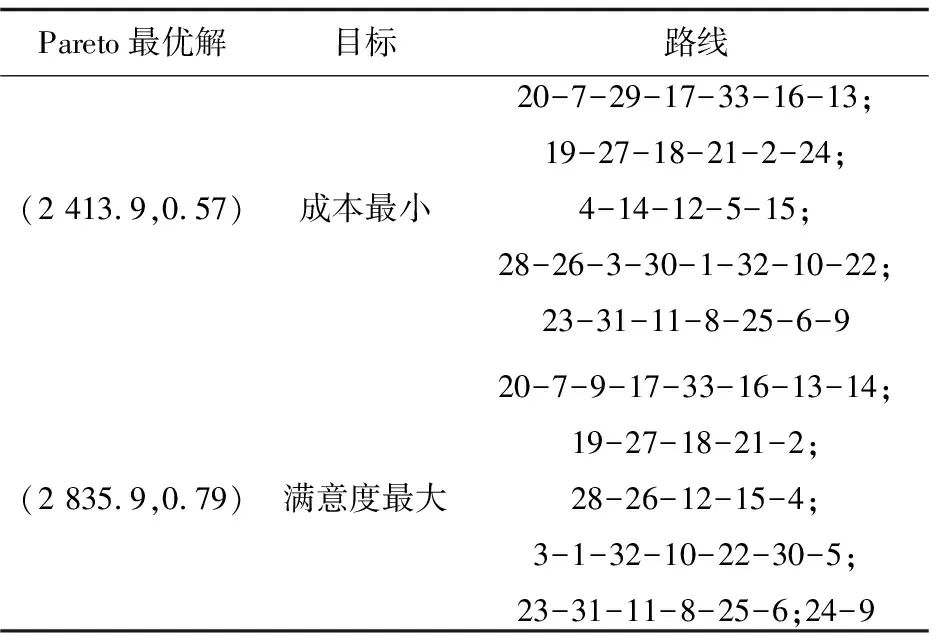
(2)如果Wlow 步骤4:重复步骤3,直至能装入客户i物品Iim,并更新此时的水平线集。 步骤5:重复步骤4,直至客户i的物品全部装入,得到最终的水平线集。 步骤6:选取水平线集中的高度最大值Hmax,与车厢长度L进行比较:如果Hmax>L,客户i的货品不可装入,水平线集更新到客户i的货品未装入前状态,结束;如果Hmax 蚁群算法(ant colony optimization,ACO)是一种新兴的优化技术,是一种模拟进化算法。ACO是一种启发式仿生进化系统,通过模拟蚂蚁群体在自然生活中的觅食行为而得出,其搜索过程是分布式并行计算方式,能够提高算法的计算能力和运行效率,并采用启发式正反馈机制,能够使算法获得全局最优解。 2.2.1 算法的具体改进 由于2L-OVRPTW模型同时优化两个目标,文中设计出多目标蚁群优化算法,在改进的蚁群优化算法基础上,采用Pareto最优解来进行多目标优化[17]。在2L-OVRPTW模型中选择下一客户时,在满足车辆容量和时间窗约束的前提下,还需要考虑时间先后的择优性,其启发式因子由路径距离和客户的时间窗宽度等因素综合决定,因此对状态转移的概率计算和信息素的更新等进行改进。 改进的多目标蚁群算法既可以在迭代运行过程中保持蚂蚁种群的多样性,也能够保持Pareto解集的多样性。 (19) 其中,τij(t)为t时刻客户i或者仓库到客户j路径上的信息素浓度;ηij(t)=1/dij为距离启发式函数;θij(t)=1/twidthj为时间启发式函数。 启发式函数表示t时刻客户i或者仓库到客户j的转移期望程度;allowk为蚂蚁k待访问的客户集合。 在蚂蚁状态转移过程中引入伪随机概率规则,以克服蚂蚁状态转移速度慢的不足,规则如下: j= 其中,r为在[0,1]上服从均匀分布的随机变量;参数r0为用来控制转移规则的概率。若r≤r0,则从待服务的客户中找出概率最大的客户为下一服务客户;否则就根据式19并运用轮盘赌法按概率选择出下一个服务客户。 为了避免路径上的信息素浓度差异过大,引入信息素最低阈值τmin,避免算法过早陷入局部最优。当蚂蚁完成一次循环后,路径上的信息素会挥发,蚂蚁也会留下信息素,需要对各个路径上的信息素进行更新,规则如下: τij(t+1)=max(ρ·τij(t)+Δτij,τmin) (21) (22) (23) 2.2.2 算法主要步骤 步骤1:编码采用整数编码方式并初始化参数。 步骤2:配送中心为蚂蚁的当前起点,将所有客户纳入待服务集合表allow中,清空禁忌表Tabu。 步骤3:蚂蚁在当前位置根据状态转移规则(式20)从集合表allow中选择下一服务客户j,并用二维装载策略对客户j的货品进行装载。 (1)如无法装入或超重,则放弃服务客户j,将蚂蚁位置更新到配送中心,并分配新车辆,转步骤3。 (2)如果装入成功并且不超重,则更新蚂蚁位置到客户j,将客户j从集合表allow转移到禁忌表Tabu中,并重复步骤3直至所有客户全部被服务到。 步骤4:计算种群中每只蚂蚁所走路径的总长度、路线和目标值等信息,并根据各个蚂蚁之间的支配关系构建和更新非劣解集Nset。 步骤5:根据式21~23更新蚂蚁种群的信息素浓度表τ。 步骤6:若迭代次数NC未达到最大迭代次数NCmax,则迭代次数NC=NC+1,并转到步骤2;否则,输出非劣解集Nset,结束。 文中所有程序采用MATLAB编写,在Inter 酷睿 I7-7500U CPU 3.5 GHz、内存4.0 GB的计算机上运行。目前2L-OVRPTW问题尚且没有标准的测试数据库,因此通过对已有的测试实例库进行改造并设计了一个实例来进行算法分析。 为了比较提出的调度优化方法的性能,分别采用遗传算法(A)、混合粒子群算法(B)与提出的调度优化方法(C),对标准Solomon实例库的三个不同类别实例C101、R101和RC101进行改造,多次运行并取平均结果,得到的运行情况如表1所示。通过比较可以看出,用车数量和算法运行时间基本一样,而行驶距离有大幅减少,客户满意度也略有提高。总体而言,文中算法明显优于其他两种算法。 表1 算法比较 将文中算法用于求解某国际物流公司的车辆调度问题的一个实例。在该实例中,物流公司有1个配送中心,为33个客户进行货物配送,每个客户位于不同的坐标上,并有不同种类货物的需求。 在求解过程中,种群大小为50,迭代次数为200,得到Pareto最优解集为(2 413.9,0.57),(2 429.1,0.60),(2 478.3,0.64),(2 544.0,0.72),(2 682.1,0.76),(2 835.9,0.79),如图3所示。分别选取2个目标向量的调度线路,如表2所示。 表2 优化调度线路 一般的车辆调度方法都是满足在客户的需求下,仅从经济因素的角度出发,追求最短的行驶距离或者最低的成本。而在当前激烈的市场竞争环境下,现代物流企业需要综合考虑时间窗、二维装载约束和客户满意度等情况,提高企业竞争力。结合实际情况,文中描述了2L-OVRPTW问题并建立相应模型,以多目标蚁群优化算法为大体框架,并融合改进的最低水平线搜索算法,对模型进行求解,同时优化货物装载和配送路线。实验结果表明,该方法可以在较短的时间内获得模型问题的满意解,满足车辆调度的实时性需求,并具有较高客户满意度和较短的行驶路程。文中设计的模型和车辆调度方法对于现代物流企业科学并合理地开展物流调度工作有一定的理论指导和借鉴意义。2.2 车辆调度优化
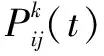
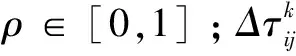
3 实验结果及分析
4 结束语

