基于优化的灰色马尔可夫模型对船舶流的预测

张晓雷，黄洪琼

(上海海事大学 信息工程学院，上海 201306)

0 引 言

近年来，随着社会经济和对外贸易的迅速发展，各种水域的船舶流量也在不断增加，从而导致先进的航行技术和落后的港口运输管理之间的矛盾已经成为现阶段中国水路运输发展的突出矛盾。因此，提升航行水域船舶流量预测的准确性和高效性变得尤为重要[1]。

同时，现实中的多种因素，如季节、气候、经济、地域文化甚至行业的周期性变化等，都会对船舶流量带来直接或间接的影响，所以拥有一种高效、准确的预测模型是十分必要的。

1 理论基础

目前，用于船舶流预测的方法主要包括灰色预测模型[2]、线性回归分析[3]、灰色神经网络[4]、极大似然估计[5]、支持向量机[6]等。这些预测方法具有各自的特点，但有个共同的特点就是要求预测的历史数据有较好的光滑度[7]。故文中采用一种新型的预测方法，即基于季节指数的灰色-马尔可夫预测模型。

在同一年时间内船舶流量的变化存在明显的季节变化，故引入季节指数来对季节变化进行修正。将修正后的数据作为灰色预测模型的原始数据用于建模预测，然后引入Markov模型来修正和弥补灰色模型的预测误差。通过构建实际值与灰色模型预测残差的时间序列，研究误差的变化规律与趋势。

2 模型的建立

2.1 数据的预处理

为了进一步寻找船舶流量在一定时间跨度上的变化规律，在模型中引入功率谱。功率谱即功率密度谱，表征了单位频带内的功率大小，通过功率谱分析可以提取出各个频率分量。以各个月的船舶总流量为采样点，由于一年有12个月，因此采样间隔为12 Hz，得到离散序列{x(n)}。然后，对序列{x(n)}去均值消除零频道影响[8]。同时，采用带阻滤波的方法过滤去1 Hz左右的频率分量，根据滤波后的船舶数据序列功率谱研究确定船舶的年际变化周期。

2.2 季节指数

季节指数是反映事物季节性变动规律的一套指数，表示每年反复出现有规律的周期性变动，且每年上下变动的幅度大体相似。船舶的月流量季节指数可以用来描述一个年度内各个月的船舶流量特征，反映各月的船舶流量占全年的船舶平均数值大小。文中采用平均法[9]测定各月船舶流季节指数，计算步骤如下：

(1)将原始序列{x(n)}按周期分组，划分为N年，每年M=12个数据，即xNM。

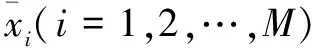
(1)

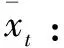
(2)

(4)计算各月季节指数τi：

(3)

(5)测定季节指数后，利用τi对原始数据进行修正。为了满足灰色模型对历史数据的要求，将原始数据进行取对数处理。

2.3 GM(1,1)模型

灰色理论是基于数学理论的系统工程科学，通过少量的、不完全的信息，建立灰色微分预测模型[10]，故可以运用灰色理论的方法解决船舶流的预测问题，而GM(1,1)模型是最常用的灰色模型。

设经过季节指数修正和对数变换后的数据列为：

x(0)={x(0)(1),x(0)(2),…,x(0)(n)}

(4)

其中，n为序列长度。

将式4进行累加，得：

x(1)={x(1)(1),x(1)(2),…,x(1)(n)}

(5)

其中：

(6)

(7)

其中，α为参数，记为A=[ab]T，并用最小二乘法确定参数：

A=(BTB)(-1)BTXN-1=[ab]T

(8)

其中：

(9)

xN-1=[x(0)(2)x(0)(3)…x(0)(n)](T)

(10)

得到微分方程：

(11)

经过累减还原得到：

(12)

模型误差分析时，常用相对误差进行检验，即：

(13)

平均相对误差为：

(14)

2.4 马尔可夫修正模型

灰色预测依旧存在一定误差[12]，故引入马尔可夫模型进行修正。马尔可夫模型的预测原理是根据某些变量的显著状态及其变化趋势，预测其在未来某一特定期间内可能出现的状态[13]，步骤为：

(1)计算波动指数序列：由式13可得δk。

(2)划分Markov状态。

δk∈[α1i,α2i],i=1,2,…,s

(15)

上式表示第k对象的波动指数处于第i种状态Ei，α1i、α2i分别表示Ei的上、下界。因此，总的状态集合表示为E=(E1,E2,…,En)。

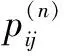
(16)

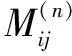
(4)构造未来状态矩阵pij。

根据相对于预测目标的距离选取s个预测对象，按照从近到远的顺序排序，分别以各个对象所对应的状态为矩阵的初始状态，在n步转移概率矩阵p中选取各自所对应的行向量[14]，构造出新的概率矩阵：

(17)

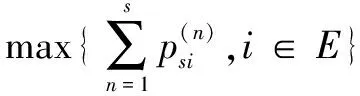
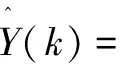
k=1,2,…,n

(18)

3 实验仿真及结果分析

以MATLAB为实验平台，测试数据选取武汉大桥断面2007年1月—2016年12月的船舶交通流量，其中以2007年1月—2015年12月的108个数据作为学习样本来建立模型，以2016年12个月的船舶流量数据作为测试样本来检测模型。模型原始数据x(0)为：

(19)

2007年—2015年的船舶交通流量数据序列经过过滤以后的功率谱如图1所示。

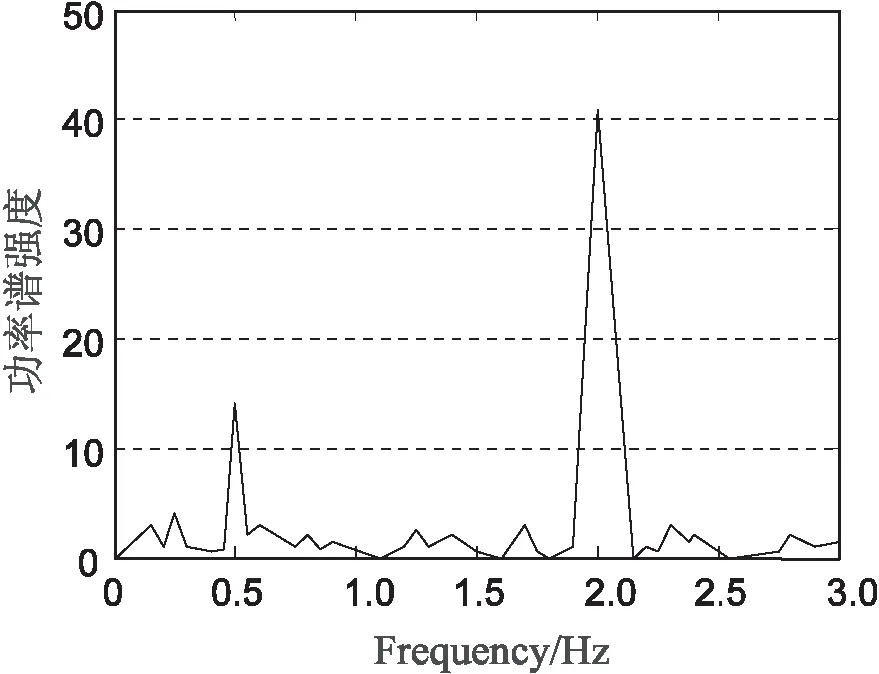
图1 滤去1 Hz分量后的月船舶流量功率谱

由图1可知，功率谱中有2个比较明显的峰值：

(1)频率为2 Hz时，对应0.5年的周期分量，其功率谱强度和一年中季节和生活规律的升降规律一致；

(2)频率为0.5 Hz时，对应2年的周期分量，表明船舶流的年际变化以2年为周期，因此，文中确定武汉大桥的船舶流量的季节性变化周期为2年。

综上，用GM(1,1)预测模型进行逐年预测，得出了2007年—2015年各月船舶流量的误差计算结果，如表1所示。

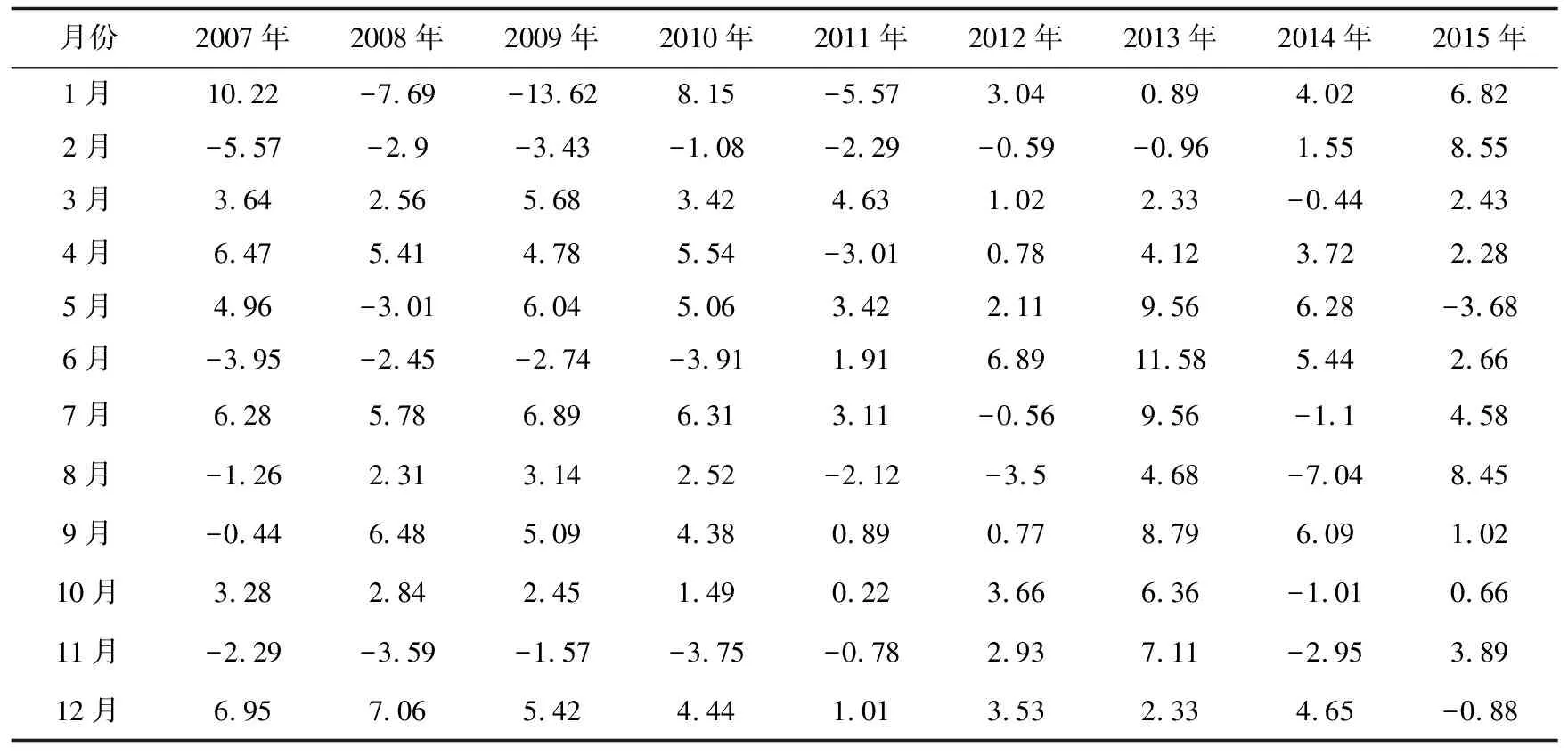
表1 2007年—2015年各月的船舶误差表

通过用上述方法对数据进行处理后，分别用GM(1,1)模型和马氏修正后的GM(1,1)模型对2016年各个月的船舶流进行预测，并与实际值进行对比。同时，为了更好地对实验结果进行对比，用BP神经网络[15]对同一时间段的船舶流量进行了预测，结果分别如图2～4所示。

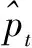
(20)

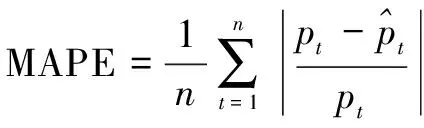
(21)

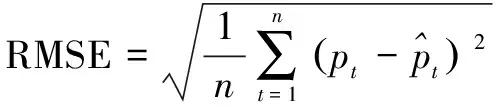
(22)

将三种模型的MAE、MAPE、RMSE进行计算比较，其结果如表2所示。

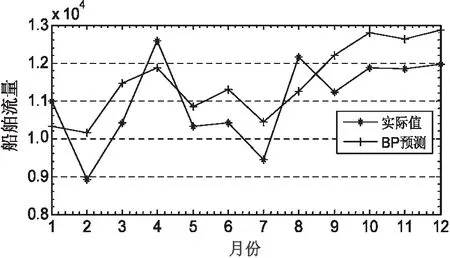
图2 BP神经网络模型预测结果

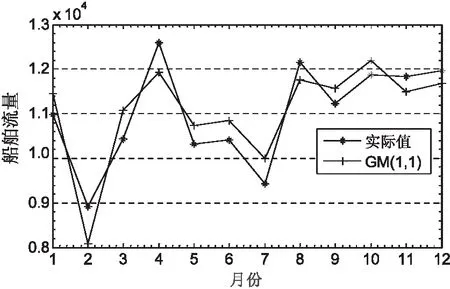
图3 GM(1,1)模型预测结果

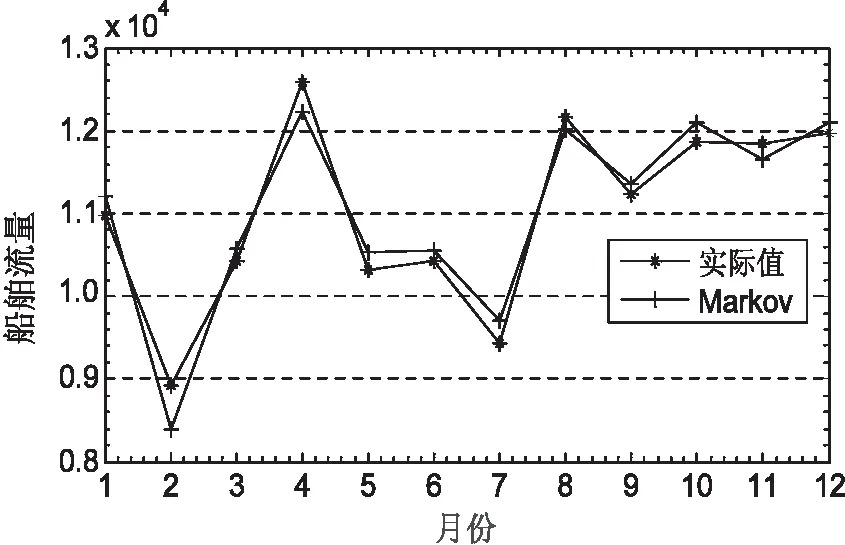
图4 马氏修正后的预测结果

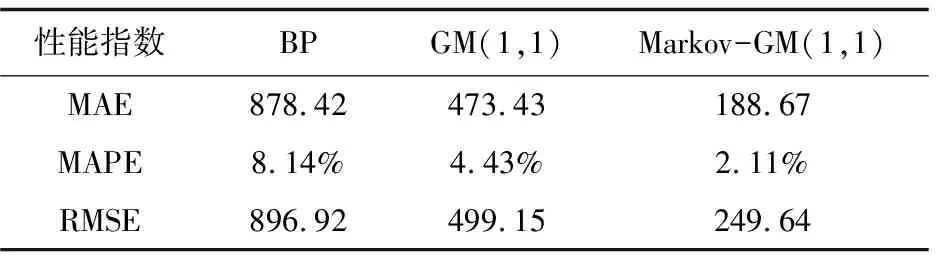
性能指数BPGM(1,1)Markov-GM(1,1)MAE878.42473.43188.67MAPE8.14%4.43%2.11%RMSE896.92499.15249.64

由表2可知，Markov-GM(1,1)预测模型的MAE、MAPE、RMSE都明显小于BP模型和GM(1,1)模型。因此，Markov-GM(1,1)模型比BP神经网络模型和GM(1,1)模型在船舶预测的准确性和高效性等方面优势显著。

4 结束语

在实际生活中，船舶交通流量会受到季节、气候、人为活动等因素的影响而形成季节性周期波动。文中利用周期波动性因素，在传统灰色预测模型的基础上，引入马尔可夫模型对其进行修正，构建了一种新型的船舶预测模型。实验结果表明，改进的预测模型可以更好地反映出船舶流量的总体变化趋势和数据波动特征，并且与传统的预测模型相比，Markov-GM(1,1)模型的预测精度更高，稳定性更好。研究表明，该方法适用于中长期船舶交通流量的预测。