柔性制造系统的部分可观时间Petri网故障诊断

张治国，刘久富，郑 锐

(南京航空航天大学 自动化学院，江苏 南京 210016)

0 引 言

柔性制造系统(flexible manufacturing system，FMS)通常由多个单元构成，各单元相互配合完成复杂加工任务。成熟的柔性制造系统动态行为更加复杂，可在24小时无人操作下智能生产，极大减少工人工作量，满足企业对市场需求的应变[1-3]。柔性制造系统在制造业的优势越来越明显，但实际生产过程中，也存在制造复杂，运行模式多样化等导致故障频繁，故障样本难以获取，关键设备无法及时检测运行状况等问题[4-6]。因此，对柔性制造系统的故障诊断研究势在必行。

目前国内外很多科研机构都在开展关于柔性制造系统的故障诊断方法研究，并取得了一定成果。北京理工大学等机构在机器人可靠性分析研究时引入了故障树的研究方法，通过故障树定性定量的分析针对单一设备的故障诊断有了一定的理论实践研究[7]。Kuo等从FMS运行过程的行为角度出发,使用有色Petri网建模实现对FMS的状态监测及故障诊断[8-9]。

针对柔性制造系统，以往基于定性模型的故障方法已经取得了丰硕的成果，但主要集中在可观节点的故障诊断，对不可观节点的故障诊断还不够完善。对此，文中提出一种基于部分可观时间Petri网的故障诊断方法，把部分可观时间Petri网[10-12]和状态类图(state class graph，SCG)[13-14]相结合，构建修正状态类图(modified state class graph，MSCG)，把复杂的并行事件转变成求解满足时间约束的序列集合。所有节点分为可观节点和不可观节点，根据各节点变迁触发时间范围和可观节点触发时间信息，结合提出的故障诊断方法，判断系统不可观节点是否发生故障。

1 部分可观时间Petri网的故障检测问题

1.1 部分可观时间Petri网

定义1：Petri网(Petri nets，PN)定义为N=(P,T,Pre,Post)，其中P为库所(place)集合，T为变迁(transition)集合，Pre:P×T→和Post:P×T→分别是输入弧和输出弧的集合，每个库所的资源个数为M(p)。

定义2：时间Petri网(time Petri nets，TPN)定义为Nd=(N,Q),N=(P,T,Pre,Post)是Petri网的四元数组，Q:T→×(∪{∞})是系统初始状态下变迁时间约束条件，Q(ti)=(li,ui)，li≥0,ui≥li，li和ui均为自然数。

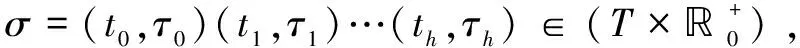
定义3：标签Petri网(label Petri net，LPN)定义为，L:T→L∪{ε}为每个变迁分配一个标签L或空符号ε，分别对应可观变迁和不可观变迁。

1.2 故障检测问题

(1)

定义5：给定一个时间标签序列集合

和一个时间τ≥τl(δ0)，对应的标识集合为：

C(δ0,τ)={M∈m|M0[σ〉M,σ∈∑(δ0,τ)}

(2)

定义6：给定一个时间标签序列集合

和一个时间τ≥tl(δ0)，对应的状态集合为:

S(δ0,τ)={Mk,Θk|Mk∈C(δ0,τ),Θk={lki≤θki≤uki}},lki≥0，uki≥0

(3)

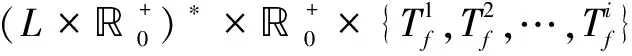
记log(σ)为去掉时刻τ的变迁序列集合。

2 基于MSCG图和时间Petri网的故障诊断方法

2.1 修正状态类图构建方法

在状态类图方法[12-13]的基础上添加时间变量和时间约束,构建基于标签时间Petri网的修正状态类图。

算法1：构建MSCT。

输入：TPN系统

输出：修正状态类树(MSCT)

1．初始化 节点C0对应标识

根节点标记B(C)=E

while 存在一个标记B(C)=E的节点do{

2．节点标识为Ck，B(C)=D

3．for ∀ti∈A(Mk) do{

5．ti在标识Mk触发，Mq=Mk+C(·,ti)

6．for ∀tr∈A(Mq)do{

iftr∈A(Mk)且Mk-Pre(:,ti)≥pre(:,tr) pre(:,tr) then

7．建立新节点Cq标识为Mq,约束集合为：

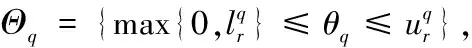
if存在和Cq相同节点 then

Cq节点标记B(C)=D

ElseCq节点标记B(C)=E}}}

在MSCT中复制标记为B(C)=Z的节点，构建MSCG图。

2.2 基于MSCG图和时间Petri网的状态估计

π=Cq0(Mq0,Θq0),ti1,L(ti1)

Cq1(Mq1,Θq1),ti2,L(ti2)

……

Cq(k-1)(Mq(k-1),Θq(k-1)),tik,L(ti(k-1))

Cqk

(4)

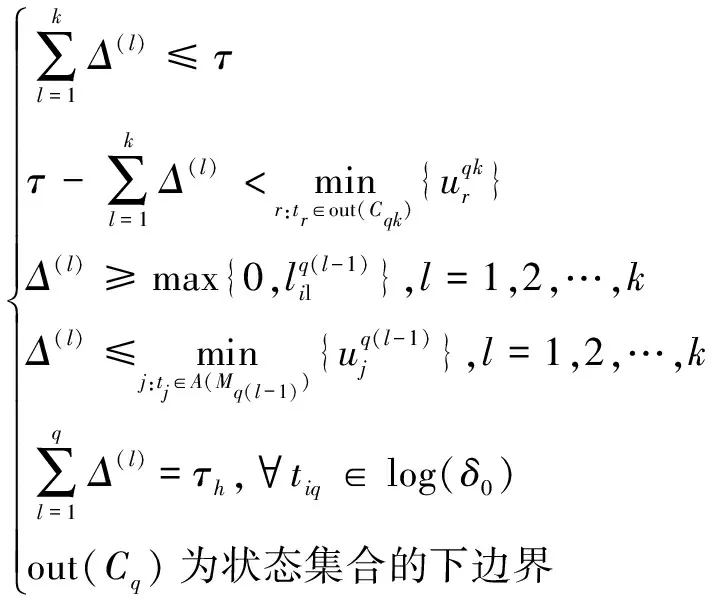
(5)

给定路径π，定义obs(π)为其对应的可观序列，式(5)中obs(π)=L(ti1,ti2,…,tik)。

步骤16判断系统是否发生故障。任意π∈Ⅱ，都不存在tf∈π，系统没有故障；存在π∈Ⅱ，满足tf∈π同时存在π'∈Ⅱ满足tf∉π'，无法判断系统是否故障；所有π∈Ⅱ都满足tf∈π，系统故障。

算法2：基于MSCG的状态估计与诊断算法。

输入：TPN系统及对应MSCG图，TLS集合δo=(γi1,τ1)…(γih,τh)，时间τ

1.初始化:δ0=ε,S(δ0,0)=∅

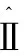
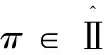
4.for 所有π∈Ⅱ路径 do{

S(ε,0)=S(ε,0)∪{(M,Θ)}，(M,Θ)是路径π最后节点}

5.if 给定S(ε,τ)，τ>0 then{

7.for所有π∈Ⅱτdo

S(ε,τ)=S(ε,τ)∪{(M,Θ′)},Θ′是根据式5得出的最后节点时间约束}

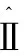
12.forπ∈Ⅱ do{

S(δ0,τ)=S(δ0,τ)∪{(M,Θ)} }

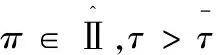
15.for所有π∈Ⅱτdo

S(δ0,τ)=S(δ0,τ)∪{(M,Θ′)} }

16.fori=1,2,…,rdo{

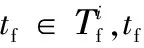
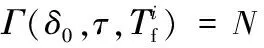
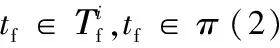
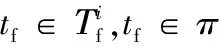
3 实例分析与验证

某柔性制造系统(FMS)由一台加工中心M和多台数控机床组成，并行生产一组零件。工序设计要求工件b根据工件a在M的校刀数据进行加工。

3.1 构建柔性制造系统模型

图1以柔性制造系统加工过程中关键节点为库所，关键动作为变迁建立Petri网模型，模拟柔性制造系统加工过程，各库所、变迁含义如表1、表2所示。

图1 柔性制造系统Petri网模型

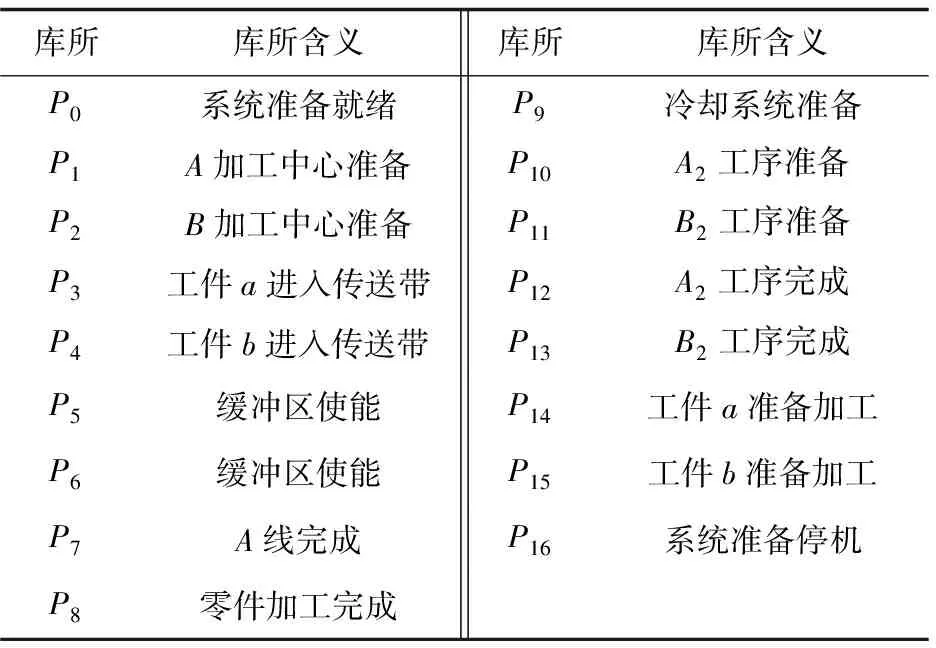
库所库所含义库所库所含义P0系统准备就绪P9冷却系统准备P1A加工中心准备P10A2工序准备P2B加工中心准备P11B2工序准备P3工件a进入传送带P12A2工序完成P4工件b进入传送带P13B2工序完成P5缓冲区使能P14工件a准备加工P6缓冲区使能P15工件b准备加工P7A线完成P16系统准备停机P8零件加工完成

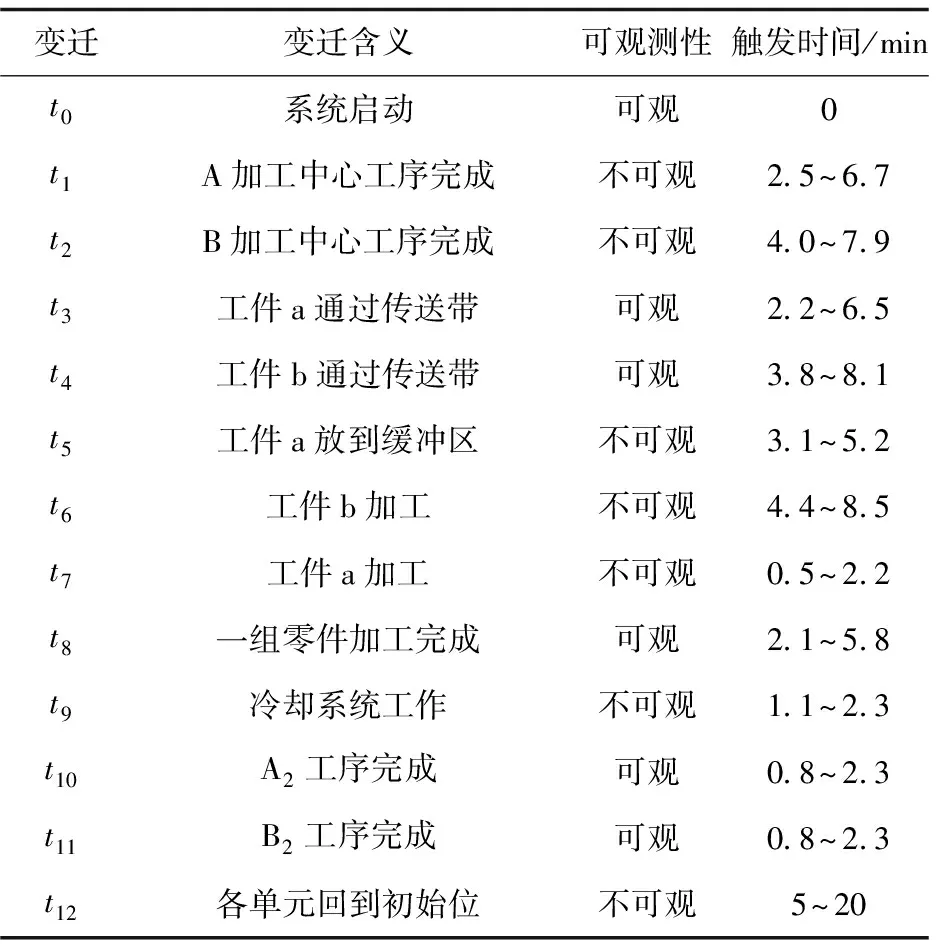
表2 图1中各变迁物理含义、可观测性及设计动作时间

该柔性制造系统工作流程为[15-16]：毛坯a，b分别进入A，B支路，经过数控机床相应工序变成工件a，b；工件a先进入加工中心M校准刀具加工，工件b再进入加工中心M根据工件a的校刀数据加工。最后完成一组零件的加工。

3.2 柔性制造系统故障诊断

3.2.1 构建柔性制造系统的MSCG图

根据算法1构建MSCG图，标识M及时间约束Θ构成每个节点的基本信息，所有可能路径为{t0t1t2t3t4t10t11t5t7t6t8,t0t1t2t3t4t11t10t5t7t6t8,t0t1t2t3t10t4t11t5t7t6t8,t0t1t2t4t3t10t11t5t7t6t8,t0t1t2t4t3t11t10t5t7t6t8,t0t1t2t4t11t3t10t5t7t6t8}等。

图2 节点C1C2C3对应的MSCG图

以{t0t1t2t3t4t10t11t5t7t6t8}为例简述修正状态类图构建过程，图2是变迁t0t1触发对应节点C1C2C3的MSCG图。标识M0和时间约束Θ0构成初始节点C0对应的使能变迁为t0；节点C1由变迁t0在C0触发得到，标识M1[011000000010000000]对应的使能变迁为t1,t2，且Q(t1)=[2.5,6.7]，Q(t2)=[4.0,7.9]；节点C2由变迁t1在C1触发得到，标识M2[001100000010000000]对应的使能变迁为t2,t3，变迁t2能触发需满足Δ1≤min{u1,u2}，所以修正后的Q(t2)=[4.0-Δ1,7.9-Δ1]；节点C3由变迁t2在C2触发得到，标识M3[000110000010000000]，对应的使能变迁为t3,t4，变迁t3能触发需满足Δ2≤min{u2,u3}，所以修正后的Q(t3)=[2.2-Δ2,6.5-Δ2]，同理构建其他节点。

3.2.2 基于MSCG图柔性制造系统的故障诊断结果

柔性制造系统中工业机器人腰部回转故障影响系统正常工作。文中Petri网模型中，工业机器人腰部回转无故障情况下，工件a放到缓冲区(变迁t5)会在A2工序在3.1～5.2 min内完成，若工业机器人腰部回转故障便会导致变迁t5完成的时间推迟到5.2～12.3 min内。图3是根据仿真数据及文中算法进行故障诊断的结果，其中τ是采集有效数据的时间上限。

由图3可知，在第一次实验中，可观序列(t0,0)(t3,7.6)(t10,8.6)(t4,11.7)(t11,13.1)触发后，由算法2计算所有能够触发的变迁序列σ，其中正常变迁4条，故障变迁0条，系统诊断结果为无故障。可观序列(t8,24.9)触发后，由算法2计算所有能够触发的变迁序列σ，其中正常变迁4条，故障变迁2条，系统诊断结果为可能故障。

δ0/minτ/minTiflog(σ)Γ(δ0,τ,Tif)第一次实验(t0,0)(t3,7.6)15.5t5{t0t1t2t3,t0t2t1t3}N(t0,0)(t3,7.6)(t10,8.6)16.0t5{t0t1t2t3t10,t0t2t1t3t10}N(t0,0)(t3,7.6)(t10,8.6)(t4,11.7)18.3t5{t0t1t2t3t10t4,t0t2t1t3t10t4}N(t0,0)(t3,7.6)(t10,8.6)(t4,11.7)(t11,13.1)44.3t5{t0t1t2t3t10t4t11,t0t2t1t3t10t4t11,t0t1t2t3t10t4t5t11,t0t2t1t3t10t4t5t11}N(t0,0)(t3,7.6)(t10,8.6)(t4,11.7)(t11,13.1)(t8,24.9)64.3t5{t0t1t2t3t10t4t11t5t7t6t8,t0t2t1t3t10t4t11t5t7t6t8,t0t1t2t3t10t4t5t11t7t6t8,t0t2t1t3t10t4t5t11t7t6t8,t0t1t2t3t10t4t11tft7t6t8,t0t2t1t3t10t4t11tft7t6t8}U第二次实验(t0,0)(t3,7.3)15.5t5{t0t1t2t3,t0t2t1t3}N(t0,0)(t3,7.3)(t4,8.3)15.5t5{t0t1t2t3t4,t0t2t1t3t4}N(t0,0)(t3,7.3)(t4,8.3)(t10,8.5)18.3t5{t0t1t2t3t4t10,t0t2t1t3t4t10}N(t0,0)(t3,7.3)(t4,8.3)(t10,8.5)(t11,9.8)44.3t5{t0t1t2t3t4t10t11,t0t2t1t3t4t10t11}N(t0,0)(t3,7.3)(t4,8.3)(t10,8.5)(t11,9.8)(t8,31.2)64.3t5{t0t1t2t3t4t10t11tft7t6t8,t0t2t1t3t4t10t11tft7t6t8}F

图3 柔性制造系统故障诊断结果

第二次实验中，可观序列(t0,0)(t3,7.3)(t4,8.3)(t10,8.5)(t11,9.8)触发后，由算法2计算所有能够触发的变迁序列σ，其中正常变迁2条，故障变迁0条，系统诊断结果为无故障。可观序列(t8,31.2)触发后，由算法2计算所有能够触发的变迁序列σ，其中正常变迁0条，故障变迁2条，系统诊断结果为故障。

4 结束语

针对Petri网模型中不可观节点故障诊断问题，提出一种构建修正状态类图的故障诊断方法，由算法2计算MSCG图中所有满足可观序列集合S(δ0,τ)的序列σ并诊断系统是否发生故障；建立柔性制造系统的部分可观时间Petri网故障诊断模型，根据变迁之间触发关系修正各自对应的时间约束，由算法1构建对应的修正状态类图(MSCG),再根据算法2诊断系统的故障状态。仿真结果表明，该算法能够满足实际应用要求。

未来将研究标签时间Petri网的可诊断性，系统结构和变迁数目影响构建MSCG图的计算复杂度，当系统变迁数目过多时，该算法还需进一步改进。