基于Redis单位最大效益自适应迁移策略研究
韦 立,陈珊珊
(1.南京邮电大学 计算机学院,江苏 南京 210003;2.江苏省大数据安全与智能处理重点实验室,江苏 南京 210003)
1 概 述
为了应对海量数据带来的挑战和解决传统数据库访问大规模数据的瓶颈问题,NoSQL[1]型数据库应运而生。以MongoDB[2]、Redis[3]、Cassandra[4]为代表的NoSQL产品以其高性能、强扩展性和高容错性受到了人们的青睐,并在数据库领域掀起了一场新的革命。NoSQL数据库常常以Key-Value形式存储,Key-Value存储技术为应用提供低延时、高可用、可伸缩的数据访问服务。对于Key-Value存储系统,数据迁移[5]是实现节点动态扩展与弹性负载均衡[6]的关键技术,而Key-Value常用的数据分布策略是一致哈希。一致性哈希可以达到很好的分布式均匀性,并且由于特殊的放置规则,其在节点数据发生变动时可以将影响控制在局部区间内,从而保证非常少的数据迁移。当然,必要的迁移代价必不可少,因此如何有效降低迁移代价、提高迁移效益[7]是Key-Value存储需着力解决的问题。
Redis从3.0版本开始支持集群功能,集群采用无中心节点方式,实现客户端直接与Redis集群的每个节点连接,节点之间通过Gossip协议交换互相的状态和探测节点扩展、删除信息(见图1)。Redis集群中有一个长度为16 384的哈希槽,这个槽是虚拟的,并不是真正存在的。正常工作时,Redis集群中的每个节点都会负责一部分的槽,当有某个Key被映射到某个主节点负责的槽,那么这个主节点负责为这个Key提供服务,至于哪个主节点负责哪个槽,可以由用户指定,也可以在初始化时自动生成。所以,当集群添加节点时,用户可以从其他节点随机各抽取一部分槽到新节点,也可以指定某些节点上的槽迁移到新节点。但是目前Redis集群数据迁移操作必须手动进行,而且随机选择的迁移方案也并不是最优的。为了实现数据有策略的迁移,文中提出了单位最大效益自适应迁移策略。
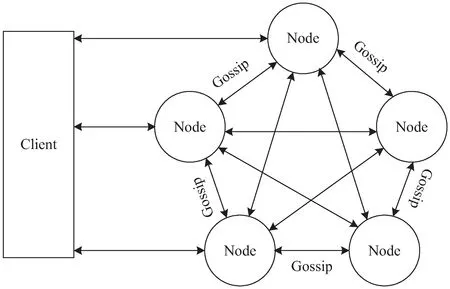
图1 Redis集群无中心节点模式
秦秀磊等[8]提出基于面积的迁移代价模型和开销敏感迁移算法来完善Key-Value迁移机制。他们用二维空间面积衡量迁移节点之间的迁移代价,任意的迁移代价可用对应的矩形面积来表示,因此将迁移代价选择转为矩形面积的选择。开销敏感迁移算法基于迁移代价模型,算法每次选择代价最小的节点进行迁移,这样选取的迁移策略确实减少了迁移代价,然而开销敏感迁移算法并没有考虑数据量的问题,因此选取的迁移方案并不是最优的。通过分析开销敏感迁移算法存在的不足,文中基于面积迁移代价模型,提出的单位最大效益自适应迁移策略包含两部分:负载自适应平衡策略和单位最大效益迁移方案。负载自适应平衡策略通过实时判断集群系统负载情况解决Redis手动迁移的不足,有策略的数据迁移使其静态存储均衡化,从而实现系统之间的自适应调控;单位最大效益迁移方案每次优先选择单位效益最大的节点进行迁移,直至迁移完成。单位最大效益自适应迁移策略主要实现三个过程:数据迁移时机的选择,即在什么情况下触发迁移;迁出节点和迁入节点的选择,即迁出节点和迁入节点的判定;迁移效益的选取,即选取效益最大的迁移方案。
2 单位最大效益自适应迁移策略
2.1 系统负载
对于负载均衡的考虑,模型引入信息熵[9]的概念来衡量集群的负载。假设节点i的负载水平为li,标准化节点负载Pi见式1,平均负载见式2:
(1)
(2)
集群所需要的是节点负载的均匀程度,信息熵完全可以作为系统有序化和均匀程度的一个度量。因此,自适应迁移策略采用信息熵表示集群的负载分布情况,如式3:
(3)
熵值越高,表明负载分布越均匀。当各节点负载相等时,系统取得最大熵值H(P)max=logn。
为了更加直观地表示负载分布情况,自适应迁移策略还构建了一个均衡度函数F∈(0,1),即标准化熵值,见式4:
(4)
2.2 自适应平衡策略
为了实现Redis数据有策略的迁移,使其静态存储均衡化和负载均衡,构建了一个负载均衡的自适应的数据迁移框架,如图2所示。
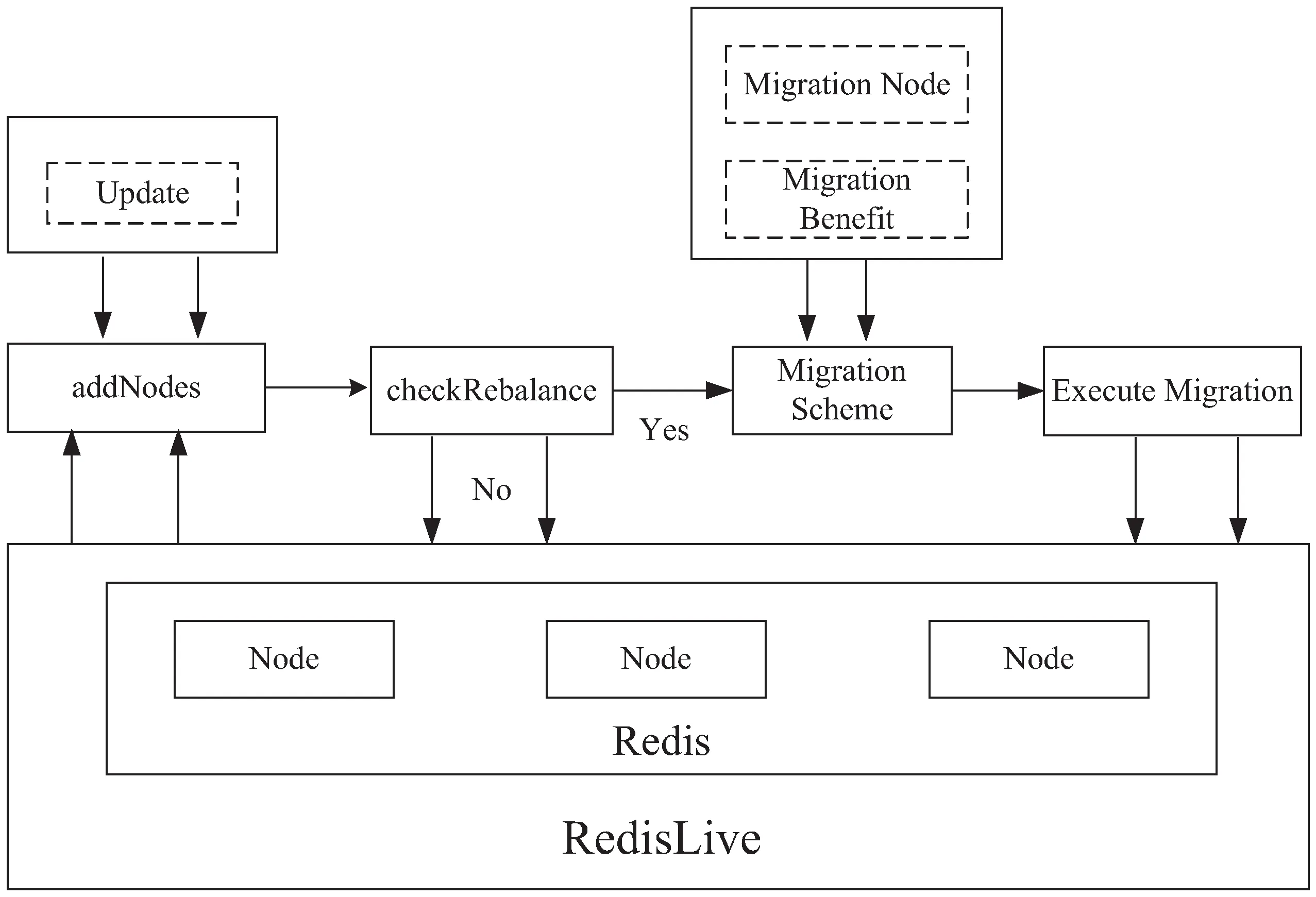
图2 自适应负载平衡框架
数据信息通过哈希算法[10]将数据分布在各个虚拟节点实现数据的均匀分布;当数据更新时,RedisLive对集群进行实时监测并收集信息。如果整个系统的负载低于均衡度阈值就会触发数据迁移操作,反之,仍然保持当前状态;迁移方案的选择尤为关键,迁出迁入节点的选择和迁移代价的比较等因素都是衡量的重点,统筹这些因素,制定出迁移最大效益的方案;最后,执行数据迁移。
Redis集群通过哈希算法将数据分布在各个虚拟节点实现数据的均匀分布,因此数据可以维持数据平衡。然而,当Redis集群为实现横向扩展而增加新节点时,平衡策略自适应地将进行有策略的数据迁移。算法1主要包含三个步骤:判断、挑选、迁移。
Algorithm1:The checkRebalance procedure
procedure checkRebalance(add or remove nodes)
calculateF
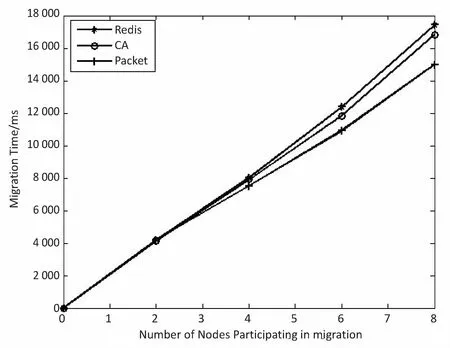
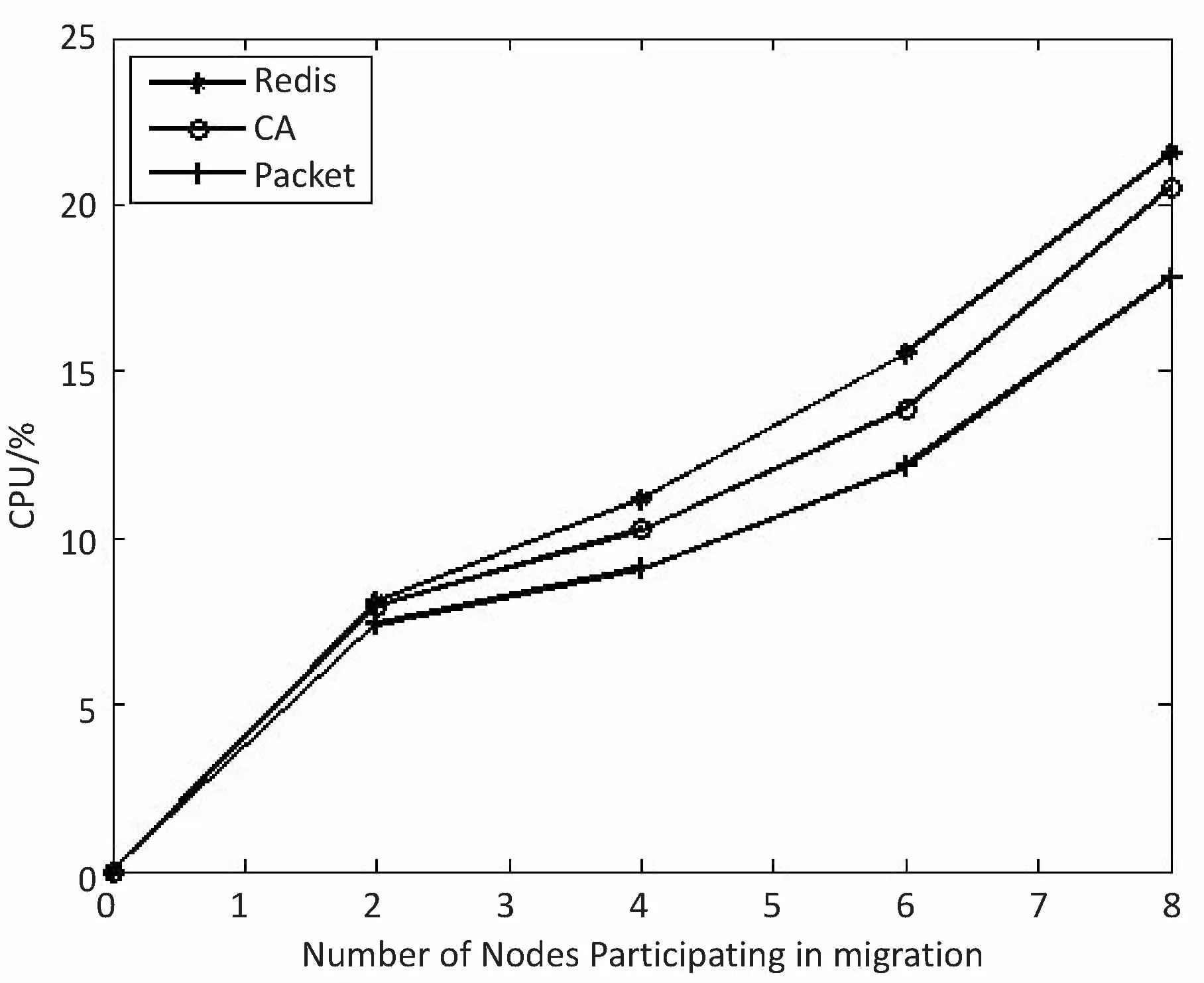
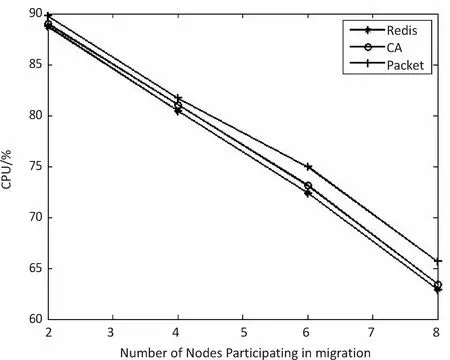
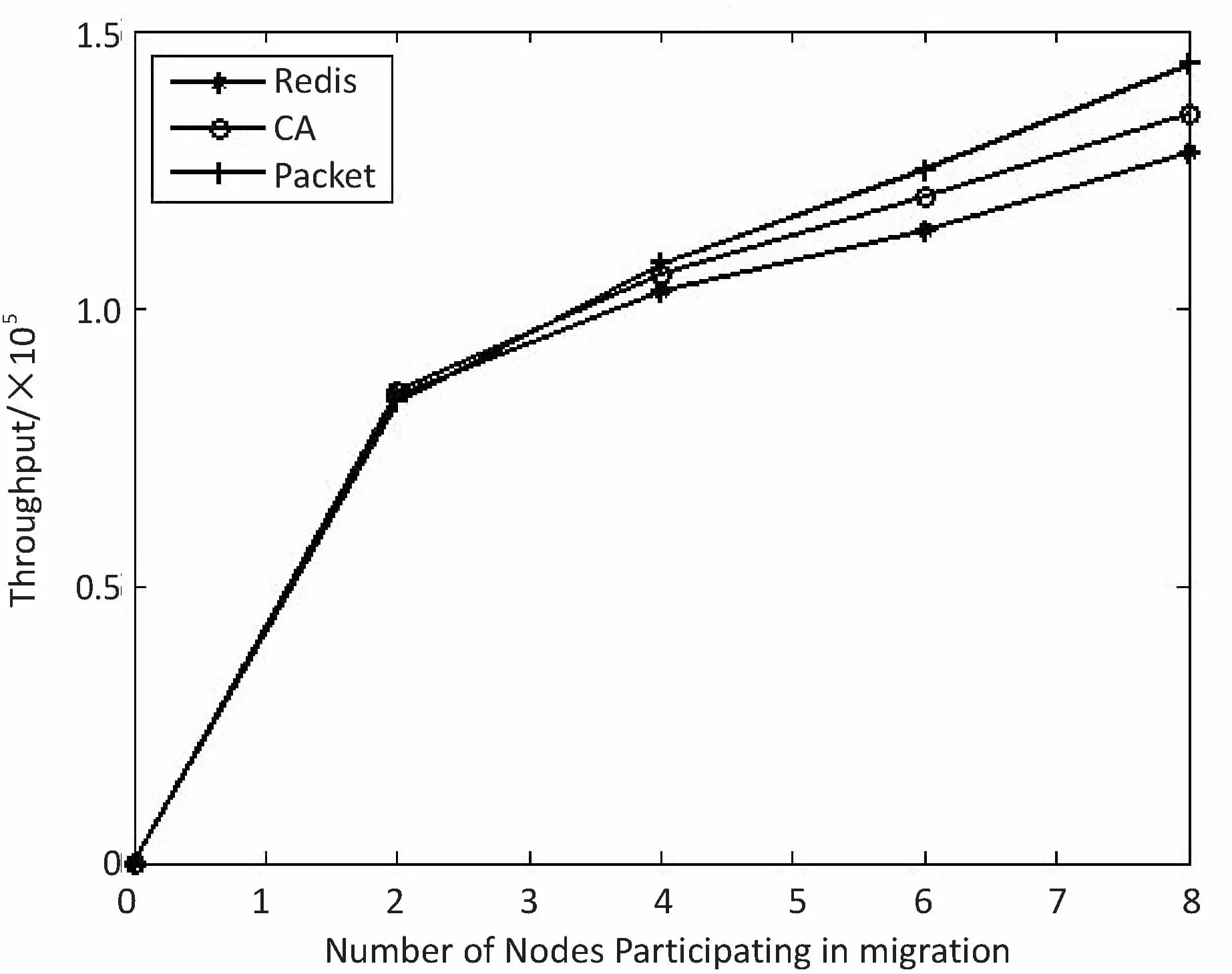
ifF engage(nodes) do migrationS return Else return End 判断:通过信息熵计算方法,集群计算出当前系统的均衡度函数,并预先设定一个阈值。开始阶段整个集群系统比较稳定,但是随着新节点的添加,当前负载平衡系统被打破,触发节点进行数据迁移,这也是对应了迁移时机的考虑。当F小于阈值,CheckRebalance算法触发数据迁移操作,自适应调节节点存储情况。 选取:一般来说,数据迁移操作不会选择整体节点进行操作,这样做目标繁多,而且带来的开销也很巨大。因此,文中有目的性地选择一些需要参加的节点进行数据迁移操作,以大大减少迁移代价。根据信息熵,每个节点i都会有各自的节点负载li和平均负载lavg。于是,所有参加操作的节点分成两类,分别是迁入节点和迁出节点。当节点i的负载水平li 迁移:上面已经确定迁移时机,并选取部分参加的节点进行迁移操作,接着就是选择最大效益迁移方案。Redis集群数据迁移随机选择节点进行数据迁入或者需要手动迁移槽;开销敏感数据迁移方案(CA)每次选取效益最大的节点迁移;单位效益最大迁移方案(Packet)选择单位迁移数据量效益最大的节点迁移。通过三种方案的比较,单位最大效益迁移方案的迁移效益最高。 在数据迁移过程中,为了实现操作的规范性,每个节点的一系列操作可以表示成一个四元组 在开销敏感数据迁移算法的基础上,提出单位效益最大迁移算法。该算法运用贪心准则,每一次迁入节点优先选择单位效益最大的迁出节点进行数据迁移。在固定迁移数据量的前提下,根据基于面积的迁移代价模型,首先计算节点j到节点i的迁移代价cost(j,i),迁移代价越小则说明迁移效益越高,所以定义p(j,i)表示节点j到节点i的收益;其次,根据单位迁移效益p(j,i)/wj递减排序,依次选择迁出节点,每个迁入节点生成最优方案;最后,将MI集合中每个迁入节点方案汇总成最终数据迁移方案。 p(j,i)=k/cost(j,i) (5) 图3为9号迁入节点最优迁移方案生成过程。 图3 9号迁入节点最佳迁入方案 (1)1~6号节点分配到MO,7~12号节点归入MI集合。 (2)当9号节点需要数据迁入时,首先分别计算1~6号节点到9号节点的单位迁移效益,然后进行排序(3 1 6 4 5 2)。 (3)优先迁移3号节点数据到9号节点;当3号节点数据迁移完成后,迁移1号节点数据到9号节点;当1号节点迁移完成后,迁移6号节点一半数据到9号节点,至此9号节点饱和,6号节点仍有剩余一半数据迁移到其他节点。 (4)9号迁入节点选择的迁出节点为(3 1 6),分别迁入数据量为(1,1,1/2)。 不断重复上述算法最终得到最优化的迁移方案,当负载均衡的信息熵高于特定阈值,数据迁移结束。 最优迁移方案如算法2所示。 Algorithm2:The optimal scheme for migration Input:MI_set,MO_set; Output:MigrationS Initialize a migrationS,a temporary partition setsT Letlavgbecome the average load repeat mi=lavg-li,i∈MI_set AddmitoT for each node inTdo ifT≠∅ then for each node in MI_set do wj=lj-lavg,j∈MO_set let cost(j,i)be the cost fromjtoi p(j,i)=k/cost(j,i) addp(j,i)/wjtosi sortsi update the state ofjandi else return addsitoS end untilF>threshold 问题描述:数据迁移问题的最优方案S={X1,X2,…,Xi},n为节点数量,节点i迁移方案可以表示成一个n元组:Xi=(x0,x1,…,xn-1),0≤xi≤1;mi表示迁入i节点需要迁入的数据量,即mi=lavg-li;wj表示迁出节点j需要迁出的数据量,即wj=lj-lavg;所以约束条件为: (6) 最优化问题的目标函数用于衡量一个可行解是否是最优解,文中目的是使迁移效益最大,所以最优解使目标函数取最大值: (7) 定理:如果p0/w0≥p1/w1≥…≥pn-1/wn-1,则式7求得的解是最优解[12]。 证明:设Xi=(x0,x1,…,xn-1),0≤xi≤1是贪心算法的解。若节点i所有迁出数据量都能迁移到目标节点,即xi=1,则显然是最优解。不然,则设m是使xm≠1的最小下标。从贪心算法可知,解的形式为: Xi=(1,…,1,xm,0,…,0),0≤xm<1 (8) 如果Xi不是最优解,而另有可行解Yi=(y0,y1,…,yk,…,yn-1)是最优解,使得 (9) 设k是使得yk≠xk的最小下标,显然这样的下标必定存在。下面证明yk (1)若k (2)若k=m,则xk是第k个节点能迁入目标节点的最多数据量,从而yk>xk是不可能的。由于yk≠xk,必定有yk (3)若k>m,这是不可能的,因为xi=0,m 综上所述,必有xk。 假定以xk替换Yi=(y0,y1,…,yk,…,yn-1)中的yk,则Zi=(z0,z1,…,zk,zk+1,…,zn-1),替换前zi=yi=xi,0≤i≤k-1,替换后zk=xk。为了保证Zi是可行解,必须满足: (10) 这意味着因为第k个节点迁入目标节点的数据由yk增加到xk(即zk),则需要减少从Yi中第k+1到n-1节点迁入目标节点的数据量,减少的数据量必须等于增加的数据量,即应当满足式10。经过这样处理后得到的可行解Zi,其前k个分量均与Xi相同。式11计算说明可行解Zi的效益大于等于假定的最优解Yi的效益: (11) 重复上面的替换过程,每替换一个分量得到的新可行解,与贪心法的解Xi相比,新增了一个值相等的分量,最终或者得到一个与Xi完全相等的解,或者表明Yi不是最优解。从式11可知,每一次分量得到的新的可行解的效益不小于前一步的可行解。所以,Xi的效益必定不小于Yi的效益,这就证明了贪心法求解得到的数据迁移方案的可行解必定是最优解。 在实验中,采用RedisLive监测整个集群系统,收集节点性能信息以及负载情况。以Redis-3.2.8作为评估标准,探讨扩展节点对Redis集群整体性能的影响。表1显示了实验的软件和硬件的配置信息。在4台服务器上分别部署2~8个Redis节点组,通过不断增加节点来查看性能情况。单位最大效益迁移算法和Redis集群的迁移以及开销敏感迁移算法分别从迁移时间、CPU使用率和吞吐量进行比较。采用YCSB(Yahoo! cloud serving benchmark)[13]进行测量。 表1 实验配置信息 (1)迁移时间。 在实验过程中,记录不同数量节点的迁移的开始时间和负载平衡的结束时间,得到三种算法(Redis、CA和Packet)的平均迁移时间。图4比较了三种算法的迁移时间。当节点数较少时,三种算法迁移时间大致相同,然而随着节点数的增多,单位最大效益迁移算法越来越优于其他算法。和Redis相比,Packet迁移算法迁移时间优化了6.2%~14.1%,和CA相比,迁移时间减少了4.8%~10.9%。可以想象,当节点较少时,迁移策略节点的选择基本差不多,导致迁移时间没有明显差异,但是当节点较多时,不同迁移策略的选择会导致不同的迁移结果。 图4 迁移固定数据量对应的迁移时间比较 (2)CPU使用。 Redis集群不断添加新的节点,CPU的使用率逐渐加大。图5给出了三种算法在迁移过程中CPU的使用情况。可以看出,无论是User使用率还是Idle使用率,单位最大效益迁移算法都是有优势的。Packet迁移算法可以以最小的CPU使用率获得最大的迁移效益。当然,随着节点数的增加,Xu等[14]提到的CPU的使用可能会出现瓶颈,但是文中主要研究迁移策略的选择,所以这方面不做考虑。 图5 User和Idle CPU的使用情况 (3)吞吐量。 Redis采用基于内存的单线程KV数据库,官方显示吞吐量可以达到105左右[3]。图6显示了三种迁移算法吞吐量的对比。吞吐量和迁移时间相似,Packet迁移算法的吞吐量优于其他两种算法。可以看出,Packet比Redis提高了4.9%~12.5%,比CA优化了1.8%~6.7%。随着节点的扩展,Packet迁移算法会逐渐显示它的优势,节点越多优势越明显。 图6 吞吐量的比较 为了解决Key-Value高可扩展问题,Paiva等[15]通过利用本地模式优化副本放置,以减少节点通信代价,于是他们提出两种新的技术。第一,每个节点以分散的方式优化最能产生数据位置的远程操作;第二,一致哈希通过结合一种新的数据结构来提供有效的概率数据放置。而Miranda等[16]从数据分片入手,从基于表的、基于规则的和伪随机的散列策略中吸取经验,正确评估随机分片策略,提出一种简单而高效的大数据处理策略。这种随机分片策略维护一个表,这个表里保存着之前存储系统插入和删除操作的信息,这样做减少了传递完美负载分配时所需的随机性数量。百万兆级数据的访问,更多的Key-Value存储系统被应用在多核服务器上,常常导致可用带宽的利用率不足,能源效率不高和重载响应时间变长。为了解决这些问题,Xu等[15]提出了Hippos,一种高吞吐量、低延迟和高效的Key-Value存储模型。Hippos将KV移到操作系统内核中,从而消除了大量网络开销和系统调用。Hippos使用Netfilter框架快速处理UDP数据包,几乎完全消除了UDP的请求开销,并结合无锁多线程数据访问,Hippos消除了内部和外部的几个性能瓶颈,大大提高了整体性能。 目前存在的数据库,像关系型数据库和Key-Value数据库因缺少低代价的数据迁移技术,从而制约了数据库的弹性扩展。Das等[17]提出一种迁移技术,称为Albatross,该技术中持久的数据库映像存储在网络连接的存储中,Albatross迁移数据库通过缓存和活动事物状态来确保在允许事物时对事务执行的影响最小,同时保证在故障时的正确性。 云服务的普及使得虚拟机技术日益重要,一个重要的特点是虚拟机技术可以用于负载平衡。虚拟机迁移两个评估标准是总体迁移时间和故障停机时间,目前大多数研究会在两者之间做出权衡。Zhang等[18]从理论上分析了在保证迁移时间和故障停机时间情况下所需要的带宽,接着假设一个确定性模型作为一个简单的例子,这个例子服从伯努利分布,最后在虚拟机运行的工作负载中分析典型的统计特征,并构建基于互惠的工作负载模型,理论上给出满足实时虚拟机迁移的性能指标所需要的带宽值。对于负载管理、节能、日常服务器维护和服务设备质量来说,多层应用程序的实时迁移起着至关重要的作用。和单一虚拟机迁移相比,多个虚拟机迁移是紧密相关的,可能导致一系列相关的迁移问题。在云服务中,Liu等[19]设计并实现了一种迁移虚拟机相关好友的协调系统,该系统中提出了一种自适应网络带宽分配算法,在迁移完成时间、网络阻塞和迁移故障时间方面减少迁移代价。 而Basin等[20]则更加系统详细地介绍了负载均衡策略,提出了一种可以同时支持大规模scans和实时访问的原子KV映射的KiWi模型。KiWi实现了scans无等待和put无锁操作,大大提高了处理效率。同时,融入数据结构优化内存管理,通过chunks定期维护内存,改善内部组织和空间利用,实现了数据再平衡过程。KiWi负载再平衡策略分为七个步骤,通过两个主要函数:rebalance和normalize,利用chunk的三种状态:infant、normal和frozen,将不平衡数据实现再平衡。 Redis最大效益自适应迁移策略是一种提高Key-Value存储扩展性的自适应策略,理论分析和实验证明该策略可以完善Redis集群节点扩展所带来的不足,提高Redis集群系统的性能。Redis单位最大效益自适应迁移策略有以下两点优势:第一,通过实时判断集群系统负载情况解决Redis手动迁移的不足,有策略的数据迁移使其静态存储均衡化,实现系统之间的自适应调控;第二,提出单位效益最大迁移方案来优化迁移策略,此方案每次优先选择单位效益最大的节点进行迁移,直至迁移完成。 但是,Redis是基于内存的存储系统,迁移过程中不可避免产生一定的网络开销,而如何处理热点数据是另一个难点。文中着重考虑迁移策略的改进,对于其他因素有待更深入的探究。2.3 单位最大效益迁移方案
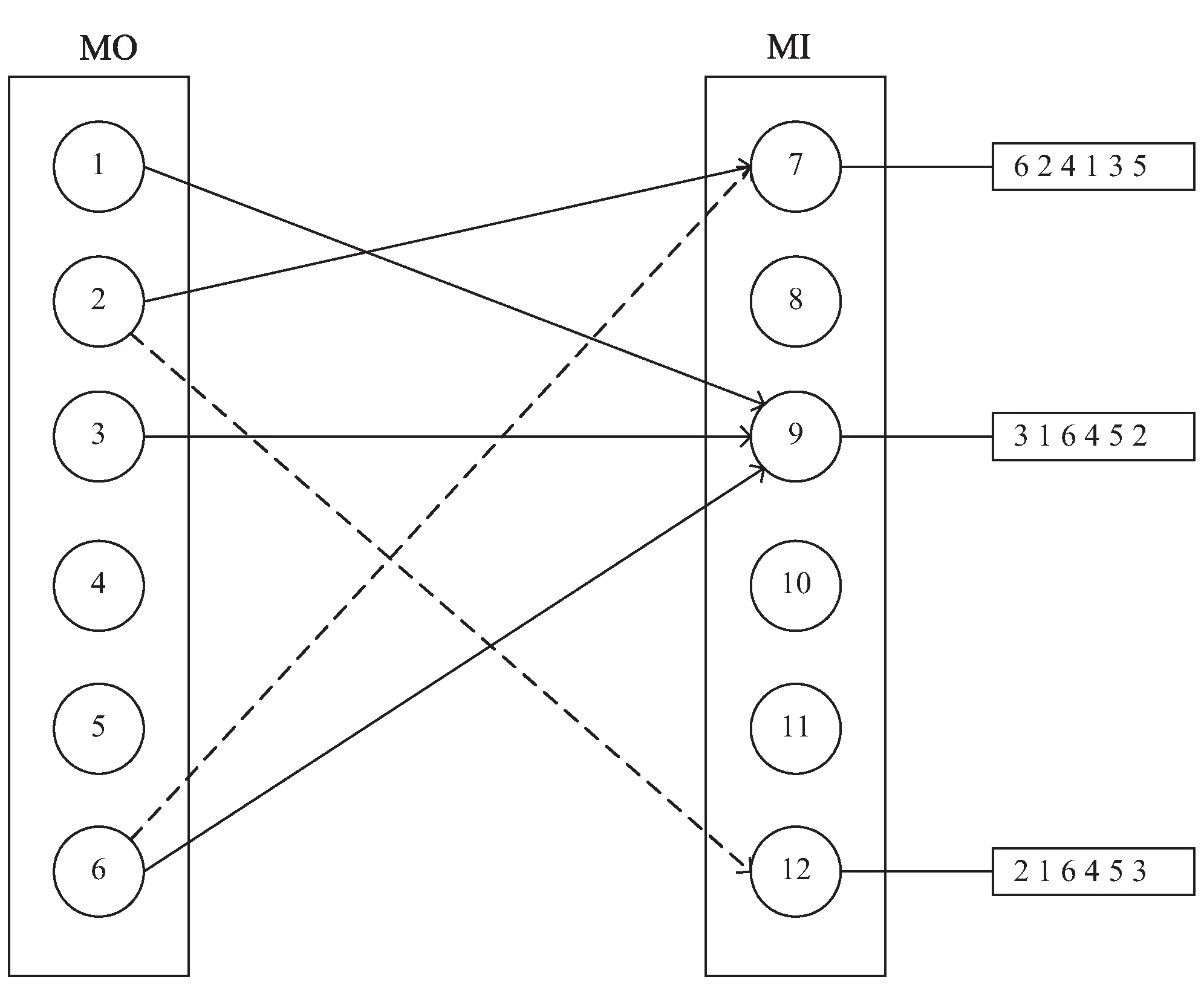
2.4 贪心法求解
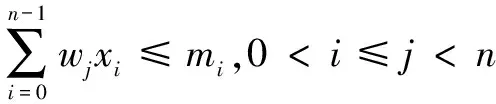
3 实验评估
4 相关工作
5 结束语

