下行贝塔与股票横截面收益:来自中国A股的证据
王志强,胡 玥(东北财经大学 金融学院,辽宁 大连 116025)
一、问题的提出
投资者对资产价格下跌风险的关注程度相对较高,对下跌风险较大的股票要求更高的风险补偿[1]。下行风险是一种在市场普遍下行时个股所遭受的非对称风险,一般采用下行贝塔作为下行风险的代理变量,对于下行贝塔的估计有多种不同方法。Hogan和Warren[2]以二阶下偏距(即半方差)代替方差,得到均值—下偏距均衡模型,并以此得到半方差贝塔,发现半方差贝塔在横截面收益率中的解释能力要优于传统CAPM模型得到的贝塔值。Bawa和Lindenberg[3]曾建议将CAPM模型进行拓展,分别考虑下行贝塔和上行贝塔,以区分个股在不同市场条件下所遭受的风险。Harlow和Rao[4]采用非对称模型对下行贝塔进行估计,发现所得的非对称响应下行贝塔能够有效捕捉到个股的下行风险。Bali等[5]证实下行风险能够在股票横截面收益率中被正确定价,下行贝塔与股票收益率正相关。Ang等[1]则基于条件极值得到下行贝塔,研究发现高下行贝塔往往伴随着高预期收益率。Post等[6]对上述三个下行贝塔进行比较研究,证实半方差贝塔是下行风险的有效代理变量。
国内现有研究大多集中于尾部风险的度量及其与股票收益之间的相关关系。在尾部风险度量方面,张进滔和李竹渝[7]对比了广义Pareto方法下的VaR、ES和Omega三种尾部风险度量指标在尾部风险度量中的适用性。谢尚宇等[8]基于ARCH-Expectile方法对VaR和ES进行了度量。在尾部风险与收益率间关系层面,陈国进等[9]、胡志军[10]借鉴Kelly和Jiang[11]的研究方法,基于极值理论和尾部幂指数分布统计量对下尾风险进行衡量,研究发现下尾风险在股票横截面收益率中具有定价作用。
对于下行风险与股票收益率间的关系,国内相关研究很少。龚旭等[12]用下行已实现半方差作为下行风险的代理变量,研究发现下行风险对行业组合的超额收益率具有较强的解释能力。现有研究尚未从下行贝塔角度对下行风险与横截面收益率间关系进行探讨,下行贝塔在股票横截面收益率中的定价作用未引起足够关注。鉴于此,本文采用半方差下行贝塔、非对称响应下行贝塔、协方差下行贝塔和Estrada下行贝塔作为下行风险的度量指标,考察下行风险与股票横截面收益间的相关关系。
本文可能的学术贡献在于:首先,首次尝试采用四种下行贝塔检验中国A股市场中下行贝塔与股票横截面收益间的相关性。其次,与龚旭等[12]对下行风险与行业组合收益率间关系的研究不同,本文采用组合价差法、Fama-MacBeth回归法从个股层面考察下行风险与股票预期收益率间相关关系。最后,本文还检验了股票市值大小对下行贝塔与股票横截面收益间关系的影响。
二、变量选取与数据来源
本文要检验个股或股票组合的下行贝塔与其预期收益率之间的相关关系,因而检验模型中因变量为个股或者股票组合的预期收益率,预期收益率用下期收益率来度量。
(一)自变量的选择及其计算
1.半方差下行贝塔(βSV)
半方差和下偏距是衡量个股下行风险较为常见的测度方法,尤其在收益率不满足正态分布且非对称的条件下[13]。半方差即为二阶下偏距,它是下偏距的一种特殊情况,是在给定条件下以资产收益率相对于某收益率阈值偏离值平方的期望值来度量的。半方差的计算公式如下:
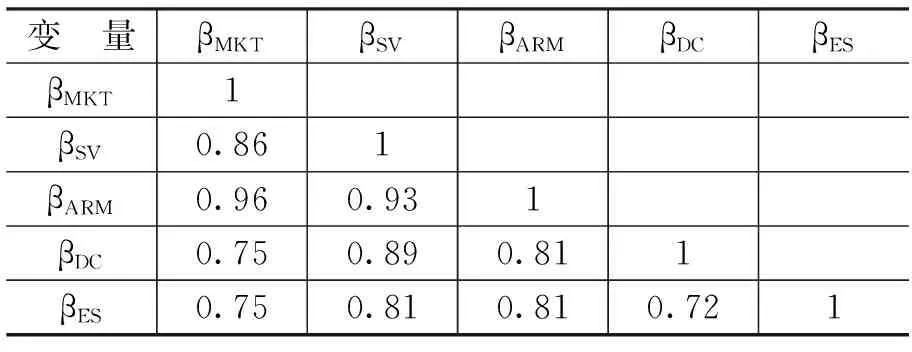
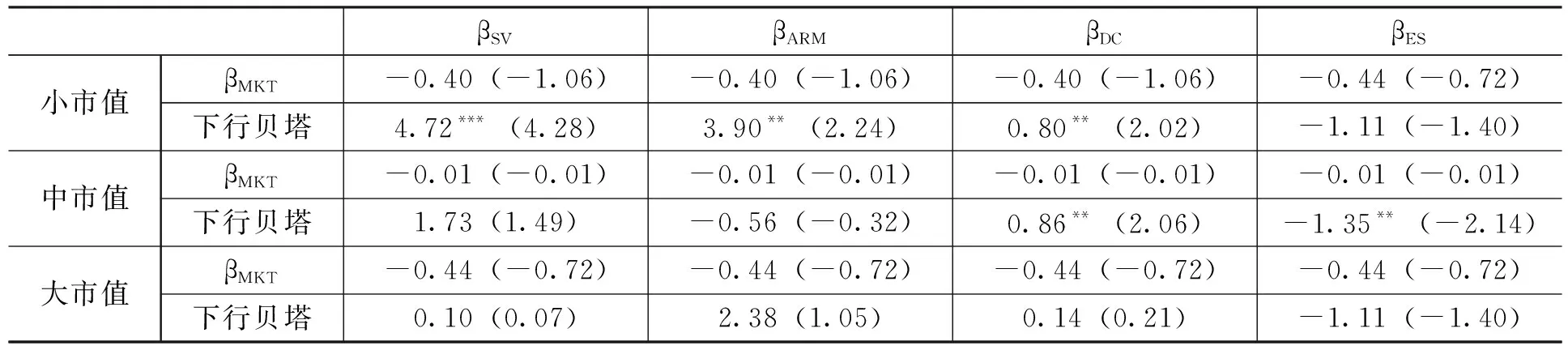
SV=E[(R-k)2|R (1) 其中,R表示某金融资产扣除无风险收益率后的超额收益率,k表示所选择的收益率阈值,相当于设定比较基准组合的收益率,用以区分该金融资产收益率相对于基准组合收益率是上涨还是下跌。 Hogan和Warren[2]与Bawa和Lindenberg[3]将半方差的阈值设定为k=0,在CAPM模型假定的基础上,以半方差代替方差作为系统性风险的测度,并由此得到βSV。本文将延续这一设定,选择0作为区分收益率上涨、下跌的阈值,计算公式如下: (2) 其中,Ri表示扣除无风险收益率后个股i的超额收益率,RM表示扣除无风险收益率后的市场超额收益率。 2.非对称响应下行贝塔(βARM) Harlow和Rao[4]从更一般的均值—下偏距均衡框架出发,采用非对称响应模型(Asymmetric Response Model,ARM)对下行贝塔进行估计,计算公式如下: Ri=αARM,i+βARM,iX+γARM,iZ+εi (3) 其中,X≡RM1RM≤0+E[RM|RM>0]1RM>0,Z≡RM1RM>0-E[RM|RM>0]1RM>0;1RM≤0和1RM>0为两个虚拟变量,1RM≤0表示当市场收益率小于零时其值取1,是市场下行区间虚拟变量,1RM>0为市场上行区间代理变量,且E[1RM≤0]=P[RM≤0]、E[1RM>0]=P[RM>0]。由式(3)可知,在市场上行时,自变量X取值为E[RM|RM>0],通过式(3)得到的βARM不仅测度了市场下行区间内个股与市场的联动性,还在一定程度上考虑了市场上行区间内个股与市场收益率间关系。从风险度量角度来看,由非对称响应模型所得到的βARM与市场贝塔较为接近,它既衡量了个股的下行风险,又与上行风险有关,而并非单纯的下行风险代理变量[6]。 3.协方差下行贝塔(βDC) Ang等[1]基于条件协方差,将下行贝塔定义为当市场收益率小于某阈值时个股收益率对市场收益率回归的条件贝塔。由于本文将收益率阈值设定为0,因而βDC的计算公式如下: βDC,i=cov(Ri,RM|RM<0)/var(RM|RM<0) (4) 为了进一步理解βDC,我们将式(4)展开,得到: (5) 由式(5)可以发现,计算中所使用的均值是在市场收益率满足RM<0条件下个股及市场收益率的条件均值,它不再考虑个股与市场收益率在整个历史区间的联合分布,而是完全基于特定市场条件下的部分收益率分布计算得出的。 4.Estrada下行贝塔(βES) Estrada[14]基于均值—半方差均衡框架、下行协方差和下行方差提出了新的计算方法,如下: βES,i=E{min[(Ri-μi),0]×min[(RM-μM),0]}/E{min[(RM-μM),0]2} (6) 其中,μi、μM分别表示所设定的个股、市场收益率的均值,为了与前文保持一致,我们令μi=0、μM=0,得到: βES,i=E[min(Ri,0)×min(RM,0)]/E[min(RM,0)2] (7) 比较式(7)与式(2)和式(5),我们可以看出,Estrada[14]所提出的βES与βSV、βDC的定义相似,都是基于个股与市场的下行协方差、市场半方差计算得来,衡量的是在市场下行区间内个股对市场组合的风险贡献。而βES与βSV和βDC最主要的区别在于其对个股风险贡献的定义不同。 由各下行贝塔计算公式可知,对βSV、βDC和βES的计算都依赖于满足RM<0条件的部分收益率数据,为了保证样本数据的充足性及下行贝塔估计结果的准确性,本文将下行贝塔的估计期设定为24个月,并采用日收益率数据逐月滚动估计个股的下行贝塔。这种选择主要基于以下两点:一是本文关注市场收益率下行区间内个股与市场收益率的联动性,若估计期较短,则用以计算下行贝塔的交易数据可能较少,致使下行贝塔估计不准确;二是个股的下行风险可能是时变的[1],过长的估计期会使得下行贝塔不能有效反映个股所遭受的下行风险。 1.市场贝塔(βMKT) 为了保证估计结果的可比性,采用过去24个月日收益率数据对βMKT进行估计,公式如下: Ri,t=αi+βMKT,iRM,t+εi,t (8) 2.协偏度(Coskew)与协峰度(Cokurt) 相关协矩的计算区间与下行贝塔的计算区间一致,均采用过去24个月日收益率序列进行计算。协偏度和协峰度的计算公式分别为: (9) (10) 3.特质波动率(IVOL) 本文对特质波动率的定义基于Fama-French三因素模型。计算区间与下行贝塔计算区间保持一致,将过去24个月个股日超额收益率对Fama-French三因素进行回归,回归得到残差值的标准差即为所估计的股票i的特质波动率。其计算方法如下: Ri,t=β0i+β1iMKTt+β2iSMBt+β3iHMLt+ei,t (11) 其中,MKT表示市场因子,SMB表示规模因子,HML表示价值因子;特质波动率为误差项的标准差。 此外,本文还选取了与定价相关的两个财务指标账面市值比(BM)和流通市值(SIZE)作为控制变量。 考虑到1996年12月后中国开始正式实施涨跌停板制度,本文选定样本区间为1997年1月至2018年1月,以在上海证券交易所上市交易的股票作为研究样本,为了保证下行贝塔估计的准确性,剔除估计期内交易日不足60%的股票。由于本文下行贝塔、部分控制变量的计算区间为24个月,因而相关分析实际开始日期为1999年1月。本文以1年期定期存款利率作为无风险利率,样本数据全部来自国泰安金融数据库(CSMAR)。 我们基于过去24个月每月日收益率数据所估计的βMKT、下行贝塔,计算其相关系数矩阵,将所有月份的相关系数矩阵进行时间序列平均即得到相关系数矩阵,如表1所示。 表1 βMKT与各下行贝塔间的相关系数矩阵 从表1可以看出,βMKT、各下行贝塔两两之间均存在较强的相关性。βARM与βMKT的相关系数最高,为0.96,说明两者所揭示的风险特征最相近,与上文分析一致; βDC则与βSV存在较强的关联性;而βES较为特殊,相对于βSV、βARM、βDC,它与βMKT、其他各下行贝塔的相关性则相对较弱。 为判断βMKT、下行贝塔与个股相关特征间的联系,我们分别将个股按照其βMKT、各下行贝塔进行分组,观察各特征因素随个股贝塔值变动的趋势。本文中,我们选取协偏度、协峰度、特质波动率等风险特征、过去1个月收益率(Rt-1)等交易特征、账面市值比及流通市值等公司特征六个变量对各子样本进行描述统计。表2列示了βMKT分组下各下行贝塔及其风险特征的描述性统计。 表2 以βMKT分组的描述性统计结果 注:SIZE为前1个月月末公司实际流通市值的自然对数。IVOL和Rt-1的单位为%。下同。 从表2可以发现,除了βES,其余下行贝塔最高组与最低组间差异值与组间βMKT差异值十分接近,这在一定程度上说明大部分下行贝塔与βMKT具有较强的相关性。除此之外,协偏度、协峰度两个高阶协矩随着βMKT的增大而不断减小,特质波动率与βMKT不存在显著单调关系,Rt-1随着βMKT的增大呈倒U型关系,具有高βMKT的股票更倾向于是小市值、成长型股票。 表3列示了各下行贝塔分组下的描述性统计结果。首先,以βSV分组,最高组与最低组间βSV差值为0.61,而组间βDC差值为0.62,这两者非常接近且明显高于其他下行贝塔的组间差异值;与以βMKT分组类似的是,协偏度、协峰度随着βSV的增大而减小,但最高组与最低组间协偏度差异的绝对值明显高于以βMKT分组后差异;特质波动与βSV间不存在相关关系;βSV的值越大,Rt-1越低;βSV更容易出现在小规模、成长型股票中。其次,以βARM分组,除了βES,最高组与最低组间βMKT、各下行贝塔差值较接近;从特质波动、Rt-1、账面市值比与流通市值角度看,其分组表现结果与以βMKT分组结果十分类似,说明βARM与βMKT揭示了个股相似的风险特征。再次,以βDC分组,我们可以发现,最高组与最低组间βSV的差值0.55是最接近组间βDC差值0.69的,且其余各特征变量分组表现与以βSV分组后表现类似,这说明βSV、βDC所刻画的下行风险特征十分接近,两者存在较强的相关性。最后,以βES分组,最高组与最低组间βMKT、其他下行贝塔的差值明显小于组间βES的差值0.58,而其余特征变量的表现与以βMKT、βARM分组表现类似。 表3 以下行贝塔分组的描述性统计结果 总的来看,βMKT与下行贝塔间存在较强的相关性,其中βSV与βDC两者联系相对更为紧密;协偏度、协峰度与βMKT、各下行贝塔存在明显的负相关关系,而最高组与最低组间协偏度差异的绝对值在βSV和βDC分组中相对较大,负协偏度股票表明其收益率相对于市场而言面临更大下跌风险,说明βSV和βDC对下行风险的捕捉效果较好;特质波动率与βMKT、下行贝塔间不存在明显的单调关系;Rt-1随着βSV和βDC的增大而不断减小,其与βMKT、其他下行贝塔间不存在相关关系;小市值、成长型股票更倾向于拥有高βMKT和高下行贝塔。 1.单因素分组 我们依据过去24个月每月月初日收益率数据所计算的βMKT、下行贝塔分别对个股进行排序,等分五组,并计算各组合未来1个月扣除无风险收益率后组合的等权重超额收益率,组合的构建期与持有期间隔1个月。为了减小组合月收益率自相关性与异方差性对统计检验的影响,本文选择以Newey-West方法调整后t值作为统计推断依据。 以βMKT、各下行贝塔分组后各组的组合收益率均值如表4所示。表4中前两行展示了βMKT与Rt-1间关系,随着βMKT的增大,个股收益率表现出先增大后减小的特征,预期收益率与βMKT呈倒U型关系,βMKT最高组收益率低于最低组,但两者间收益率差异不显著。表4其余部分分别展示了不同下行贝塔分组后的组合收益率。从子样本收益率变动模式看,除了βDC,其余各下行贝塔子样本收益率表现与以βMKT分组后子样本表现类似,均呈现倒U型关系,且下行贝塔最高组和最低组间收益率差异不显著。从最高组和最低组间收益率、贝塔差异角度看,βARM、βES最高组收益率小于最低组,与βMKT分组后子样本表现类似;而βSV、βDC两者则相对接近,下行贝塔最高组收益率均高于最低组。组合收益率表现所揭示的βMKT、下行贝塔间关系与表1、表2和表3所得结论基本一致。 表4 βMKT、下行贝塔组合收益率 注:*、**和***分别表示10%、5%和1%的显著性水平,()内是经Newey-West调整后的t值。组合收益率系数的单位为%。下同。 2.双因素分组 以各下行贝塔分组后,组合收益率并未随着下行贝塔的增大表现出单调增加趋势,并且下行贝塔最高组与最低组间收益率不存在显著差异。考虑到βMKT与各下行贝塔间存在较强的相关关系,单因素分组并不能有效刻画贝塔与预期收益率间关系,为了控制βMKT、各下行贝塔间的相互影响,笔者采用βMKT、下行贝塔双重分组的方式检验预期收益率与下行贝塔间关系。 首先,依据每月月初个股过去24个月βMKT值将全部样本股票分为三组,各组所占比重依次为30%、40%和30%,其中βMKT最小组和最大组各占30%。其次,在各βMKT组内依据下行贝塔值进行排序,等分五组,得到3×5=15个样本组合。最后,控制βMKT对各下行贝塔组的影响,我们将同一等分的下行贝塔组中三个βMKT组的平均收益率作为下行贝塔组的收益率。控制βMKT对下行贝塔的影响后的预期收益率表现如表5所示。 表5 控制βMKT后βMKT、下行贝塔双重分组子样本收益率 单位:% 从表5可以看出,在控制βMKT后,以βSV、βARM和βDC分组,下行贝塔最高组收益率均显著高于最低组收益率,以βES分组后最高组和最低组间收益率仍不存在显著差异。尤其是βSV和βDC,Rt-1与这两个下行贝塔均表现出明显的单调正相关关系,而βARM与预期收益率间并未呈现单调关系,且以βSV、βDC分组后下行贝塔最高组与最低组间月收益率差异值十分接近,约为0.44%,明显高于以βARM分组后的收益率差值0.30%。这说明βSV和βDC在一定程度上刻画了未被βMKT所捕捉到的下行风险。*控制βSV和βDC后各子样本收益数据限于篇幅略去,留存备索。 1.全样本下的Fama-MacBeth回归检验 考虑单变量回归情形下的回归结果如表6所示。 表6 βMKT、各下行贝塔单变量Fama-MacBeth回归估计值 单位:% 从表6可以看出,无论是βMKT还是下行贝塔,其参数估计值均不显著,市场风险、下行风险与个股预期收益率间似乎并没有显著的相关关系,这一回归结果与Fama和French[15]、Post等[6]的研究结论一致,也与本文表4中单因素分组得到的结果一致。 考虑双变量回归情形下的回归结果如表7所示。 表7 βMKT与下行贝塔双变量Fama-MacBeth回归估计值 单位:% 从表7可以看出,在βMKT的基础上增加一个下行贝塔的话,βMKT的估计系数变为负值, βSV、βARM和βDC的参数估计值均显著为正,βES的参数估计值仍不显著。βSV的参数估计值最大,为4.20,βDC的参数估计值最小,仅为1.43。这说明,除了βES之外,其它三个下行贝塔对股票横截面预期收益率会产生更明显的正向影响,这与表5中关于βMKT与下行贝塔双因素分组得出的结果基本一致。 考虑到βMKT与下行贝塔间存在较强的相关性,为了更有效的检验下行贝塔在横截面收益定价中的作用,我们需要在下行贝塔中剔除市场风险的影响以控制βMKT的作用。将个股下行贝塔对βMKT进行回归,所得残差值即为相应的剔除βMKT影响后的下行贝塔,依次作为下行风险的代理变量加入回归方程中,检验在控制βMKT后各下行贝塔对股票预期收益率的影响。该检验结果显示,我们得到类似的结论。*限于篇幅略去,留存备索。 表6和表7中的Fama-MacBeth回归结果表明,βSV、βARM、βDC与预期收益率表现出显著的正相关关系,这与组合价差法结果基本一致。由表3可知,下行贝塔与协偏度、协峰度等风险特征存在一定联系,Rt-1与βSV和βDC存在明显负相关关系,小市值、成长型股票更容易表现出高下行贝塔。Harvey和Siddique[16]证实协偏度在截面资产定价中有重要作用,Fang和Lai[17]证实作为系统性风险代理变量的协峰度也能得到正确定价。Ang等[18-19]发现股票的特质波动率与横截面预期收益率间存在负相关关系。汪炜和周宇[20]证实中国股票市场上“规模效应”表现显著。陈信元等[21]发现账面市值比对中国股票横截面预期收益率有明显解释能力。为了控制个股相关特征对下行贝塔定价效果的影响,进一步明确下行贝塔与预期收益率间关系,以协偏度、协峰度、特质波动率等风险特征、Rt-1等交易特征、账面市值比及流通市值等公司特征共计六个因素作为控制变量加入回归模型中,进行Fama-MacBeth回归。结果显示,控制变量的加入对下行贝塔与股票横截面收益关系有一定的削弱,这与我们的预期一致。 2.流通市值分组Fama-MacBeth回归检验 除此之外,尤其值得关注的是流通市值与下行贝塔间的关系。流通市值与下行贝塔表现出一定的负相关关系,随着流通市值的增大各下行贝塔不断减小,小市值股票更倾向于拥有高下行贝塔。这可能是因为在出现市场收益率普遍下行时,流通市值较大的权重股更容易流入政策资金从而起到稳定大盘的作用,这使得大盘股在市场暴跌时与市场联动性相对而言不会很强,大盘股的下行贝塔相对较低,因而下行贝塔在股票横截面收益中的定价作用可能更多地体现在小市值股票中。Post和Vliet[22]证实下行风险对小市值股票的高收益率具有较强的解释效果。为了考察下行贝塔的定价效果是否在不同规模的股票中存在差异,我们依据每月个股流通市值的大小将样本股票等分为三组,在各流通市值组内分别进行含有上述控制变量的Fama-MacBeth回归。回归结果如表8所示。 表8 流通市值分组Fama-MacBeth回归检验结果 单位:% 限于篇幅,表8只报告了βMKT、下行贝塔的参数估计值。控制了相关特征变量后,在小市值组,βSV、βARM和βDC的参数估计值均显著为正,而βES的估计值不显著,说明βSV、βARM和βDC可以对个股的预期收益率产生正向影响,这一结果与表7的结果完全一致;在中市值组,βSV、βARM的估计值不再显著,βDC的估计值显著为正,βES的估计值显著为负,说明只有βDC能对个股的预期收益率产生正向影响;在大市值组,所有下行贝塔的估计值均不显著。需要说明的是,我们发现βES对中市值股票的预期收益率产生显著负向影响,较高的βES反而会获得较低的风险回报。由βES的定义可知其忽略了市场下行区间内个股与市场收益率变动方向不一致(Ri>0且RM<0)所导致的个股风险贡献减小,而是仅仅考察了Ri<0、RM<0这一种情况,因此,βES可能会高估个股所遭受的下行风险。βES的参数值为负很有可能是因其对个股下行风险的高估所致。 综上,Fama-MacBeth回归结果表明,在控制了βMKT后,βSV、βARM、βDC可以对预期收益率产生显著的正向影响,而βES与预期收益率不存在显著关系。进一步对个股相关特征加以控制,并以流通市值将样本股票进行分组以区分下行贝塔在不同规模股票中的定价效果,研究发现βSV、βARM和βDC在小市值股票中参数估计值显著为正,且其估计值与仅含βMKT单个控制变量回归的估计值差距不大,证实βSV、βARM和βDC揭示了不同于协偏度、协峰度等系统性高阶协矩风险的非对称下行风险。 本文从下行风险角度出发,选用半方差下行贝塔、非对称响应下行贝塔、协方差下行贝塔和Estrada下行贝塔四种下行贝塔作为下行风险的代理变量,采用组合价差法和Fama-MacBeth回归法,考察下行贝塔与股票横截面收益间的相关关系。研究结果显示: 第一,下行贝塔能够有效地刻画个股的下行风险。本文选取的四种下行贝塔中,半方差下行贝塔和协方差下行贝塔对下行风险的捕捉效果相对更好,这两种下行贝塔与个股风险特征指标之间有更强的相关性。 第二,下行贝塔能够解释个股横截面收益的差异性。尽管就单一指标来看,市场贝塔和各下行贝塔对个股横截面收益缺乏解释能力,但是用市场贝塔和下行贝塔双指标解释的时候,半方差下行贝塔、非对称响应下行贝塔和协方差下行贝塔与其股票预期收益显著正相关,且市场贝塔与其股票预期收益显著负相关。这说明,市场贝塔和下行贝塔刻画的风险存在显著的差异。由于市场贝塔既度量上行风险又度量下行风险,而下行贝塔仅度量下行风险,因而扣除下行贝塔对个股横截面收益的影响之后,市场贝塔与个股横截面收益负相关。而且,这种影响在控制市场贝塔的作用后仍然存在。换句话说,上行风险较大的个股其预期收益率较低,下行风险较大的个股其预期收益率较高。 第三,相对而言,半方差下行贝塔、非对称响应下行贝塔和协方差下行贝塔三个变量对小市值股票横截面收益有较强的解释能力,这说明下行风险在小市值股票横截面收益中具有显著的定价作用。笔者认为,从公司层面来看,小市值公司具有较高的经营风险;从股票层面来看,小市值股票具有较大的流动性风险,这些风险决定了小市值股票具有相对较高的下行风险,因而市场会将这种风险进行定价。(二)控制变量的选择及其计算
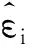
(三)样本说明与数据来源
三、研究结果及分析
(一)描述性统计分析


(二)基于组合价差法的下行贝塔与股票横截面收益关系分析


(三)基于Fama-MacBeth回归法的下行贝塔与股票横截面预期收益关系分析


四、结 论

