基于互信息和PSO-LSSVM的脱硝反应器入口NOx浓度预测

刘延泉， 杨 堃,2， 王如蓓,2

(1. 华北电力大学 控制与计算机工程学院，河北 保定 071003; 2. 河北省发电过程仿真与优化控制工程技术研究中心(华北电力大学)，河北 保定 071003)

0 引言

长期以来，我国发电行业一直以煤炭为主要发电能源，燃煤过程中会产生大量的NOx气体，其不但会危害到动、植物的生长，更会对生态环境造成极大的危害。目前，火电行业运行中排放的NOx已经超过全国排放总量的1/2,大多数火电机组采用选择性催化还原技术(Selective Catalytic Reduction, SCR)对烟气进行脱硝，以降低氮氧化物的排放量，同时使用烟气自动监控系统(Continuous Emisson Monitoring System, CEMS)测量烟气中NOx质量浓度，但由于CEMS对NOx浓度的测量有较大的迟延，无法及时反映SCR反应器入口NOx浓度的变化，因此得不到最佳的喷氨需求量。因此，建立有效的入口NOx浓度预测模型具有重要的意义[1～3]。

机组负荷、煤量、风量、二次风门开度、烟气含氧量等众多因素会同时影响NOx的生成，这些因素间相互耦合，单纯地采用机理构造反应器入口NOx的预测模型有很大局限性。近年来，在NOx生成与排放的预测建模等大量非线性问题的处理中，神经网络和支持向量机等人工智能技术得到了广泛关注[4]，其中，最小二乘支持向量机(Least Squares Support Vector Machine，LSSVM)可以将二次规划的问题转化为线性方程组的求解，大大加快了运算速度，因而在解决实际问题中得到了广泛应用，并且都取得了良好的预测效果[5-6]。LSSVM模型参数的选取对其泛化能力有很明显的影响，主要参数包括惩罚因子C和核参数σ。在建立SCR脱硝反应器入口NOx的LSSVM预测模型时，出于降低模型复杂度、减少训练时间、避免“维数灾难”、易于工作者等方面考虑，需要选出相关性最强的特征作为此预测模型的输入[7～9]。

本文通过对火电厂NOx生成机理及锅炉运行参数进行分析，从统计学的角度出发，基于过滤式评价准则[10]，采用互信息法,在同时考虑了辅助变量和主导变量之间的相关性及辅助变量间的冗余性后，对影响NOx生成的因素进行了筛选，将其作为基于粒子群优化参数的最小二乘支持向量机的输入，建立了NOx生成的预测模型。

1 样本数据处理

1.1 样本优选

为使样本数据集尽可能简单地包含原样本中所有的信息，使用相似度来优化训练样本[11，12]。本文选取了以下相似度函数：

(1)

式中：ω为归一化参数；xi、xj分别表示第i、j组样本数据；Rij表示计算所得xi与xj间的相似程度。

样本优化的原则：判断两组数据相似度Rij与阈值ε的关系，若相似度小于阈值，则保留全部这两组数据；若相似度大于阈值，则删除两组数据中的其中一组，从而达到优化样本集的目的。

1.2 基于互信息的辅助变量筛选

本文主要采用互信息法对辅助变量进行特征变量的筛选。熵H(X)代表平均信息量，即随机变量X不确定性的度量，熵又称为自信息，互信息I(X,Y)可以衡量随机变量之间的相关性，用于评价自变量对因变量所贡献的信息量，是衡量信息相关性的一种方法[13～16]。互信息的公式为[17]：

I(X,Y)=H(X)+H(Y)-H(X,Y)=

H(X)-H(X|Y)=H(Y)-H(Y|X)

(2)

式中：H(X)、H(Y)和H(X,Y)分别为X、Y的熵以及它们的联合熵；H(X|Y)和H(Y|X)分别表示各自的条件熵。条件熵指知道X的情况下，Y的信息量。

(3)

(4)

(5)

式中：熵H(X)为X不确定性的度量，熵越大表示随机变量的随机性越大；px|y(xi,yi)为给定Y时X的条件概率；H(X|Y)则表示随机变量Y给定的情况下随机变量X的不确定性。

评价函数会直接影响到选择算法的最终性能，在基于互信息特征选择算法中起着重要作用。通常直接选取输出变量Y与输入变量Xi互信息值为评价指标，其中，BIF(Best Individual Feature)算法的评价函数如式(6)所示：

J(fi)=I(fi;c)

(6)

式中：fi表示待选变量；c为预测模型的主导变量。

该算法可以在待选变量中选出与主导变量具有最大相关性的辅助变量，但却忽略了已选变量之间存在的信息冗余，而MIFS(Mutual Information Feature Selection)算法将惩罚项引入了评价函数，降低了已选变量之间的信息冗余。MIFS算法的评价函数为：

(7)

式中：fi∈F为待选变量；c为主导变量；β为惩罚因子；Sj∈S为已选变量。

通过式(7)所示评价函数，不仅可以选出与主导变量具有最大相关性的辅助变量，同时兼顾到了待选变量与已选变量之间的冗余性，做到最大可能地减少模型辅助变量的信息冗余。β越大，则表示评价指标将更多地考虑候选变量与已选变量之间的信息冗余。

由于参数β的选择对该算法的筛选效果具有很大的影响，而mRMR(Minimum Redundancy Maxiumum Relevance)算法解决了实际中β较难选择的问题，该算法将可随已选变量集大小变化的参数替代固定的β值，充分考虑了已选变量集对候选变量的影响。mRMR的评价函数为：

(8)

mRMR算法的具体流程如下：

步骤1. 初始化已选变量集合S(初始空集)；初始化待选变量集合F(包含全部的n个变量)。

步骤2.选择待选变量fi∈F，并分别计算fi与输出变量c之间的互信息。

步骤3. 选择首变量：选择通过式(6)中计算出互信息数值最大的变量作为首变量，并将计算出的互信息值进行排序。

步骤4. 贪心搜索：循环计算已选变量fs与待选变量fi之间的互信息，并且根据评价函数J最大的变量fi作为下一变量；与此同时，F=F-{fi}，S=S+{fi}，直到所选变量个数达到预设变量数k。

实践证明，使用这种变量选择的方法筛选出的辅助变量可以建立更加精确的NOx预测模型。

2 PSO-LSSVM原理

2.1 最小二乘支持向量机(LSSVM)

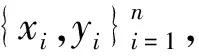
y=f(x)=ωTx+b,i=1,2,…,n

(9)

根据结构风险最小化的原则，将回归问题转化为约束问题，并引入拉格朗日乘子：

L(ω,b,e,α)=J(ω,e)

(10)

式中：α为拉格朗日乘子。

分别对ω,b,e,α求偏微分，得到最优值，进而建立回归函数：

(11)

式中：K(x,xi)为核函数。本文选取径向基函数作为核函数，表示为：

(12)

2.2 粒子群算法(PSO)

PSO(Particle Swarm Optimization)算法是在1995年由Eberhart和Kennedy提出的一种源于对鸟群捕食行为的进化计算技术，PSO在收敛速度以及参数选择等方面较其他优化算法具有一定的优势。其基本思想是将优化问题的所有解构成一个粒子空间，粒子空间中的每个粒子都是优化问题的一个解[18～20]。每个粒子都具有速度、位置及由目标函数决定的适应值，粒子在解空间中寻求最优的适应值。其算法如下所示：

vij(t+1)=ωvij(t)+c1rij(t)(pij(t)-

Xij(t))+c2r2j(t)(pgj(t)-Xij(t))

(13)

Xij(t+1)=Xij(t)+vij(t+1)

(14)

式中各参数的含义如下：

1)i表示第i个粒子，i=1,2,…,M,M是该群体粒子的总数。本文选取M=60。

2)j表示每个粒子中算法所优化的第j个参数。

3)ω表示惯性权值因子，其大小影响整体的寻优能力，为了保证其收敛到全局最优，避免出现早熟收敛的情况，一般采用权值ω在ωmax与ωmin之间线性递减的方法。本文选取ωmax=0.9，ωmin=0.4。

4)t表示此时优化的代数。

5)vij(t)表示粒子i在j维的空间速度。

6)c1和c2为加速因子。本文中选取c1=1.7，c1=1.5。

7)r1j和r2j表示相对独立的2个随机函数，其值在[0～1]之间变化。

8)vij(t)表示粒子i的历史最优解的j维值。

9)pgj(t)=min{pij(t)}表示所有粒子在t时刻的历史最好解的j维值，即所有粒子在所优化的第j个参数中的历史最优解。

10)Xij(t)表示粒子i处于j维空间的位置。

根据式(13)和式(14)进行迭代计算，对粒子位置和速度进行动态更新，计算粒子个体在搜索过程中适应值最优即为个体最优值，其中，适应值根据目标函数来计算。整个种群在搜索过程中达到的最优解则为全局最优值。当群体搜索到满足最小适应值的最优位置或者达到迭代次数之后即可结束计算。

3 入口NOx浓度预测模型的建立及仿真

基于多函数优化样本，将优化后的样本数据使用互信息法筛选出主要的辅助变量，降低数据维度，再利用LSSVM对筛选出来的数据进行训练，并采用PSO算法对LSSVM中的径向基函数宽度参数σ与惩罚因子C进行优化，依此建立NOx浓度的预测模型。

3.1 辅助变量的选择

火电机组锅炉的燃烧过程是一个非常复杂的过程，其具有多变量、耦合性等特点，由于同时会有几十个因素影响NOx的生成，所以辅助变量的选择会在很大程度上影响模型精度及其复杂度。本文的主要辅助变量是通过分析NOx的生成机理并结合文献[6，7，13]选取，主要包括机组负荷、煤量、风量、主蒸汽压力、二次风辅助风门挡板开度、燃尽风挡板开度等46个变量。选取的部分辅助变量如表1所示。

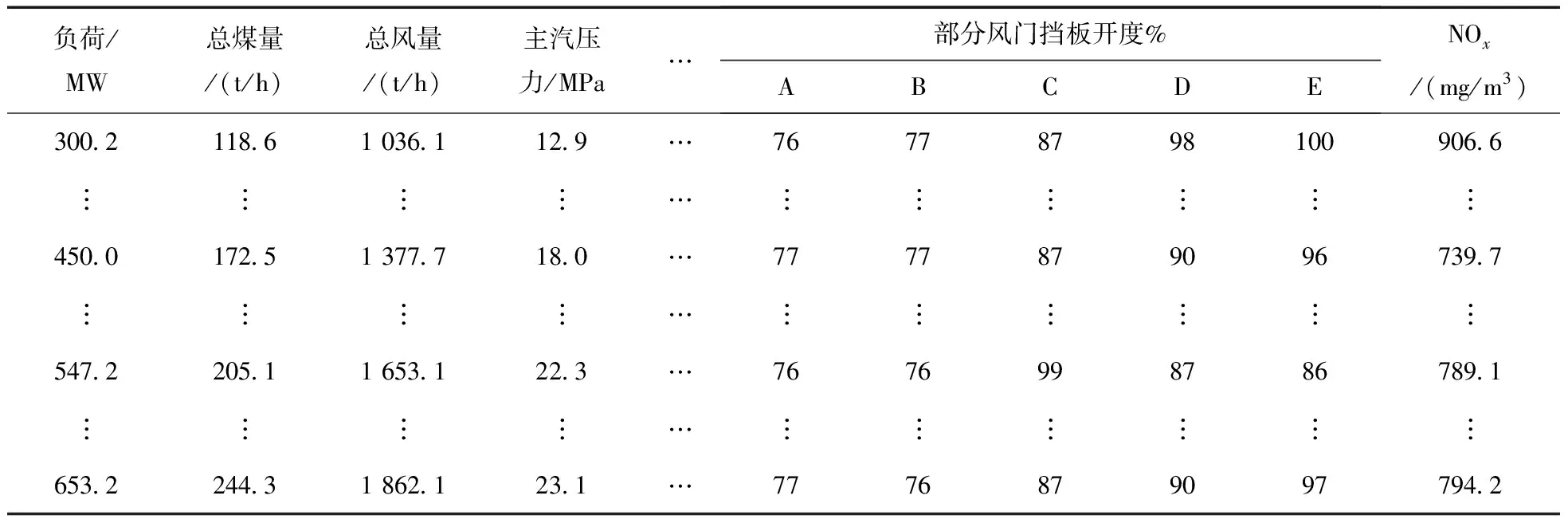
表1 部分初始变量数据展示

注：NOx浓度为A、B两侧数据和。

3.2 筛选数据

本文选取了46个辅助变量，每个变量对应 1 527 个点，以此作为数据样本的集合，利用相似度函数进行样本优选，剩余样本数量随阈值ε的变化而变化，如图1所示。采用式(3)进行优选，当两组数据间的相似度Rij大于阈值ε时，通过删除其中的一组来减少样本的冗余。

从图1中可以看出，当阈值ε位于[0.998,1]时，样本剩余的数量随ε的变化最大，即表示选取此阈值时，相似度函数对于样本的优化的效率最高，本文阈值取0.998 5时，剩余382个样本。

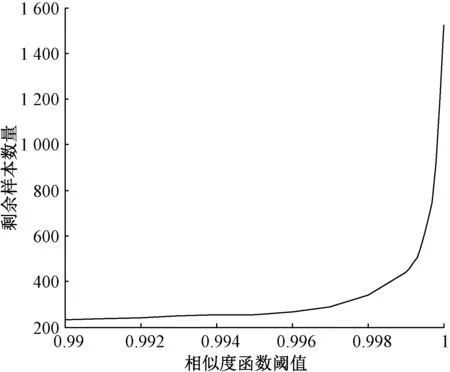
图1 相似度阈值与剩余样本个数之间的关系

使用mRMR算法对基于相似度函数优化后的样本进行辅助变量的筛选，以预测模型输出精度作为度量标准来筛选的辅助变量的个数，建立对主导变量NOx浓度的LSSVM预测模型。筛选出的辅助变量有总风量、后燃尽压力、锅炉蒸发量、总煤量、机组负荷、送风机风门开度、SCR脱硝反应器入口B侧烟温、空预器B侧出口烟温、送风机A侧电流、SCR脱硝反应器入口A侧烟温、主蒸汽温度、空预器A侧进口烟温、空预器A侧出口烟温、空预器B侧进口烟温、送风机B侧电流、主蒸汽压力、B层二次风门2号辅助挡板共17个辅助变量。

3.3 预测结果分析

利用上述方法筛选出的382组运行数据、17个辅助变量，对基于PSO优化参数的NOx生成LSSVM预测模型的可行性与精度进行检验。选取382组数据中的276组数据作为训练集，106组数据作为测试集对预测模型进行测试。LSSVM核函数选择径向基核函数，利用PSO算法对模型中的宽度参数σ与模型惩罚因子C范围进行寻优，经优化后惩罚系数C=235.829 5、核参数σ= 5.038 3，模型的预测结果如图2所示。同时，将未经互信息法筛选的46个辅助变量、382组运行数据作为PSO-LSSVM预测模型的输入，PSO与上面的模型具有相同的初始参数，用模型的输入变量个数作为唯一的变量，仿真结果如图3所示。可以看出，基于互信息对辅助变量进行筛选的PSO-LSSVM模型的预测值更接近实际值。

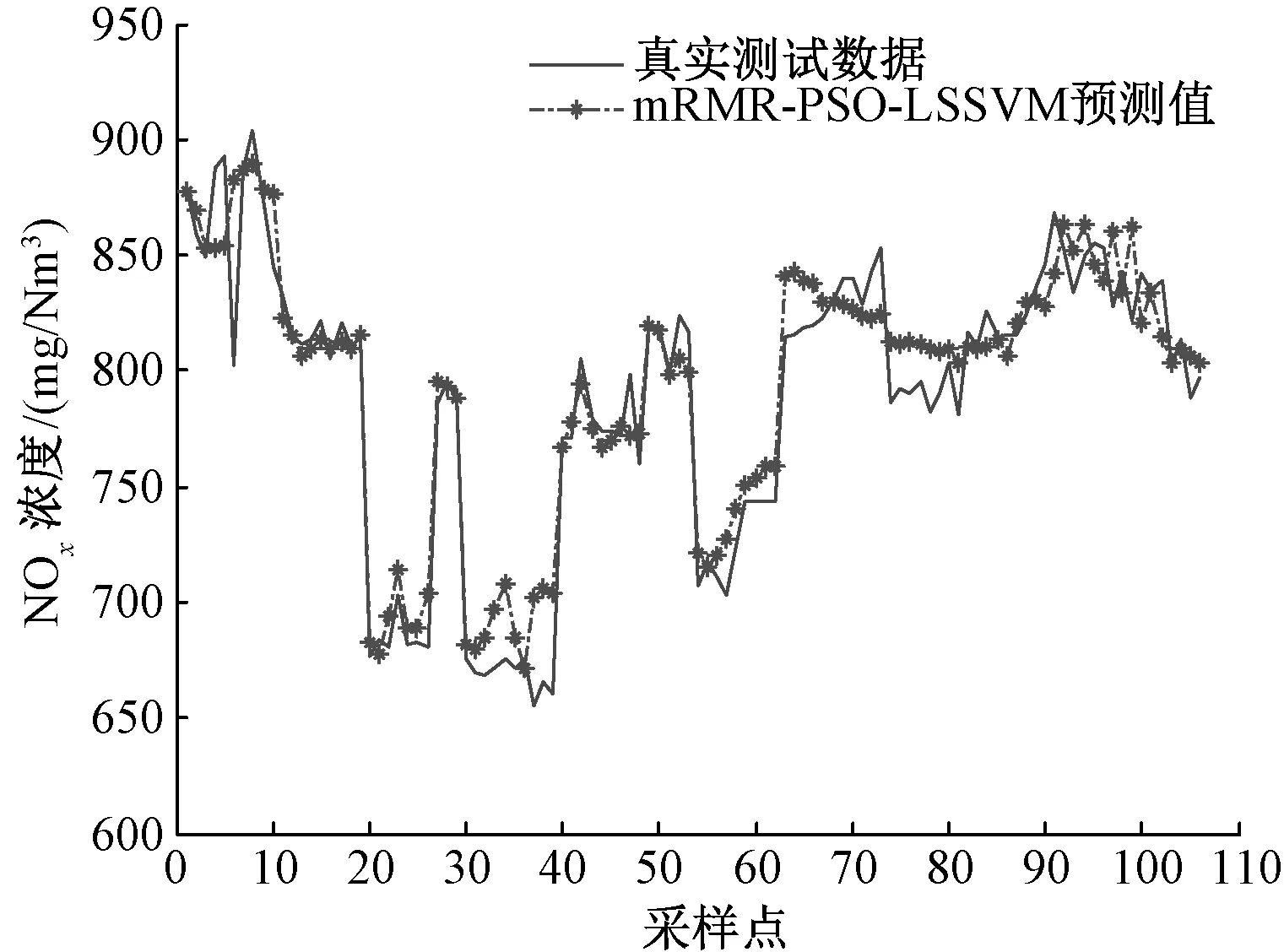
图2 mRMR-PSO-LSSVM预测值与实际值的比较

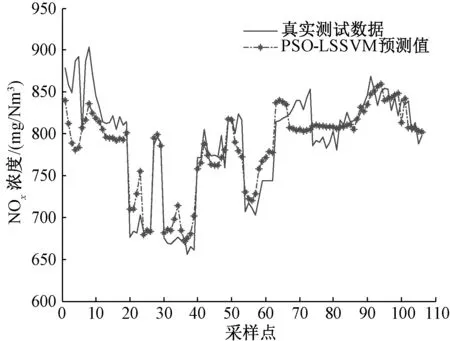
图3 PSO-LSSVM预测值与实际值的比较

为了比较两个模型的预测精度，使用平均相对误差EMRE、均方根误差ERMSE以及拟合度R2来对模型进行评价，其结果如表2所示，由图2与图3对比及表2可知，基于互信息筛选变量的PSO-LSSVM模型预测具有更高的精度。

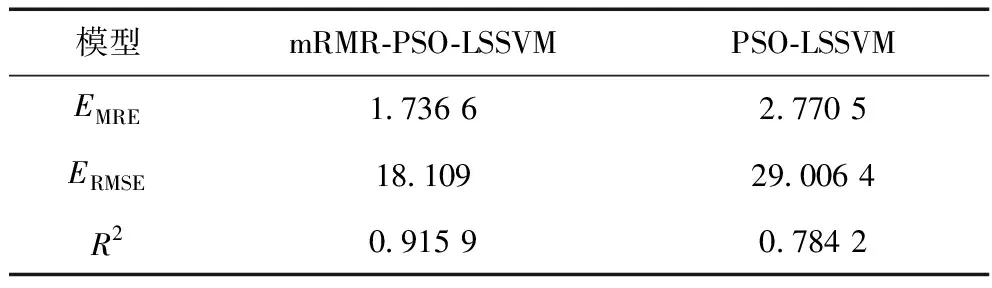
表2 模型误差

4 结论

为了更加准确地测量SCR脱硝反应器入口NOx浓度，本文建立了基于互信息和PSO-LSSVM的预测模型。在建立模型过程中，使用相似度函数减少样本数据之间的冗余性，同时利用互信息法对辅助变量进行了筛选，解决了建模过程中变量选择的问题，建立了mRMR-PSO-LSSVM的NOx生成预测模型，并进行了MATLAB仿真。对比未经互信息法进行变量筛选的PSO-LSSVM模型，该模型降低了辅助变量的维数并减少了变量间冗余性。通过仿真结果可以看出，该模型可以较好地预测脱硝反应器入口NOx浓度的变化，并且具有较高的拟合精度。