基于恒温控制的FDM3D打印机PID系统设计

甘新基, 齐试航, 郑栋, 管明福, 何召龙

(1.%北华大学机械工程学院，吉林吉林 132021；2.中国科学院沈阳自动化研究所海洋机器人卓越创新中心，沈阳 110000)

0 引言

3D打印技术诞生于20世纪80年代，近年来随着科技的进步3D打印技术得到了快速发展，特别是熔融沉积成型（FDM）打印技术因其经济、结构简单的优点得到了广泛的普及和传播，为教育、医疗、工业设计等领域注入了新的生产力[1-7]，甚至近年来有学者已经对3D打印技术实现生物组织再生和生物器官打印进行研究[8-9]。因此3D打印技术是实现工业4.0和我国“2025”计划的一个不可忽视的重要技术。但是采用FDM技术打印的产品普遍存在台阶纹、开裂等表面缺陷[10-11]，分析其主要原因是由于环境空气扰动造成的打印温度不稳定，冷却速度不均匀等问题。邹国林、汪程等[12-14]也通过实验和数据分析对FDM工艺过程进行优化，提高模型的打印质量。杨柏森[15]研究了打印过程中散热条件对FDM丝材黏结质量的影响，认为通风速率、成形室温度、平台温度及分层截面尺寸等因素都会对丝材的黏结强度、尺寸精度以及翘曲变形都会有影响。本文提出了采用PID控制策略实现打印挤出头的恒温控制。

1 PID控制原理

在3D打印机中，打印耗材的温度控制存在热传导和热对流的两种导热方式：一方面采用热传导原理，使用加热电阻将材料加热到熔融状态，使材料具有良好的流动黏性；另一方面为了防止加热腔温度过高或者过低，采用热对流方式开启风扇控制加热腔的温度过高。这两个过程控制的温度变化对模型的质量有着直接的影响。

本文恒温测控算法为PID算法，构建数学模型[16-17]。以ABS成型材料为例，进行加热，温度控制在230℃。在控制系统中，PID算法是根据理想温度设定的值r（t）和实际测量反馈的值c（t）的偏差e（t）来进行比例、积分、微分的调节，如式（1）所示:

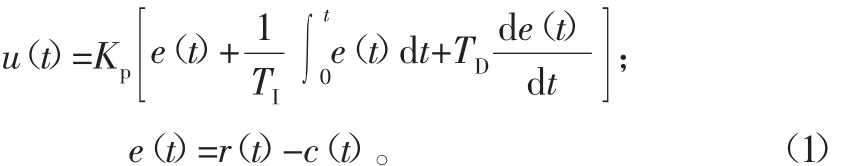
式中:TI为积分时间;TD为微分时间;u（t）为控制器的输出;e（t）为控制器的输入;KP为比例系数。

对于产生的积分和微分连续时间信号要进行离散化处理，Ts为缩短采样周期，用求和代替积分，差商代替微商，从而使PID算法离散化，如式（2）所示：

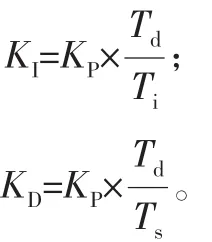
式中:KP为比例系数;KI为积分系数;KD为微分系数。

在加热系统中采用一阶惯性滞后环节建立温控对象数学模型，所以加热模块传函为

式中:K为被控对象静态增益;T为时间系数;τ为滞后时间。

2 仿真实验

采用Matlab的Simulink模块建立PID控制仿真实验系统[18]，如图1所示。Transfer Fcn为传递函数，配置函数：Numerator为0.233，Denominator为25.5，Transport Delay滞后时间为19.5 s。给系统一个300℃的阶跃信号，每相隔10 s采集一次喷头温度并绘制阶跃曲线，并结合拟合曲线求得传函参数值，实验数据见表1。

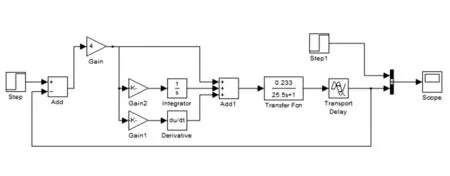
图1 PID仿真结构图

表1 阶跃响应时间数据

图2 阶跃响应曲线

通过表1的数据拟合，得到如图2所示曲线。从图2可以看出响应曲线近似为S型，由Ziegler-Nichols工程整定法可知[19-20]，S型阶跃响应曲线适用延滞一阶惯性环节，验证了传函，运用Cohn-Coon公式 (4)得出：K=0.233，T=25.5，τ=19.5。

式中：ΔC为控制系统输出响应；ΔM为控制系统阶跃输入；t0.28表示升高的温度达到0.28ΔC所用的时间；t0.632表示升高的温度达到0.632ΔC所用的时间。因此传函为

通过PID系数不断试验，验证了当Kp=4、KI=0.26、KD=-19.6时，控制效果达到了需要的精度，当喷头加热到230℃需要12.5 s,超调量8.7%，稳定时间为34 s，如图3所示。但是当环境存在空气扰动时，必然会引起温度起伏，如图4所示。超调量增加的同时稳定时间也增长，但是虽然温度不断发生起伏变化，但是PID控制系统一直可以维持其不失调的状态。

图3 PID控制响应曲线

图4 空气扰动下的PID控制响应曲线

3 结语

本文采用PID控制算法对FDM3D打印机挤出系统进行了温度控制，针对所需要控制的对象，找到了各个控制变量的最佳比例系数，实现了较低超调量的控制效果，对FDM3D打印机的打印精度的提高具有一定的借鉴作用。