微凸体相互作用对界面法向接触特性和能量耗散的影响
王庆朋,张力,唐志刚,张韬
微凸体相互作用对界面法向接触特性和能量耗散的影响
王庆朋1, 2,张力1,唐志刚1,张韬1
(1. 重庆大学 汽车工程学院,重庆,400044;2. 河南农业大学 机电工程学院,河南 郑州,450002)
为了预测粗糙界面上微凸体相互作用对法向接触特性和能量耗散的影响,在确定性接触模型的基础上,增加几何重叠和固体表面能等约束条件,对发生相互作用的微凸体进行等体积合并。通过不同的法向载荷、采样间隔和粗糙度等方案,分析微凸体相互作用对法向接触刚度、阻尼和能量耗散的影响,并与相互独立的结果进行对比。研究结果表明:单个球体的接触面积与测试结果较好地吻合,验证了本研究模型的可行性;粗糙界面上法向接触参量与采样间隔均为正相关;接触刚度和阻尼随着粗糙度的降低而增加,而能量耗散随着粗糙度的降低而增大。对于小的变形量和大的采样间隔,微凸体相互作用可以忽略,但随着变形量增加以及采样间隔减小均有明显的影响,与相互独立的结果相比,法向接触刚度和阻尼变小,而能量耗散增加。
界面;微凸体相互作用;法向接触;能量耗散
在机械系统中,界面上的微凸体起着传递物质、运动和能量的作用,其接触状态对系统的静动态特性、摩擦功耗以及疲劳寿命等都有着重要的影响。对于微型器件来说,微凸体的真实接触状态对系统的影响更为显著。目前,关于粗糙表面接触的研究方法主要有实验分析、概率统计、分形理论、数值计算和确定性理论等。FU等[1–2]通过实验获得界面的法向特征参数,但是,实验结果与接触体的接触状态以及实验环境等因素密切相关,且获得的实验数据有限。在概率统计方法中,通常先分析单个微凸体的接触特性,然后,利用特定的概率密度函数将其拓展到整个粗糙表面,如经典的GW模型[3],但是,未考虑微凸体间的相互作用[4]。CIAVARELLA等[5]基于GW模型,通过改变名义接触压力来考虑微凸体相互作用。ZHAO等[6]通过单个微凸体受力引起相邻微凸体中心下降,将所有发生接触的微凸体引起变形进行叠加,以此来考虑相邻微凸体的影响,随着微凸体数量的增加,所需的计算成本急剧增加。杨红平等[7]采用分形理论,分析了不同接触状态、法向载荷和分形参数等对接触特性的影响,指出由于在模型中忽略接触过程中微凸体间的相互作用,造成计算结果与实验结果存在一定的误差。ZHAO等[6]采用有限元方法对界面法向接触特性进行研究,该方法可以精确地描述接触问题,但是,为了反映实际的粗糙特征,需要大量的单元网 格,而这又需要更多的计算机资源。对于确定性接触模型,应用最多的是GREENWOOD[8]提出的3点峰准则(3PP)。王庆朋等[9]对已有微凸峰确定准则进行总结,针对存在的问题提出“谷−峰−谷”模式的确定准则,可以获得连续的粗糙表面轮廓。已有的确定性接触模型均未考虑微凸体间的相互作用。目前,在接触问题的研究中存在的主要限制是:在2个粗糙表面压缩过程中,其形貌信息始终保持不变,常常忽略微凸体间的相互作用。对于实际界面,接触问题是一个机械、力学、物理、化学、材料和冶金等众多学科交叉在一起的综合问题,所以,表面形貌信息是不可能一成不变的。除此之外,从动态的观点来考虑,未包含微凸体相互作用的接触模型是不完整的。鉴于此,在确定性接触模型的基础上,本文作者基于加载−卸载混合弹塑性机制的接触模型[10],在压缩过程中考虑微凸体间的相互作用,研究界面上法向接触特性和能量耗散与变形量、采样间隔以及粗糙度之间的 关系。
1 模型的建立
1.1 单个微凸体的加载−卸载接触模型
在加载过程中,为了更真实地反映实际的接触情况,本文作者在HERTZ完全弹性和AF完全塑性接触模型的基础上,提出混合弹塑性接触模型[11]。单个球体的接触面积和接触力分别为:


式中:为法向变形量;0为塑性状态下的平均接触应力;和分别为等效弹性模量和球体半径,
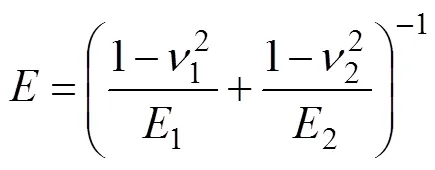
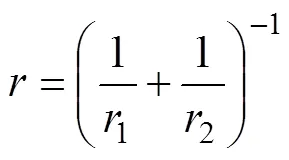
在式(1)和式(2)中,1()和2()分别为弹性和塑性状态所占的比例系数,即
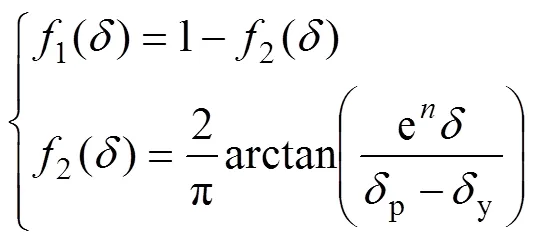
式中:为Meyer硬度指数;y和p分别为初始屈服点和完全塑性屈服点对应的法向变形量。
在卸载过程中,将其视为弹性过程,并且不存在反向屈服现象,则卸载载荷u为

式中:d为变化的曲率半径;r为残余变形量。

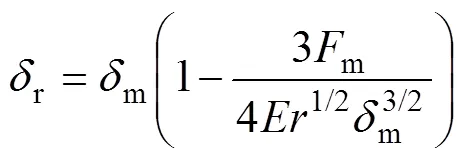
式中:m为最大变形量;m为最大受力。
单个球体的法向接触刚度可表示为
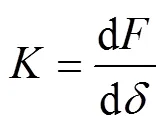
混合弹塑性状态下的法向接触刚度ep为
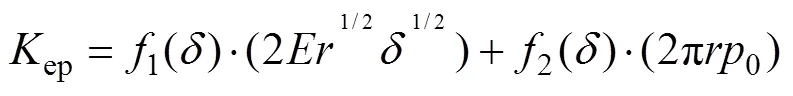
在加载和卸载过程中,得到相应的法向接触力−变形量曲线,曲线形成封闭区域的面积即为界面上储存或耗散的能量,弹性载荷e对应储存的能量e为

单个球体所耗散的能量ep为
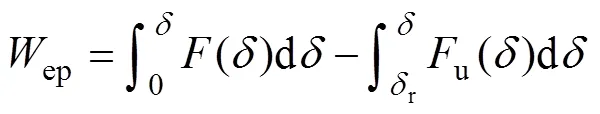
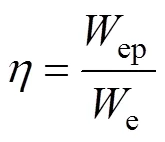
根据文献[10],单位质量量纲一法向接触阻尼为
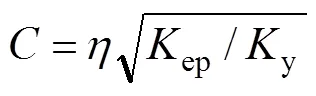
式中:y为初始屈服点处的法向接触刚度。
1.2 粗糙表面轮廓
采用分形理论获得1组2维粗糙表面轮廓,采样长度为800 μm、采样间隔为0.50 μm时的粗糙度a和q,如表1所示。利用文献[9]中提出“谷−峰−谷”模式的微凸峰确定准则得到等效粗糙表面,如图1所示。从图1可以看出:等效表面具有连续性,这为压缩过程中接触特性和能量耗散的演变提供1个基准。
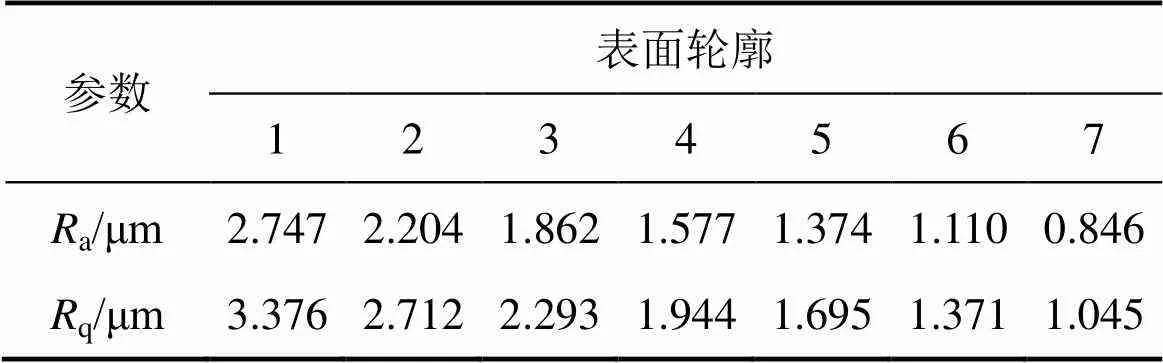
表1 表面轮廓的粗糙度
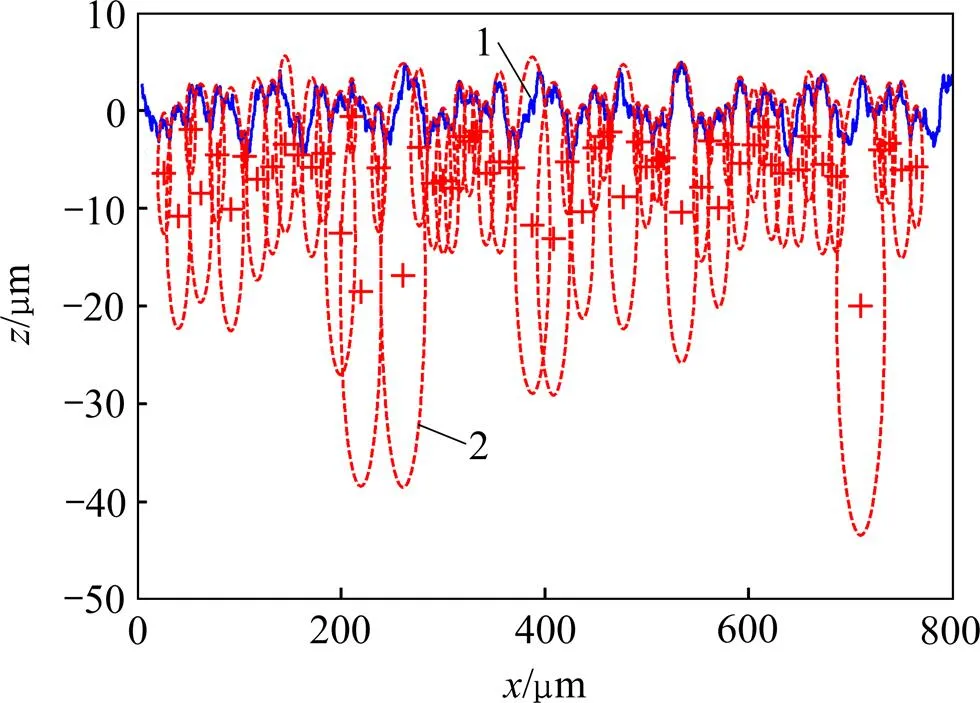
1—原始轮廓;2—等效圆。
1.3 微凸体的相互作用
对于实际界面上的微凸体,由于受到法向载荷的作用,2个相邻的微凸体可能合并为1个较大的,就像板块之间的运动导致山峰的形成一样,所以,表面形貌信息是不可能一成不变的,而是处于不断重构的过程中。其实,界面处表面形貌的变化与地球板块运动有着相似的变化规律,只是在尺度上存在差异。
固体表面能是由于表面分子间化学键遭到破坏,使表层原子朝向体相外侧的键能无法得到补偿而具有的额外能量,也可以理解为改变单位长度所需要的力。为了简化分析,认为微凸体在法向载荷作用下发生碰撞,当出现几何重叠和超过固体表面能时将导致“大山峰”的形成。
为了有效地表征微凸体间的合并,增加约束条件:
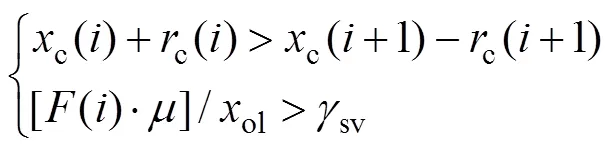
式中:c为等效圆圆心的横坐标;c为接触圆半径;为摩擦因数;ol为重叠长度;sv为固体表面能;为发生接触的第个微凸体。
当满足条件时,将发生相互作用的等效圆基于面积相等进行合并,存在

式中:为新生成圆的半径。
计算得到新生成圆的半径后,再利用合并前相邻2个圆的左、右端点就可以确定新生成圆的位置,为下一个压缩步长提供新的表面轮廓。
1.4 粗糙表面轮廓的接触特性
对于粗糙界面来说,法向接触参量的计算结果就是在压缩过程中所有发生接触球体相应数值之和,则总的法向接触刚度t、阻尼t和能量耗散t分别为
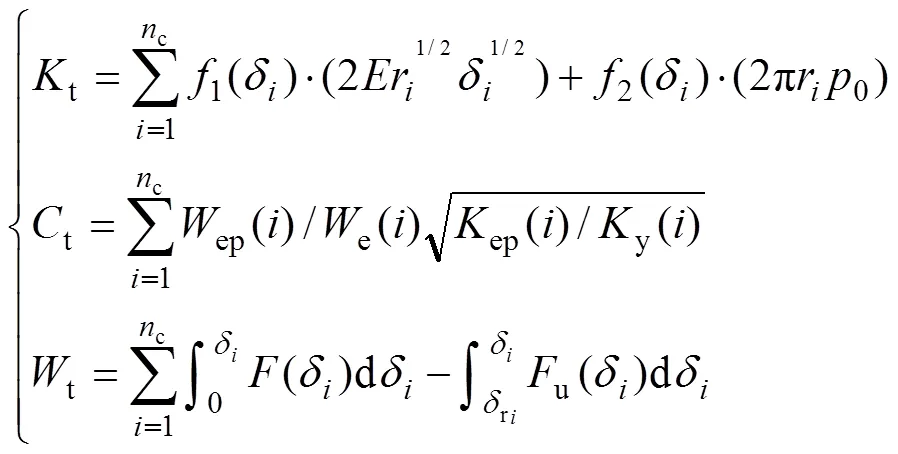
式中:c为发生接触的微凸体数量。
2 计算结果与分析
为了分析微凸体相互作用对粗糙界面上法向接触刚度、阻尼和能量耗散的影响,根据GW模型的建模方法[3],将2个粗糙表面的接触视为1个具有等效粗糙度的表面与1个刚性光滑平面接触。采用不同法向载荷、采样间隔和粗糙度等方案,同时,与相互独立的结果进行对比。采用JAMARI等[12]利用金刚砂平板对一铝合金球进行压缩的实验结果,如表2所示,取铝合金材料的固体表面能sv为77.8 mJ/m2,摩擦因数为0.06。
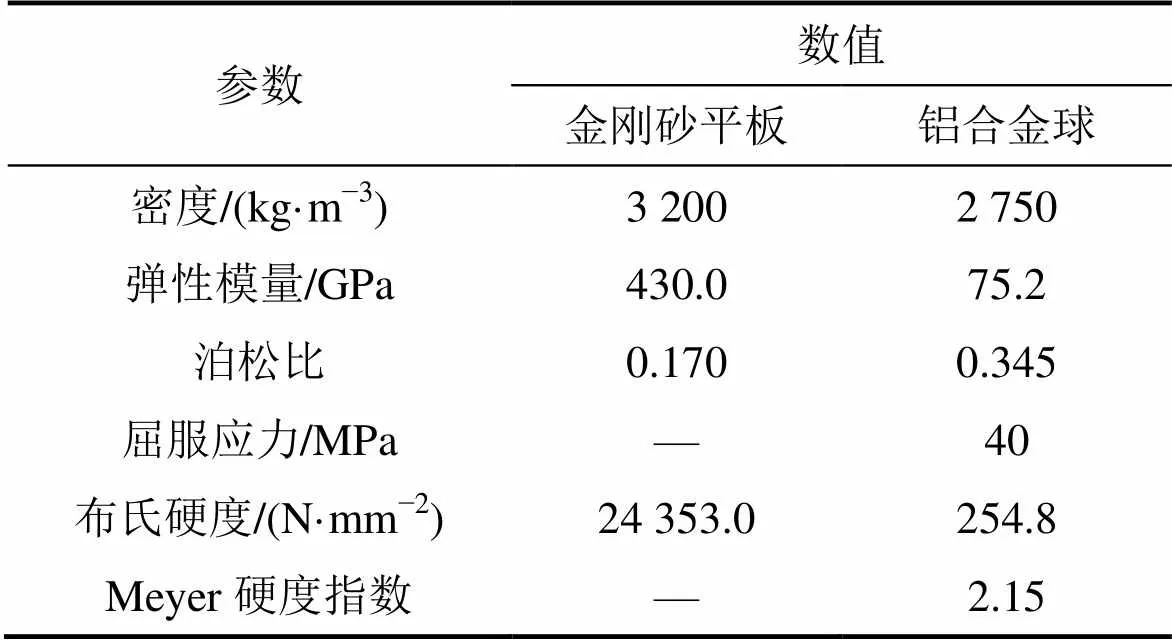
表2 JAMARI等[12]所做实验中测试试件的参数
2.1 模型的验证
为了便于不同结果的比较,将球体初始屈服点的法向参量作为参考值,对计算结果进行量纲一化,同时,与采用文献中的经典模型[13−17]所得结果进行对比。对于粗糙表面来说,将采样长度视为一等效球体的直径,进而将等效球体初始屈服点作为参考点。
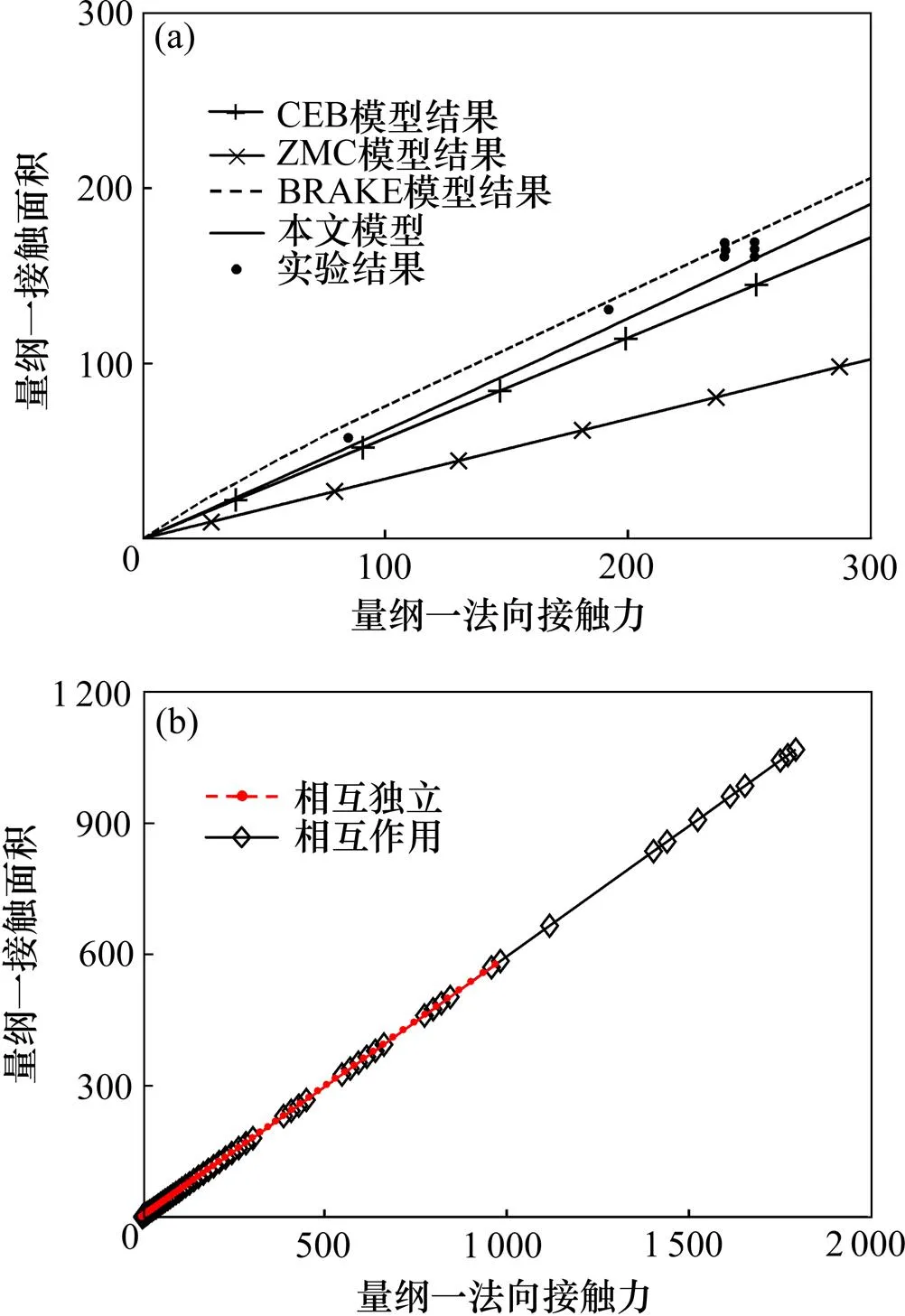
接触面积与法向接触力的量纲一化曲线如图2所示。由图2可知:从与实验测试结果的吻合程度来 看,本文模型所得结果能够较好地与其吻合,其次是BRAKE[13]和CEB[14]模型,而ZMC模型[15]则有较大的偏离;对于2种作用方式,接触面积与量纲一化法向接触力均为线性关系,这与GW[3]和BGT[16]模型的 理论分析结果以及文献[17]中的数值分析结果是一致的。
2.2 法向载荷作用下的接触特性
为了分析法向载荷作用下接触特性的变化规律,采用表面轮廓4,采样间隔取为0.50 μm,法向变形量为等效粗糙峰中的最大峰值,取60个计算步长。不同接触特性与变形量之间的关系如图3所示。
从图3(a)可以看出:随着变形量的增加,接触刚度单调增加。由于粗糙表面在压缩过程中不断地有新的微凸体参与接触,导致曲线不光滑,这与文献[10]中单个球体的结果是1条光滑曲线有所不同。对比微凸体相互独立和相互作用2种方式,当变形量较小时,微凸体间的相互作用较弱,随着变形量的增加,其造成的影响也越来越明显,考虑相互作用的结果比相互独立的结果小。在压缩过程中,当2个相邻的微凸体满足给定条件时将合并为1个“大山峰”,事实上,这增加了法向变形量,意味着在微凸体中有更大比例的塑性成分,导致接触刚度下降。由图3(b)可知:在较小的法向变形量时,接触阻尼存在1个较大的波动,随后开始下降;当微凸体间存在相互作用时,接触阻尼下降得更快。从图3(c)可知:能量耗散与变形量相对应,随着变形量增加,所耗散的能量增加。与相互独立的结果相比,考虑微凸体间相互作用的粗糙表面具有更多的能量耗散,这与法向接触刚度降低的原因是一致的,主要是因为塑性成分所占比例增加。
(a) 量纲一单个球体;(b) 量纲一粗糙表面
2.3 不同采样间隔下的接触特性
为了分析不同采样间隔对接触特性的影响,法向变形量和计算步长与2.2节中的一致,采样间隔分别为0.05,0.10和0.30,以及0.50~5.00 μm之间每隔 0.50 μm进行1次取值。不同接触特性与采样间隔之间的关系如图4所示。由图4可知:从整体变化规律来看,法向接触刚度、阻尼和能量耗散均随着采样间隔的减小而相应地变小。对于微凸体相互独立和相互作用这2种方式,在较大的采样间隔时,两者的量纲一法向接触刚度曲线是重合的,也就是说,微凸体间的相互作用不明显。当采样间隔小于3 μm时,微凸体相互作用开始变得明显,并且随着采样间隔的减小,两者之间的量纲一法向接触刚度曲线差距变得更大。这主要是因为当采样间隔减小时,粗糙表面上呈现更多精细的微观结构,在压缩过程中也就更容易发生相互作用。

(a) 量纲一法向接触刚度;(b) 量纲一法向接触阻尼;(c) 量纲一能量耗散

(a) 量纲一法向接触刚度;(b) 量纲一法向接触阻尼;(c) 量纲一能量耗散
2.4 不同粗糙度下的接触特性
采用采样间隔为0.50 μm对7个表面轮廓进行分析,不同接触特性与粗糙度之间的关系如图5所示。由图5可知:法向接触刚度和阻尼的变化规律较一致,均为随着粗糙度的减小,量纲一法向接触刚度和阻尼增大。但是,对于不同的作用方式,接触刚度基本上表现为2条平行线,而考虑微凸体相互作用的接触阻尼的增长率明显比相互独立的低。能量耗散的变化趋势与接触刚度和阻尼的变化趋势相反。当粗糙度较大时,2种作用方式之间存在较大的差距,相互作用的结果大约是相互独立的2倍,而当粗糙度逐渐减小时,2种作用方式之间的差距也在相应地缩小。

(a) 量纲一法向接触刚度;(b) 量纲一法向接触阻尼;(c) 量纲一能量耗散
3 结论
1) 通过接触面积的对比分析,单个球体的接触面积可以与测试结果较好地吻合,并且优于其他模型的结果;粗糙表面的结果与文献中的理论、数值分析结果一致,验证了本文模型的有效性。
2) 法向接触刚度和能量耗散随着变形量的增加而变大,而法向接触阻尼在较小变形量时存在1个较大的波动,随后开始下降。
3) 法向接触参量与采样间隔均为正相关;接触刚度和阻尼随着粗糙度的降低而增加,而能量耗散却表现出相反的变化趋势。
4) 对于小的变形量和大的采样间隔,凸体间的相互作用可以忽略,但随着变形量增加以及采样间隔减小,均有着明显的影响。与相互独立的结果相比,法向接触刚度和阻尼减小,而能量耗散增加。
[1] FU Weiping, HUANG Yumei, ZHANG Xueliang, et al. Experimental investigation of dynamic normal characteristics of machined joint surfaces[J]. ASME Journal of Vibration and Acoustics, 2000, 122(4): 393−398.
[2] KONOWALSKI K. Experimental research and modeling of normal contact stiffness and contact damping of machined joint surfaces[J]. Advances in Manufacturing Science and Technology, 2009, 33(3): 53−68.
[3] GREENWOOD J A, WILLIAMSON J B P. Contact of nominally flat surfaces[J]. Proceedings of the Royal Society of London, 1966, 295(1442): 300−319.
[4] GREENWOOD J A. A simplified elliptic model of rough surface contact[J]. Wear, 2006, 261(2): 191−200.
[5] CIAVARELLA M, GREENWOOD J A, PAGGI M. Inclusion of “interaction” in the Greenwood and Williamson contact theory[J]. Wear, 2008, 265(5/6): 729−734.
[6] ZHAO Bin, ZHANG Song, QIU Zheng. Analytical asperity interaction model and numerical model of multi-asperity contact for power hardening materials[J]. Tribology International, 2015, 92(5): 57−66.
[7] 杨红平, 傅卫平, 王雯, 等. 基于分形几何与接触力学理论的结合面法向接触刚度计算模型[J]. 机械工程学报, 2013, 49(1): 102−107.YANG Hongping, FU Weiping, WANG Wen, et al. Calculation model of the normal contact stiffness of joints based on the fractal geometry and contact theory[J]. Journal of Mechanical Engineering, 2013, 49(1): 102−107.
[8] GREENWOOD J A. A unified theory of surface roughness[J]. Proceedings of the Royal Society of London, 1984, 393(1804): 133−157.
[9] 王庆朋, 张力, 杜宝程, 等. 粗糙表面确定性接触模型中峰的再定义[J]. 西安交通大学学报, 2016, 50(11): 115−120. WANG Qingpeng, ZHANG Li, DU Baocheng, et al. Re-definition of asperity-peak for deterministic contact model on rough surfaces[J]. Journal of Xi'an Jiaotong University, 2016, 50(11): 115−120.
[10] 王庆朋, 张力, 唐志刚, 等. 粗糙结合面法向接触的能量耗散与阻尼特性研究[J]. 振动与冲击, 2017, 36(2): 129−133. WANG Qingpeng, ZHANG Li, TANG Zhigang, et al. Energy dissipation and damping characteristics for normal rough contacts of joint surfaces[J]. Journal of Shock and Vibration, 2017, 36(2): 129−133.
[11] 王庆朋, 张力, 尚会超, 等. 考虑应变硬化的混合弹塑性接触模型[J]. 西安交通大学学报, 2016, 50(2): 132−137.WANG Qingpeng, ZHANG Li, SHANG Huichao, et al. Mixed elastic-plastic contact model considering strain hardening[J]. Journal of Xi’an Jiaotong University, 2016, 50(2): 132−137.
[12] JAMARI J, SCHIPPER D J. Experimental investigation of fully plastic contact of a sphere against a hard flat[J]. ASME Journal of Tribology, 2006, 128(2): 230−235.
[13] BRAKE M R. An analytical elastic plastic contact model with strain hardening and frictional effects for normal and oblique impacts[J]. International Journal of Solids and Structures, 2015, 62(1): 104−123.
[14] CHANG W R, ETSION I, BOGY D B. An elastic-plastic model for the contact of rough surfaces[J]. ASME Journal of Tribology, 1987, 109(2): 257−263.
[15] ZHAO Y W, MAIETTA D M, CHANG L. An asperity microcontact model incorporating the transition from elastic deformation to fully plastic flow[J]. ASME Journal of Tribology, 2000, 122(1): 86−93.
[16] BUSH A W, GIBSON R D, THOMAS T R. The elastic contact of a rough surface[J]. Wear, 1975, 35(1): 87−111.
[17] PAGGI M, CIAVARELLA M. The coefficient of proportionalitybetween real contact area and load with new asperity models[J]. Wear, 2010, 268(7/8): 1020−1029.
(编辑 刘锦伟)
Normal contact properties and energy dissipation of interface considering asperity interaction
WANG Qingpeng1, 2, ZHANG Li1, TANG Zhigang1, ZHANG Tao1
(1. School of Automotive Engineering, Chongqing University, Chongqing 400044, China; 2. School of Mechanical and Electrical Engineering, Henan Agricultural University, Zhengzhou 450002, China)
Based on the deterministic contact model, a model with asperity interaction was developed to predict the effects on the normal contact properties and energy dissipation of rough interface. The constraint conditions like overlapping contact spots and the solid surface energy were added to the geometrical model, and the asperities with interaction was merged to create a larger cluster with equivalent area. The effects of the interactions between asperities on normal contact stiffness, damping and energy dissipation were analyzed through various normal loadings, sampling intervals and roughnesses, and then compared with the results of independent asperities. The results show that the contact area has good agreement with the measurements for the individual sphere. The feasibility of this research model is thus verified. The correlation between normal contact parameters of rough interface and sampling interval is positive. The normal contact stiffness and damping increase with the decrease of roughness, but the energy dissipation shows an opposite trend. The differences between independent asperities and interactive asperities at smaller displacements and larger sampling intervals become almost negligible. However, there is a significant change occurs when the greater normal displacements and smaller sampling intervals are applied, which leads to the decrease of the normal contact stiffness and damping and the increase of the energy dissipation.
interface; asperity interaction; normal contact; energy dissipation
10.11817/j.issn.1672-7207.2018.09.010
TH113
A
1672−7207(2018)09−2184−07
2017−10−17;
2017−12−21
国家自然科学基金资助项目(51175530) (Project(51175530) supported by the National Natural Science Foundation of China)
张力,博士,教授,博士生导师,从事内燃机燃烧学、动力学和摩擦学研究;E-mail: zhangli20@cqu.edu.cn

