稀疏度自适应的广义正交匹配追踪算法
张龙
(上海海事大学信息工程学院,上海201306)
1 压缩感知理论简介
压缩感知理论[1-3](Compressed Sensing,CS)最开始由Candes、Donoho和Tao等率先进行研究。只要目标信号相对于某个域是稀疏的或者是可压缩,就可以用观测矩阵将将高维信号投影到一个低维空间上。再求解一个优化问题就可以高概率重构出原信号。理论依据如下:
(1)设长度N的信号x在正交基ψ上是稀疏度为k;
(2)如果能找到一个与ψ不相关的观测基φ;
(3)用观测基Φ观测信号得到长度为M的一维测量值M个观测值Y,K小于M远远小于N;
(4)那么就可以利用最优化方法从观测值Y中高概率恢复X。

图1 压缩感知理论框架
在上述的理论下,采样速率不再取决于信号的带宽,而在很大程度上取决于两个基本准则:稀疏度和非相关性(也叫等距约束性RIP)。
压缩感知理论主要包括三部分:
(1)信号的稀疏表示。稀疏性简单点的解释就是信号含有k个非零值,其他系数值为零或远小于k个非零值。现实中的大多信号x往往并不是稀疏的,所以需要在某个对应的稀疏基上进行稀疏表示。一般的自然信号x本身并不是稀疏的,需要在某种稀疏基上进行稀疏表示。
x=Ψθ
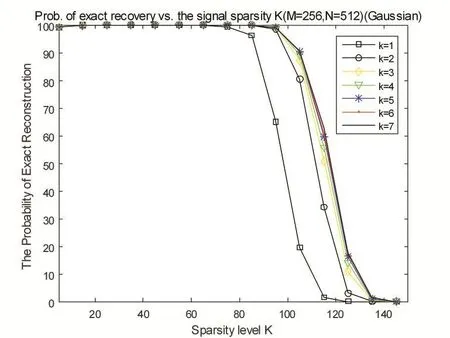
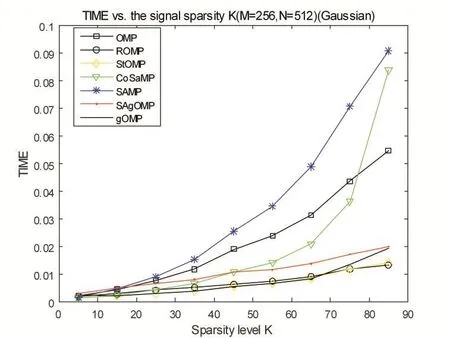
Ψ为稀疏基矩阵,θ为稀疏系数(θ只有K个是非零值(K< (2)设计测量矩阵Φ(也称观测矩阵),我们既要考虑到降低维数来使信号更加简单便于应用于实际,又要考虑实际保证信号的损失最小,保证能够从观测值准确重构信号。目前研究表明只要观测基矩阵与稀疏基矩阵的乘积即重构矩阵满足RIP性质(有限等距性质): 上述性质保证了原空间到稀疏空间的一一映射关系,保证了唯一性,只要观测矩阵中抽取的M列向量构成的矩阵是非奇异的,我们就能从观测信号中通过重构算法恢复原始信号。且若Ψ和Φ不相关,则其很大概率满足RIP性质。CandeS和Tao的研究表明了测量矩阵如果是独立同分布的高斯随机矩阵,那么它将是良好的压缩感知测量矩阵。因此我们用测量矩阵Φ(MxN且M< y=Φx=ΦΨθ=Aθ。 (3)设计恢复信号的算法,利用测量所得的M个值来无失真地恢复原始信号,长度为N。当Φ满足RIP性质,我们先求解上式中的θ,然后将稀疏度为k的信号x从M维的测量投影值y中正确地恢复出来。其中恢复信号的最直接办法是通过l0范数(0-范数,也就是向量yˆ中非零元素的个数)下求解的最优化问题,从而得到稀疏系数θ的估计θˆ。则原信号: 从压缩感知理论诞生至今,国内外学者对设计信号的恢复算法即重构算法提出了多种快速有效的算法,主要包括基追踪算法、贪婪算法、迭代阈值算法等[4,5]。由于贪婪算法相对较快,受到学者们广泛关注。贪婪算法主要有OMP(正交匹配追踪)算法[6]、ROMP(正则化正交匹配追踪)[7,8]、CoSaMP[8](压缩采样匹配追踪),StOMP[8](分段正交匹配追踪)、SAMP[10](稀疏度自适应匹配追踪)、gOMP(广义正交匹配追踪)。前面的4种算法都要假设信号的稀疏度已知,这在实际应用中是不可能的。所以提出了RAMP,可以对稀疏度进行估计且具有较高的重构精度,但是当数据N增大时,算法运行时间过长,实际应用性降低。本文在在保证运算速度的基础上,结合了稀疏度估计,提出了SAgOMP(稀疏度自适应的广义正交匹配追踪算法)。 本文提出的稀疏度自适用广义正交匹配追踪算法(SAgOMP)算法。在针对gOMP需要知道信号稀疏度的情况下,本算法先进行稀疏度估计对信号的稀疏度做一个预测。将获得稀疏度代入gOMP算法当中。算法主要包括三个部分:稀疏度估计计算,确定迭代步长选取子原子,信号残差的更新。 为了便于对算法进行阐述,下面是对算法用到的符号的解释,如表1和程序1所示。 表1 SAgOMP算法流程符号说明 程序1 SAgOMP算法流程符号说明 输入:M×N的传感矩阵A,N×1维的观测向量y 输出:信号稀疏表示系数估计θˆ。 (1)初始化r0=y,Λ0=∅,A0=∅,t=1; (3)如果norm( A ,u(L ) ,2) (4)将S=K0/3求整,若K0小于3则默认S取1。 (6)令 Λt=Λt-1∪{J0}, At=At-1∪α(jfor all j ∈J0); (7)求 y=Atθt的最小二乘解: (9)t=t+1,如果t≤K则返回步骤5,否则停止迭代进入第10步; (10)重构所得θˆ在Λt有非零项,其值分别为最后一次迭代所得θt。 第(1)~(3)步为稀疏度估计部分,得到初始的估计稀疏度。第(4)步设置每次选择的原子个数,后面仿真实验会说明。第(5)到(9)步是广义正交匹配追踪算法过程。第(10)步输出。 在稀疏信号自适应迭代算法中,每次选择的原子个数L直接影响到算法的重构精度和运算速度。在SAMP中通过不停的修正L的大小来提高重构精度,则导致其计算量也很大。既然得到了估计稀疏度,那我们为什么不直接选择与重构速度快的算法相结合。在OMP中每次选取S次原子,来提高运算速度。所以本文借鉴[11]中的命题1: 命题1中符号“<>”表示计算内积;δK表示上述策略中使用到的估计参数;K0表示信号稀疏度的估计值K表示稀疏度的真实值。uK0表示与测量值y最相关的原子索引集合; 受命题1启发,我可以直接得到信号的估计稀疏度。但是如果直接将稀疏度代入gOMP中,随着稀疏度的增大,选择固定的K0势必会影响算法的迭代速度。为此本分使用了步骤(4)的方法。通过除法,稀释稀疏度增大会选取步长产生的影响。 为了验证gAOMP算法在不用提前知道信号稀疏度的条件下的重构概率,测量次数和算法平均运行时间等方面的性能。,在MATLAB 2015b仿真平台上对经典的OMP算法,ROMP算法,CoSaMP算法,StOMP算法,SAMP算法,gOMP算法与本文提出的gAOMP算法进行对比实验,硬件环境为PC:Intel Core i3-2370M CPU@2.4GHz,4G内存。仿真实验中参数的设置如下: 测量矩阵 A:M×N(256×512)的高斯随机矩阵作为仿真实验的测量矩阵。 信号源:假设信号x是N×1维信号, 迭代终止条件:当残差‖‖r2小于le-6算法停止迭代,或达到预设的迭代次数,算法重构失败。 重构成功认定的标准:‖‖x-x˜2 为了在gOMP算法中选取合适的S,改良gOMP算法。本实验对重构精度和k(S=K0/k,k是我们选择的系数)对不同稀疏度进行了仿真。得到不同稀疏度下,k值对重构概率的影响。 图2 不同稀疏度下,k值对重构概率的影响 由图2可知,当取值k=3,4,5,6,7时重构概率基本一样。这是因为当k越大,则步长越小。通过最小二乘法进行运算时,每次选取的系数匹配度更高,则结果更精确。现在为了确保精度并兼顾运算速度,每个取尽可能多的原子数进行迭代。本文选择了k=3,因为在此基础上提升k值,重构准确率的提升已经不明显了,所以提高每次选择的原子数,进一步提高运算速度。 这一部分比较了 OMP,ROMP,StOMP,CoSaMP,SAMP,gOMP,SAgOMP算法的性能。SAMP中的步长取 5。 δKϵ(0 ,1)的取值影响稀疏度估计中对K0影响,过小则预测的稀疏度过低,过大则稀疏度过高。本文取极限0;在RIP中,取极限当δ=0时,RIP的不等式实际上表示的是观测所得向量y的能量等于信号x的能量,在线性代数中所讲的正交变换也具有这种性质,也称为等距变换。当然这里的变换因为传感矩阵A不可能是正交矩阵(不是方阵)所以得到的稀疏度肯定是小于实际的稀疏度。 图3 不同恢复算法的不同稀疏度下的重构概率 由图2可知,在重构精度上,重构所需的SAgOMP算法的重构精度比SAMP低比gOMP高,且gOMP需要知道信号的稀疏程度。相比其他算法在重构精度上毫不逊色。在SAMP中由于在选择原子迭代时会做进一步修正,使得重构精度更高。我们也可以很容易得出另一个结论,如果一个算法的重构精度越高,则它在达到精确重构是所需的样本越少,具体仿真笔者也做了,如上所言。在以后将CS运用到实际通信当中,就可以在满足足够的重构精度下,尽量减少样本数据的选取。进一步提高重构速度,提高应用价值。 图3 不同稀疏度下,不同算法与所需重构时间 如图3所示,随着稀疏度K的增大,各算法的平均运行时间相都在呈上升趋势。SAMP从图可知对SAMP(S=5)而言随着稀疏度的增加重构时间有指数增长的趋势,而本算法的运算速度增加幅度小,而且当K值增大时,本算法的平均用时增长速度远小于SAMP。相对其他算法,本算法可以对信号的稀疏度进行估计。进一步提高了实用价值。综合以上实验结果,SAgOMP即保留了SAMP中较高的重构精度,而且也保持了gOMP较快的运算速度。且稀疏度自适应。大大提高了本算法实用价值。 为了进一步提高压缩感知重构算法的实用性,本文在gOMP的基础上增加了稀疏度估计,并修改了gOMP中每次选取原子S的选取。仿真结果表明,在微小的牺牲SAMP算法重构精度的条件下,大大降低了算法的平均运行时间。对基于压缩感知使用实践也是一种有用的重构算法。今后的目标是将本算法进一步应用到MassiveMIMO信道估计当中。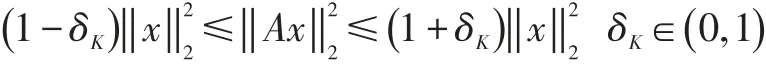
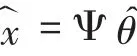
2 稀疏度自适应的广义正交匹配重构算法
2.1 SAgOMP算法流程
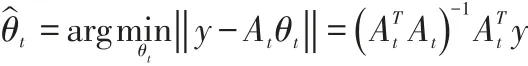
2.2 稀疏度估计计算
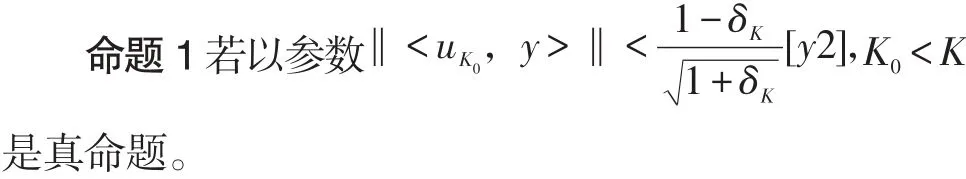
3 仿真结果与实验分析
3.1 实验设置
3.2 步长L的选取
3.3 重构成功概率分析

3.4 平均运算时间和稀疏度分析
4 结语

