基于马尔可夫链的RESTful服务可靠性评估优化
江金莲,关婷婷
(上海海事大学信息工程学院,上海 201804)
0 引言
软件测试作为预测软件质量好坏的关键一环,在整个软件生命周期中扮演着重要的角色[1]。软件测试是为了发现软件错误和执行程序的过程,提高测试效益,可以更好发挥软件测试的效果。软件统计测试通过对输入统计分布进行分析生成测试用例,可以通过软件统计测试达到分析软件质量目的,并且提高软件测试的安全性和可靠性的性价比[2]。为了保障软件测试的充分性,优化软件测试方法,加速软件测试,对于高质量可靠性软件,一些关键操作的使用概率较小,在测试过程中由于测试充分性不足,会导致严重的后果。针对该特性,提高关键性操作的权重,获取软件可靠性的无偏估计,利用重要抽样方法选择适合的抽样分布,近似精确估计,从而达到软件高可靠性要求[3]。
本文在保证软件可靠性无偏估计的情况下,使用马尔可夫链模型描述软件使用过程,提高对模拟结果有重要贡献的部分的概率,从而提高测试的充分性。利用启发式遗传算法迭代种群进行马尔可夫链矩阵概率优化,提高关键操作转移概率,加速软件统计测试效率[4]。本文主要研究工作主要是:在保证软件可靠性无偏估计的情况下,依据重要抽样方法,选择合适分布概率,利用遗传算法适度函数,选择个体,交叉并引入内外部变异,最终得到转移矩阵的最优解与最小方差,本文最后仿真实验模拟对比了模拟退火算法和标准统计方式,得出在可靠性无偏估计的情况下,关键操作执行次数的增加,增强了软件服务质量的效率。
1 RESTful服务设计和实现
1.1 RESTful服务背景
RESTful服务将一切视为资源,资源的表现形式则是RESTful的表现层,客户端和服务器之间传递的HTTP请求就是资源的表现层[6]。为了模拟用户浏览器的请求行为,通过调用HTTPClient工具包进行模拟浏览器发送post请求,指定URL,调用setEntity方法设置请求参数,execute方法执行请求,最后调用HTTPRe⁃sponse的getHeaders方法获取服务器的响应头信息,getEntity方法获取服务器的响应内容。设计apiRe⁃quest请求类,客户端通过 get、post、put、delete 等多httpType类型方式操作服务器,实现服务器的状态转换,由于状态转换是建立在表现层,则为表现层状态转换。
1.2 RESTful服务转移概率矩阵
在RESTful服务上编写A、B、C等资源,对资源内部进行操作,例如对资源 A 进行 get、post、delete、up⁃date、put和option操作属于资源A的内部操作;利用RESTful服务的过滤器,可以统计到资源A、B、C等在整个RESTful服务的使用中资源之间的转移概率矩阵。在资源内部的操作仍旧属于资源A,由此统计出资源A的失效概率,且资源之间的操作路径中任一资源的内部操作失效,则认为此次资源路径失效,因此本文研究RESTful服务的可靠性不仅保证了资源本身的可靠,更加从内部保证了资源操作的可靠性,保证了双重可靠。
2 马尔科夫链的软件可靠性
2.1 马尔可夫链背景
马尔可夫链是数学中具有马尔可夫性质的离散事件随机过程。该过程中在给定当前知识或信息情况下,过去对于预测将来是无关的[5]。P(Xi+1=x|X0,X1,…,Xi)=P(Xi+1=x|Xi)=公式显示出,i+1的状态只与状态i有关。软件测试的测试用例一般基于逻辑覆盖和基本路径生成,构成一个完成的测试试验样本控件,将测试用例的生成和发生概率和马尔可夫链模型联系起来。
2.2 马尔可夫链使用模型
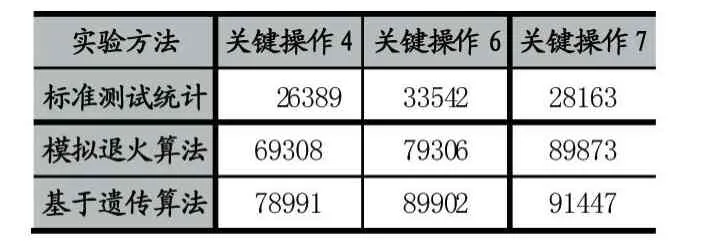
马尔可夫链软件测试使用模型,初始状态1表示软件使用开始和终止状态n表示软件使用结束。通常我们利用强有向图G=(V,A)表示,其中V表示各个状态V={1,2,…,n},A表示状态之间的边,转义概率表示从状态i转移到状态j的概率,Markov有初始转移概率矩阵[7]。用n×n的矩阵P表示迁移矩阵概率,用 pij表示从状态i转移到状态j的概率,用 pij表示,且 pij必须满足:0 软件在一次使用过程中发生失效用函数Cf(x)表示,Cf(x)=1表示路径x执行过程中操作导致软件失效,否则Cf(x)=0,因此Cf(X)的算术平均就是软件失效概率的无偏估计,EP(Cf(X))是失效概率的数学期望,用β表示。软件在一次使用过程中完成规定功能的概率称为软件可靠性定义,本文此处将软件可靠性表示为D,因此软件的可靠性为D=1-EP(Cf(X))。 重要抽样方法是在保持样本期望值不变的情况下,改变现有样本空间的概率分布将方差减小,增加贡献大的抽样出现概率,使抽样点更有效,以达到减少运算时间,本文利用重要抽样在保证软件测试可靠性的情况下,加速了软件测试速度[8]。 假设关于随机变量X的概率密度函数为f(x),求软件失效概率的数学期望β,即: 可得重要抽样分布函数与随机变量X的期望相同,即重要抽样的失效概率无偏估计是随机变量X的失效概率无偏估计。R(x)称为重要抽样权函数,亦可以称为似然率,R(x)=f(x)/h(x)。其中 h(x)为重要抽样分布密度函数。失效概率的无偏估计: 校验无偏估计公式为: 可以得出,计算方差的公式为: 因此,可以得出结论Var(β)最小的函数即为最优矩阵函数。在保证失效概率无偏估计的情况下,方差越小,软件可靠性越稳定,统计测试花费开销越小。 本文研究对象是针对RESTful服务构建的马尔科夫链转移概率矩阵,基于上述公式论证可以得出软件质量服务的可靠性是基于转移概率矩阵的方差必要条件,如何选择出最优矩阵是可靠性评估的核心问题所在。 在仿真求解最优方差矩阵过程中,需要选择合适的测试路径。一条好的测试路径不仅能够找到所有可能的埋点,而且能够对低执行概率关键操作做到一定的覆盖。本文依据当前的最优转移概率矩阵,基于当前的操作状态作为起始态,提出利用随机投掷统计概率方法选择下一个操作状态,直至最终的操作末态,一条测试路径选择终止。随机投掷统计概率方法如下: (1)依据当前转移概率矩阵行各个操作的执行概率,建立坐标轴概率分布。 (2)生成随机投掷数random(0,1),记录散落在坐标轴位置属于相应操作点,并记数累加。 (3)循环执行一定次数n,统计得到n次的各个操作落入的点数。 (4)统计各个操作的落入点数占比,选择占比率大于自身转移概率的操作,作为下一个转移操作状态。 (5)重复递归选择,直至选择操作状态为末态操作。 遗传算法思想源于适者生存的自然界动物生存规律和生物遗传学,遗传算法通过模拟达尔文生物进化论中遗传算子的组合交叉和变异产生出新的种群解集,通过基因进化过程,搜索最优解[9]。通过重要抽样法的分析可知,在保障可靠性的情况下,得到统计测试加速的关键在于求得失效概率方差最小的矩阵,可以减少工作量和保证测试的充分性。本文通过比较个体方差得到最优解,将遗传算法和重要抽样结合,利用遗传算法搜索最优解,算法描述如下: 输入参数:使用Markov的概率迁移矩阵,关键操纵的集合S,事先确定的每个操作的失效概率; 输出参数:优化随机矩阵Q。 重要抽样和仿真过程: (1)在遗传算法每次产生变异体之后进行随机生成N条测试路径; (2)初始化路径Xi,遍历Xi中每一个操作,若ran⁃dom(0,1)小于对应操作失效概率,则路径Xi的失效概率函数Cf(Xi)=1; (3)失效概率方差计算公式: 遗传算法与重要抽样结合算法过程: (1)随机生成M个个初始种群即M个矩阵,以及矩阵Q为n×n的0矩阵,其中关键操作的概率不得小于初始矩阵P中的概率,M个个体生成的矩阵必须与pij=0和 pij=1保持一致且必须满足markov软件模型 (2)根据场景这里确定适度函数为矩阵失效概率方差,初始值为设置为无穷大,记为varmin=9999(表示无穷大),优化矩阵初始化Q=P; (3)根据轮盘赌选择方法,先计算出个体个体在总体个体适应度中的概率,然后计算出个体的累计概率,random()随机生成一个[0,1]之间的数,该数在哪个个体的累计概率中,则选择哪个个体,因此选取两个矩阵最为交叉个体; (4)交叉选择的两个矩阵,因为矩阵是多行多列,此处选择k-opt交换方法,根据k-opt方法直接将两个矩阵A和B内部的几行进行交换,本文利用矩阵长度:index 1=random.randint(0,len(A)),index2=random.rand⁃int(0,len(A))得到A需要与B交换的几行,将A的[in⁃dex1:index2]与B[index1:index2]的进行互换; (6)利用重要抽样将变异之后的矩阵进行重要抽样,随机抽样出N条测试路径,并且进行路径失效仿真,得软件失效概率方差,若小于varmin,则将新值替换varmin,并且将其赋值给Q; (7)若是孕育发生新的个体数达到M个,则将产生新一轮的群体替代老群体; (8)当新群体代数达到T终止循环,得到失效概率最小矩阵Q,输出。 图1 遗传算法流程图 基于遗传算法的软件可靠性重要抽样,利用本文已经实现的软件说明。RESTful服务总共包含8个资源,初始状态为1,终止状态为8,(3,4),(4,6)和(6,7)导致关键操作为4,6,7。各个资源失效概率(0,0.001,0.001,0.001,0.001,0.0001,0.001,0.001,0.0001)。依据服务历史统计数据分析,构建初始Markov转移概率矩阵如下: [0,1,0,0,0,0,0,0], [0,0,0.85,0,0,0,0,0.15], [0,0.09,0,0.03,0,0.1,0,0.78], [0,0,0.29,0,0.37,0.03,0.15,0.16], [0,0,0,1,0,0,0,0], [0,0,0.6,0,0.18,0.19,0.03,0], [0,0,0,0,1,0,0,0], [0,0,0,0,0,0,0,1]] 本文根据模拟退火算法和遗传算法以及标准统计测试分别抽样1000条测试路径仿真100次,得到软件操作执行次数测试实验结果如表1所示: 表1 仿真关键操作执行次数对比 从上述100次仿真结果可以看出,基于标准统计测试,模拟退火算法和遗传算法都能很好地使关键操作4,6,7得到充分测试,遗传算法较大地提高了关键操作的执行次数,增大了关键操作的执行概率。根据模拟退火算法和遗传算法以及标准统计测试分别抽样1000条测试路径仿真100次,得到方差实验结果如表2所示: 表2 平均方差对比 从上述100次仿真结果可以看出,基于标准统计测试,优化矩阵的方差为3.5×10-2;基于模拟退火算法优化矩阵的方差为2.43×10-3;基于遗传算法优化矩阵的方差为1.44×10-5;显然,遗传算法比模拟退火算法能更好地降低估计方差。 在100次仿真中,每次仿真遍历路径1000条,每次仿真得到100个最优矩阵和最优方差,遗传算法与模拟退火算法相比,执行次数更加充分;针对方差方面,模拟退火相比基本统计测试失效概率方差更小,统计测试开销花费较少。因此,遗传算法不仅保障了软件测试可靠性,且相比于模拟退火使得关键操作的测试更加充分,使得加速统计测试得到更好体现。 本文通过将遗传算法和重要抽样结合,得到一种新的软件统计测试的加速方法,在保障RESTful服务的软件测试可靠性的前提下,提高了关键操作的概率,保证了测试充分性。基于RESTful服务资源的可靠性,且与已有的模拟退火算法作比较,与模拟退火算法相比,本文提出的遗传算法具有更优性。但是遗传算法求失效概率方差最小的矩阵Q时,需要记录仿真中间输出结果需要花费一定的性能损耗代价,并且无法得到最优解,只能在有限的仿真次数范围内尽可能得到可靠性无偏估计的近似最优解。但是也发挥了重要抽样的优点,降低了方差,使得关键步骤操作概率增加提高测试效率和速度,加速了软件测试,并且通过仿真实验结果证明了此方法的有效性。
2.3 软件可靠性估计
3 基于重要抽样统计测试设计
3.1 重要抽样方法度量



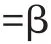

3.2 测试路径选择度量
4 重要抽样遗传算法的设计实现


5 实验结果与分析
5.1 RESTful服务实例
5.2 仿真结果对比

6 结语

