短跑运动一般规律与测试图线新绘法

董俊道



短跑运动一般规律与测试图线新绘法

董俊道

（哈尔滨理工大学应用科学学院，黑龙江 哈尔滨 150080）

目前只量化了短跑运动员类弹性属性，给出最优秀短跑运动员测试图线的近似解法。对比速度图线，量化精神层面生物特性的影响，直观地认识到外力作用于人体，既损失在生物特性上，又改变人体的运动状态。研究确定短跑中人体纵轴的方法，不仅量化人体的转动状态，还可求出人体的转动半径，确定短跑中人体重心的位置。从而冲破层层难关，给出简单可行绘制短跑测试图线的全新方法。使绘制测试图线进入常态、全面解析短跑运动、编制短跑运动智能诊断和指导软件成为可能。

短跑；精神层面生物特性；通用解法；测试图线新绘法

20世纪五六十年代，由于经典力学取得巨大成功，众多力学家开始用经典力学模型解析人体的竞技运动，结果误差较大[1]。近几十年，人们用力学知识研制了许多测试人体运动的装备和技术，认识到经典力学对人体运动起主导作用，中外运动生物力学专家普遍认为人体竞技运动应遵循经典力学规律。参考大量中外文献编写的运动生物力学教材表明，当今世界潮流坚持片面地运用经典力学分析人体运动。文献[2-4]中的形势，阻碍了对人体运动中生物特性的探索和运动生物力学的发展。而人体并非刚体，人体运动中必然表现出生物特性。本文依文献法进一步探究短跑运动中精神层面生物特性的影响。通过比较两种测试图线说明“积极摆动”思想产生僵化运动，致使着地过程受到较大阻力[5-6]。

对比速度图线得知，速度图线与上部水平线间的面积可量化生物特性导致的损耗，速度图线及其下部反映人体的运动参量，进而给出短跑平面运动的通用解析式。探究确定人体纵轴的方法，通过力学运算给出短跑运动中任意瞬间的转动半径，从而克服了用惯性参数法绘制短跑测试图线需要采集大量数据、用一系列回归方程进行大量运算，甚至涉及人体隐私部位遮挡部位等的测量、肢体变形后环节识别点变位等诸多难题。给出绘制位移、速度图线、有效力图线、角速度图线等的方法。为全面解析短跑运动创造条件，为编制短跑运动智能比较、诊断软件开辟可行之路。

1 对比两种速度图线

图1为比较图线，图中点左侧上部是“丘巴”资料[7]提供短跑测试图线之前支撑时段水平速度图线（用#号代表）。其下面是文献[5]短跑水平速度图线之前支撑时段的速度图线（用&号代表）。#号速度图线为当时世界上最优秀短跑运动员的速度图线。&号速度图线为我国短跑健将级运动员的速度图线。对应“积极摆动”思想指导的短跑运动员。

两图线经过适度放大，使两图线始点终点接近重合，从而便于比较。①比较速度图线时，应与优秀运动员的速度图线比较，这样比较容易看出差在哪。比较发现优秀短跑运动员着地缓冲技术非常好，着地过程动能损失的位移等于#号速度图线与其上部水平线包围的面积，其损失占比最小[8-9]。②精神层面指导思想使运动员着地时一些肌肉处于僵化状态致位移损失较大。参赛运动员紧张时也会产生僵化现象，僵化现象也是一种常见的生物特性。图1表明，短跑中这种生物特性也可量化，#号速度图线与&号速度图线间夹的面积等于这种生物特性损失的位移。③对比#号速度图线与&号速度图线发现，文献[10]提供的解析方法只给出解析最简单短跑水平速度图线（没有精神层面生物特性参与的速度图线）的方法。

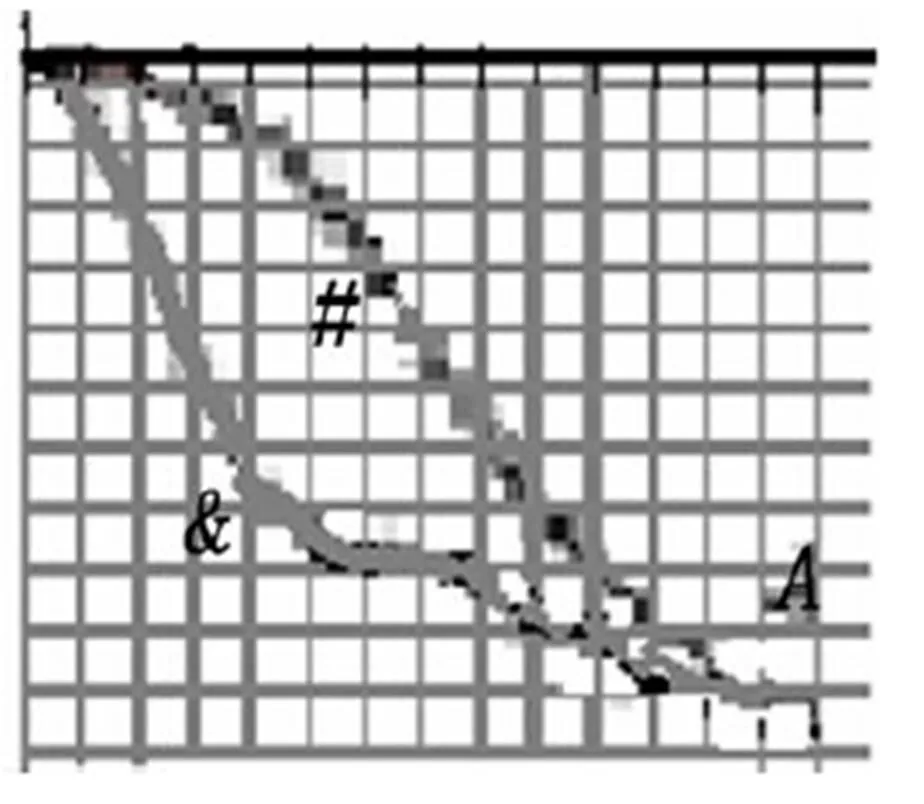
图1 比较图线

2 短跑水平运动的一般规律

体育界最需要的是解析短跑水平速度图线的一般规律。速度图线通用解析法如图2所示。

研究短跑运动主要从侧面观测其支撑时段的水平运动，这个侧面称为平面。运动员沿轴前进，向上的轴代表竖直方向。

图2中示意给出两条曲线，顺次为某运动员途中跑支撑时段实测水平摩擦力——时间图线（图线）及用惯性参数法绘制的水平视速度——时间图线（图线）。从力学角度研究短跑时，以水平摩擦力图线中部摩擦力等于0瞬间为前、后支撑时段分界点。

示意给出短跑的速度时间图线原因为：①文献[7]与文献[5]都没有考虑空气阻力，文献[7]给出的支撑时段竖直位移图线及水平速度图线都是用惯性参数法绘制的，它们的始、终点都在一个水平线上。表明运动员着地与蹬离瞬间重心的水平高度相同，运动员重心的初末水平速度相同（都等于腾空时的水平速度）。而文献[5]给出的位移图线及速度图线的后部明显上翘[6]，不知道这种速度图线上缘是斜线还是弧线。②在网上输入“短跑速度图线”搜索，或搜索相关论文没得到任何信息，目前能查到实测绘出的图线太少。

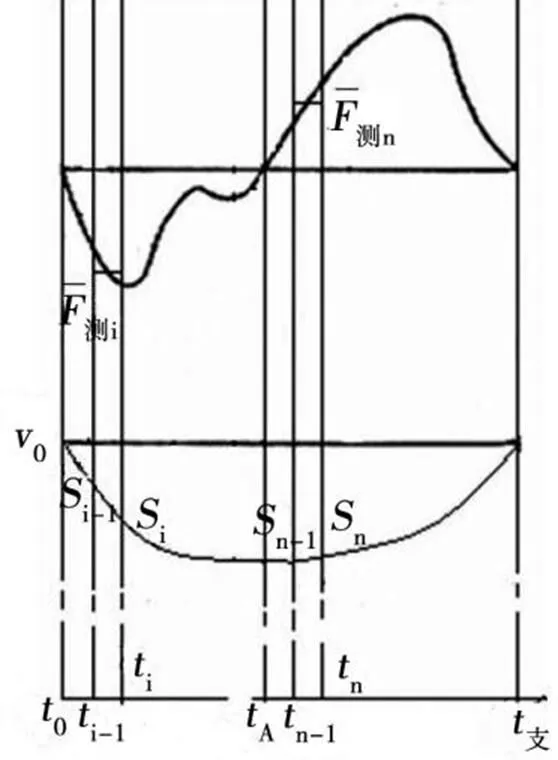
图2 速度图线通用解析法

2.1 短跑前支撑时段运动规律

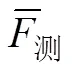
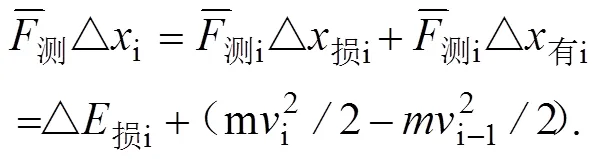
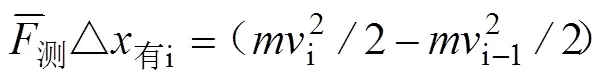
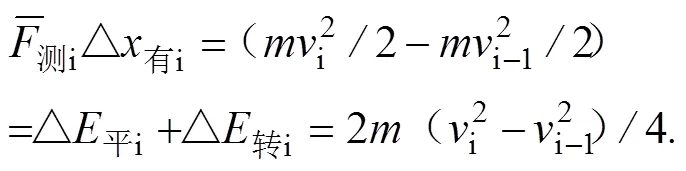
2.2 短跑后支撑时段运动规律

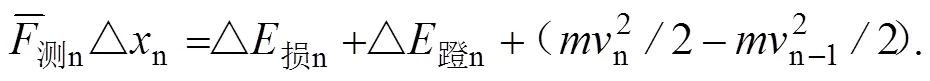
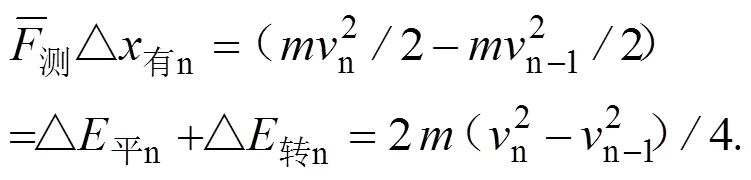
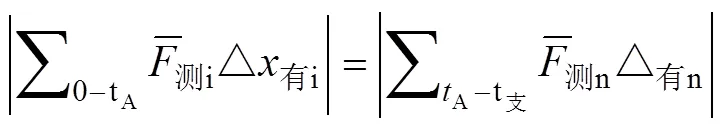
2.3 相关联想

2.3.1 前后支撑速度图线上部面积涵义不同

前支撑时段速度图线上部各段小位移之和等于前支撑时段损失的总位移。后支撑时段速度图线上部各小段位移之和等于后支撑时段补偿的总位移。故后支撑速度图线上部各小段位移表示该小段△损n与△蹬n共同作用补偿的位移。两个生物维度维度补偿结果表明△损n＜△蹬n.

2.3.2 代表平动刚体质点的速度图线是一维速度图线

用一重积分或一重累加式可以解析。想全面解析短跑的速度图线，需要多重累加式，因为它们是多维速度图线[8-10]。文献[5]直接用水平力递推，是将速度图线视为一维图线，无视其中损耗，致使递推的前支撑速度图线下沉，后支撑速度图线尾部上翘。

2.3.3 解析短跑运动的充要条件

式（1）与式（3）给出解析短跑运动的充要条件：既要考虑运动员的生物特性（充分条件），又要考虑将人体视为刚体时遵循的力学规律（必要条件）。

2.3.4 视速度是假设人体为刚体时的视速度

文献[10]一开始指出的视速度，其实不是真实的视速度，而是假设人体为刚体时的视速度。另外其中式（3）下面的分析式左侧少个“”。文献[10]是实验数据处理的一种成功的近似方法，其适用范围是运动中涉及的各维度都是机械运动维度。

3 人体的纵轴及着地瞬时重心的位置

短跑测试图线中最难绘的是依惯性参数绘制竖直位移图线与水平视速度图线。文献[5]用德国技术，通过实测摩擦力直接递推位移、速度，绘制出我国第一组短跑测试图线。由于这种绘法未考虑人体的生物特性，所以绘制的位移图线、速度图线误差较大。

在网络技术高度发展的今天，这一事件折射出外国对短跑测试图线的绘制仍处于探索阶段。前几年赵焕彬博导曾带领研究生探索环节点自动识别技术试图攻克用惯性参数绘制位移、速度图线的难题。但没有自己绘制的正确图线，只分析两种文献提供的短跑测试图线，作用很有限。无法深入认识短跑运动的规律，也就无法通过测试图线的比较，对我国短跑运动员进行全面准确的诊断、指导。为改变这种形势，我们探讨并确定走跑运动人体纵轴的方法。

文献[2]阐述环节惯性参数中德国研究结果表明，各环节的重心沿着环节纵轴分布。当人竖直站立时，其头部重心在两耳上缘连线与正中面交点，头部重心记作头.测试某短跑运动员时，用高速摄像机拍摄运动员的影像，得到系列影像。对每帧影像资料依上法通过计算机三维技术给出人体头部重心头的准确位置。

走跑运动中人体靠内力作用实现各环节的左右对称摆动时，腿脚部总重心应与纵轴重合。考虑腿脚各环节的端点较易识别，所以通过腿脚的6个回归方程推算出腿脚部分重心再与两只鞋的重心合成腿脚总重心头腿脚.通过计算机给出头腿脚连线，延长其与头顶面的交点为顶.任意瞬间这样的线段顶i腿脚i为支撑时段对应瞬时运动员的纵轴。将纵轴投影到平面上。用计算机三维技术推测得出对应瞬间纵轴前倾角为i，=0，1，2，….

短跑运动中视速度的波动量与腾空时水平视速度之比为2%左右。运动员角冲量波动量与着地瞬间的角冲量之比与其相同[8-9]。运动员的位移、速度图线可以精准地给出。当下可以对短跑运动进行精准测量的情况下，应能精准地确定人体短跑运动的系列纵轴。

开始绘制竖直位移—时间图线、水平视速度—时间图线时，可用塑形盘结合称量法推算出着地瞬间运动员重心的位置。塑形盘为一透明长方盘，上侧有可移动固定头、手、腰、腿、脚等的滑块（滑块上部有海绵垫）。下侧有可平行移动的天、地槽及显示纵轴的激光器。首先依着地瞬间运动员的影像及着地角在塑形盘上准确塑形固定运动员。着地脚鞋底处下面的地槽BD（可视为线段）代表地面；塑形盘头顶处下面有始终与地槽平行的天槽LK（可视为线段）；天地槽间距等于着地瞬间运动员的高度.天、地槽下方分别用约10 cm长的三棱柱支撑，而三棱柱分别放在电子称上衡量。准确调整两个三棱柱的位置，不但要平行地放入天、地槽中，而且要保证塑形盘水平。读取两电子秤的测量值，用计算机除去塑料盘等重量的影响，即可给出运动员重心所在的位置CP。依前面叙述的方法给出运动员纵轴并用激光器显示出其在平面的投影，即知运动员刚着地时纵轴与轴的夹角0.CP与BD、LK平行。CP与BD距离等于重心高度。也等于对应瞬间支撑半径的竖直分量0.CP与纵轴的交点为运动员着地瞬间重心的具体位置。此测量法原理源自文献[4]，此装备有待研制。

因为人体不同环节拍摄的视角不同，运动员还有绕前后轴、竖直轴地摆动。对短跑不同平面上的运动，要用对应的纵轴投影进行解析。

4 短跑平面运动的滚动半径与短跑中的重心

还可从支点处（地面）观察短跑的平面运动。将无摩擦滚动的运动员视为刚体时，任意时段对地有：

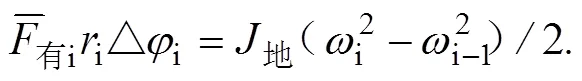
其中△ii=△有i，i为转动半径，等于支撑半径的竖直分量。刚体的转动，不论从刚体重心角度看，还是从地面看，转动半径、转动角度及角速度都相同。

以支撑半径下端为转轴时依平行轴定理有：

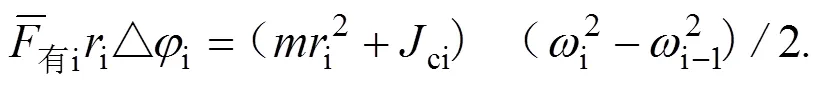
由式（2）知：

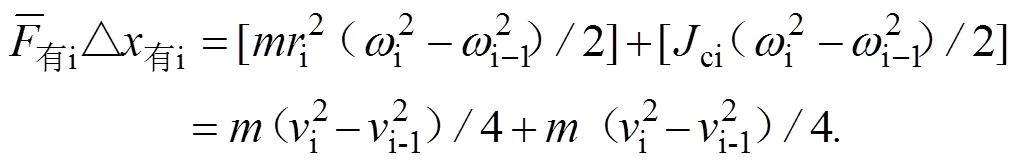
不难推出短跑支撑时段第段运动员对过其重心左右轴的转动惯量：

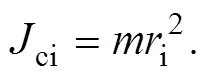
公式（7）极大地简化了运动员对通过其重心左右轴转动惯量ci的计算。参阅文献[8-9]中动能定理关系式与对应动量定理关系式的转换，依式（6）可推出其对应的动量矩定理表达式为：

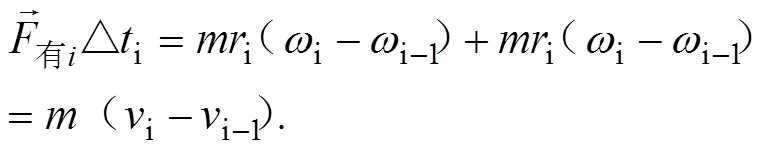
于是：

i可求。给出i时刻人体转动半径i，可知对应瞬间运动员重心位置。也就是说，确定了短跑某支撑时段运动员的纵轴，也就能确定短跑某支撑时段运动员的重心。这时还应进行的工作是将新求出的半径与运动员的身高进行比较，看有无相应的规律。由于后支撑时段有效力的功能关系式（4）与式（2）相同，所以式（9）亦适用于后支撑时段滚动半径的推导。

5 绘制短跑测试图线的新法

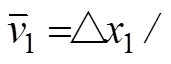
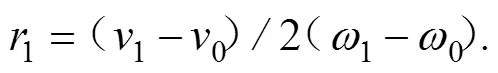
由式（9）知：

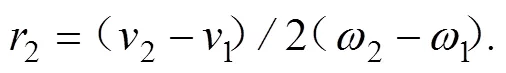
对任意小段有：

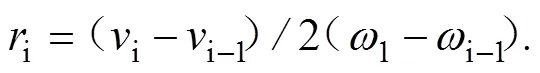
竖直位移—时间图线i秒末重心的坐标（i，i）；水平视速度—时间图线i秒末坐标（i，i）。还可求出重心竖直速度图线、有效力图线、角速度图线等对应的i秒末坐标。

6 讨论

根据上面的方法进行如下讨论：①文献[5]反映，目前世界上正在探索短跑测试图线的绘制方法。文献[5]的功绩在于给出我国第一组短跑测试图线，虽然有争议，但它使我国在这方面迈出第一步的事实不可否定。进而才有文献[6]与本文图1短跑速度图线的比较和后面那些更深入的认知。②依据短跑运动是肢体左右摆动交替支撑的无滑动滚动及短跑参量的波动，判别短跑中运动员纵轴也存在波动，给出确定纵轴的方法和相关分析，从而给出短跑位移、速度图线的全新绘制方法。这是进一步探索的具体方案，但塑形装置及相关的计算机软件等有待研制，进一步实施、检验尚需一段时间。③文献[5]提出的方法可以在德国试用，可以在中国试用，那么我们提出的方法也可直接试用。直接试用也能进行全面检验，如试测后绘制出的位移、速度图线不沉、不翘，说明我们的方法更科学。④合成人体腿脚部分重心时，用哪国的环节参数都行。推算出总重心的位置可能不同，但都分布在纵轴上。因为人们走跑时遵循的力学规律相同，主要看环节参数是否容易识别。用各国的惯性参数推断纵轴，也是一种检验方法。⑤运动员塑形固定后还可进行X光摄影，然后用计算机三维技术推得系列三维影像资料，可准确确定系列的纵轴。可用于对比、校正不同方法确定的纵轴，或择优录用。生物体是个非常复杂的系统，对其整体运动规律的认识只能步步为营，不能一蹴而就。

7 研究结论

经过研究，得到如下结论：①目前世界上仍认为人体运动完全遵循经典力学规律，导致现阶段多种文献对竞技运动的分析停留在经典力学分析的层面，阻碍了运动生物力学的发展。②对比速度图线发现外力作用于人体的一般规律，即式（1）（3）表述的规律。该规律诠释了解析短跑运动的充要条件为外力功既要消耗在生物特性上，又要改变人体机械运动状态。③剥离生物特性后，前后支撑时段人体都可视为做无滑动滚动的刚体。④给出各维度对应的力学微元与直观的微积分方法是解析短跑运动的重要保证。⑤给出运动员纵轴，就能给出运动员的重心。方可用全新方法绘制短跑的竖直位移图线、短跑的水平视速度图线。不但极大地简化了绘制短跑测试图线的方法，还使更全面认识人体的运动成为可能，也使绘制短跑图线常态化、全面解析短跑运动成为可能。⑥必须从物理角度研究生物体运动的基本形式、基本概念、基本规律、运动维度；必须引入多维度力学微元，才能深入认识竞技运动的力学特征、生物特性和相关力学规律。生物物理学是研究生物体运动的基础科学，是实验性基础科学，必须依赖对竞技运动的大量观测。人体的竞技运动貌似一般的机械运动，实际上是生物类运动、生物性动力源与刚体的复合运动，是非常复杂的运动。必须通过实测绘制出各种图线才能进行分析，也就是说人体的运动规律隐含在其测试图线里。不论是研究竞技运动的规律，还是诊断指导，都离不开对测试图线的分析。如果不对测试图线分析，就不能形成完整系统正确的认知，所以迫切需要简单易行的绘制方法。

［1］运动生物力学分会.运动生物力学学科发展研究报告［R］.北京：中国体育科学学会，2007.

［2］赵焕斌，李建设.运动生物力学［M］.北京：高等教育出版社，2015.

［3］陆爱云.运动生物力学［M］.北京：人民体育出版社，2015.

［4］全国体育教材编委会.运动生物力学［M］.北京：人民体育出版社，2005.

［5］施宝兴.短跑支撑阶段运动生物力学分析［J］.体育科研，2010（31），06：40-43.

［6］董俊道.对比两种短跑测试图线受地启发［J］.中国科技信息，2018（581），08：35-37.

［7］文超.田径运动高级教程［M］.北京：人民体育出版社，2005.

［8］董俊道.检验短跑前支撑平面运动是三维运动的方法［J］.中国科技信息，2018（579），07：75-77.

［9］董俊道.短跑后支撑速度图线的解析［J］.中国科技信息，2018（580），08：33-36.

［10］董俊道.短跑运动的生物特性及适用规律［J］.中国科技信息，2018（578），03：62-65.

［11］董俊道.“小步，高频”竞走技法及相关力学规律［EB/OL］.［2012-11-07］.http：//www.paper.edu.cn/ releasepaper/content/201211-101.

〔编辑：严丽琴〕

2095－6835（2018）19－0033－05

G822.1

A

10.15913/j.cnki.kjycx.2018.19.033