考虑运动副间隙的机构动态特性研究
薄少军 牛胜涛
摘 要: 为了研究运动副间隙对机构动态特性的影响,基于“连续接触”模型,建立改进的非线性接触碰撞模型。间隙处的摩擦用修正的库伦力摩擦模型描述,转动副之间的间隙用矢量杆等效。以内燃机曲柄滑块机构为例,在ADAMS中建立含间隙模型,采用接触碰撞函数的算法,定量分析间隙对机构动力学特性的影响,验证理论值与仿真结果的可靠性,为含间隙机构的分析、设计与寿命预测奠定理论基础。
关键词: 运动副间隙; 摩擦; ADAMS; 连续接触; 动态特性; 接触碰撞
中图分类号: TN03?34; TB567 文献标识码: A 文章编号: 1004?373X(2018)19?0155?06
Abstract: In order to study the influence of the joint clearance on mechanism dynamic characteristic, an improved nonlinear contact collision model is established on the basis of continuous contact model, the modified Coulomb force friction model is used to describe the friction force at clearance joints, and the revolute clearance joints can be equivalent with vector stick. Taking the slider?crank mechanism of internal combustion engine as an example, the model with clearance is established in ADAMS, and the algorithm of contract collision function is used to quantitatively analyze the influence of the joint clearance on mechanism dynamic characteristic. It is verified that the theoretical value and simulation result are reliable, which lays a theoretical foundation for the analysis, design and life prediction of the clearance mechanism.
Keywords: joint clearance; friction; ADAMS; continuous contact; dynamic characteristic; contact collision
0 引 言
在实际应用中,由于装配、加工误差和磨损,运动副中的间隙是不可避免的。间隙的存在破坏了理想机构模型,使机构的运动特性不能按照预期设计的轨迹进行,并随着运行过程中的摩擦和冲击载荷的作用,导致间隙变大,同时伴随有噪声和振动现象的出现,严重影响了系统载荷传递,甚至造成运动副的破坏和失效。
文献[1]采用概率分析的方法,研究了平面运动副间隙对机构动态特性的影响。文献[2]研究了滚针轴承有润滑作用时对机构特性的影响。文献[3]以涡旋压缩机机构为算例,把机构的间隙用非线性弹簧阻尼模型等效,研究了间隙数量和大小对机构平衡的影响,为提高涡旋压缩机的工作效率提供了理论参考。文献[4]基于间隙矢量模型,建立含间隙转动副的“碰撞铰”模型,研究了在高速驱动载荷下,间隙会使机构速度、加速度产生运动滞后效应,从动件呈现强烈冲击、波动现象间隙的存在,增加了系统的自由度。根据文献[5]振动测试实验结论,随着间隙值和驱动速度的增加,机构的振动与冲击情况呈现严重的非线性。文献[6]以解偶的四杆机构为算例,以不同的间隙值、驱动速度和阻尼为输入量,通过仿真,揭示了含间隙机构动力学存在明显的混沌现象。文献[7]从非线性动力学出发,验证了应用分叉和混沌理论研究非线性振动系统的必要性。文献[8]以六自由机构为模型,用数值分析的方法,从系统之间的能量转化观点解释了分叉混沌现象。
本文以曲柄滑块机构为研究对象,建立多间隙的机构数学模型,同时在动力学软件ADAMS中建立含间隙的动力学模型。基于改进的非线性接触碰撞力的混合模型,间隙处的摩擦用修正的库仑摩擦模型描述,进行仿真。通过数学理论推导和仿真结果,验证本文所建模型的正确性。
1 转动副
理想情况下不考虑间隙,销轴与轴套的中心是重合的。实际中运动副的间隙随着运动会产生磨损,造成销轴与轴套的中心发生偏移,相对运动构件之间会发生分离和接触。从分离到接触的过程中,当传动速度过快时,会发生剧烈碰撞,严重影响了机构的运转精度和平稳性。
目前对于转动副间隙的描述有三种假设:第一种认为销轴与轴套是一直保持接觸的,没有其他运动出现;第二种认为销轴与轴套处于分离与接触的循环中,接触时会出现碰撞力;第三种认为在一个运行周期中存在接触、分离和碰撞。考虑到机构的一般性,建立数学模型时采用第二种模型状态,接触构件分别用销轴与轴套表示,它们之间的间隙示意图如图1所示。图1中:[Ri] 表示轴套的半径;[Rj]表示销轴的半径。
由于间隙的存在,当相对运动的构件由分离状态过渡到接触状态时,在接触点之间发生碰撞,如图2所示。图2中:间隙矢量用[e]表示,[e]在[x]轴和[y]轴上的分量分别用[ex]和[ey]表示;[c]表示销轴和轴套的半径间隙,其值为[c=Ri-Rj];[ft]为切向的摩擦力;[fn]为法向的碰撞力;碰撞深度用[δ]表示,[δ=e-c]。

当[δ]值为零时,表示销轴和轴套刚好接触。在理想状态下,[δ=e-c=0]。当[δ>1.0×10-10]时,就认为发生相对运动的构件开始碰撞。
2 运动副间隙的接触碰撞力模型
根据文献[11]研究思想,间隙较接触碰撞模型的改进,是在弹性接触力基础上考虑某种形式阻尼力,结合接触碰撞力表达式,引入非线性刚度系数和Lankarani?Nikravesh模型刚度系数。
3 系统运动微分方程的建立
利用连续接触模型,转动副之间的间隙无质量杆代替,根据机构原理图知识,将曲柄滑块机构简化,如图3所示。
由式(8)可得:
由以上公式推导的各运动杆的位置、速度和加速度可知,从数学角度来看,构件的动态特性与间隙的大小、间隙角、初始速度有直接关系,要想确保输出机构的精确性,只需改变相关参数值大小,就可以实现机构的可控性。在含间隙的曲柄滑块机构中,构件在实际应用中由于间隙矢量和间隙角的变化具有随机性,不能准确地预测其变化范围,导致连杆和曲柄的传动性降低,偏离了初始设计机构的轨迹,降低了机械系统的精度。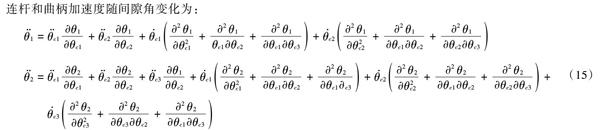
以上是基于“连续接触”模型,采用泰勒级数略去高阶无穷小项推导的理论公式。从理论来讲,对于含多间隙机构,曲柄和连杆的速度和加速度与间隙角有密切的联系。通过对输入量的控制,可实现对机构的动态特性的准确控制。
4 机构动态特性仿真分析
以S195柴油机的曲柄滑块为例,参照机器额定的各种参数如表1所示。在ADAMS/VIEW建立含间隙和理想状态的机构模型,假设曲柄和连杆,连杆与滑块之间存在间隙,设间隙大小为0.25 mm。无间隙时,在连接处添加运动副;考虑间隙时,相当于接触构件之间添加接触力,添加接触构件的一些物理参数,如刚度系数、阻尼系数、摩擦系数和恢复系数,采用IMPACT?FUCTION?BASED CONTACT的数值计算方法进行动力学仿真。
设定曲柄转速为1 200 r/min。为了消除初始状态对间隙机构动态特性的影响,仿真过程中,机构达到稳定状态后,以机构完成2个周期的加速度数据值作为分析对象。
1) 考虑连杆与滑块存在间隙时,其他运动副之间视为理想状态时,实线表示无间隙时的输出动态特性,虚线表示含间隙时机构的动态特性,如图4,图5所示。
2) 同时考虑连杆与滑块,连杆与曲柄之间的间隙时,机构的输出动态特性结果图如图6,图7所示。
由图4a)和图5a)可以看出,间隙对滑块的位置动态特性几乎没有影响;由图4b)和图5b)可知,在开始的0.08 s内,间隙对滑块速度有滞后作用;由图4c)和图5c)可知,滑块的加速度变化波动很大,间隙对滑块加速度非常敏感,导致连接构件之间碰撞力发生连续交变载荷,从而影响机构的稳定性。同时也验证了式(10),式(11)的正确性,间接说明了采用连续接触模型的适用性和可靠性。
由图6和图7可知,间隙对连杆角速度和角加速度都有明显的迟滞现象,且随着间隙个数增加,对连杆的动态特性敏感程度增加。根据式(14),式(15),理论上可以通过改变其中的参数实现对输出位置和速度准确控制,但在实际中,各种因子都是根据经验公式取得。所以要想实现对多间隙机构的精度控制,还需要一定阶段的研究。
从以上仿真结果和推导的理论公式可知,含间隙机构在一定程度上改变了系统的动力特性,使系统呈现高度非线性状态。随着间隙个数的增加,机构的稳定性越差,对机构的精确控制更加困难。
5 结 论
本文根据连续接触力模型建立含间隙的曲柄滑块机构,用非线性连续接触碰撞力的混合模型来描述接触构件之间的法向碰撞力,用修正的库仑摩擦力模型描述切向碰撞力。将其嵌入到动力学软件ADAMS中,结果如下:
1) 间隙使得机构的动态特性发生变化的主要原因具体为:间隙对位移几乎没有影响,在很短的时间内,对机构的速度和角速度有迟滞作用;对机构的角加速度最敏感,并且随着间隙的增多,比理想机构的波动要大得多,间隙的存在,增大了运动副之间的接触碰撞力,使机构呈现高频振荡的特点。
2) 含间隙机构的动力学特性真实地反映了实际机构的动态特性,能够准确地预测含间隙机构的动力学特性,为精确地研究机构精度和设计提供了基础。
3) 本文采用非线性连续接触碰撞力的混合模型正确地描述了含间隙机构的动态特性,且计算精度高,扩大了间隙铰接触碰撞动力学的应用范围,适合于实际工程应用。
参考文献
[1] 李玉娟.考虑运动副间隙的平面函数机构概率分析与综合[D].成都:西华大学,2015.
LI Yujuan. Probability analysis and synthesis of planar function mechanism considering motion pair clearance [D]. Chengdu: Xihua University, 2015.
[2] 耿德寧,郑长松,李春生,等.污染微粒对滚针轴承润滑影响规律理论研究[J].润滑与密封,2015,40(2):60?63.
GENG Dening, ZHENG Changsong, LI Chunsheng, et al. Theoretical research on the influence of pollution particles on the lubrication of needle bearings [J]. Lubrication and sealing, 2015, 40(2): 60?63
[3] 黄华军,张春,金鑫,等.含运动副间隙的涡旋压缩机动平衡仿真研究[J].振动与冲击,2016,35(5):125?130.
HUANG Huajun, ZHANG Chun, JIN Xin, et al. Simulation study on eddy compression dynamic equilibrium with clearance of moving pairs [J]. Vibration and impact, 2016, 35(5): 125?130.
[4] 张增磊,巫世晶,赵文强,等.含间隙高速多连杆传动机构动力学特性研究[J].振动与冲击,2014,33(14):66?71.
ZHANG Zenglei, WU Shijing, ZHAO Wenqiang, et al. Study on dynamic characteristics of high?speed multi?link drive mechanism with clearance [J]. Vibration and impact, 2014, 33(14): 66?71.
[5] 黄海洋,李艳,井超超,等.运动副间隙振动状态实验研究[J].北京印刷学院学报,2010,18(4):16?18.
HUANG Haiyang, LI Yan, JING Chaochao, et al. Experimental study on the vibration state of the clearance of the moving pair [J]. Journal of Beijing Institute of Graphic Communication, 2010, 18(4): 16?18.
[6] 侯雨雷,张占叶,李明洋,等.一种含间隙解耦并联机构动力学分析与混沌现象辨识[J].振动与冲击,2016,35(8):211?218.
HOU Yulei, ZHANG Zhanye, LI Mingyang, et al. Dynamic analysis and chaotic phenomenon identification of parallel mechanism with clearance decoupling [J]. Vibration and impact, 2016, 35(8): 211?218.
[7] 陈予恕.非线性振动、分叉和混沌理论及其应用[J].振动工程学报,1992(3):235?250.
CHEN Yushu. Nonlinear vibration bifurcation and chaos theory and its application [J]. Journal of vibration engineering, 1992(3): 235?250.
[8] 姜俊昭,卢剑伟,张辉,等.考虑间隙运动副耦合作用的车辆摆振动力学行为分析[J].振动与冲击,2016,35(1):66?69.
JIANG Junzhao, LU Jianwei, ZHANG Hui, et al. Dynamic behavior analysis of vehicle pendulum vibration considering coupling of clearance motion [J]. Vibration and impact, 2016, 35(1): 66?69.
[9] LIU C S, ZHANG K, YANG R. The FEM analysis and appro?ximate model for cylindrical joints with clearances [J]. Mechanism & machine theory, 2007, 42(2): 183?197.
[10] GONTHIER Y, MCPHEE J, LANGE C, et al. A regularized contact model with asymmetric damping and dwell?time dependent friction [J]. Multibody system dynamics, 2004, 11(3): 209?233.
[11] KOSHY C S. Characterization of mechanical systems with real joints and flexible links [D]. US: Wichita State University, 2006.

