超声仪表信号的小波去噪及实现
苏映新
摘 要: 提出基于软硬阈值改良折中法的超声仪表信号小波去噪方法,对超声波信号实施希尔波特变换,完成超声波信号的正交相移,提高超声信号的准确度。通过小波阈值去噪中软硬阈值的一种改良折中法对小波实施重构,得到去噪后的超声仪表信号,对软硬阈值折中法的原则实施改进,得到改进的阈值函数,降低软硬阈值折中法操作得到的超声仪表信号的振荡,调整改进阈值函数中的参数,确保参数得到软硬阈值折中内更高的取值范围,增强阈值函数的灵活性,提高超声仪表信号去噪精度。实验结果说明,所提方法可实现超声仪表信号的去噪,去噪性能以及去噪效果良好。
关键词: 超声波信号; 小波去噪; 硬阈值; 软阈值; 改良折中法; 正交相移
中图分类号: TN911.72?34 文献标识码: A 文章编号: 1004?373X(2018)19?0054?04
Abstract: A wavelet denoising method of ultrasonic instrument signal based on the soft and hard thresholds improved eclectic method is proposed, in which the Hilbert transform is used to implement the orthogonal phase shift of ultrasonic signal, and improve the accuracy of ultrasonic signal. A soft and hard thresholds improved eclectic method for wavelet threshold denoising is adopted to reconstruct the wavelet, which can obtain the denoised ultrasonic instrument signal. With the method, the principle of soft and hard thresholds eclectic method is improved to get the improved threshold function, the oscillation of the ultrasonic instrument signal is reduced, which is obtained by the operation of the soft and hard thresholds eclectic method, and the parameters in the improved threshold function are adjusted to ensure the wider value range of the parameter in the soft threshold and hard threshold compromise, enhance the flexibility of the threshold function, and improve the denoising accuracy of ultrasonic instrument signal. The experimental results show that the proposed method can realize the denoising of the ultrasonic instrument signals, and has high denoising performance and perfect denoising effect.
Keywords: ultrasonic signal; wavelet denoising; hard threshold; soft threshold; improved eclectic method; orthogonal phase shift
0 引 言
采用超聲仪表实施超声检测过程中,回波中存在不同类型的干扰波,导致超声波信号受到噪声的干扰,无法获取准确的超声波形,不利于信号的分析以及后续的处理[1]。因此,寻求合理的方法,对检测到的超声信号实施去噪操作具有重要的应用价值。超声波信号是动态时变脉冲信号,信号谱特性沿时间轴延伸,传统方法通过傅里叶变换实现超声信号去噪的过程中,无法解决超声波信号的时变特性,去噪效果不理想。小波分析拥有较强的时频分析局部化属性,可提高超声波信号去噪精度。本文在小波阈值去噪中提出一种软硬阈值改良折中法,实现超声仪表信号的准确去噪。
1 基于软硬阈值改良折中法的超声仪表信号小波去噪方法
1.1 超声回波信号预处理
超声波传感器采集的超声仪表信号拥有局部光滑属性,其正则性取决于[f(t)=h(t)cos t],其中,[h(t)]是超声仪表信号时域函数,超声信号[f(t)]在某时期的Lipschitz指数呈现正无穷变化趋势。如果小波函数[?(t)]包含有限[n]阶消失矩,此时随机时间范围内小波变换模的逐渐衰减同[an]一致([a]是小波系数),该种情况下不能得到超声信号的[n+1]阶导数的局部正则属性,无法获取超声信号和其[n]阶导数局部奇异性小波函数,若受到噪声的干扰,则无法对信号到达的时刻实施准确分析。本文采用希尔波特变换对超声信号实施预处理,再采用小波变换实现超声信号的去噪[2]。
分析式(6)可以得出,[v(t)]的傅里叶变换[V(f)]是信号自身的傅里叶变换[U(f)]同频率的符号函数相乘,再同负虚单位[-j]相乘的结果。分析式(5)可以得出,某个频率的符号函数是在频域对信号频谱实施90°的相移变换得到的。对超声波信号实施希尔波特变换后,完成了信号的正交相移,确保其成为自身的正交对。基于希尔波特变换得到的超声信号正交对能够塑造解析信号,提高超声信号的准确度,为后续超声信号去噪提供可靠的基础[4]。
1.2 小波阈值去噪中软硬阈值的一种改良折中法
以往的硬阈值法基于均方误差能够得到原超声仪表信号的近似最佳预测值,但其光滑性差。软阈值法预测的超声仪表信号同原信号光滑性一致,但是其会导致去噪后超声信号中的相关特征被丢弃。因此,本文提出一种软硬阈值改良折中法,对小波实施重构,得到去噪后的超声仪表信号。该种方法的阈值函数灵敏度高,可实现不同的数学操作[5],有效处理硬阈值函数不连续的弊端,降低软阈值函数的小波系数偏差,增强超声仪表信号的去噪效果。
本文基于小波变换提出超声仪表信号的阈值去噪方法,其核心思维是小波系数[wj,k],噪声引发时,某个临界阈值必然大于小波系数,这时应丢掉[wj,k]。而因超声仪表信号引发小波系数时临界阈值应比[wj,k]小,如果要獲得去噪后的超声仪表信号,那么应该用新的小波系数对小波实施重新构解[6]。采用硬阈值方法和软阈值方法,留存某些[wj,k]或者以零为准收纳某一个固定量。两种方法的示意图如图1所示。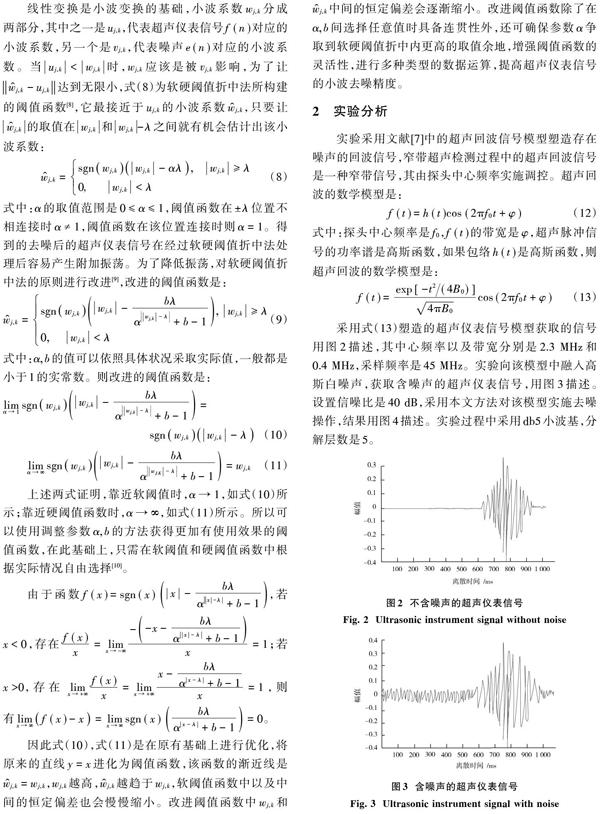
硬阈值法和软阈值法存在一定的误差。从图1得知,为了不让附加振荡作用于去噪后的超声仪表信号,需要小波系数[wj,k]整体连贯性优良,进而使用软阈值法估计得到小波系数[wj,k]。但是重构超声仪表信号和真实超声仪表信号的相近关系又会被[wj,k]和[wj,k]所左右,特别是当出现[wj,k≥λ]时,[wj,k]和[wj,k]将会出现固定的误差。从均方误差方面来说,软阈值法低于硬阈值法。由于[±λ]处的硬阈值法处理函数存在波动[7],导致去噪后的超声仪表信号不连贯,其不具备同原始信号一致的光滑性,使得附加振荡作用在去噪后的超声仪表信号上。均方误差MSE的数学表达式如下:
式(7)证明了假如只在硬阈值法和软阈值法中选取一种,并不能得到十分理想的去噪效果。硬阈值法在超声仪表信号特征的保留上优于软阈值法,但是在信号平滑方面稍差。相反,软阈值法在超声仪表信号平滑方面优于硬阈值法,而在超声仪表信号特征的保留方面却差强人意。
2 实验分析
实验采用文献[7]中的超声回波信号模型塑造存在噪声的回波信号,窄带超声检测过程中的超声回波信号是一种窄带信号,其由探头中心频率实施调控。超声回波的数学模型是:
实验对本文采用信噪比是40 dB的含噪超声波信号模型实施去噪分析,实验采用sym4小波基以及db4小波基,分解层数是5,不同方法的去噪仿真结果用表2描述。
分析表1以及表2 能够得出,本文方法在均方误差以及信噪比上都优于其他两种方法,本文方法在均方误差较低的情况下可提高信噪比,说明本文方法对超声波信号的去噪性能强。分析表1内的quadchirp信号去噪结果可得,受到阈值选择的干扰,软阈值法的超声信号降噪质量降低。分析表2中的结果能够看出,采用sym4的软阈值法和本文方法的去噪性能优于采用db4小波基,而硬阈值法却相反,说明相同方法采用不同的小波基具有不同的去噪性能。
3 结 论
本文提出了基于软硬阈值改良折中法的超声仪表信号小波去噪方法,解决了超声波信号的时变特性,具有较高的去噪性能和去噪效果。
参考文献
[1] 许超.基于改进的小波阈值的电能质量信号去噪[J].电测与仪表,2015,52(5):64?66.
XU Chao. Power quality signal denoising based on improved wavelet threshold [J]. Electrical measurement & instrumentation, 2015, 52(5): 64?66.
[2] 李红延,周云龙,田峰,等.一种新的小波自适应阈值函数振动信号去噪算法[J].仪器仪表学报,2015,36(10):2200?2206.
LI Hongyan, ZHOU Yunlong, TIAN Feng, et al. Wavelet?based vibration signal de?noising algorithm with a new adaptive threshold function [J]. Chinese journal of scientific instrument, 2015, 36(10): 2200?2206.
[3] 陈晓娟,王文婷,李楠.小波熵自适应阈值的电能质量信号去噪新方法[J].电测与仪表,2014,51(15):68?73.
CHEN Xiaojuan, WANG Wenting, LI Nan. A novel denoising method for power quality signal based on wavelet entropy adaptive threshold [J]. Electrical measurement & instrumentation, 2014, 51(15): 68?73.
[4] 蒋薇薇,鲁昌华,张玉钧,等.基于提升小波改进阈值的光谱信号去噪研究[J].电子测量与仪器学报,2014,28(12):1363?1368.
JIANG Weiwei, LU Changhua, ZHANG Yujun, et al. Research on spectrum signal denoising based on improved threshold with lifting wavelet [J]. Journal of electronic measurement and instrumentation, 2014, 28(12): 1363?1368.
[5] 马伦,康建设,赵春宇,等.基于Morlet小波变换的信号去噪及在轴承状态监测中的应用[J].机械科学与技术,2014,33(9):1345?1349.
MA Lun, KANG Jianshe, ZHAO Chunyu, et al. Morlet wavelet transform?based signal de?noising and its application in bearing condition monitoring [J]. Mechanical science and technology for aerospace engineering, 2014, 33(9): 1345?1349.
[6] 申元,马仪,王磊,等.实测过电压/雷电流信号小波去噪方案探究[J].电工电能新技术,2014,33(10):64?69.
SHEN Yuan, MA Yi, WANG Lei, et al. Research on wavelet de?noising scheme for field overvoltage/lightning current signals [J]. Advanced technology of electrical engineering and energy, 2014, 33(10): 64?69.
[7] 杨岳飞,刘辉,谭检平.带噪语音信号小波去噪算法研究[J].计算机工程与应用,2015,51(14):211?213.
YANG Yuefei, LIU Hui, TAN Jianping. Research on wavelet?based speech signal with noise denoising algorithms [J]. Computer engineering and applications, 2015, 51(14): 211?213.
[8] 蔡剑华,李晋.基于频率域小波去噪的大地电磁信号工频干扰处理[J].地质与勘探,2015,51(2):353?359.
CAI Jianhua, LI Jin. Suppression of power line interference on MT signals based on the frequency domain wavelet method [J]. Geology and exploration, 2015, 51(2): 353?359.
[9] 苏成志,陈洪印,孟凡一,等.新阈值二进小波去噪算法在齿轮信号中的应用[J].计算机工程与应用,2014,50(18):206?209.
SU Chengzhi, CHEN Hongyin, MENG Fanyi, et al. Application of new threshold dyadic wavelet de?noising algorithm on gear signal [J]. Computer engineering and applications, 2014, 50(18): 206?209.
[10] 吴秀君.改进提升小波阈值算法在信号去噪中的应用[J].激光杂志,2014,35(8):15?18.
WU Xiujun. Improved wavelet threshold based on lifting wavelet in application of signal de?noising [J]. Laser journal, 2014, 35(8): 15?18.

