基于CAPS, BDS和GPS的组合卫星定位精度分析*

傅圣友，李圣明，王兆瑞

(1. 中国科学院大学天文与空间科学学院，北京 100049；2. 中国科学院国家天文台，北京 100101)

全球导航卫星系统(Global Navigation Satellite System, GNSS)经过几十年的飞速发展，美国的全球定位系统(Global Positioning System, GPS)、俄罗斯的GLONASS、中国的北斗卫星导航系统(BeiDou Navigation Satellite System, BDS)、欧洲的伽利略(Galileo)系统均已建成并投入使用。在亚太区域内，全球定位系统单点定位精度大约为6～10 m，北斗卫星导航系统由于可见卫星数量较多且卫星高度角更高，单点定位精度略优于全球定位系统，大约为4～8 m[1]。

为了能够得到比单系统单点定位更高的定位精度，采用多个导航系统的信号实现联合定位导航是现今导航接收机的一种发展趋势。相比单一导航系统的定位，多系统联合定位可用的卫星数量显著增多，可以通过星座优化选择几何布局更佳、信号强度更好的卫星实现组合定位解算，能有效提高定位的连续性、准确性和稳定性。

中国区域定位系统(Chinese Area Positioning System, CAPS)是中国科学院发明的转发式卫星导航定位系统，是中国二代卫星导航系统的重要组成部分。系统利用现有的C频段通信卫星组建导航星座，并建立了一套与导航相关的地面设施。由地面导航主控站的原子钟提供精确的时间基准，并生成导航电文和测距码，上行至通信卫星。通信卫星上的信号转发器转发导航主控站生成的导航信号，向系统覆盖区域内的用户接收机播发导航信号，使接收机能实时测量、解算，从而获得用户接收终端的位置、速度和时间信息，为卫星定位方法的研究提供了新的思路和实验平台[2]。

本文开展了转发式卫星导航试验系统CAPS与BDS，GPS的组合定位解算，采用分立的BDS/GPS和转发式CAPS导航接收机分别采集各系统的导航电文和码伪距观测量。通过对三系统卫星的优选构成导航星座，并消除系统间钟差，然后进行组合定位解算。最后通过统计，获得了有CAPS信号参与定位情况下的组合定位精度，并与BDS/GPS双系统接收机定位结果进行了分析比较。

1 联合定位方法

BDS，GPS和CAPS三系统联合定位原理如图1，三系统的导航卫星共同组成空间全球导航卫星系统星座。由专用的接收机平台接收三个系统全部可见卫星的导航电文，测量码伪距，并将原始定位数据保存到计算机，最后在计算机中进行离线数据处理，采用最小二乘法进行位置解算，得到联合定位结果，实现三系统联合卫星定位，并对定位精度进行分析。

图1 三系统卫星定位原理图Fig.1 Positioning schematic of three systems

在联合定位解算时，CAPS系统是对传统卫星定位系统GPS和BDS的补充和增强。CAPS系统由于其转发式定位的特色，使用通信卫星实现定位，因此可以为多系统联合定位提供卫星数量、卫星空间布局、灵活性和抗干扰等方面的优势。CAPS系统的加入，可以增加卫星星座的有效卫星数量，优化星座的空间布局，减小位置精度因子值。此外，CAPS系统导航信号采用码速率为10.23 Mcps的测距码，相比于GPS粗码1.023 Mcps和BDS的2.046 Mcps码速率，CAPS更高的码速率可以得到更精确的伪距测量值。而且CAPS的系统时间统一由地面站高精度原子钟提供，没有卫星间的钟差，也能提高定位精度。

1.1 观测方程及线性化

(1)

(2)

代入基本观测方程(1)中，得到：

(3)

其中，卫星位置(Xk,Yk,Zk)及卫星时钟偏差dtk可由卫星星历获得[3-5]。

解算时，对于BDS和CAPS系统，将接收机钟差与系统钟差合并解算，即共有6个未知数Xi,Yi,Zi,dti,(dti-dtB)和(dti-dtC)。当组合系统接收信号的卫星数不小于系统数加3时(即单系统至少4颗卫星，双系统至少5颗卫星，三系统至少6颗卫星)，就可实现组合定位[6]。

(3)式对于接收机位置(Xi,Yi,Zi)是非线性的，所以在使用最小二乘法之前，此方程必须线性化。式中非线性部分如下：

(4)

需要选择一个接收机的初始位置(Xi,0,Yi,0,Zi,0)开始线性化，此处选择初始位置为地心(0, 0, 0)。定义增量ΔX, ΔY, ΔZ如下，用于更新近似的接收机坐标，p为迭代计算次数，每次迭代计算均以前一次计算更新后的位置作为本次计算的初始位置：

(5)

将(4)式在每次迭代计算的初始位置(Xi,p,Yi,p,Zi,p)处泰勒展开，得到：

f(Xi,p+1,Yi,p+1,Zi,p+1)=f(Xi,p,Yi,p,Zi,p)+

(6)

其中，偏导数为

(7)

至此，(3)式变为一阶线性观测方程：

(8)

(9)

1.2 最小二乘法

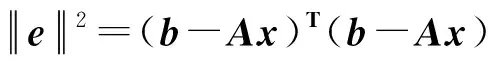
ATAx＾=ATb或x＾=(ATA)-1ATb.

(10)

于是，(8)式可重新写为矢量形式，即

(11)

再将其整理成最小二乘问题Ax=b的常规表达式，即

(12)

(13)

当m+n+l≥6时，有唯一解： ΔXi,p+1,ΔYi,p+1,ΔZi,p+1。此解可以叠加到接收机的初始近似位置上，从而得到下一步更精确的近似位置：

(14)

可以继续用Xi,p+1,Yi,p+1,Zi,p+1代替Xi,p,Yi,p,Zi,p，代入(13)式循环计算，直至q次之后方程的解ΔXi,p+q,ΔYi,p+q,ΔZi,p+q达到期望的误差数量级，q即为最小二乘迭代次数。通常，四到五次循环计算便可符合目标。

2 试验方案及过程

2.1 试验方案

基于BDS，GPS和CAPS的组合卫星定位试验采用静态单点定位方式。试验接收机安装在中国科学院国家天文台楼顶。由于CAPS系统工作在C频段，与其他两系统采用的L频段不同，为了改善信号接收性能，采用分立的接收天线靠近放置。导航射频信号转换到中频后，分别由CAPS接收机和BDS/GPS双系统单频接收机基带捕获跟踪解调，并实时同步记录三系统的卫星星历、伪距等原始定位数据，并存储到计算机。最后在计算机中采用MATLAB软件编程进行数据处理和联合定位解算，并分析试验结果，统计定位精度。定位试验系统框图如图2。

2.2 试验过程

(1) 在天文台楼顶放置一台 BDS/GPS双系统定位接收机，进行48 h连续测量，取其定位解算 结果数值作平均， 获得静态定位参考点坐标值 (x0,y0,z0) 为 (-2 173 764.530 7, 4 383 137.036 6, 4 078 283.873 5)。

(2)在同一位置，分别用BDS/GPS单频接收机和CAPS接收机长期采集定位原始数据，包括全部可见GPS，BDS和CAPS卫星的卫星星历、卫星钟差、电文修正信息、码伪距测量值等。

(3)选取各系统同时段的卫星定位信息，由卫星星历计算每个历元的卫星位置坐标值，同时也采用三系统全部可观测到的卫星用最小二乘法进行定位解算。

(4)处理定位结果数据，分析统计联合定位时定位结果的准确度和精度，与BDS/GPS双系统定位结果作对比，得出试验结论。

2.3 数据统计方法

当设备处于正常工作状态，三系统均成功捕获跟踪信号后，连续记录n(n> 1 000)个历元定位伪距测量数据及期间的导航电文。对n个历元数据进行定位解算，得到每历元的定位解算结果。采用的计算步骤如下：

图2 三系统卫星定位试验原理框图
Fig.2 Schematic of combined positioning experiment

(1)对每个历元，计算各个方向的定位偏差及三维合成总误差：

(15)

其中，xi,yi,zi为第i个历元定位结果的三维坐标，单位为m；x0,y0,z0为静态定位参考点坐标，单位为m。

(2)分别计算各个方向及三维合成总误差的误差平均值和误差标准差：

(16)

(17)

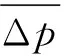
3 试验结果

试验选取2017年9月11日18时19分至9月12日10时34分的测量数据，使用了全部可见的GPS，BDS和CAPS卫星数据，每一时刻能同时接收的卫星最少为16颗，CAPS系统所用卫星详情如表1。

表1 CAPS系统用于本试验的卫星情况表Table 1 Satellites of CAPS used in experiment

采用MATLAB编制CAPS/BDS/CAPS多系统解算程序进行位置解算，解算结果画出平面散点图如图3。双系统、三系统组合时，位置精度因子值情况如图4，定位精度统计结果见表2。

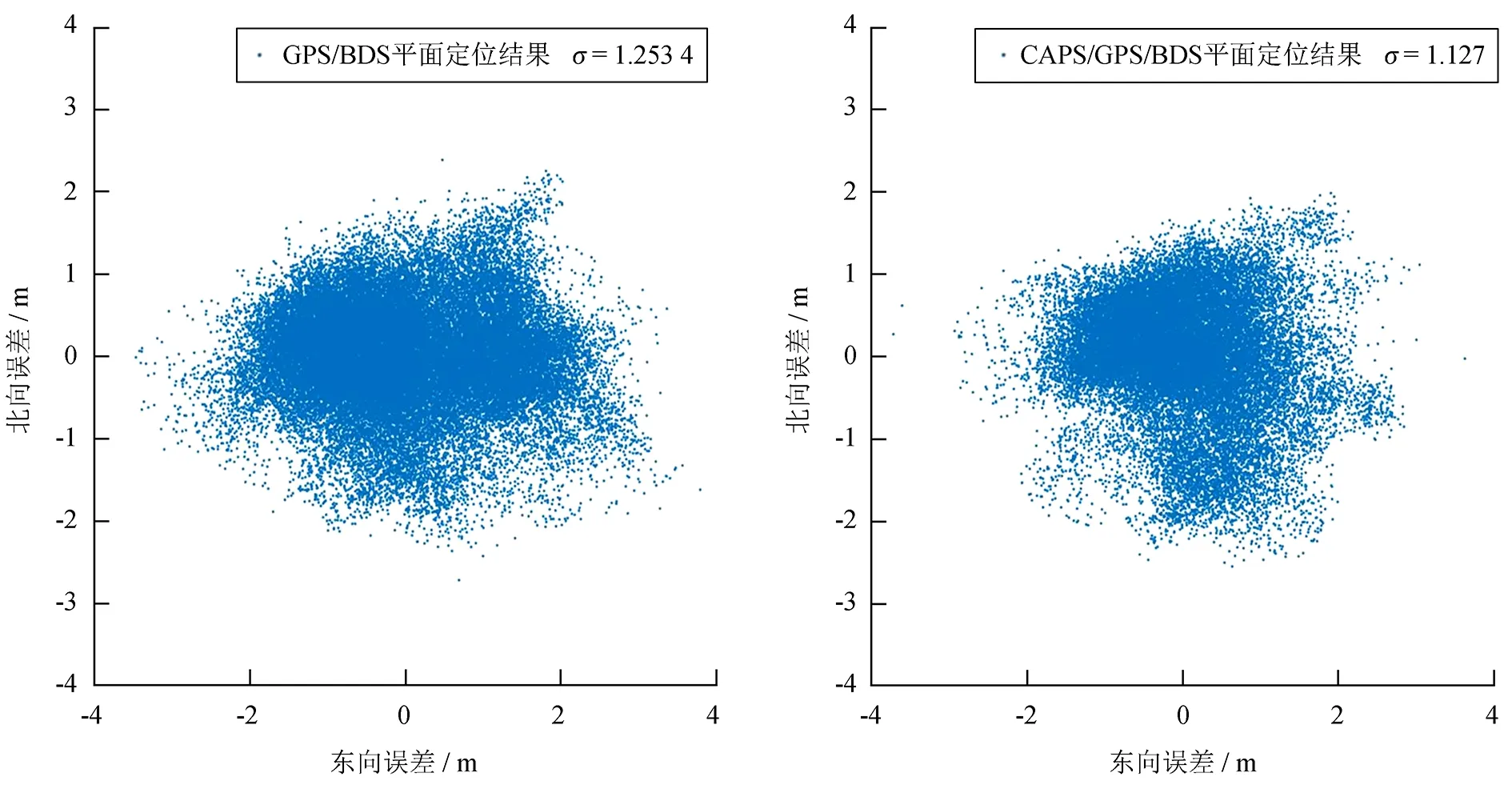
图3 双系统/三系统定位解算误差平面散点图
Fig.3 Positioning horizontal error of GPS/BDS and CAPS/GPS/BDS

图4 双系统/三系统定位解算卫星位置精度因子值变化图
Fig.4 PDOPvalues of GPS/BDS and CAPS/GPS/BDS

4 结 论

由以上结果可以看出，在静态单点定位情况下，CAPS系统的加入，提供了更丰富的卫星选择，改善了空间卫星星座构成，减小了位置精度因子值，因此提高了定位精度，尤其是水平定位精度提高较为明显。在以后的研究中可以通过进一步精细消除误差或采用载波相位测量值参与解算，定位精度还有较大的提高空间。

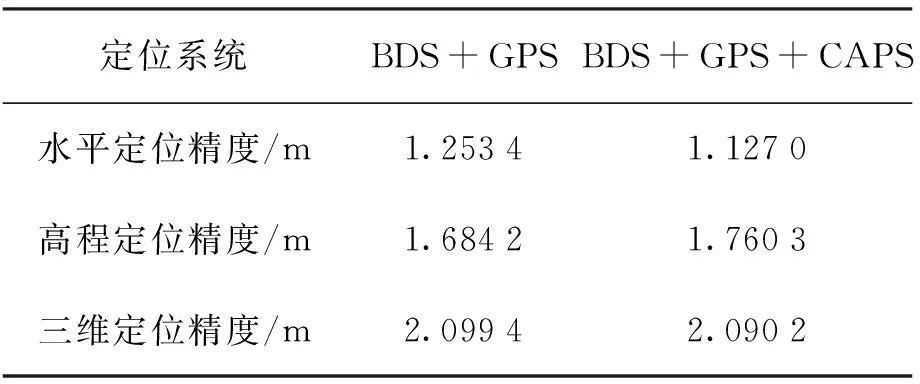
表2 双系统/三系统定位精度统计表Table 2 Positioning accuracy of 2/3 systems