预应力闸墩三维有限元分析及其优化方案研究

韦海勇，王满玉，冯晓波，李馨馨

(1.广西水利电力勘测设计研究院，南宁 530023；2.武汉大学水资源与水电工程科学国家重点实验室，武汉 430072)

随着水利水电工程建设迅速发展、规模逐渐增大，泄水建筑物工作水头不断提高，弧形闸门承受的推力随之增大。巨大的弧门水推力通过支承结构传递到闸墩，在闸墩颈部会出现明显的应力集中现象，产生较大的拉应力，进而导致混凝土发生开裂甚至破坏[1]。为了改善闸墩和支承中的应力状态，近年来，闸墩预应力锚固技术被广泛应用于国内外的水利水电工程中，可有效地减小闸墩拉应力，成为改善大型弧门闸墩结构受力性能的重要措施[2]。

通过改变结构支承形式可提高闸墩颈部的预应力效果。目前的研究工作主要集中在锚块式支承结构及其优化设计。例如，李萌等[2]对预应力闸墩中墩锚块底部接触方式进行了分析，认为锚块底部与闸墩采用分离式接触可大幅度降低拉应力。沈鑫[3]运用有限元法对预应力闸墩进行了三维线弹性计算，同时对2种锚块混凝土强度的预应力闸墩进行分析，认为仅提高锚块混凝土强度对于改善闸墩颈部的受力状态不明显。李树山等[4]利用结构数值仿真模型试验，研究了锚块内设置空腔对预应力闸墩结构受力性能的影响，认为新型空腔式锚块设计方案能够有效地提高闸墩颈部的预压效果。但对于溢流坝中孔泄洪结构，由于孔口宽度较小，大部分情况下闸墩单侧受力，采用深梁形式支承结构可有效改善闸墩偏心受力状态[5]。

目前，针对深梁形式预应力闸墩结构开展的研究较少，尤其对钢结构深梁的研究几乎没有。张竞予等[6]对某水电站泄洪洞采用混凝土深梁结构的预应力闸墩进行有限元分析，认为该结构能够提高闸墩的承载力和刚度。由于深梁形式预应力闸墩整体稳定性较好，因而，有必要进一步开展其在控制闸墩拉应力效果及结构优化设计方面的研究工作。

本文以洋溪水利枢纽溢流坝预应力闸墩为研究对象，针对3种可能的支承结构形式(混凝土深梁式、钢锚块式和钢结构深梁式)下的闸墩进行三维有限元计算。分析了解各方案预应力闸墩结构的应力规律和变形特点，通过综合比较，选定最优的闸墩支承结构方案，并对该方案进行优化分析，确定锚索轴向拉力最优设计值。

1 工程概况

洋溪水利枢纽是广西柳江中下游的防洪控制性工程，该工程以防洪为主，兼顾发电和航运等综合利用。水库正常蓄水位163.0 m，防洪高水位186.8 m，下游水位126.0 m。本工程规模为大(2)型，工程等别为II等，水库总库容为8.5 亿m3。溢流坝共布置10孔，其中8个低孔，其孔口尺寸为7 m×16 m(宽×高)，单个坝段长为16.0 m，墩厚4.5 m，闸室顺水流向长82.0 m。

该溢流坝为碾压混凝土重力坝，泄水坝低孔坝段弧门推力达到70 000 kN。由于弧门水推力巨大，普通拉筋难以满足闸墩的限裂要求，因此采用预应力闸墩。闸墩尾部采用3种可能的支承结构形式，分别为混凝土深梁、钢结构深梁(以下简称钢梁)和钢锚块。闸墩内部和支承结构部位预应力锚索布置分主锚索和次锚索。混凝土深梁和钢锚块主锚索共布设4排，每排7层，辐射角为4°，共计28根；钢结构深梁主锚索共布设4排，每排5层，共计20根。次锚索仅在深梁方案中考虑，垂直于主锚索布置，共布设3列，每列8根，共计24根。图1给出了深梁方案预应力闸墩剖面示意图，其中包括主次锚索布置情况。

2 预应力闸墩三维有限元分析

2.1 模型建立

以溢流坝低孔坝段为研究对象，对单个闸室(包括两侧中墩及其之间的溢流坝)进行建模。预应力闸墩体形复杂，包括混凝土溢流坝、3种闸墩支承结构和预应力锚索。为了尽量减小建模工作量，方便调整和优化结构，本文利用ANSYS软件的二次开发功能，编程实现参数化建模，即针对3种不同支承形式方案建立参数化的三维有限元模型。

采用ANSYS软件建模时，对溢流坝主体部分均采用三维实体单元Solid45，预应力锚索采用三维杆单元Link8，钢梁及钢锚块采用三维壳单元Shell181。为了达到工程所需的计算精度，混凝土结构采用六面体单元进行离散，网格尺寸控制在0.3～0.5 m。计算模型单元总数约26万个，结点总数约29万个。三维有限元网格模型见图2。

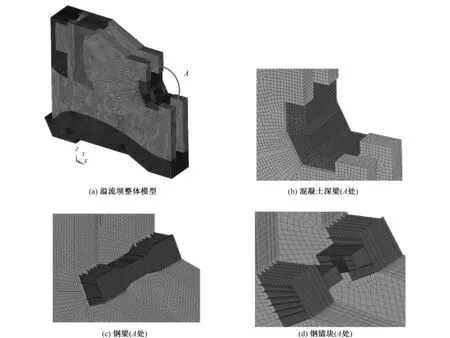
图2 有限元模型Fig.2 Finite element model

2.2 计算方法

有效模拟预应力锚索及钢结构与闸墩间的接触状态是计算中的关键环节[7]。为全面考虑预应力对结构的影响，采用分离法模拟预应力锚索，即分别建立钢筋单元(线单元)、混凝土单元(体单元)和钢梁单元(板单元)。预应力锚索的预拉应力通过设置三维杆单元(Link8)的初应变(实常数之一)来进行模拟。该方法可以准确模拟预应力筋的具体位置和张拉顺序，且能模拟预应力锚索在结构运行过程中的变形情况，从而得到运行过程中的预应力锚索的应力损失[8]。同时，为了较好地模拟钢梁、钢锚块与混凝土闸墩的连接状态，对于钢梁和钢锚块方案，支承钢结构(壳单元)与闸墩混凝土(三维实体单元)的连接采用接触单元。接触状态的表面有如下特点：不互相渗透，能够互相传递法向压力和切向摩擦力，不传递法向拉力。

2.3 基本假定及边界条件

在预应力闸墩的计算分析过程中，混凝土近似假定为均质连续、各向同性的线弹性体，不考虑结构作用时钢筋和混凝土产生的应力重分布。计算边界条件：溢流坝体底面视为固定边界，即在底面各个结点处施加全约束；模型横河向两侧为自由边界。

2.4 材料参数

模型中共涉及3种材料，即混凝土、钢板和预应力锚索。根据混凝土强度等级不同，对模型进行材料分区，各材料力学参数取值见表1。

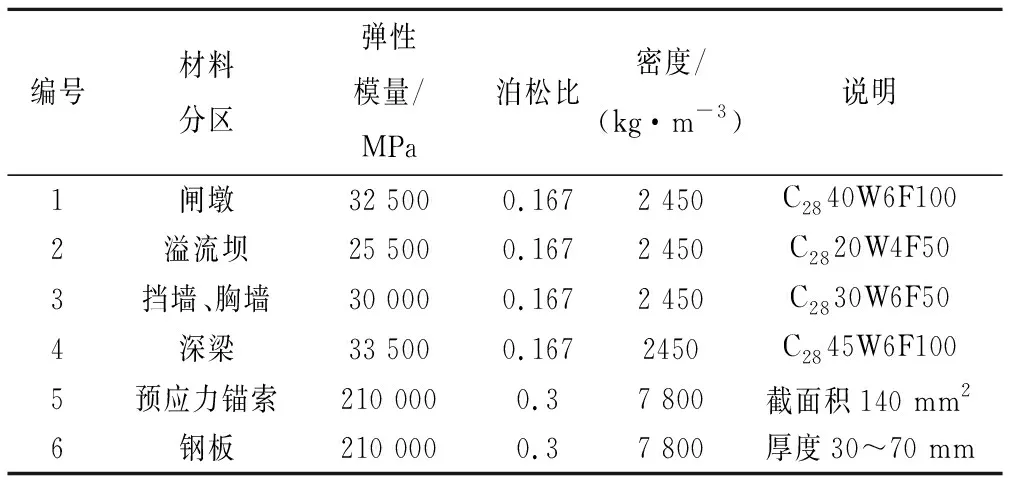
表1 材料力学参数Tab.1 Mechanical parameters of materials

2.5 计算工况及荷载组合

预应力闸墩在运行期，初启门和挡水工况时支铰正压力较大，分别达到36 115和33 710 kN，闸墩及支承结构均会产生较大拉应力。由于初启门为最不利工况，以此工况作为控制工况进行分析。为了对比预应力效果，本研究对混凝土深梁方案计算了无预应力工况。各计算工况与荷载组合见表2。

表2 计算工况与荷载组合Tab.2 Combination of work conditions and loads

3 计算结果及分析

对不同支承结构形式的预应力闸墩进行三维有限元分析，研究各方案溢流坝段各部位的应力～应变特征和支撑体对闸墩应力的影响规律，综合比较选定最优方案，并对预应力锚索预应力进行优化分析。

3.1 闸墩预应力锚索的预应力施加效果

为说明预应力的作用效果，对比研究了预应力施加前后闸墩应力分布规律，并综合分析各方案结构的整体变形特性。以深梁方案为例，对比工况2和工况3的计算结果说明预应力锚索的施加效果。在防洪高水位挡水状态下，施加预应力前后闸墩与深梁接触面的应力分布见图3。

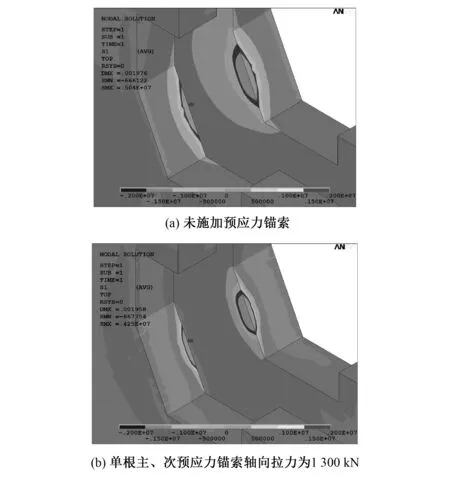
图3 闸墩与深梁接触面第一主应力云图(单位：Pa)Fig.3 The first principal stress cloud diagram of the contact surface between the gate pier and the concrete deep beam

未施加预应力时[见图3(a)]，闸墩与深梁连接处靠上游内侧夹角位置存在较大的主拉应力，最大拉应力达到5 MPa，且范围较大，深度较深，应力超过C40混凝土轴心抗拉强度设计值1.71 MPa，不满足设计要求，将会导致混凝土闸墩和深梁开裂，甚至造成混凝土深梁结构破坏。施加预应力措施后[见图3(b)]，闸墩颈部应力状态得到改善，拉应力范围及大小有所减小，预应力施加对控制闸墩颈部拉应力大小及范围效果明显。

图4给出了初启门工况下，3个方案施加预应力后闸墩的顺河向变形特征。可以看出，闸墩位移指向下游，主要是由上游水压力及预应力锚索共同作用引起，受预应力锚索张拉作用，混凝土产生向预应力锚索张拉方向的位移。其中钢梁方案位移较大，最大值发生在闸墩颈部顶端，大小为0.004 8 m。从拦河坝整体变形上看，溢流坝段底板和预应力闸墩成整体刚度变形，各方案的结构整体性较好，且变形较小，能满足材料强度和结构稳定要求。

图4 闸墩顺水流方向位移云图(单位：m)Fig.4 Displacement cloud diagram in the flow direction of the gate pier

同时，由计算结果可知，主、次预应力锚索在运行过程中因结构变形引起的预应力损失较小，不足预应力的1%(实际拉力值1 300 kN，最大预应力损失10 kN)，其他相似工程也有相同结论[9]。

3.2 支承优化方案比选

针对混凝土深梁、钢结构深梁、钢锚块3种支承形式的预应力闸墩进行细致的应力～应变和破坏机理分析。各方案以预应力锚索拉力抵消1～4倍支座压力分别进行试算。试算时，预应力锚索轴向拉力初始值取为1倍闸门推力，然后预应力锚索的预应力按照每次增加1倍的闸门推力值逐级增加。以初启门工况作为控制工况进行说明。

通过计算，各方案闸墩颈部和支承结构的第1主应力最大值见表3。可以看出，随着预应力的增加，混凝土深梁方案中闸墩颈部产生的主拉应力有所减小，但不明显，反而在深梁底部支座周围产生的主拉应力增加较明显；钢梁和钢锚块方案中闸墩颈部产生的主拉应力增大，且钢结构底面产生的拉应力也有所增加。

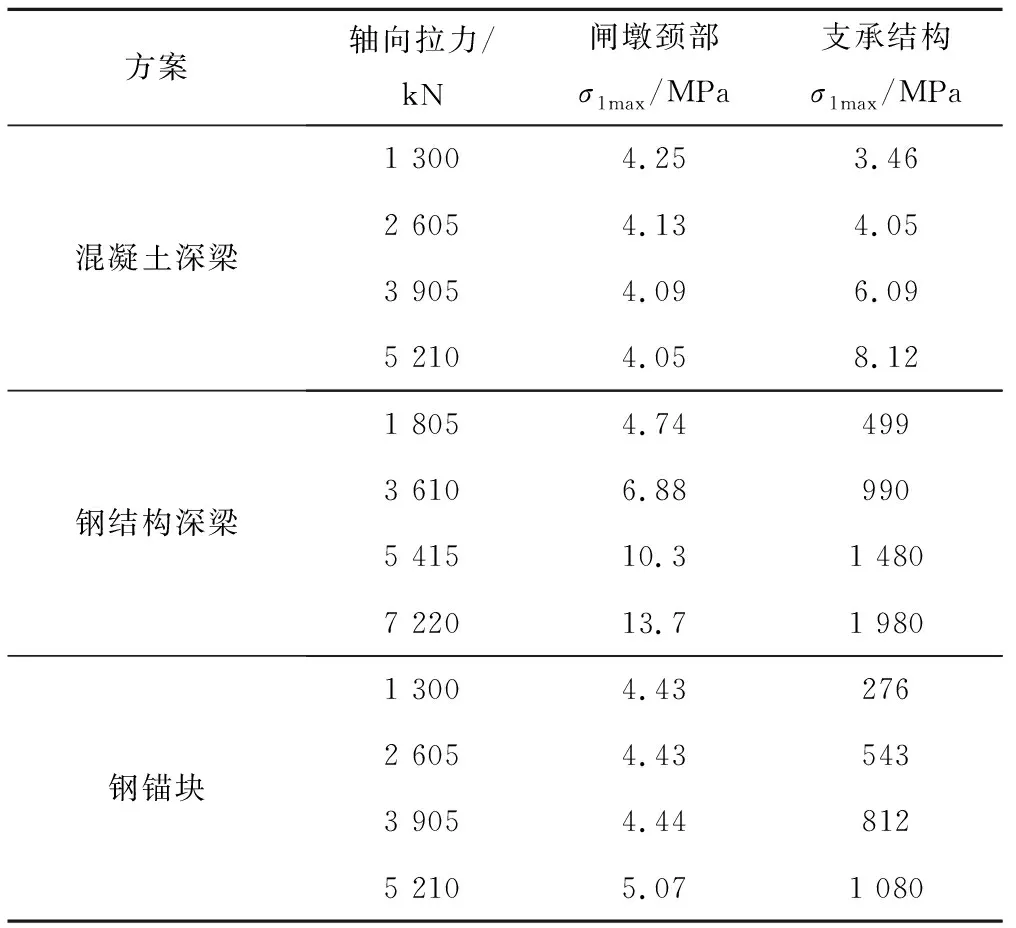
表3 不同轴向拉力值下各部位的最大主拉应力Tab.3 The maximum principal tensile stress in each parts with different axial tension values

为使各方案之间具有可比性，本文最终选取预应力锚索预应力抵消3倍闸门推力进行比较，选定最优的闸墩支承结构方案。

针对混凝土深梁方案，图5给出了闸墩与深梁接触面、深梁底面的第1主应力分布规律。可以看出，预应力的施加会引起闸墩与深梁连接处靠上游外侧夹角位置产生新的拉应力区[见图5(a)]，拉应力最大值为4.09 MPa，且大小随着预应力的增加而减小(见表3)。由于锚束布置对称，闸墩及锚块两侧应力对称分布。当预应力锚索轴向拉力控制在3 905 kN时，闸墩和深梁锚头处局部拉应力均较小，不超过2 MPa。深梁底面支铰轴线部位因承受巨大闸门推力，在与闸墩交界处产生较大的次生拉应力，达到6.09 MPa，但范围较小[见图5(b)]。

图5 混凝土深梁方案第1主应力云图(单位：Pa)Fig.5 The first principal stress cloud diagram of the concrete deep beam scheme(unit:Pa)

图6 钢梁方案第1主应力云图(单位：Pa)Fig.6 The first principal stress cloud diagram of the steel structure deep beam scheme(unit:Pa)

针对钢梁方案，图6给出了闸墩与钢梁接触面、钢梁底面的第1主应力分布规律。可以看出，在混凝土闸墩与钢梁腹板接触处，出现局部压力值较大现象，随着预应力的增加，压力会逐渐增大，同时导致混凝土受压面产生局部拉应力。当主预应力锚索轴向拉力增加到5 415 kN时，混凝土闸墩与钢梁腹板接触处最大压应力为39.5 MPa，主要分布在闸墩两侧。钢梁附近混凝土出现的拉应力区主要在钢梁受压面与上、下面的斜面夹角处，拉应力值达到10.3 MPa，范围向闸墩下游衰减较快[见图6(a)]。同时，主预应力锚索附近的钢梁腹板除承受一定的拉应力之外，由于钢板受力均匀的特点，压应力范围几乎扩展至整个钢梁结构[见图6(b)]。

图7 钢锚块方案第1主应力云图(单位：Pa)Fig.7 The first principal stress cloud diagram of the steel anchor block scheme(unit:Pa)

针对钢锚块方案，图7给出了闸墩与钢锚块接触面、钢锚块底面的第1主应力分布规律。可以看出，承受闸门推力时，因受锚块悬臂的影响，钢锚块与混凝土闸墩之间的压力分布不均匀，闸墩内侧受压小，外侧受压大，这主要由偏心受压产生的弯矩引起。当主预应力锚索轴向拉力增加到3 905 kN时，钢锚块附近混凝土出现的拉应力区主要在钢锚块受压面与下面的斜面夹角处，大小为4.44 MPa，但范围较小[见图7(a)]。随着预应力的增加，该处的拉应力值及范围也逐渐增加。主预应力锚索附近及支铰轴线处的钢梁腹板除承受一定的拉应力之外，压应力范围几乎扩展至整个钢锚块结构[见图7(b)]。

综上所述，从混凝土拉应力控制效果上看，钢梁和钢锚块方案要优于混凝土深梁方案，通过计算发现，不论如何调整混凝土深梁方案横向和纵向的预应力锚索预应力值，深梁处总会存在较大的局部拉应力。对于钢锚块方案，钢锚块在闸门推力作用下存在悬臂作用，这会导致闸墩受压面产生较为明显的不均匀分布压力，局部出现过大压应力，同时也会产生较大的局部次生拉应力。对于钢梁方案，由于钢梁是简支在闸墩上，不存在悬臂作用，闸墩压应力分布较为均匀，因此本文选定钢梁支承为最优方案。

3.3 预应力锚索的预应力设计值确定

目前，预应力锚索设计中拉锚系数的取值主要依靠数值模拟和工程经验，拉锚系数过小则预压效果不明显，过大又将会导致局部拉应力的增大和工程造价的提高[10]。在保证闸墩稳定性和安全性的前提下，为使钢梁方案预应力闸墩处于最佳应力状态，通过设置4组预应力锚索拉力值分别进行试算，分析闸墩的应力状态，得到预应力锚索的预应力设计值。第4排预应力锚索所在位置处的闸墩第1主应力分布规律见图8。

图8 初启门工况下钢梁第4排预应力锚索所在位置处的闸墩第1主应力(单位：Pa)Fig.8 The first principal stress of the gate pier at the location of the fourth row of anchor cables for the steel structure deep beam scheme(unit:Pa)

从图8可以看出，当主预应力锚索轴向拉力为1 805 kN时，闸墩与钢梁接触面压应力较小，不足以保证钢梁与闸墩的连接；当主预应力锚索轴向拉力为5 415 kN时，会导致闸墩与钢梁接触面上、下倒角位置产生较大的拉应力；当主预应力锚索轴向拉力控制在3 610 kN时，闸墩锚头处的局部拉应力较小，为2 MPa左右；当主预应力锚索轴向拉力为7 220 kN时，钢梁与混凝土闸墩之间的压力分布较不均匀，出现局部压力值较大现象。综合不同预应力的计算结果，建议主预应力锚索轴向拉力设计值控制在3 610 kN。

4 结 论

本文采用有限单元法对洋溪水利枢纽工程溢流坝低孔坝段3种支承结构形式的预应力闸墩进行计算，包括混凝土深梁、钢结构深梁和钢锚块，分析了各方案预应力闸墩的应力～应变特性，通过综合比较，选定钢梁方案为最优方案。主要结论如下。

(1) 该水利枢纽溢流坝段的闸墩若按照常规混凝土结构进行设计，在闸墩颈部会产生较大拉应力区，拉应力值高达5 MPa以上，不满足规范要求，因而有必要采用预应力闸墩结构。施加预应力措施可有效减少闸墩颈部的拉应力大小及范围。

(2) 从混凝土拉应力控制效果上看，钢梁和钢锚块方案要优于混凝土深梁方案，考虑到闸门推力下钢锚块的悬臂作用会导致闸墩压力分布不均匀，因此本文选定钢梁方案为最优方案。

(3) 为使钢梁方案预应力闸墩处于最佳应力状态，通过设置4组预应力锚索拉力值分别进行试算，分析闸墩的应力状态，进而得到预应力锚索的预应力轴向拉力设计值。综合不同预应力的计算结果，建议主预应力锚索轴向拉力设计值控制在3 610 kN。

(4) 通过计算发现，主预应力锚索在运行过程中由结构变形引起的预应力损失较小，不足预应力的1%，进一步说明采用分离法可有效模拟预应力锚索预应力的施加效果。

□