中国近20年岩石流变试验与本构模型的研究进展

熊良宵，汪子华

(1.成都理工大学地质灾害防治与地质环境保护国家重点实验室,成都 610059; 2.浙江省工程勘察院，宁波 315000)

1 引言

岩石流变力学的试验和本构模型的研究一直是岩石力学中的研究热点和重点，近20 a国内外已有很多关于这方面的研究报道。国内近10 a随着很多西部深部岩体工程的兴起，包括大型水电工程的引水隧洞、地下厂房等，如锦屏二级水电站的引水隧洞和辅助交通洞。另外，西部很多新的大型铁路隧道和公路隧道即将修建，而其中很大部分隧道也是为深埋隧道，这就为岩石力学的研究带来了机遇和挑战，很多有关岩石力学的科学问题随之出现，而其中岩石流变就是很多深部岩体工程中必须考虑的问题。相对而言，近些年国外的深部岩体工程相对已较少，因此，国内学者在这方面的研究成果已远远多于国外的研究成果。

国内有关岩石流变的研究成果，主要围绕实际工程中所遇到的问题开展了许多试验和本构模型研究，从最初相对简单的单轴和三轴蠕变试验，发展到开展三轴卸荷条件下岩石的蠕变试验、考虑温度影响的轴蠕变试验、考虑含水量的蠕变试验，考虑渗透力的蠕变试验和考虑各向异性影响的蠕变试验等，这主要根据实际工程所需要而开展的研究工作。

有关岩石流变本构模型的研究成果也是比较丰富，包括最初采用广义Kelvin模型、Burgers模型和西原模型对岩石蠕变试验曲线进行分析，发展到提出新的元件流变模型、提出非定常流变模型、损伤流变模型和分数阶流变模型等。

笔者对近年来岩石流变试验和提出非线性流变模型的方法进行了归纳和总结[1]，但近7～8 a来国内又继续有很多有关的岩石流变试验和本构模型的研究成果。因此，鉴于国内外有关这方面的研究现状对比，笔者通过本文将重点归纳和总结国内近20 a来有关岩石流变试验和本构模型的研究成果，而在进行各种类型的研究成果分析和总结时，将只列举各个方向的代表性成果。

2 岩石和结构面的流变试验

2.1 单轴压缩蠕变试验

岩石的单轴压缩蠕变试验是早期开展得比较多的蠕变试验，一般采用分级加载方式，直到试件破坏为止，比较代表性的研究成果有李永盛[2]和徐平等[3]。

曹平等[4-6]则采用分级增量循环加卸载方式对岩石进行了单轴压缩蠕变试验，分级增量循环加卸载方式如图1所示。这种加载方式主要有利于把可恢复的瞬弹性应变、不可恢复的瞬塑性应变、黏弹性应变和黏塑性应变分开进行分析。赵延林等[7-8]采用这种方式对岩石进行了三轴压缩蠕变试验，即围压保持不变，偏应力循环加卸载。

图1 分级增量循环加卸载

另外，也有学者在进行单轴压缩蠕变试验时辅助同时进行其它试验，如刘东燕等[9]采用MTS815液压伺服岩石试验系统和DISP-2声发射监测系统，对重庆市某煤矿深部灰岩进行了单轴蠕变压缩实验，对单轴蠕变实验过程中伴随的声发射特征进行了研究。声发射特征有助于表征蠕变过程中裂纹的产生、扩展和贯通至失稳的发展过程，但目前在蠕变试验过程中辅助进行声发射试验的研究成果相对不多。

2.2 三轴压缩蠕变试验

三轴压缩蠕变试验也是开展得比较多的一种蠕变试验，常规的加载方式便是先施加围压至一定值后，便逐级增加轴压直至试件发生蠕变破坏。代表性的研究成果有赵法锁等[10]、刘建聪等[11]、冒海军等[12]、杨圣奇等[13-14]和范庆忠等[15]。

实际工程中，隧洞洞壁岩体在经历开挖支护时，围岩的主应力会出现先增加后减小，又继续增加的变化过程，而以洞壁岩体的径向应力和切向应力的变化最为明显。因此，实际上需要考虑的是开挖卸荷后岩石的流变特性，2007年开始国内已相继有很多有关岩石三轴卸荷的蠕变试验成果，其代表性的研究成果有朱杰兵等[16-17]、闫子舰等[18]、杨文东等[19]、蒋昱州等[20]、黄达等[21]、张龙云等[22]、邓华锋等[23]和黄兴等[24-25]。

上述是三轴压缩蠕变试验中普遍采用的两种加载路径方式，虽然实际工程中是需要考虑岩石卸荷后的流变特性，但对于实际岩体工程而言，也需要同时考虑从远端开挖至分析断面处时围岩主应力升高的过程。另外，开挖卸荷又支护后，围岩的主应力大小不仅发生变化，围岩主应力的方向也会发生变化，开挖前是最大主应力的方向会变为最小主应力的方向，开挖前是最小主应力的方向会变为最大主应力的方向。因此，在对实际工程进行分析时，需要将这两个过程联合起来，每个阶段采用的本构模型和流变参数也会不一样，而本构模型若采用p和q值来表达，将更符合实际。

另外，有些学者在对盐岩进行蠕变试验时，考虑到盐岩储气库在运营过程中溶腔压力会伴随着注采气过程而发生周期性波动，便对盐岩进行了低频循环荷载作用下的三轴蠕变试验，即为恒轴压、循环围压加载路径[26]。

2.3 双轴压缩蠕变试验

单轴和三轴压缩蠕变试验是开展得比较多的试验，但还有一种压缩蠕变试验，目前也有些研究成果，即为双轴压缩蠕变试验。在有些文章中，由于进行三轴压缩蠕变试验时，采用圆柱体试件，只有围压和轴压，简称为双轴压缩蠕变试验。这种简称与本文、相关研究成果并不相同。在本文中，双轴压缩蠕变试验中试件的受力方式如图2所示。

图2 双轴压缩蠕变试验时试样的受力方式

双轴压缩蠕变试验的受力方式与洞壁开挖后还未支护时这段时间围岩的受力方式相同，因此，模拟的也就是这个阶段围岩的蠕变特性。

国内学者周德培[27]最早开展双轴压缩蠕变试验，随后2000年后国内又有少数学者继续开展了双轴压缩蠕变试验，如刘光廷等[28]、李铀等[29]、熊良宵等[30-33]和朱明礼等[34]。

2.4拉伸和剪切蠕变试验

实际工程中往往是由于拉应力超过岩石的抗拉强度而出现破坏，因此，也有少数学者开展了岩石的拉伸蠕变试验，如孙钧等[35-36]、赵宝云等[37-38]。

由于进行岩石的拉伸蠕变试验时，岩石两端的锚固装置很容易使得岩石会出现偏心受拉，而能够进行拉伸蠕变试验的仪器也不多，故岩石的拉伸蠕变试验成果相对偏少。

同时，有少数学者为了考虑岩石在受剪切状态下的蠕变特性，对岩石开展了剪切蠕变试验，比如刘学增等[39]、徐辉等[40]和王明芳等[41]。在此强调文[39-41]所采用的是完整岩石，与后文介绍的结构面剪切蠕变试验所采用的试件是有所区别的。

2.5 应力松弛试验

在实际岩石工程中，蠕变和应力松弛往往是同时存在的，如当岩体开挖时，变形受到约束时发生应力松弛，部分载荷将转移到附近的领域而引起岩体蠕变，而蠕变的发展又将进一步引起岩体内部的应力松弛[42]。因此，进行岩石的应力松弛试验也同样具有重要意义。国内，已有很多学者开展了岩石应力松弛试验，比如唐礼忠等[43]开展了单轴压缩应力松弛试验，李铀等[44]和熊良宵等[45]开展了双轴压缩应力松弛试验，于怀昌等[46-47]开展了三轴压缩应力松弛试验。

2.6 结构面的剪切蠕变试验

结构面的剪切蠕变试验也是岩石流变力学试验中重要的一部分。在实际中想获取结构面试样比较难，因此，有些学者是采用人工制备的规则结构面试样进行蠕变试验，如沈明荣等[48-51]，有些是因完整岩石中含有夹层，从而视为结构面试样进行蠕变试验，如沈明荣等[52]、张治亮等[53]，还有一种是人为先把完整的岩石试件从1/2高度处劈成2部分，而把中间的面视为结构面，从而进行蠕变试验，比如闫子舰等[54]。

2.7 锚固岩体的蠕变试验

实际地下工程中的围岩通常会采用锚杆加固，而岩体经锚固后的力学性能会有所改变，包括其蠕变特性，因此，也有少数学者针对锚固岩体进行了蠕变试验，如韩立军等[55]和赵同彬等[56]针对锚固岩体进行了压缩蠕变试验，而伍国军等[57]开展了岩石锚固系统界面力学特性的剪切流变试验。

2.8 考虑含水状态和渗透影响的蠕变试验

含水量是影响岩石蠕变特性的重要影响，一般而言，水会影响岩石的瞬时弹性变形、蠕变变形量和稳定蠕变阶段的时间等。国内大部分学者通常是采用干燥试样和饱水试样进行压缩蠕变试验，对比这两种含水情况下岩石的蠕变特性的差异，或者采用自然状态和饱水状态下的两种试样，代表性的研究成果有朱合华等[58]、李铀等[59]、冒海军等[60]、黄小兰等[61]、李江腾等[62]、宋勇军[63]和张春阳等[64]。

文[58-64]所采用两种状态试样进行对比试验，这只能定性的对比分析这两种状态对蠕变特性的影响，但实际地下工程的围岩也并不一定就完全是干燥或者饱水状态，而有可能是介于两者之间的某种状态，这就取决于岩石的含水率。若希望通过进行含水状态的试样的蠕变试样，并依此建立含水率的蠕变模型，就需要采用不同含水率的试样进行蠕变试样，国内有少数学者通过试验研究了含水率对岩石蠕变特性的影响，如龚选平[65]、黄明[66]和李鹏等[67]。

地下工程围岩常处于含水状态，也有很多研究者研究了含水状态对岩石蠕变特性的影响，但实际地下水中往往含有侵蚀性离子，而这些侵蚀性离子对岩石的力学特性包括蠕变特性也会有影响，刘建等[68]针对干燥、饱水以及不同离子浓度和酸碱度水溶液循环流动作用至水-岩反应平衡后的砂岩试件，完成一系列单轴压缩蠕变试验；江宗斌等[69]以大连地铁板岩为对象，开展 NaCl 溶液腐蚀蠕变试验。但有关这方面的研究相对还是偏少。

不仅地下工程的围岩具有流变特性，很多边坡工程的岩体也同样具有流变特性，由于库岸边坡岩体存在饱水-失水循环交替的作用，即干湿交替作用，王新刚[70]针对饱水-失水循环劣化作用下库岸高边坡岩石的流变机理开展了试验研究。

上述都是文献探讨含水状态对岩石蠕变特性的影响，实际上往往需要考虑渗流对岩石的流变力学特性的影响。王如宾等[71]采用先进的岩石全自动流变伺服仪，对坝基坚硬岩石变质火山角砾岩进行渗透水压力作用下的三轴流变力学试验，但只是探讨了蠕变对渗透特性的影响。黄书岭等[72]、沈荣喜等[73]、阎岩等[74]、张玉等[75]和杨红伟等[76]也均开展了渗透水压下的岩石蠕变特性试验，均表明水压可以增强岩石的时效变形能力。但这些试验成果还只是初步的分析渗透水压对蠕变变形的影响，或者是蠕变变形对渗透特性的影响。

2.9 考虑温度影响的岩石蠕变试验

随着地热发电、高放核废料地下贮存、深部地下空间的利用，也逐渐需要研究岩石的力学性质受温度和时间共同作用下的变化规律。因此，国内也有很多学者开展了高温作用下岩石的蠕变特性试验，如刘泉声等[77]、高小平等[78]、刘月妙等[79]、梁玉雷等[80]、茅献彪等[81]、王春萍等[82]和张强勇等[83]；也有少数学者开展了高温后岩石的蠕变特性试验，如武东生等[84]。

2.10 考虑岩石各向异性特性的蠕变试验

各向异性也是影响岩石流变变形的重要因素。实际工程中绝大部分岩石均有各向异性的特性，但很多学者在进行蠕变试验时，为了方便分析，往往视为各向同性岩石，并没有分析层理面与荷载方向间的夹角对蠕变特性的影响。随着近年来大家逐渐对这一问题的重视，国内已有很多研究者开始考虑了各向异性特性对岩石蠕变特性的影响，如王金星[85]、付志亮等[86]、熊良宵等[87]、韩庚友等[88]和吴创周等[89]，但有关这方面的研究还存在很多不足。

2.11 考虑试件尺寸的影响

试件的尺寸大小对岩石的力学特性也会有重要影响，因此，岩石的流变特性也同样存在尺寸效应，国内少数学者对岩石流变特性的尺寸效应进行了试验研究，如夏才初[90]、陈沅江等[91]和熊良宵等[92]。

3 岩石的流变元件模型

流变元件模型是岩石流变模型中的最主要一种模型，也是很多国内外学者重点研究的。流变元件组合模型的基本原理是按照岩石的弹性、塑性和黏滞性质设定一些基本元件，然后根据岩石具体的性质，将其组合成能反映岩石流变属性的本构模型，来模拟实际岩石的应力-应变关系。岩石流变元件模型中比较著名的有Maxwell模型、Kelvin模型、Bingham模型、Burgers模型、理想黏塑性体、西原模型等，但这些传统的线性流变元件模型无论怎么组合均不能反映岩石的加速蠕变阶段[93]，因此，国内有很多学者致力于非线性流变元件模型的研究，建立非线性流变元件模型的途径主要分为以下几种。

3.1 第一种途径

第1种途径是以线性流变元件模型为基础，对其黏塑性体进行修正，用非线性牛顿体来代替黏塑性体中的线性牛顿体，从而提出新的非线性黏塑性体，并与线性黏弹性流变模型组合成新的非线性黏弹塑性流变模型。

邓荣贵等[94]将Bingham体中的线性黏滞体改为非线性黏滞体，非线性黏滞体所受应力与其蠕变加速度大小成正比，将改进后的Bingham体与村山体等模型组合得到可以反映加速蠕变的非线性黏弹塑性流变元件模型，改进后的Bingham体的一维蠕变方程为

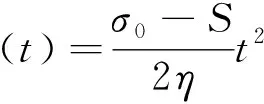
(1)

曹树刚等[95]对西原模型中的Bingham体进行了改进，改进的西原模型能较好地反映岩石的非衰减蠕变特性，改进后Bingham体的蠕变方程为

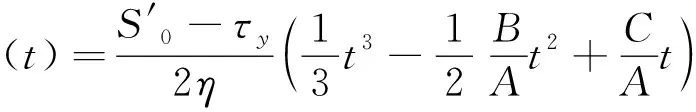
(2)

徐卫亚等[96-97]提出了一个新的非线性黏塑性体，将该非线性黏塑性体与五元件线性黏弹性模型组合得到七元件非线性流变模型，当指数n大于1时，可以反映岩石的加速蠕变特性，其相应的蠕变方程为

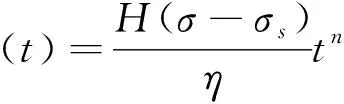
(3)

宋飞等[98]提出2种非线性牛顿体黏滞元件，即SN元件和SP元件，SN元件用来描述岩石的非线性蠕变，SP元件用来描述岩石的加速蠕变，在恒定应力σ=σ0作用下SN和SP元件的蠕变方程分别为式(4)和式(5)，将这两种非线性黏滞元件和线性元件模型组合得到的复合流变模型。

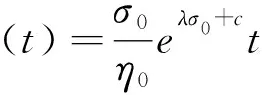
(4)

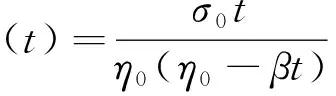
(5)

周家文等[99]定义能够反映衰减蠕变阶段和加速蠕变阶段的非线性函数，并用此函数对广义Bingham模型的蠕变方程进行修正，得到改进Bingham蠕变模型，模型的蠕变方程为

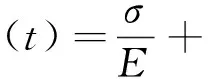
(6)

陈晓斌等[100]提出了非线性黏塑性体(VPB)模型，并与Burgers模型串连形成一个新的非线性黏弹塑性流变模型，非线性黏弹塑性流变模型的流变方程为

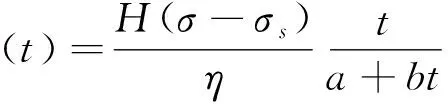
(7)

李亚丽等[101]引入非线性黏塑性元件，将其与 Burgers 模型串联起来，建立一个新的六元件非线性黏弹塑性，非线性黏塑性元件的蠕变方程为

(8)

现将式(1)至式(7)与西原模型中Bingham体的一维蠕变方程(式8)进行对比，可发现其实只是将时间t替换为多项式等时间的非线性函数。

(9)

孙钧[102]以Bingham模型为例研究了η的非线性，认为η应当是所施加的荷载及荷载持续时间的函数。宋德彰[103]认为当采用广义Bingham模型分析围岩的蠕变变形时，Bingham体中的黏滞系数随时间的推移逐渐减小，围岩的黏性变形会随时间的发展而增大，围岩内的黏塑性区也将随时间而加速扩展，即黏滞系数随时间衰减的现象反映了围岩在荷载作用下表现出了加速蠕变特征。此后逐渐有些学者开始考虑对Bingham体或者其它黏塑性体中的黏滞系数进行修正，使其转换为时间和应力的函数。

赵延林等[104]基于幂律型蠕变方程，对Bingham体中的线性黏滞体进行了改进，并将改进的Bingham体和村山体、Hooke体组合得到可以反映岩石加速蠕变的非线性弹黏塑性流变组合模型，其中非线性黏滞体的黏滞系数的表达式为

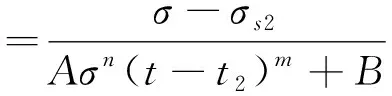
(10)

黄书岭[105]基于Bingham体提出一个考虑应力状态影响的非定常牛顿体，将改进后的Bingham体与Burgers模型组合得到考虑应力状态影响的非定常黏弹塑性流变模型，改进后Bingham体的黏滞系数为

(11)

式中，ηB0为Bingham初始黏滞系数;αηB为Bingham黏滞系数的延迟系数。

蒋昱州等[106]对Bingham体中的黏滞元件进行修正，得到非线性黏滞牛顿体，该牛顿体的黏滞系数与应变有关，并将改进后的Bingham体与Burgers模型组合得到非线性黏弹塑性蠕变模型，该非线性黏滞牛顿体的本构关系为

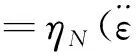
(12)

罗润林等[107]对Bingham体中的黏滞元件进行改进，将改进后的Bingham体与非定常Kelvin体组合得到非定常参数西原模型，其中Bingham体黏滞系数的表达式为

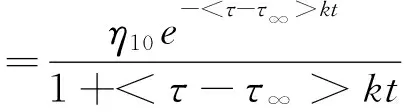
(13)

3.2 第二种途径

第2种途径是以Burgers等线性流变模型为基础，根据Mohr-Coulomb等屈服准则提出一个新的塑性元件，将塑性元件与线性流变模型组成新的非线性黏弹塑性模型，如FLAC3D中比较著名的Cvisc模型，就是将Burgers模型与M-C塑性体串连组建而成的非线性流变模型[108]，Cvisc模型如图3所示。

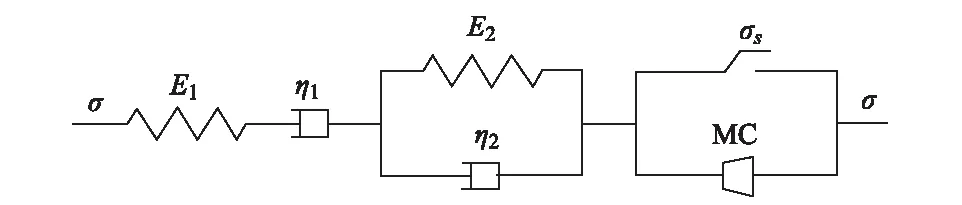
图3 Cvisc流变模型

Cvisc模型比Burgers模型多了3个参数，即M-C体的黏聚力c、内摩擦角φ及抗拉强度σt，Burgers体的参数由拟合蠕变试验曲线得到，M-C体参数由材料常规试验确定。

Guan等[109]又对这一模型进行了改进，考虑了MC体中黏聚力c，内摩擦角φ和膨胀角ψ的弱化效应，其中c和φ的弱化规律为

ωcR(R≥Rthr,c≥cres)

(14)

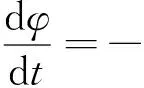
(15)

(16)

Cvsic模型和文[109]所提出的模型均主要适合于软弱岩石，因此陈炳瑞等[110]将Burgers模型与CWFS模型[111]组合成适合于硬脆岩的黏弹脆塑性组合模型。

采用Cvisc模型、改进的Cvisc模型或者Burgers-CWFS模型进行计算时，只要参数取得适当，计算得到的应变与时间关系曲线能出现加速蠕变阶段，但是这类模型没有明显表征加速蠕变的参数，而且强度参数或者强度衰减系数也很难确定，这也是在应用这类模型时存在的问题。

3.3 第三种途径

第3种途径是将线性流变模型中的黏弹性模量或者黏滞系数转换为时间的非定常函数，即建立非定常流变模型。吕爱钟等[112-113]最早在页岩蠕变试验数据的基础上，分析岩石黏弹性变形随应力水平和时间的变化规律，通过反分析方法建立一维情况下非定常黏弹性模型的蠕变方程，该模型主要是将H-K体的黏弹性模量EK转换为时间的函数，非定常H-K模型的一维蠕变方程为

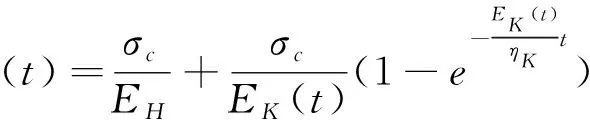
(17)

后续有很多研究者在此基础上又建立了新的非定常黏弹性模型，如罗润林等[114]将Burgers模型中的Maxwell黏滞系数看成为时间的非定常函数；秦玉春[115]将Burgers模型中的黏弹性模量转换为时间的非定常函数；朱明礼等[116]将Maxwell蠕变方程中的剪切模量和黏滞系数变为时间的函数，得到非定常Maxwell模型。

3.4 第四种途径

第4种途径是将线性流变元件模型与损伤力学、断裂力学模型耦合得到非线性流变元件模型。郑永来等[117]基于Weibull分布函数得到损伤参量，对广义Kelvin模型进行修正得到连续黏弹性流变模型；王乐华等[118]则基于Weibull函数建立一个损伤元件，并将其和弹性元件、塑性元件和黏性元件串并连建立一种岩体弹塑黏性损伤力学模型；徐卫亚等[119]建立了可以反映绿片岩加速蠕变的损伤蠕变模型；范庆忠等[120-121]以Burgers模型为基础，引入非线性损伤、硬化变量代替Burgers模型中的线性损伤、硬化变量，从而提出了可以描述软岩蠕变过程三阶段的非线性蠕变本构模型；陈卫忠等[122]以Burgers模型为基础，使Maxwell和Kelvin体的黏弹性模量和黏滞系数变为黏性应变的函数，建立盐岩的蠕变损伤演化方程，并依此建立盐岩非线性蠕变损伤本构模型；朱昌星等[123]以徐卫亚等[97]所提的非线性黏弹塑性流变模型为基础，根据时效损伤和损伤加速门槛值的特点，建立非线性蠕变损伤模型。

3.5 第五种途径

第5种途径是提出一个新的元件，并与现有的线性流变模型组合得到非线性流变元件模型。余启华[124]提出将西原模型中的塑性元件用一个扩裂元件来代替，扩裂元件在加速蠕变之前与塑性元件的作用相同，在进入加速蠕变之后则反映加速蠕变特性，从而形成可描述流变全过程的模型；韦立德等[125]根据岩石黏聚力在流变中的作用提出了一个新的SO非线性元件模型，建立了新的一维黏弹塑性本构模型；陈沅江等[126-127]提出了蠕变体和裂隙塑性体两种非线性元件，并将它们和描述衰减蠕变特性的开尔文体及描述瞬时弹性变形的虎克体相结合，建立了一种可描述软岩的新复合流变力学模型；杨圣奇等[128]基于Weibull分布函数提出一个新的非线性流变元件(NRC模型)，并将NRC模型与西原模型相串连，建立了一个新的岩石非线性流变模型；齐亚静等[129]通过在西原模型上串联一个带应变触发的非线性黏壶，提出改进的西原模型；张治亮等[130]利用改进的非线性流变元件，建立了四元件非线性黏弹塑性流变模型。

3.6 第六种途径

第6种途径是基于分数阶微分理论，采用分数阶非线性黏壶元件替换常见元件模型中的线性黏性元件，从而建立非线性流变本构模型。如殷德顺等[131]利用Riemann-Liouville的分数阶微积分算子及理论，建立了一种新的岩土流变模型元件；孙海忠等[132]利用含分数阶导数的黏壶取代开尔文模型中的线性黏壶，构建了分数导数开尔文模型；康永刚等[133]用分数单元代替伯格斯模型中并联的黏壶，给出分数伯格斯模型；陈 亮等[134]根据Riemann- Liouville 分数阶微积分理论，借鉴经典元件组合的建模思路，提出了统一采用基于分数阶微积分形式表达的四元件非线性黏弹塑性流变模型；吴斐等[135]在非牛顿流体黏滞阻尼元件的基础上提出了分数阶非线性黏壶元件，并通过引入该元件建立了新的非线性蠕变本构模型；周宏伟等[136-137]构建了变黏性系数Abel黏壶本构关系，基于分数阶微分理论，采用将变黏性系数Abel黏壶替代西原正夫模型中牛顿黏壶的方法，建立了盐岩蠕变损伤本构模型；何志磊等[138]用 Abel黏壶替换西原模型中的牛顿黏壶，推导出基于分数阶导数的蠕变本构方程。

4 结论

(1) 有关岩石流变试验的研究成果已比较多，包括单轴、双轴和三轴压缩流变试验，在流变试验中也考虑了很多因素，包括含水量、岩石各向异性、渗透、温度、锚固和试件尺寸的影响，但有关这方面的研究成果相对还比较少，还有待于进一步研究。

(2) 岩石的流变元件模型已发展很多种模型，有很多种途径建立非线性流变元件模型，但有些模型的建立存在缺点，包括缺乏建立的依据，以及有些模型本身含有错误。