晶振电路探究性实验设计

陈世海, 王 军, 代 伟, 王艳芬, 毛会琼, 李 明

(中国矿业大学 信息与控制工程学院, 江苏 徐州 221116)

晶振电路是指采用石英晶体谐振器(简称晶振)作为选频元件的振荡电路,因其频率精准且稳定度高,常被选作标准频率或脉冲信号源[1-4],广泛应用于通信、计量、工控、嵌入式系统、广播电视等领域,特别是在嵌入式系统中,几乎所有的微处理器、CPLD/FPGA、以及DSP等数字集成芯片都采用晶振电路为系统提供时钟脉冲。

晶振电路也是通信电子电路、高频电子线路等课程实验教学中的一项重要内容。现有实验基本属于基础的验证性实验[5-12],侧重于加强学生对振荡电路工作原理的理解,对确保理论课教学效果起到了重要的支撑作用。然而从高等工程教育培养目标的视角来看,实验教学应该尽量面向工程实践,致力于培养学生“解决复杂工程问题”的能力。如果能够有针对性地在现有实验基础上,融入实际工程问题,拓展基础实验的探究性内涵,不仅可以充分利用现有实验资源,还能有效提升实验的工程教育质量。

本文在现有晶振实验的基础上,以广泛使用的Pierce振荡器为切入点,本着《工程教育认证标准》[13]及其OBE(outcome based education)教学理念,将嵌入式系统设计等工程实践中常见的晶振选型及负载电容对振荡性能的影响等问题,作为探究性内容引入实验教学,将“工程知识”“问题分析”和“研究”等3个方面的毕业要求,蕴含于整个实验教学过程,着力培养学生“解决复杂工程问题” 的能力。

1 实验原理

1.1 晶振电特性

石英晶体具有正反压电效应,将其按照一定方向切割成石英晶片,两边敷上银电极并焊上引脚,用金属或者玻璃封装后即构成了晶振[3-4]。通常,为得到晶振等效电路,可将石英晶片机械系统类比于电系统,即石英晶片的质量类比于电感,弹性类比于电容,机械摩擦类比于电阻[6]。晶振等效电路如图1所示,其中石英晶片被表示成串联RLC回路,Lm代表动态电感,其数值决定于晶片厚度；Cm为动态电容,决定于晶片尺寸及电极面积；Rm为动态电阻,取决于机械损耗。此外,对于石英晶片两面敷银层电极、支架和引脚间存在的电容,统一表示为静电容Co。

图1 晶振等效电路

通过图1所示等效电路,可以得到在振荡频率为fr时晶振管脚之间的阻抗：

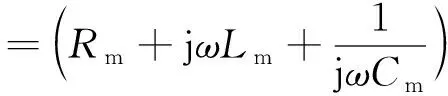
(1)

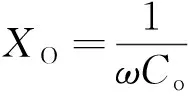
为便于分析,将式(1)中晶振复阻抗的实部Re和虚部Xe分别表示为

(2)

(3)

1.2 Pierce振荡器

Pierce振荡器是Colpitts电容三点式振荡器的变形,它可以工作在几kHz到几百MHz的频率范围,因其结构简单、成本低廉,而且精度高、波形好,特别是功耗低以及对电源电压和环境温度等因素不敏感,所以在工程实践中应用非常广泛,尤其是在数字集成电路中,绝大多数芯片的时钟电路都采用了Pierce振荡器[14-15]。该振荡器电路原理如图2(a)所示,其主要由反相器Inv、反馈电阻RF、晶振JT和电容C1、C2构成。反馈电阻的作用是通过引入反馈使反相器的功能等同于放大器,反馈电阻使放大器在输出电压等于输入电压时产生偏置,迫使反相器工作在线性区域,反馈电阻与反相器通常集成于芯片内部。外接的晶振和2个电容构成选频回路。图2(b)所示交流等效电路中,将反相放大器等效为受控电流源,控制电压为反馈电压VI,跨导为gm；晶振采用式(1)—式(3)给出的阻抗形式。

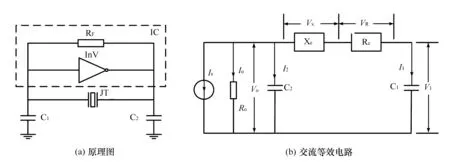
图2 Pierce振荡器

为方便后面分析负载电容对振荡频率及起振的影响,首先采用闭环相位分析法[16]确定Pierce振荡器工作时的电压、电流及阻抗关系,再结合电路工作原理给出负载电容的定义。设图2所示的Pierce振荡器处于稳定振荡状态,其振荡频率为fr。由反相器性质可知,此时反相器输出电流IS滞后其输入电压VI的相角为180°,然后由欧姆定律可得图2(b)交流等效电路中相应电压、电流和阻抗之间的幅值与相位关系为

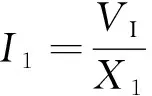
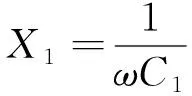
电压、阻抗及电流相位关系如图3所示。

图3 电压、阻抗及电流相位关系

由图3(a)中电压矢量关系可得反相器输出电压VO为

(4)

再由图3(b)得到

1.3 负载电容对振荡频率的影响

在实际应用中,如果所采用的晶振负载电容参数选择不当,不仅无法得到晶振的标称频率,而且还可能导致工作不稳定,甚至导致电路无法正常起振。负载电容不是晶振自身参数,而是振荡电路的参数。设从图2晶振JT两端看进去除晶振外的电抗为XCL,根据巴克豪森准则(Barkhausen Stability Criterion)：电路若能稳定振荡,振荡回路总电抗为0时,才能满足相位平衡条件[2],于是可得

Xe=XCL

(5)

由于在Pierce振荡器中,晶振等效成电感,所以XCL必然为容抗,其对应的电容即为负载电容,记作CL,于是由式(5)可得

(6)

可见,Xe与负载电容CL之间存在等量关系,同时依据1.1节的分析,Xe又是振荡频率fr的函数,所以可以看出振荡频率与负载电容应该存在一定的关系。

根据图3(c)所示电流相位关系,并由基尔霍夫电流定律,可得

I1=I2cosθ-IOsinθ=

再代入式(4)可得

化简并整理得：

(7)

由式(5)、式(6)和式(7)可得

(8)

由式(8)可见,负载电容CL不仅受电路中C1、C2的影响,还受晶振工作时等效阻抗的实部Re和反相器输出的电阻RO影响。通常Re数值远小于RO数值,从而,式(8)可以近似表示为

(9)

需要说明的是,图2(a)并没有考虑分布电容的影响,在精度要求高时,可以将晶振两管脚之间的分布电容并入Co,两管脚对地的分布电容分别并入C1、C2即可。

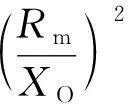
所以可将式(3)进一步简化为

(10)

由式(6)和式(10)可得

(11)

同时,由于在电路振荡时有ω≈ωs,故有

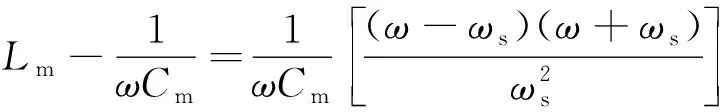
(12)

由式(11)和式(12)可得

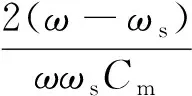
整理后电路振荡频率fr为

(13)

由式(13)可知,电路振荡频率fr不仅取决于晶振自身参数,还取决于负载电容CL。尽管CL不是晶振的一部分,但晶振的标称频率是厂家在晶振手册中指定的负载电容下得到的[17]。因此,若使振荡器工作在晶振标称频率上,则必须使负载电容CL达到晶振手册中指定的数值。

1.4 起振的影响因素

Pierce振荡器结构简单，性能优异,其主要缺点就是所用放大器必须具有足够高的增益,才能补偿选频回路产生的损耗。而振荡器能否稳定振荡,主要取决于能量损耗的大小及放大电路的补偿能力。在振荡时,晶振损耗由晶振等效阻抗的实部Re决定,Re代表了晶振串入到振荡电路中的等效电阻,也被称为等效串联电阻,记作ESR( equivalent series resistance) 。ESR数值越大则晶振在振荡时的损耗就越大,就越容易导致振荡不稳定甚至停振,反之ESR越小则振荡器越容易起振。由式(2)、(11)可得,振荡时有

又

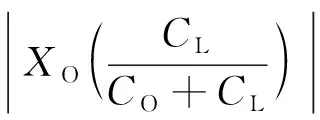
所以可得

(14)

晶振ESR的具体数值一般由生产厂家给出,每个振荡器所允许的ESR值都有一个极限最大值,如果超过这个值将导致振荡不稳定和停振[18-19]。

晶振电路是否容易起振,不仅取决于晶振ESR数值,还取决于反相放大器的跨导。由图3(c)并根据基尔霍夫电流定律可得x轴方向上的电流关系

IS=IOcosθ+I2sinθ

(15)

再由图2(b)、欧姆定律及式(14),可将式(15)表示为

整理后可得

(16)

在微处理器等数字集成电路中,通常选择C1=C2,同时又有Re≪RO,所以可以将式(16)化简后得到

gm=4×ESR×(2πf)2×(CO+CL)2

(17)

根据巴克豪森准则,振荡器在稳定振荡时,放大器增益处于维持振荡的最小值,所以式(17)给出的gm即为Pierce振荡器维持稳定振荡所需的最小跨导gmc。根据Vittoz的理论,振荡电路中反向放大器跨导gm必须满足gm>gmc才满足起振的振荡条件,通常为保证可靠的起振,应满足(gm/gmc)>5[19]。在实际应用中gm/gmc被称为增益裕量。

晶振选型时,主要依据生产厂家给出的晶振标称频率f、CL、Co和ESR。首先要使负载电容CL达到厂家规定的数值,这样才能获得晶振的标称频率；其次依据式(17)计算晶振所要求的反相放大器最小跨导,最后据实际电路的反相放大器跨导(一般由其所在集成芯片的数据手册给出)计算增益裕量,如果发现增益裕量低于5,则说明所选晶振不利于起振,应该选择ESR更小或者CL更小的晶振,然后再重新判断是否满足起振要求。

2 实验设计

实验设计遵照工程教育专业认证中的OBE教学理念,以学生为中心,将实际工程中的Pierce振荡器设计融入实验,主要从工程教育专业认证提出的“工程知识”“问题分析”和“探究”等3个方面的毕业要求入手,着力培养学生解决复杂工程问题的能力。

2.1 课前预习

该阶段主要目标是培养学生自主学习并掌握相关“工程知识”的能力,具体任务为：

(1) 深入学习Pierce振荡器工作原理,依据巴克豪森准则或负阻原理分析振荡器工作过程,并分组讨论负载电容对振荡器的影响；

(2) 从STATEK、EPSON等主流晶振生产厂家网站下载晶振数据手册,了解晶振主要参数及特性；到ST(意法半导体)公司网站下载STM32F103微处理器数据手册,了解该处理器晶振电路参数,并说明如何据此选择满足要求的晶振；

(3) 应用74HC04U设计一个8 MHz的Pierce振荡器,并给出测试负载电容对振荡器性能影响的方法与实验步骤；

(4) 分析负载电容分别为6 pF和12 pF的32.768 kHz晶振对STM32F103处理器LSE时钟性能的影响,并设计测试步骤。

2.2 课上实验

课上实验侧重于培养学生面向工程实际的“问题分析”能力,主要包含以下两方面内容：

(1) 应用74HC04U等器件,在通信电子电路综合实验箱上搭建一个8MHz的Pierce振荡器,调节反馈电阻和负载电容,分别测试示波器探头在×1和×10情况下的输出波形和振荡频率,并详细记录波形与频率变化情况；

(2) 分别测量STM32F103处理器LSE时钟在32.768 kHz晶振负载电容为6 pF和12 pF的起振时间和振荡频率,测试次数不少于10次,每次测试间隔5 s以上时间,详细记录每次测量数据及出现的实验现象,特别是“偶发的”或“反常的”实验现象。

2.3 课后探究

实验前所掌握的工程及理论知识往往不能充分地解释或阐明实验现象和实验问题,需要学生在课后针对实验中出现的问题、现象,深入探究实验表象后面的工程技术知识和理论问题,并在此基础上形成具有实践意义的指导性原则或方法。该阶段具体任务主要包含以下5个方面：

(1) 分析负载电容对振荡频率、起振时间和振荡器稳定度的影响；

(2) 结合实验数据,分析示波器探头×1和×10的区别及其对测试电路的影响；

(3) 分析STM32F103处理器LSE时钟振荡偏差的产生原因,以及在所选晶振负载电容为12 pF时振荡不稳定的原因,分析振荡器临界跨导、负载电容和串联等效电阻对振荡性能的影响；

(4) 总结Pierce振荡器及数字集成芯片时钟电路设计方法和晶振选型时的注意事项；

(5) 撰写实验报告。

3 总结

晶振电路在通信、电子等相关工程实践中应用非常广泛。本实验在原有晶振电路验证性实验的基础上,将数字集成电路Pierce振荡器设计中普遍存在的晶振选型、电路振荡频率、起振以及电路测试等工程问题,有机地融入到整个实验过程,面向《工程教育认证标准》中提出的“工程知识”“问题分析”和“探究”等3个方面的毕业要求,着力于培养学生解决“复杂工程问题”的能力。通过在实验中融入实际工程问题,不仅增强了原有验证性实验的深度和广度,更在实验中强化了对学生工程实践能力的培养,同时也对其他验证性实验的教学改革具有一定的借鉴意义。