二维阵列换能器声辐射力分布的计算分析

徐佳新，马建敏



二维阵列换能器声辐射力分布的计算分析

徐佳新，马建敏

(复旦大学航空航天系，上海 200433)

利用角谱理论得到了圆形活塞换能器阵元组阵后作用在平面悬浮物体上的声辐射力分布公式。通过数值仿真，分析了换能器频率、阵元间距以及阵元数目对声辐射力分布的影响。计算结果表明，换能器组阵使得声辐射力分布的指向性变窄，强度增强；随着换能器频率的提高、阵元间距的增大以及阵元数目的增多，声辐射力分布的主瓣更尖锐，但阵元间距的增大会使声辐射力分布的旁瓣增高。为了改善声辐射力的空间分布，采用伪逆矩阵算法，以能量增益为目标函数，通过调节换能器阵元表面振动速度的幅值和相位来形成多焦点的声辐射力分布，为阵列换能器声辐射力分布的调控和声悬浮稳定性的研究提供帮助。

阵列换能器；角谱理论；声辐射力分布；空间调控；

0 引言

声悬浮较于磁悬浮，最大的优点就是不受悬浮物材料限制，因此具有广阔的应用前景。国内外学者在声悬浮方面也颇有研究。文献[1]中通过驻波悬浮实现了无容器条件下Ni-Sn合金的共晶生长。驻波比行波能产生更大的声辐射力，让物体稳定在波节点处，但要求悬浮物体要远小于半波长。对于大物体，可以采用近场悬浮，Su Zhao等[2]激励直径为120 mm的铝圆盘，成功地将16 g的光碟悬浮了半波长高度。

为了获得更强的声辐射力，可采用换能器组阵的方式，经过实验发现换能器组阵的确可以把物体悬浮到更高位置，远远不只是近场悬浮所说的半个波长高度；不过换能器组阵以后会使得声场的指向性增强，并且悬浮物体受到的声辐射力分布也变得很复杂。为了提高声悬浮的稳定性，可以调节二维换能器阵元表面振动速度的幅值和相位来调控声场，使得声辐射力分布趋于平均。本文以圆形活塞换能器为例，采用角谱理论推导出换能器组阵后作用在远场平面悬浮物体上声辐射力的分布公式，分析换能器频率、阵元数目、阵元间距对声辐射力分布的影响，并且采用伪逆矩阵算法，以能量增益为目标函数，通过调节换能器阵元的表面振动速度的幅值和相位来形成多焦点的声辐射力分布。

1 换能器组阵声辐射力分布计算

对于任意声场可以看成一系列不同振幅的平面声波的叠加[3]：

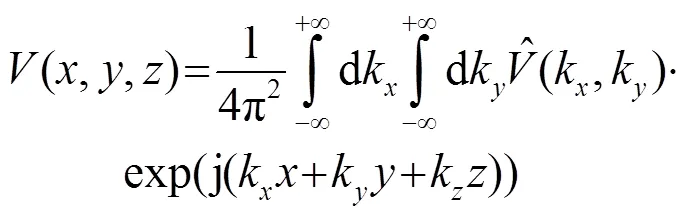
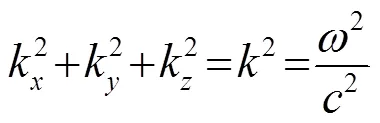
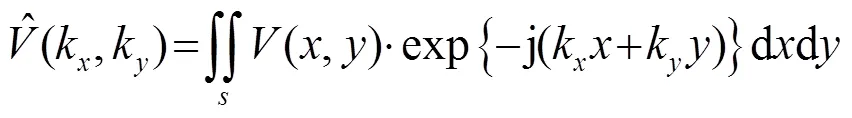
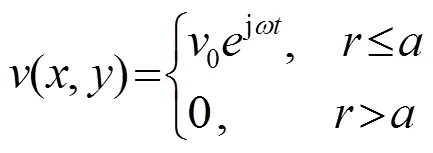
那么，该阵元的振动速度角谱由傅里叶-贝塞尔变换可得[4]：

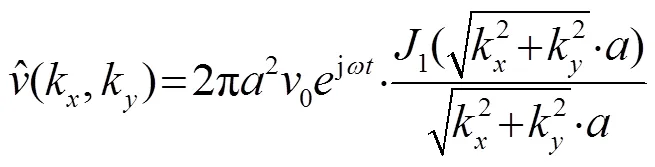
按照图1排布的换能器阵的振动速度角谱可以采用阵列原理来计算。

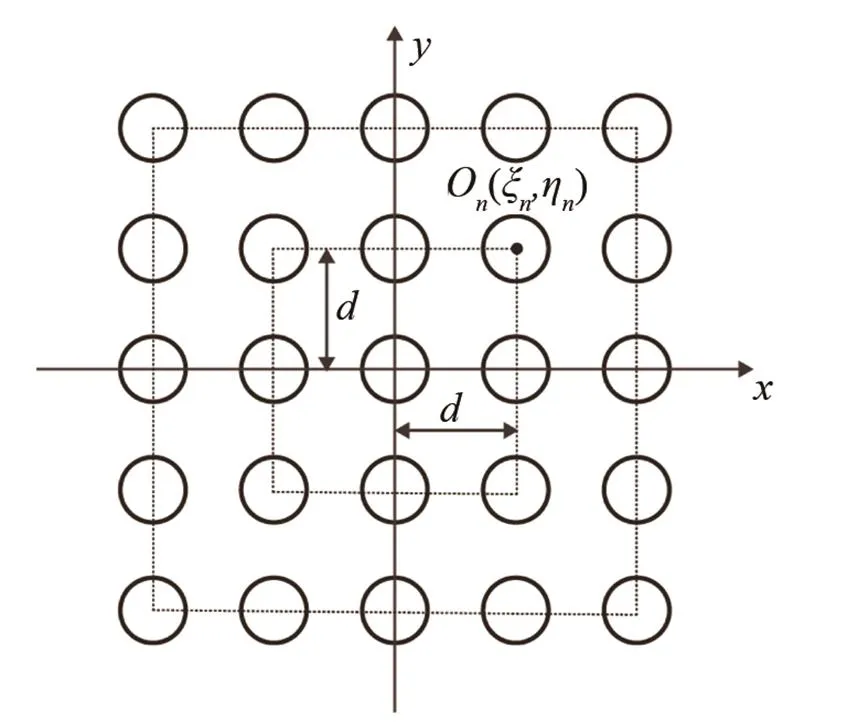
图 1 二维换能器阵列

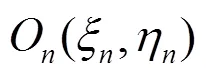
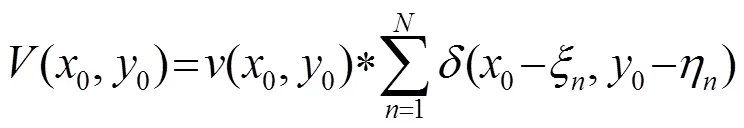
将式(6)代入式(3)，再由卷积定理，求出换能器阵表面振动速度角谱为

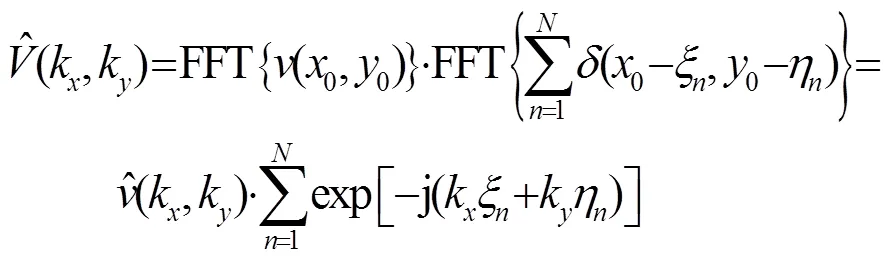
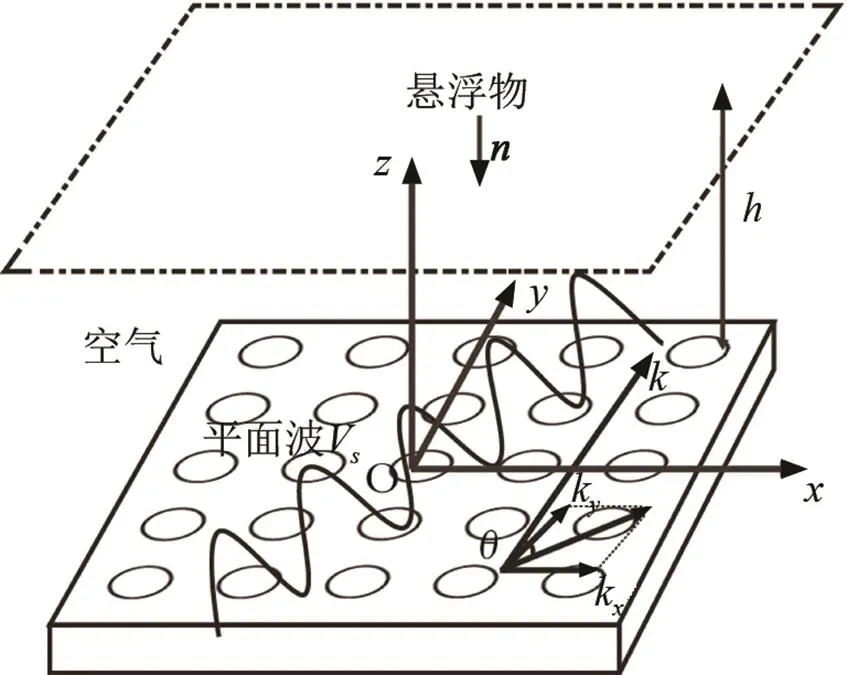
图 2 平面物体的声悬浮

由角谱理论可知，任意声场可以分解成一系列振幅不同的平面声波[3]：

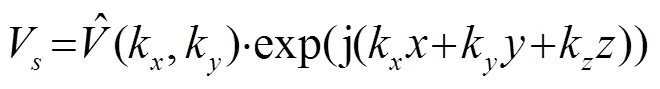
现只取其中的一束平面声波进行分析，由图2可以看出，该平面声波的入射角为

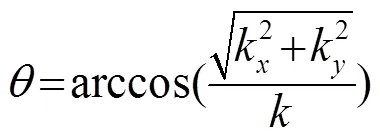
假设该束平面声波遇到上方无限大的平面物体，在物体下表面发生全反射，那么换能器阵和悬浮物之间的声场速度可以表示为

由换能器阵表面的速度边界条件：

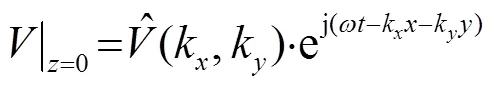
将式(11)代入式(10)，可以得到声场速度表达式：

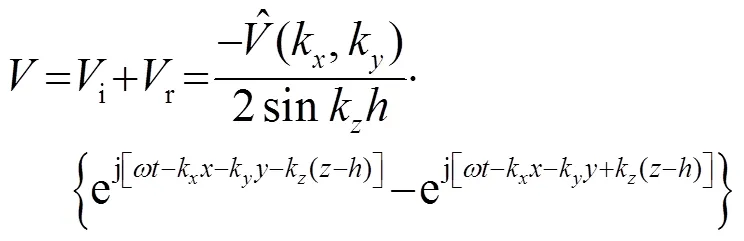
式(12)中，下角i和r分别代表入射和反射平面波。对于平面行波，作用在物体上的声辐射力可以由式(13)给出[6]：

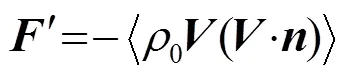
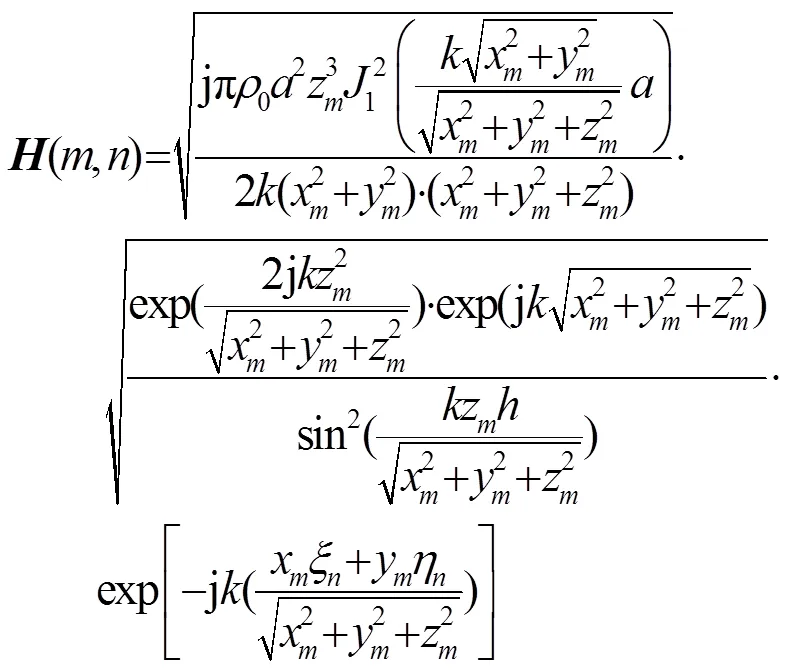
由于系统的对称性，平面悬浮物体所受到的和方向的声辐射力合力为零，故本文只考虑竖直方向上的声辐射力。将式(12)代入式(13)，可求出由角谱法展开的单束平面声波作用在平面悬浮物上，声辐射力在方向上的分量为

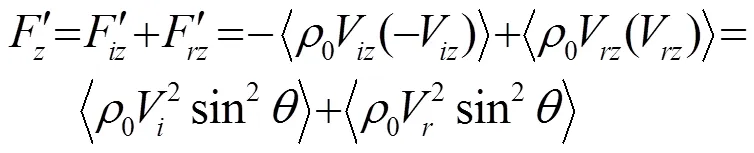
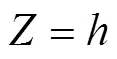
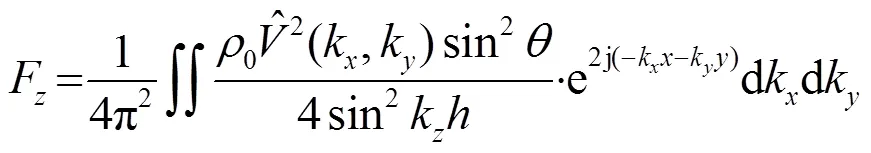
角谱法表示的积分即式(15)一般情况下很少有精确解，一般都采用数值算法进行计算，但是当声波频率比较高时，被积函数震荡剧烈，积分步长不合适会引入很大的误差，故本文采用最快速下降法[7]来进行计算，积分渐近公式为

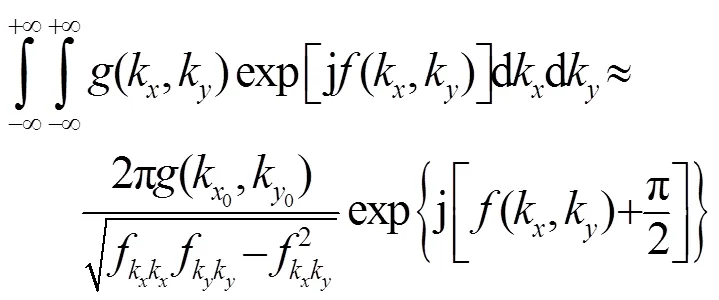
比较式(15)和式(16)可知，

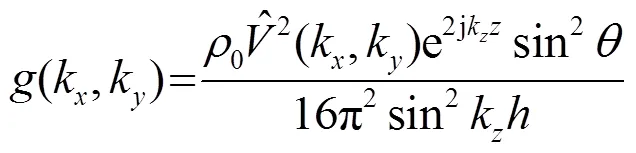
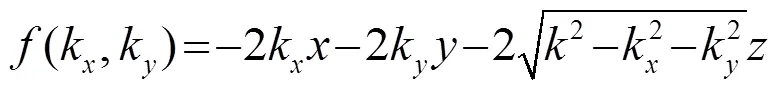
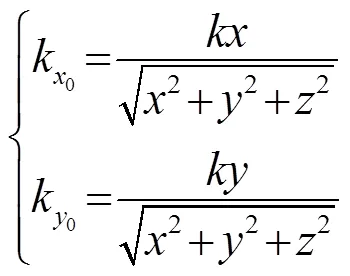
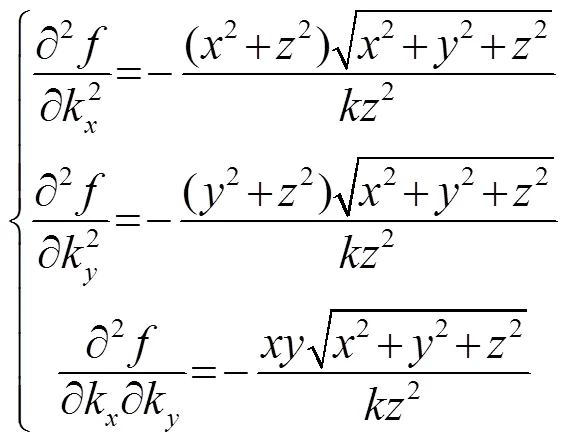
将式(17)～(20)代入式(16)中并化简，可近似求出换能器组阵以后作用在平面悬浮物上的声辐射力分布：

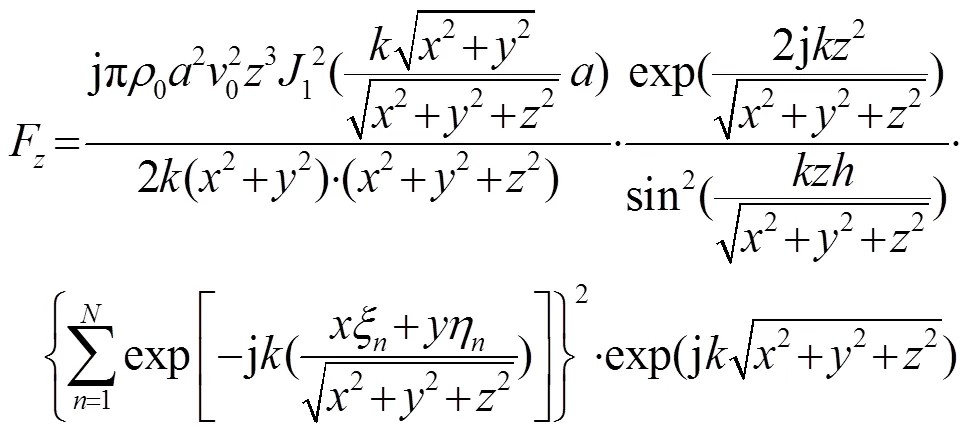
2 声辐射力分布的计算与分析

通过以上对换能器组阵以后作用在平面悬浮物上声辐射力分布公式的推导，本文以MATLAB为编程工具，对作用在平面悬浮物上声辐射力分布进行计算仿真，分析换能器频率、阵元间距、阵元数目对声辐射力分布的影响。在仿真过程中，假设空气为理想介质，并取圆形活塞换能器半径=0.008 m，悬浮物体悬浮高度=0.01 m，阵列排列形式如图1所示。为了方便观察，声辐射力分布皆取在平面(见图2)上进行分析。

2.1 频率对声辐射力分布的影响

由式(21)可知，考虑不同频率的换能器组阵对声辐射力分布的影响。在矩形3×3排列、阵元间距=0.020 m的换能器阵情况下，分别取换能器频率为5 kHz、10 kHz、20 kHz经过仿真得到的声辐射力分布如图3所示。

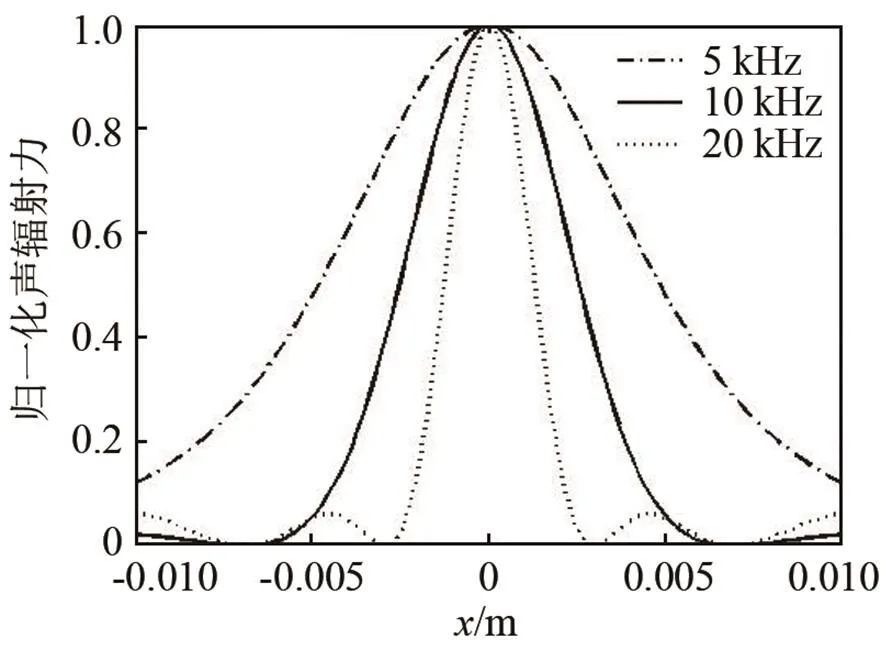
图3 声辐射力分布与频率的变化关系

通过图3显然可以看出，提高换能器的频率，作用在平面悬浮物体上的声辐射力分布指向性变强，主瓣越来越尖锐。

2.2 阵元间距对声辐射力分布的影响

保持换能器阵元频率为20 kHz且换能器阵为矩形3×3排列不变，由式(21)分别计算矩形换能器阵列的阵元间距=0.020，0.024，0.028时，声辐射力分布情况如图4所示。可以看出，随着阵元间距的增加，换能器阵总体尺寸变大，声辐射力分布的主瓣变得尖锐，指向性增强。但是阵元间距的增加会导致整个换能器阵列的单位面积的有效振动面积减小，旁瓣不能得到有效抑制。

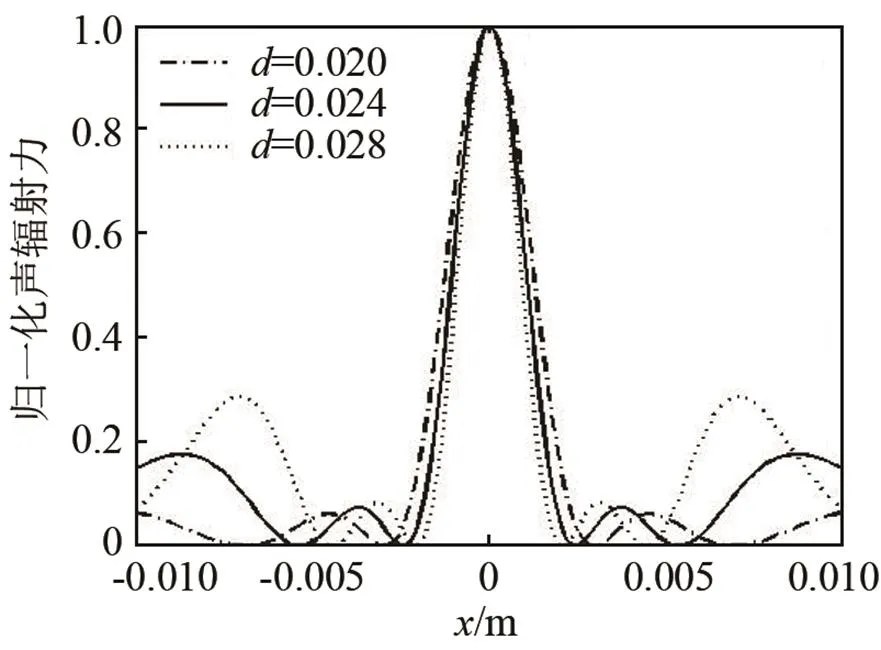
图4 声辐射力分布与阵元间距的变化关系

此外，由于圆形换能器的频率固定，声波在特定的介质中传播的波长也是一定的，所以通常把/作为整体变量来研究阵元间距对指向性的影响。

当换能器的频率为20 kHz时，对应的波长为0.017 m，考虑到圆形换能器尺寸的影响，本文接下来分别取/=1.5，2.5，3.5，来考虑/与声辐射力分布旁瓣的关系，如图5所示。

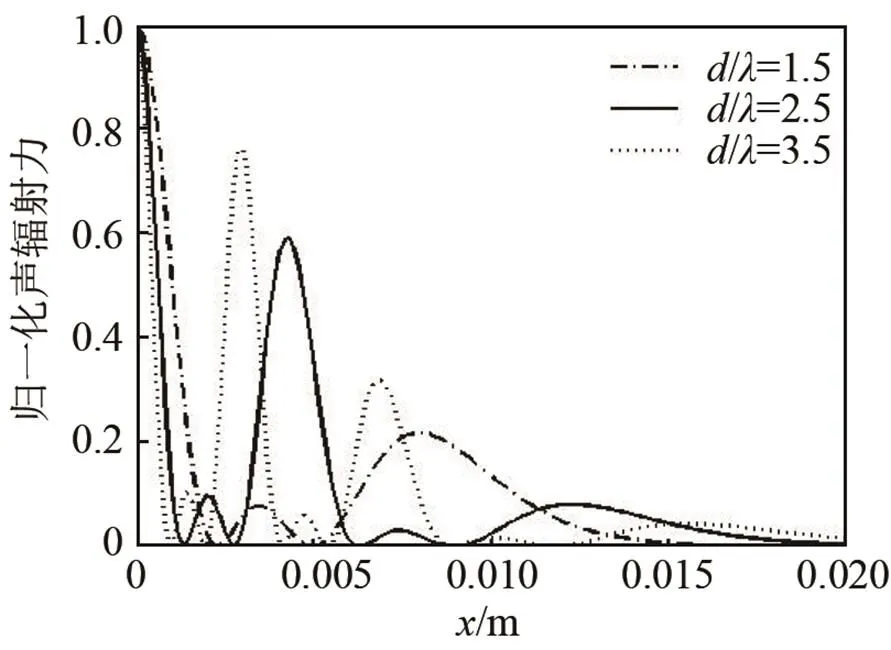
图 5 声辐射力分布与d/λ的关系

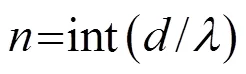
2.3 阵元数目对声辐射力分布的影响

同样保持换能器阵元的频率为20 kHz，阵元间距0.020 m，换能器阵列分别为3×3，5×5，7×7排列，用式(21)仿真分析阵元数目对声辐射力分布的影响。通过仿真分析得到作用在平面悬浮物体上声辐射力分布随阵元数目的变化规律，如图6所示。

从图6中可以看出，随着换能器数目的增加，声辐射力的分布的指向性越来越尖锐而且旁瓣也得到了有效地抑制。所以，应在条件允许的情况下尽可能地增加换能器阵元的数目。

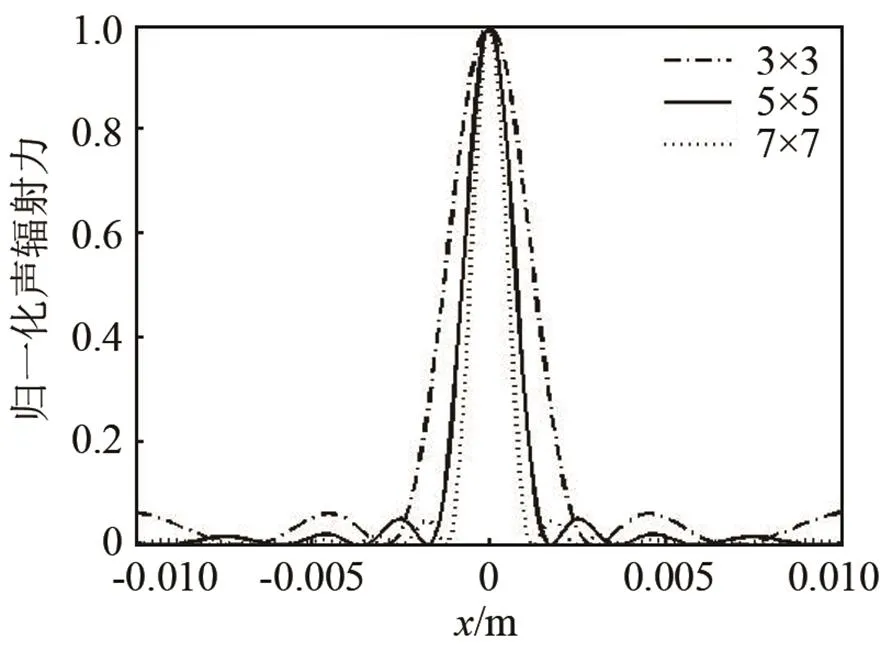
图 6 声辐射力分布与阵元数目的变化关系

3 声辐射力分布的空间调控

由以上对换能器组阵以后作用在平面悬浮物上声辐射力分布的分析可知，换能器数目越多，辐射的声能量越大，能够产生的声辐射力也越大。但是随着换能器阵列阵元数目的增加，声场的指向性增强，声辐射力也会向中间聚集，导致声悬浮不稳定。为了提高声悬浮的稳定性，本文用伪逆矩阵算法合成多焦点声场的相关理论[8]来调节换能器阵元表面振动速度的幅值和相位，从而调控声辐射力的空间分布。

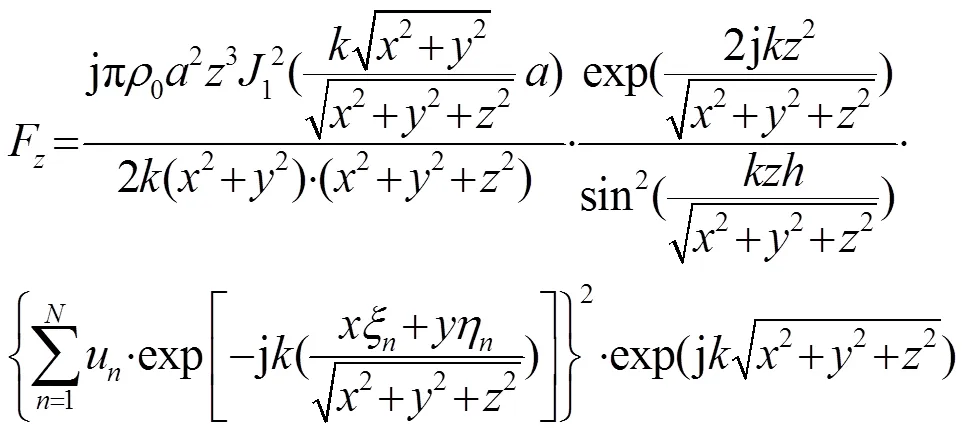
不妨取：

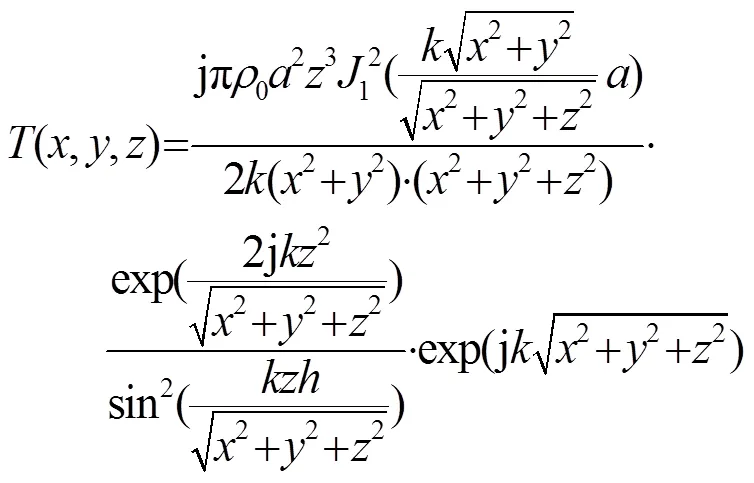
那么，式(22)可以表示为

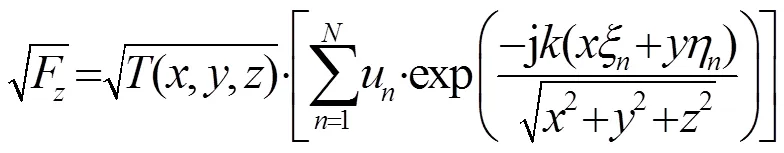
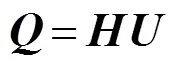
当换能器数目大于控制点的数目时，换能器阵元的复表面振动速度向量可以用伪逆矩阵来表示，表达式为

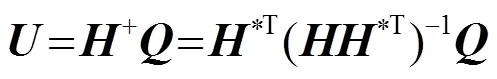
为了调控空间声辐射力的分布，实现稳定的声悬浮，在悬浮物体底面设定多个幅值相同的控制点，使得声辐射力在这些控制点处“聚焦”。因此，就要求换能器阵产生的能量主要用于在控制点处产生足够大的声辐射力，而在其他位置产生的声辐射力很小。

换能器阵产生的总声能量为

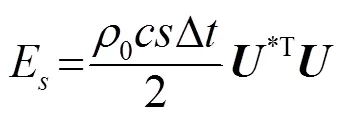
当物体稳定悬浮时，控制点处声辐射力相对于其它位置足够的大，可以认为悬浮物仅仅是由控制点处的声辐射力支撑，那么悬浮物体的重力势能可以表示为

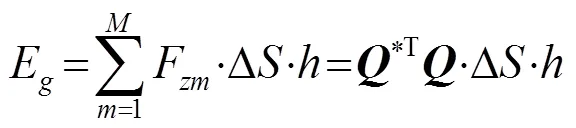
本文引入能量增益的定义如下[9]：

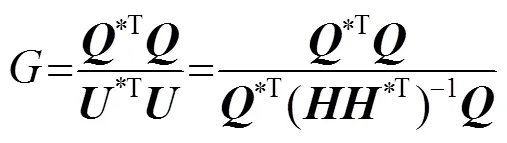
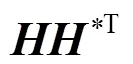
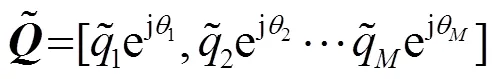
此时，能量增益为

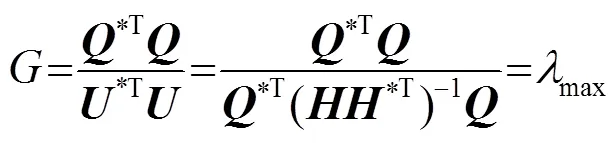
将式(31)代入(27)，即可求出每一个换能器阵元的复表面振动速度。将求出的每个阵元的复表面振动速度代入式(22)，即可得到调控以后的声辐射力分布。

4 声辐射力分布的空间调控算例

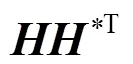
当然，还可以根据平面悬浮物体的尺寸，适当增加焦点的数量或者调节焦点的位置。比如可以产生如图8所示的以边长为0.04 m的正方形和边长为0.12 m的正方形的顶点为控制点的8焦点声辐射力分布，能够实现更稳定的声悬浮。

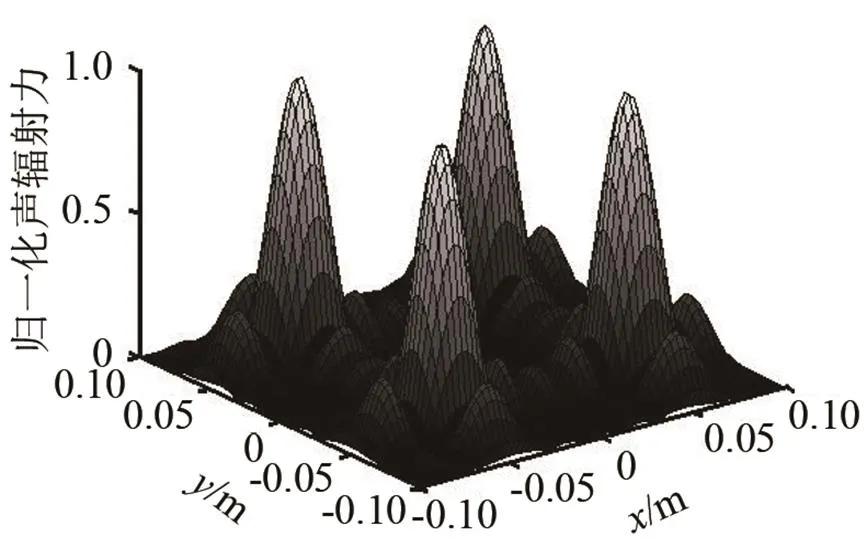
图7 四个焦点的声辐射力分布

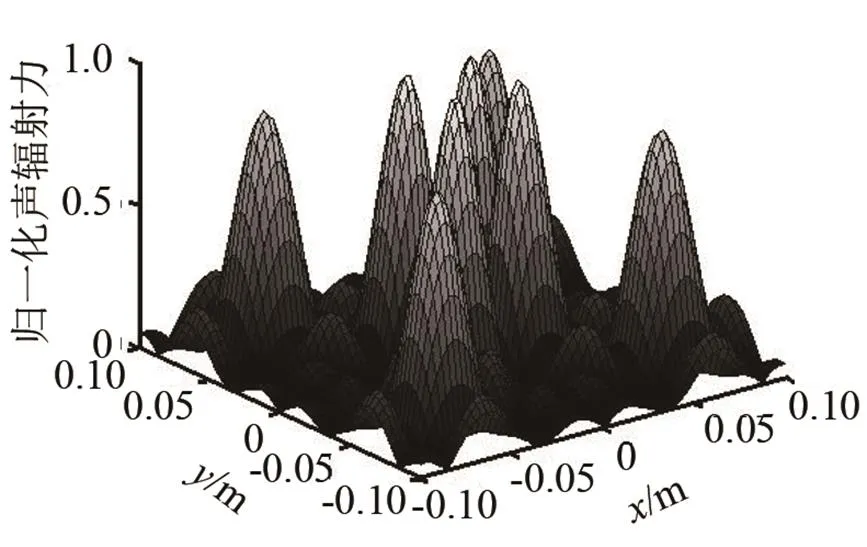
图 8 八个焦点的声辐射力分布

5 结论

本文运用角谱理论对换能器组阵后作用在平面悬浮物体上的声辐射力分布公式进行推导，并且分析了换能器频率、阵元间距以及阵元数目对声辐射力分布的影响，得到了以下结论：

(1)换能器频率的提高，阵元间距以及阵元数目的增加，都会导致作用在平面悬浮物体上的声辐射力分布的主瓣更加尖锐；但是增大阵元间距会使得对声辐射力分布的旁瓣抑制效果减弱；

(2)通过伪逆矩阵算法，以能量增益为目标来调节换能器阵元的振幅和相位，可以形成多焦点的声辐射力分布，为阵列换能器声辐射力分布的空间调控和声悬浮稳定性研究提供了新思路。

[1] GENG G L, XIE W J, WEI B. Containerless solidification of acoustically levitated Ni-Sn eutectic alloy[J]. Applied Physics A, 2012, 109(1): 239-244.

[2] ZHAO S, WALLASCHEK J. A standing wave acoustic levitation system for large planar objects[J]. Arch. Appl. Mech., 2011, 81(2): 123-139.

[3] SAPOZHNIKOV O A, BAILEY M R. Radiation force of an arbitrary acoustic beam on an elastic sphere in a fluid [J]. Acoust. Soc. Am., 2013, 133(2): 661-676.

[4] 丁辉. 计算超声学: 声场分析及应用[M]. 北京: 科学出版社, 2010.

DING Hui. Computational ultrasonics: anslysis and application of ultrasonic field[M]. Beijing: Science Press, 2010.

[5] 吕乃光. 傅里叶光学[M]. 北京: 机械工业出版社, 2016.

LÜ Naiguang. Fourier optics[M]. Beijing: China Mechine Press, 2016.

[6] 李太宝. 计算声学: 声场的方程和计算方法[M]. 北京: 科学出版社, 2005.

LI Taibao. Computational acoustics: equation and computational method of sound field[M]. Beijing: Science Press, 2005.

[7] 羊国光, 宋菲君. 高等物理光学[M]. 合肥: 中国科学技术大学出版社, 2008.

YANG Guoguang, SONG Feijun. Advanced physics optics[M]. Hefei: University of Science and Technology of China Press, 2008.

[8] 施克仁, 郭寓岷. 相控阵超声成像检测[M]. 北京: 高等教育出版社, 2010.

SHI Keren, GUO Yumin. Phased array ultrasonic imaging and testing[M]. Beijing: China Higher Education Press, 2010.

[9] 宋蕊, 张明, 吴成国, 等. 次声相控阵列的聚焦特性研究[J]. 声学技术, 2017, 36(1): 6-9.

SONG Rui, ZHANG Ming, WU Chengguo, et al. Research on the infrasound focusing properties of phased arrays[J]. Technical Acoustics, 2017, 36(1): 6-9.

[10] LONG B, SEAH S A, CARTER T, et al. Rendering volumetric haptic shapes in mid-air using ultrasound[J]. ACM Transactions on Graphics, 2014, 33(6): 1-10.

[11] 徐丰, 万明习, 陆明珠. 遗传算法在256阵元相控阵高强度聚焦超声治疗系统多焦点控制中的应用[J]. 生物医学工程学杂志, 2008, 25(5): 1093-1097.

XU Feng, WAN Mingxi, LU Mingzhu. Genetic algorithm application to multi-focus patterns of 256-element phased array for focused ultrasound surgery[J]. Journal of Biomedical Engineering, 2008, 25(5): 1093-1097.

Calculation and analysis of acoustic radiation force distribution of a two-dimensional transducer array

XU Jia-xin, MA Jian-min

(Department of Aeronautics and Astronautics, Fudan University, Shanghai 200433, China)

According to angular spectrum theory, the distribution of acoustic radiation force acting on the planar levitation object is derived. Through numerical simulation, the influence of transducer frequency, element spacing and the number of elements on the acoustic radiation force distribution is analyzed. The analysis result shows that the transducer array enhances the intensity and directivity of acoustic radiation force; with the increases of frequency, element spacing and the number of array elements, the main lobe of acoustic radiation force distribution becomes sharper. However, increasing element spacing will raise sidelobes of acoustic radiation force distribution. In order to improve space distribution of acoustic radiation force and to form multi-focus acoustic radiation force distribution, the amplitude and phase of the each element are adjusted by using the pseudo inverse matrix algorithm and choosing sound intensity gain as the objective function. It provides help for regulating the distribution of acoustic radiation force and for the study of acoustic levitation stability.

transducer array; angular spectrum theory; acoustic radiation force distribution; spatial regulation

TB559

A

1000-3630(2018)-04-0398-06

10.16300/j.cnki.1000-3630.2018.04.018

2017-07-13;

2017-10-18

徐佳新(1994－), 男, 江苏南通人, 硕士研究生, 研究方向为声波辐射及其控制。

马建敏, E-mail: jmma@fudan.edu.cn