海上多层稠油聚合物驱产液指数变化主控因素

未志杰，康晓东，何春百，张 健，盛 寒

（1.海洋石油高效开发国家重点实验室，北京100028；2.中海油研究总院有限责任公司，北京 100028；3.中海油能源发展股份有限公司 工程技术分公司，天津 300452）

海上油田聚合物驱开发具有多层合采、渗透率级差大、原油黏度大和注聚合物时机早的特点[1]。由于聚合物溶液属于高黏非牛顿流体，且驱替前缘易形成富（稠）油带，明显提高了地层流体渗流阻力，导致部分井产液能力较水驱阶段明显下降[2-3]；同时海上油田注聚合物时机较早，聚合物驱过程中含水率较水驱阶段下降幅度较小或上升速度趋缓[4-5]，这与高含水期注聚合物有显著区别[6-7]。因此，聚合物驱阶段产液能力变化对海上稠油油田高产稳产具有更为重要的意义。

产液指数或无因次产液指数是衡量产液能力的重要指标，目前产液指数的研究方法主要包括矿场动态资料分析[8-11]、渗流力学理论计算[12-14]以及数值模拟[15-17]，但是均存在一定局限性。矿场动态资料分析方法适用于老油田，计算结果反映油田开发过程中各种动、静态因素对产液指数的综合作用，难以甄别不同因素的影响，更难以对其影响的程度作出评估，且该方法对动态监测资料要求高，而海上油田监测数据相对有限；渗流力学理论计算方法目前不考虑储集层非均质性，适用于单层单井的情况，所能考察的因素受限；数值模拟方法需要借助专业软件，且计算过程繁琐，目前仅针对水驱形成了典型通用产液指数计算公式，尚未见关于聚合物驱与后续水驱阶段的系统研究报道。本文基于多相渗流力学理论，构建非均质油藏聚合物驱产液指数计算模型，给出水驱阶段、聚合物驱阶段以及后续水驱阶段产液指数的计算方法，进一步拓展现有方法的适用范围。同时，结合海上典型注聚合物油田特点，开展聚合物驱产液指数变化主控因素研究，以期为稠油聚合物驱持续高效开发提供技术指导。

1 多层油藏聚合物驱产液指数计算模型

1.1 油井控制区渗流阻力

定义渗流阻力为驱动单位流量液体通过多孔介质时所需的压力差，根据达西定律，渗流阻力可表示为

产液指数实质上反映的是油井控制区域内油水综合渗流阻力，渗流阻力越大，产液指数越小；由（1）式可知，产液指数的影响因素包括渗透率、地层几何参数（如泄流面积和井距）等静态因素，以及油水相对渗透率、油水黏度、聚合物黏度等动态因素。无因次产液指数，即某一时刻产液指数与初始时刻产液指数的比值，消除了静态因素的影响。

一般而言，储集层含水饱和度、聚合物质量浓度等在注入井与采油井之间存在空间变化，越靠近采油井值越低，且该空间分布随驱替的进行而发生变化，造成油井控制区渗流阻力存在时空差异。为客观表征产液能力，需要研究油井控制区整体渗流阻力在驱替过程中的变化情况，将注采井间靠近采油井的一半区域作为油井控制区，整体渗流阻力表达式为

1.2 多层油藏渗流阻力方程

对于多层非均质储集层，油井控制区整体渗流阻力可表示为

下面推导第i层渗流阻力Rˉi的计算方程。油田开发过程一般包括水驱、聚合物驱以及后续水驱阶段。根据渗流力学理论，结合Buckley-Leverett公式[18-19]，推导了这3个阶段Rˉi的计算方程。

1.2.1 水驱阶段

由Buckley-Leverett公式[18-19]，第i层注入流体波及区连续性方程满足：

给定相渗曲线和油水黏度，则油水总流度是含水饱和度的函数λTi=λwi+λoi=g(Swi)；且含水饱和度是分流量导数的单调函数，即Swi=h(f'wi)；故油水总流度可表示为分流量导数的函数：

若注入水已经在采油井端突破，将（6）式和（7）式代入（2）式，则：

由（8）式和（9）式可以看出，油井控制区渗流阻力仅与该层累计注入孔隙体积倍数有关。

1.2.2 聚合物驱阶段

同理，也可以推导出聚合物驱阶段的渗流阻力为前置水驱段累计注入量Qwi和聚合物注入量Qpi的函数。

1.2.3 后续水驱阶段

后续水驱阶段的渗流阻力为水驱段累计注入量Qw1i，聚合物段累计注入量Qpi和后续水驱注入量Qw2i的函数。

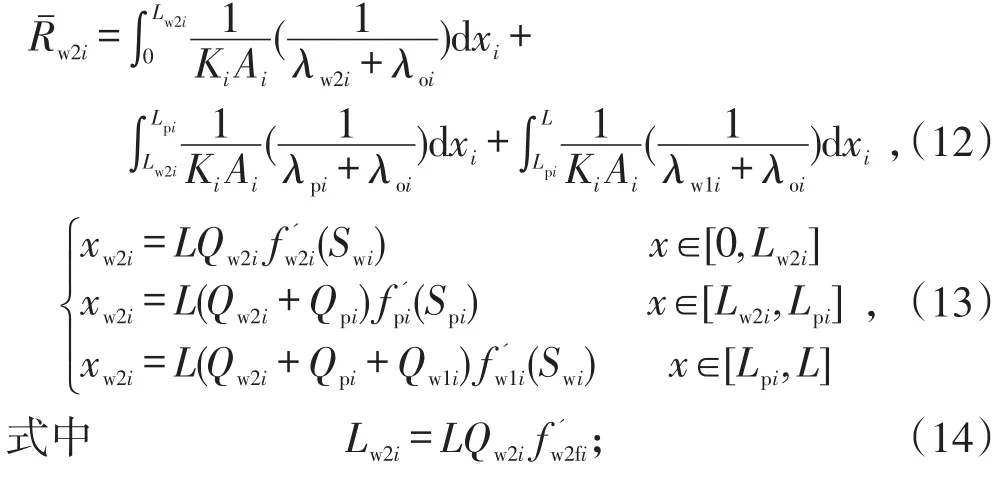
由上述推导可知，第i层渗流阻力仅与该层累计注入孔隙体积倍数有关，即：

1.2.4 约束方程

各层累计注入孔隙体积，即总注入量在各层的分配情况，通过求解物质守恒方程获得：

根据所构建的聚合物驱产液指数计算模型，采用Matlab编制了求解程序，并通过与室内实验结果对比验证其准确性，结果表明两者的产液指数相对偏差在5.0%以内。

2 聚合物驱产液指数主控因素

为了便于研究，简化问题，参考渤海SZ油田数据，建立典型模型：①双层层状油藏，行列式井网，井距300 m，垂向有效厚度均为15 m；②压力、体积、温度、相对渗透率曲线等岩石流体数据采用油田实际数据，地层原油黏度70.0 mPa·s；③渗透率分别为500 mD和2 000 mD，渗透率级差为4；④驱替过程，先水驱至含水率达到70%，然后转聚合物驱；⑤注入聚合物的质量浓度为1 750 mg/L，地下黏度约为6.5 mPa·s，残余阻力系数为1.6，不可及孔隙体积数为0.18.

2.1 变化特征

注入过程中无因次产液指数变化情况如图1所示，水驱阶段产液指数在见水后不断上升，而聚合物驱阶段呈“四段式”变化：①上升段，聚合物注入初期，对控制区的影响有限，渗流阻力延续之前水驱阶段的下降趋势（图1），故而产液指数继续上升，含水率上升，但增长趋缓；②下降段，随着聚合物的注入，前缘逐步形成富油带，当富油带进入控制区但未在采油井突破时，稠油饱和度升高，渗流阻力迅速上升，含水率缓慢下降，产液指数快速下降；③平稳段，富油带突破后，含水率显著下降，但控制区内含油饱和度较高，渗流阻力逐步达到最大并维持在较高水平，相应的产液指数保持平稳；④回升段，随着富油带全部突破，含聚合物水相对渗流阻力的贡献逐渐占优势，含水率持续上升，渗流阻力不断下降，产液指数回升。

为定量刻画聚合物驱无因次产液指数的变化，引入无因次产液指数最大降幅DJ和波谷时机Dt：最大降幅DJ是指无因次产液指数最低值NJmin相比转注聚合物时刻无因次产液指数值NJmax，wf的相对下降幅度（图2）；波谷时机Dt是指无因次产液指数达到最低值时所对应的聚合物注入孔隙体积倍数。图2中无因次产液指数最低值为1.49，转注聚合物时为3.17，最大降幅为53.1%，波谷时机为0.250 PV.

图1 注入过程中渗流阻力和含水率变化情况

图2 注入过程中无因次产液指数变化情况

2.2 参数敏感性分析

根据多层油藏聚合物驱产液指数计算模型，产液指数的影响因素包括原油黏度、聚合物黏度、注聚合物时机、渗透率级差、高渗层与低渗层孔隙度比、低渗层相对厚度、聚合物地层吸附能力以及聚合物残余阻力系数8个因素，其中低渗层相对厚度采用低渗层与高渗层厚度比来表示。影响因素多且复杂，为了快速确定影响海上稠油油田无因次产液指数的关键参数，采用单因素分析法开展了参数敏感性研究，并选取无因次产液指数波谷时机和最大降幅作为分析指标。

结合SZ油田油藏地质条件及聚合物物化属性数据，确定了上述8个影响因素的变化范围，原油黏度30.0～150.0 mPa·s，聚合物黏度2.5～10.0 mPa·s，注聚合物时机对应含水率0.5～0.9，渗透率级差2～8，高渗层与低渗层孔隙度比1.0～1.6，低渗层与高渗层厚度比0.5～2.0，聚合物地层吸附能力倍数0.5～1.5，聚合物残余阻力系数1.2～2.0.

在原油黏度70.0 mPa·s，聚合物黏度6.5 mPa·s，注聚合物时机对应含水率0.7，渗透率级差4，高渗层与低渗层孔隙度比1.2，低渗层与高渗层厚度比1.0，聚合物地层吸附能力倍数1.0，聚合物残余阻力系数1.6（基础方案）条件下，无因次产液指数波谷时机为0.250 PV，最大降幅为53.1%.固定其他影响因素值不变，依次分别改变各影响因素值至最小值和最大值，计算相应的波谷时机和最大降幅，并计算了相对基础方案时的偏差程度（表1）。

敏感性判断标准采用拇指法则，即相对偏差值大于10%的作为敏感参数。从表1可知，波谷时机的敏感参数包括原油黏度、渗透率级差、低渗层与高渗层厚度比以及聚合物地层吸附能力倍数，无因次产液指数最大降幅的敏感参数包括聚合物黏度、注聚合物时机以及渗透率级差。波谷时机和最大降幅的敏感参数不完全相同。值得注意的是，当前算例下，原油黏度对无因次产液指数最大降幅的影响不显著，注聚合物时机对应含水率对无因次产液指数波谷时机的影响不显著。

表1 不同影响因素下无因次产液指数最大降幅和波谷时机的计算结果

2.3 波谷时机和最大降幅计算公式

影响无因次产液指数最大降幅及波谷时机的关键因素较多，计算相对复杂，为便于油藏工程分析，基于均匀设计方法，建立了经验模型。首先采用基于全局寻优的多因素均匀设计方法设计若干实验方案；之后运用所提出的多层油藏聚合物驱产液指数模型，获得各方案的波谷时机和最大降幅；最后进行多因素回归分析，建立产液能力特征量计算模型。

选取均匀设计表U*12(1210)[20]，使用设计表第1列、第6列、第7列和第9列设计波谷时机实验方案，第1列、第6列和第9列设计无因次产液指数最大降幅实验方案。结合上述SZ油田储集层及流体物化参数，设计了各敏感参数不同水平组合方案，并计算得到了相应的无因次产液指数最大降幅和波谷时机（表2，表3）。

表2 无因次产液指数最大降幅预测均匀设计实验方案

根据表2和表3中的数据，回归分析得到了无因次产液指数波谷时机和最大降幅。

在各敏感参数的变化范围内，无因次产液指数最大降幅为37.9%～70.4%，平均为53.1%；波谷时机为0.068～0.371 PV，平均为0.250 PV.

2.4 实例应用

将产液指数最大降幅经验模型应用于海上SZ油田产液能力研究，该油田聚合物驱试验区目前累计注入聚合物0.42 PV，处于产液能力回升期。生产统计数据表明，无因次产液指数最大降幅为36.3%～64.8%，平均为52.0%；计算无因次产液指数最大降幅为36.2%～66.3%，平均为53.0%；绝对偏差为-0.8%～2.9%，平均为1.0%（表4）。

表3 无因次产液指数波谷时机预测均匀设计实验方案

3 结论

（1）建立了基于Buckley-Leverett公式的多层油藏聚合物驱产液指数计算模型，进一步拓展并完善了现有产液指数计算方法。

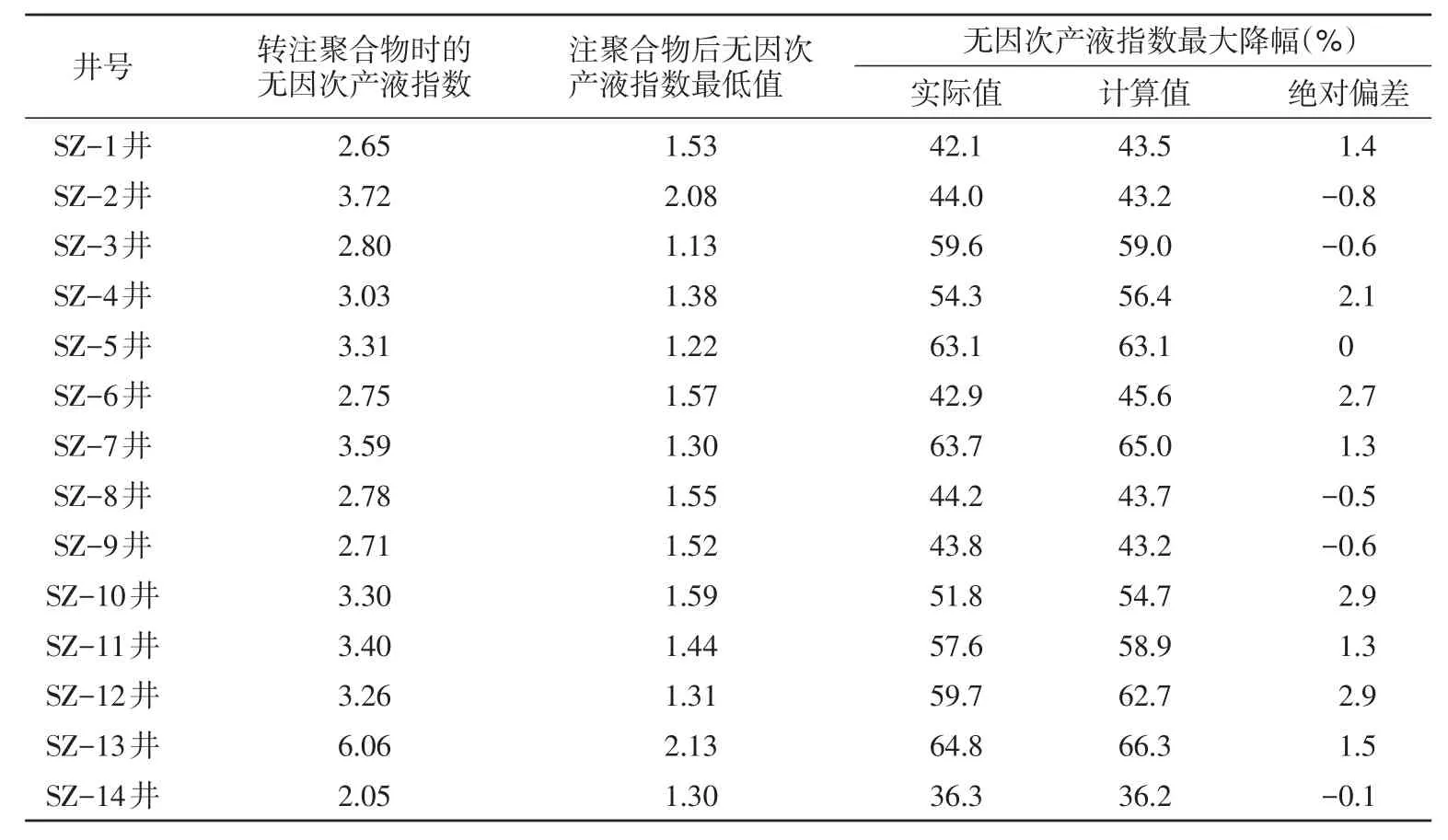
表4 SZ油田无因次产液指数最大降幅计算值与实际值对比

（2）产液指数在转注聚合物后依次经历上升段、下降段、平稳段和回升段，整体呈现“四段式”变化特征。

（3）无因次产液指数最大降幅的主控因素包括聚合物黏度、注聚合物时机以及渗透率级差，波谷时机的主控因素包括原油黏度、渗透率级差、低渗层与高渗层厚度比以及聚合物地层吸附能力倍数。原油黏度对产液指数最大降幅的影响不显著，注聚合物时机对波谷时机的影响不显著。

（4）基于多因素均匀设计方法，进一步提出了无因次产液指数最大降幅及波谷时机计算公式，可方便应用于油藏工程分析。

（5）海上典型注聚合物油田条件下，无因次产液指数最大降幅为37.9%～70.4%，平均为53.1%；波谷时机为0.068～0.371 PV，平均为0.250 PV.

符号注释

A——渗流截面积，m2；

d——差分函数；

DJ——无因次产液指数最大降幅，%；

Dt——波谷时机，定义为无因次产液指数达到最低值时对应的注入聚合物孔隙体积倍数，PV；

Fw——注聚合物时机，用转注聚合物时的含水率表示；

g（Swi）——总流度关于含水饱和度的函数；

h——储集层厚度，m；

i，j——储集层编号；

J——产液指数，m3/（Pa·s）；

JD——无因次产液指数；

K——渗透率，mD；

Kro——油相相对渗透率；

Krw——水相相对渗透率；

L——注采井间距离，m；

Lpi——第i层聚合物推进前沿位置，m；

Lw2i——第i层后续水驱推进前沿位置，m；

n（Qi）——第i层油井控制区整体渗流阻力关于注入孔隙体积倍数的函数；

N——储集层总数；

p——压力差，Pa；

pi——初时时刻压力差，Pa；

pe——地层静压，Pa；

pet——t时刻地层静压，Pa；

pwf——油井流压，Pa；

pwfi——初时时刻油井流压，Pa；

pwft——t时刻油井流压，Pa；

ql——地层流体流量，m3/s；

qli——初时时刻地层流体流量，m3/s；

qlt——t时刻地层流体流量，m3/s；

qinj——注入量，m3/s；

Qi——第i层累计注入孔隙体积倍数，PV；

Qpi——第i层累计注入聚合物孔隙体积倍数，PV；

Qwi——第i层累计注入孔隙体积倍数，PV；

Qw1i——第i层前置水驱累计注水孔隙体积倍数，PV；

Qw2i——第i层后续水驱累计注水孔隙体积倍数，PV；

R——渗流阻力，Pa·s/m3；

Rˉ——整体渗流阻力，Pa·s/m3；

Rad——聚合物地层吸附能力倍数；

RH——低渗层与高渗层厚度比；

Rˉi——初时时刻整体渗流阻力，Pa·s/m3；

Rˉi——第i层渗流阻力，Pa·s/m3；

R͂i——第i层注采井间的渗流阻力，Pa·s/m3；

RK——渗透率级差；

Rp——聚合物与地层水黏度比；

Rμ——原油黏度与地层水黏度比值；

Swi——含水饱和度；

t——开发时间，s；

Vpvi——第 i层孔隙体积，m3；

x——沿程距离，m；

xpi——聚合物驱阶段第i层注入流体波及区内的沿程距离，m；

xwi——水驱阶段第i层注入流体波及区内的沿程距离，m；

xw2i——后续水驱阶段第i层注入流体波及区内的沿程距离，m；

xwfi——第i层水驱推进前沿位置，m；

λoi——第i层油相流度，（mPa·s）-1；

λpi——第i层聚合物流度，（mPa·s）-1；

λTi——第i层油水总流度，（mPa·s）-1；

λwi——第i层水相流度，（mPa·s）-1；

λw1i——第i层前置水驱段水相流度，（mPa·s）-1；

λw2i——第i层后续水驱段水相流度，（mPa·s）-1；

λwpi——第i层水或聚合物流度，（mPa·s）-1；

μo——原油黏度，mPa·s；

μw——地层水黏度，mPa·s；

ϕ——孔隙度。