需求响应式公交乘客出行中心确认方法研究
阮冠轩, 靳文舟, 韩博文
(华南理工大学 土木与交通学院, 广东 广州 510641)
与传统的接驳公交相比,需求响应式公交(demand responsive transit,简称为DRT)站点和路线随着乘客需求位置的变化而变化。Dagenzo[1]首次提出并证明了DRT在低人口出行区域内能够比常规公交提供更为高效的服务。Rodier[2]等人对于DRT和快速客运等在当时较为超前的公交系统进行了研究,并对各种运输方式进行比较与评估。在该研究中得出的信息服务可以大幅提升乘客的出行收益。Bakker[3]通过分析荷兰低人口密度区域的出租车合乘模式,认为需求响应式的公交服务更适合于这种人口密度区域。Cortes[4]等人对DRT系统进行了模拟,并进行了可行性分析。其研究结果表明:在特定的服务条件和出行量下,DRT的效益将优于常规公交的效益。Bellini[5]等人将系统最优作为目标,以成本、服务水平及环境友好度作为决策变量,提出了一种DRT的车辆调度模型。Li[6]等人通过模拟仿真和理论计算,给出了DRT调度模型和服务区域范围的划分方式。Cremers[7]等人基于Paratransit系统动态规划,提出了使用两阶段调度模型求解DRT并用遗传算法最终求解的方法。
在中国,DRT的研究起步较晚、规模小,未能形成成熟的体系。谢成辉[8]等人提出了DRT系统的构建方案,并指出:很多城市的公交系统合理性不高,并指出:部分公交系统客流较少、企业利益不高、服务水平低,而DRT能够为服务水平低区域的乘客提供较好的公交服务。胡非与[9]等人定义了DRT及其运营过程,明确提出了GPS对DRT所具有的辅助作用,从多角度论证了在中国实行DRT的可行性,提出在运营过程中需要考虑多方面因素,如:票价、时间窗及服务规模等。胡列格[10]等人对于城市定制公交的合乘站点进行了研究。通过K-means算法,建立了公交站点的布局模型。基于支付意愿的DRT,采用干线公交和接驳公交组合调度的运营模式,干线公交的停靠站点为各个区域内的乘客出行中心点。乘客在手机等客户端确认自己的出行地点及支付意愿,系统将会收集乘客信息,并利用接驳公交提供点到点的接送服务,将乘客送至乘客出行中心点,再由干线公交到乘客出行中心点接送乘客,提供长距离出行服务。现有DRT的研究着重点为其适用范围、可行性分析及车辆调度模型等,对DRT的干线公交停靠站点,即接驳公交服务区域内乘客出行中心点和孤立乘客剔除的研究较少,并且均将距离较远或者较孤立的乘客出行点直接当作孤立点处理,没有充分考虑偏远地区有支付意愿乘客的出行需求。作者拟提出一种考虑支付意愿的乘客出行中心点确认方法以及孤立点的剔除方法。
1 传统算法
1.1 欧氏距离的乘客出行中心点和孤立点的确认
欧几里德度量(Euclidean metric)也称为欧氏距离,是一个通常采用的距离定义,指在多维空间中2个点之间的真实距离,或者向量的自然长度(即该点到远点的距离)。在二维或者三维空间中,欧氏距离就是2个点之间的实际距离。
二维空间的计算式为:
distance(欧)=
(1)
采用欧氏距离排除孤立乘客和计算乘客出行中心点的步骤为:
1) 先收集所有乘客出行点的坐标,将所有横、纵坐标分别叠加,然后除以乘客出行总数,得出乘客出行中心点。其表达式为:
(2)
(3)
(4)
2) 计算每一个乘客出行点与乘客出行中心的欧氏距离,剔除掉若干个欧氏距离最大的出行点。
3) 重新计算剩余乘客的出行中心点,并以此作为干线公交的停靠站点。
1.2 马氏距离的乘客出行中心点和孤立点的确认
马氏距离(Mahalanobis distance)是由印度统计学家马哈拉诺比斯(Mahalanobis P C)提出的,计算数据的协方差距离。它是一种有效的计算2个未知样本集的相似度的方法。
马氏距离的计算公式为:
(5)
式中:μ为样本均值。
协方差矩阵的第i,j项的协方差为:
(6)
马氏距离排除孤立乘客和计算乘客出行中心点的步骤为:
1)收集所有乘客出行点的坐标,计算各个乘客出行坐标与出行总体的协方差矩阵,并计算每一个乘客出行点的马氏距离,剔除掉若干个马氏距离大的出行点。
2)重新计算剩余乘客的出行中心点,并以此作为干线公交的停靠站点。
马氏距离和欧氏距离的最大区别在于:欧氏距离仅仅计算出距离最远的点,而马氏距离能充分考虑各个点之间的联系和紧密程度,能计算出点密度最低的点。但是,对于基于支付意愿的需求响应式公交而言,不论欧氏距离还是马氏距离,在确立乘客出行中心点和剔除孤立点乘客时,都存在着不足之处:①乘客出行中心点的确认仅仅依靠乘客出行的地理坐标,没有充分考虑乘客的支付意愿;②在进行孤立点剔除时,仅仅考虑了乘客预定时的地理坐标是否偏远,而没有把乘客的支付意愿纳入到考虑范围内。在基于支付意愿的需求响应式公交中,乘客的支付意愿越高,理应获得更大的被接送的可能。
2 基于重心位置的乘客出行中心点的确认和孤立点的剔除方法
2.1 重心位置的乘客出行中心点的确认
同一平面内,不同地理坐标的乘客有不同的出行支付意愿,这种情况与密度不均匀的铁片十分相似。因此,对于不同出行位置、不同支付意愿的乘客出行,计算其“出行重心”位置更为合理。
密度不均匀铁片重心的计算方法:已知各部分的重心所在位置和质量,选取一个点作为坐标原点,建立直角坐标系,分别计算各部分重心点到x轴和y轴的力矩,分别按照x轴和y轴求和,得到x轴和y轴的总力矩数,除以铁片的总重量,即可得到x轴和y轴的重心坐标。
仿照密度不均匀铁片的重心计算方式,本研究设计了基于重心位置的乘客出行中心点计算方法,其计算式为:
(7)
(8)
center=(xcenter,ycenter)。
(9)
式中:xi是i点乘客的出行点横坐标;yi是i点乘客的出行点纵坐标;Pi为i点乘客的支付意愿。
2.2 重力模型的孤立点乘客算法
不论是欧氏距离还是马氏距离计算的中心点位置,少数的孤立点对中心点位置的影响都是极大的。但欧氏距离和马氏距离在剔除孤立点时均没有考虑乘客的支付意愿,因此,若运用欧氏距离和马氏距离来计算孤立点,对于基于支付意愿的需求响应式公交是不合理的。本研究提出一种基于重力模型的算法,计算每个乘客出行点和乘客出行中心点的吸引力,以此来确认孤立点。
重力模型是交通分布预测中一种最常用的方法,它根据牛顿的万有引力定律,即两物体间的引力与两物体间的质量之积成正比,且与它们之间距离的平方成反比类推而成。
在该模型中,乘客与出行中心的吸引力计算式为:
(10)
式中:gi为i点乘客的吸引力;Pi为i点乘客的支付意愿;P为乘客出行中心点的支付意愿,为一个常数(为便于计算,其值取1);di为i点乘客的出行点到乘客出行中心点的欧氏距离。
2.3 重心模型的计算步骤
1) 收集所有乘客的出行坐标和支付意愿。
2) 根据乘客的出行坐标和支付意愿,计算出行中心点。
3) 计算各个乘客出行点与出行中心点的吸引力,并排除若干个吸引力最小的乘客出行点。
4) 重新计算剩余乘客的出行中心点,并以此作为干线公交的停靠站点。
3 模型的构建及算法设计
本研究将构建接驳公交的调度模型,用于验证作者提出的中心点确认方法及孤立点剔除方法,为接驳公交的运营带来更大的效益。
3.1 模型的构建
以乘客支付意愿收益最大化作为目标函数,构建的车辆调度模型为:
(11)
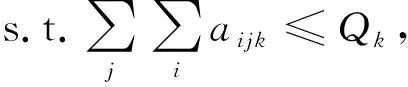
(12)

(13)

(14)
aijk=0或1。
(15)
式中:Pi为i点乘客的支付意愿;Qk为接驳公交的核载量;Lij为i点到j点的距离;Lmax为接驳公交的最大行驶距离;D为乘客预定总数;aijk是决策变量,其值为0或1。
式(11)计算模型的优化目标为乘客支付意愿的最大化;式(12)计算接驳公交k上的乘客总数不大于其核载量;式(13)接驳公交k的行驶距离不得大于其最大行驶距离;式(14)计算被接送的乘客总数不大于其预订数。式(15)计算aijk的取值只能为0或1(当乘客从i点被接驳公交k接送至j点时,aijk为1;否则,aijk为0)。
3.2 算法设计
假设接驳公交规模N、接驳公交核载量Q及接驳公交最大行驶距离Lmax,其计算步骤为:
1) 设定已接送集合set1=[ ],表示没有乘客被接送。设定Nk=0,表示已使用的接驳公交为0。
2) 剔除孤立点乘客,确定乘客出行中心点center;计算剩余的所有乘客出行点彼此之间的吸引力,生成吸引力矩阵。
3) 如果Nk≥N,跳转至2);如果set1集合中包含所有的乘客出行点,跳转至2);否则,找出不在集合set1中且与center吸引力最大的A点,直接与center相连,并将A纳入到set1中。
4) 设定接驳公交车辆k目前的载客量k=1,设定set2为接驳公交k的接送乘客集合,并将A点纳入set2中,索引点Idx=A。
5) 如果k<7,找出不在集合set1中且与索引点Idx吸引力最大的B点。否则,清空set2,Nk=Nk+1,跳转至2)。
6) 计算从center途经set2到达B点,并从B点返回center的距离Lk。如果Lk≤Lmax,将B点纳入set1和set2中,k=k+1,索引点Idx=B,跳转至5);否则,k=k+1,跳转至5)。
7) 结束。
4 算例分析
目前,尚未有开通基于支付意愿的需求响应式公交。因此,本研究通过数值模拟,对比传统的需求响应确认的乘客出行中心点与基于重心吸引力确定的乘客出行中心点的区别。数值模拟数据见表1。
假设接驳公交数量为2辆,核载量为7人,最长行驶距离为2.5 km。孤立乘客的数量为总出行量的10%。

表1 乘客信息Table 1 The passenger information
4.1 欧氏距离乘客出行中心点算法的实验结果
依据欧氏距离,确定乘客出行中心点。经计算,得出初步的乘客出行中心点为(4.08,3.97),各个乘客点与中心点的欧氏距离结果见表2。
根据欧氏距离的大小,确认孤立点乘客为4号和17号。剔除孤立点乘客后,重新计算乘客出行中心点,其坐标为(4,3.99)。中心点位置如图1所示。
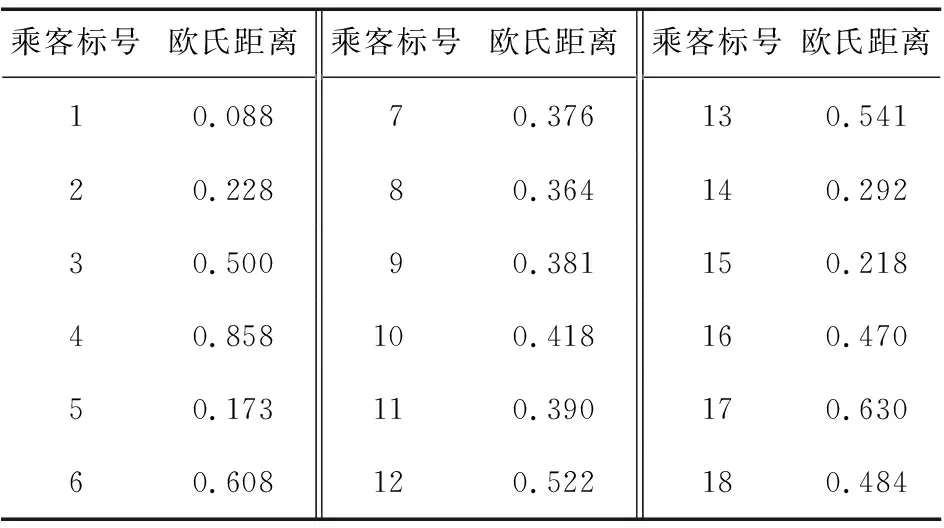
表2 乘客欧氏距离Table 2 Passenger Euclidean distance
最终确认接送13名乘客,接驳巴士1共接送7名乘客,接送的先后顺序为1-2-7-8-3-18-6,接驳公交1行程距离为1.73 km;接驳巴士2共接送6名乘客,接送的先后顺序为5-9-16-14-15-11,接驳公交2行程距离为2.11 km。乘客支付意愿总收益为61元,运行路线如图2所示。

图1 中心点示意Fig. 1 Center point diagram

图2 运行路线Fig. 2 Running road map
4.2 马氏距离乘客出行中心点算法的实验结果
依据马氏距离计算公式,得出18名乘客的马氏距离,其马氏距离见表3。

表3 乘客马氏距离Table 3 Passenger Mahalanobis distance
根据马氏距离的大小,确认的孤立点乘客为4号和13号。剔除孤立点乘客后,计算乘客出行中心点。其坐标为(4.03,3.97),中心点位置如图3所示。

图3 中心点示意Fig. 3 Center point diagram
最终确认接送13名乘客,接驳巴士1共接送7名乘客,接送的先后顺序为1-2-7-8-3-18-6,接驳公交1行程距离为1.73 km;接驳巴士2共接送6名乘客,接送的先后顺序为5-9-16-14-15-11接驳公交2行程距离为2.11 km。乘客支付意愿总收益为61元,运行路线如图4所示。

图4 运行路线Fig. 4 Running road map
4.3 重心位置的乘客出行中心点算法实验结果
根据本研究提出的基于重心位置的乘客出行中心点的确认算法,初步得出的乘客出行中心坐标为(4.13,3.93)。基于重力模型的孤立点乘客算法,计算出18名乘客与乘客出行中心的吸引力系数,见表4。
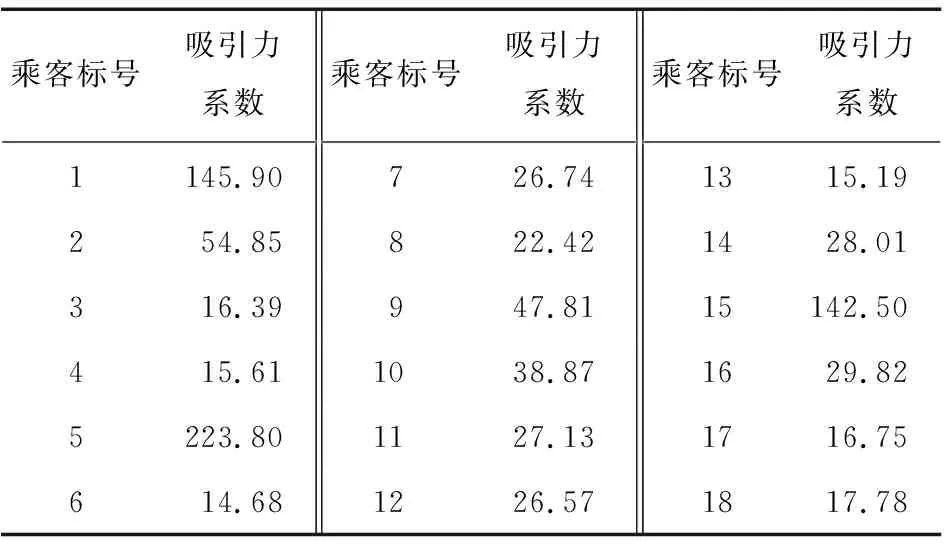
表4 乘客吸引力系数Table 4 Passenger attraction coefficient
根据与乘客出行中心吸引力的大小,最后确认的孤立点乘客为6号和13号。剔除掉孤立点乘客后,对剩余乘客重新计算出行中心,其坐标为(4.17,3.91),中心点位置如图5所示。

图5 中心点示意Fig. 5 Center point diagram
最终确认接送13名乘客,接驳巴士1共接送7名乘客,接送顺序为5-9-16-14-18-3-8,接驳公交1行程距离为1.91 km;接驳巴士2共接送6名乘客,接送顺序为15-11-17-12-10-4,接驳公交2行程距离为2.4 km。乘客支付意愿总收益为70元,运行路线图如图6所示。
4.4 结果分析
在采用相同的路径算法的基础上,采用传统的孤立点剔除方法和中心点确认方法与作者提出的孤立点剔除方法和中心点确认方法相比较。采 用传统算法时,乘客支付意愿收益为61元;采用基于重心位置的算法时,乘客支付意愿收益为70元。在乘客支付意愿收益上,3种乘客中心点算法存在着较大的差异。其原因在于:4号点的乘客虽然位置偏远,但是拥有更迫切的出行需求,其支付意愿也较其他乘客的高。采用传统的孤立点剔除方法,均将4号乘客作为孤立乘客,拒绝了他的出行需求。这并不符合基于支付意愿的需求响应式公交的本质。支付意愿越高的乘客,应该获得更大的被接送的可能。从实验结果可以看出,乘客出行中心的位置,对于最终的乘客支付意愿收益的影响是很大的。
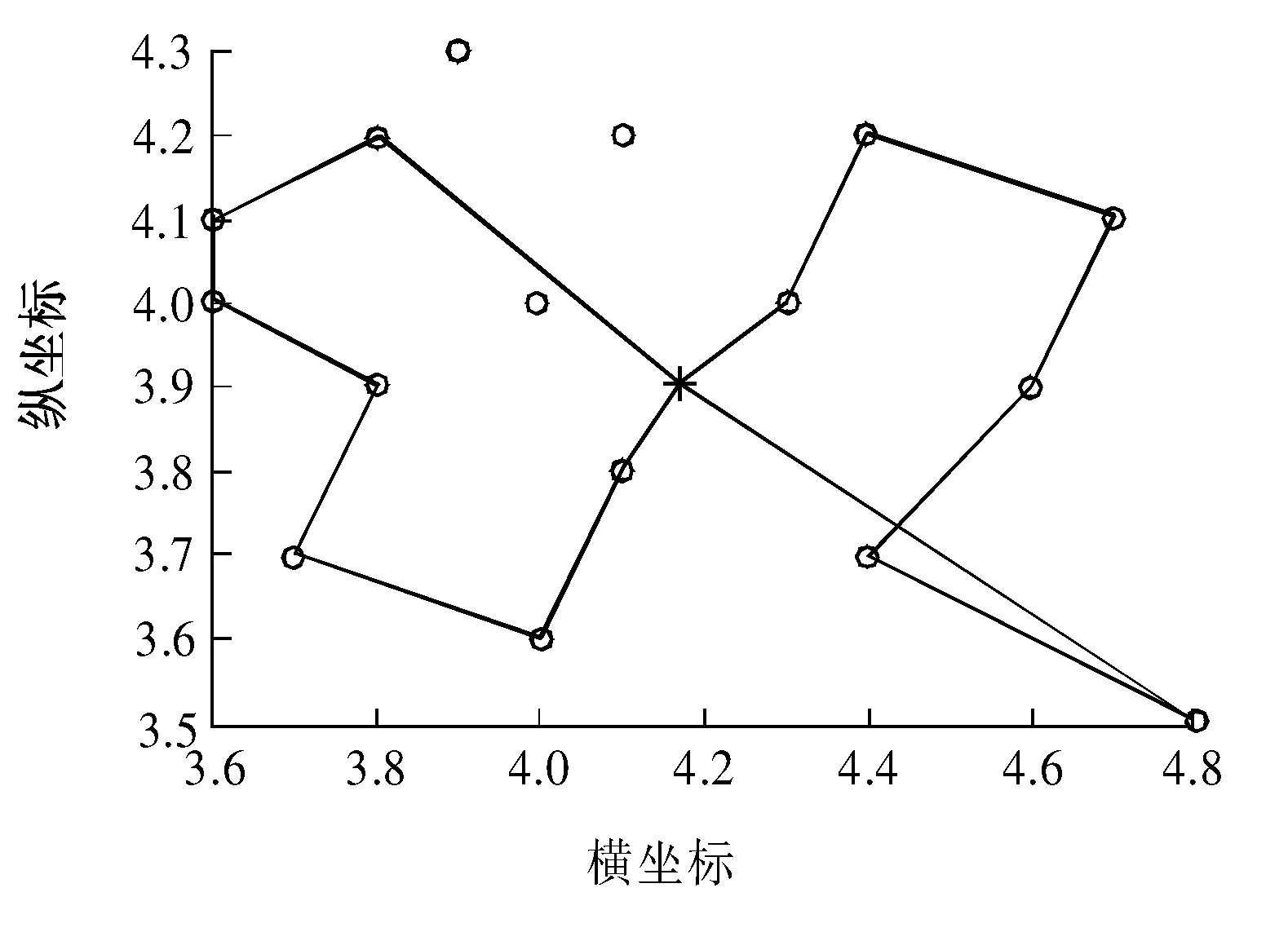
图6 运行路线Fig. 6 Running road map
5 结论
本研究综合考虑了乘客出行位置和支付意愿,设计了一种用于计算乘客出行中心点和确认孤立点乘客的算法。根据乘客出行位置和支付意愿,初步确定乘客出行中心点;依据乘客与乘客出行中心的吸引力大小,确认孤立乘客;在剔除孤立乘客后,重新计算乘客出行中心点。实验结果表明:采用重心位置的乘客出行中心点算法,能为接驳公交带来更大的乘客支付意愿收益。不过,现阶段的乘客出行中心点算法还没有把乘客的出行时间窗考虑进来,这将是下一步研究的方向。

