基于改进UKF的无轴承异步电机无速度传感器控制

孙宇新，沈启康，叶海涵，朱熀秋



基于改进UKF的无轴承异步电机无速度传感器控制

孙宇新，沈启康，叶海涵，朱熀秋

（江苏大学电气信息工程学院，镇江 212013）

基于传统卡尔曼滤波器的转速估计方法依赖于系统的精确数学模型，但目前通用的无轴承异步电机的数学模型是一个近似模型，针对该问题该文提出一种以实际转速为基准的改进的无轴承异步电机转速估算方案：首先，用残差归一化处理自动更新渐消因子并将其引入增益矩阵，以减小系统模型偏差对估算精度的影响，增强滤波器的稳定性；其次，用遗传算法自动更新噪声矩阵，使其具备补偿作用，再次优化转速估算精度，最终将估算精度控制在5 r/min左右，干扰误差控制在10 r/min左右，可有效应对建模误差和参数扰动对转速估算的影响，具备较高的鲁棒性和估算精度。最后，用dSPACE试验平台证明了所提方案的正确性和可行性，该研究为无轴承异步电机无速度传感器控制提供参考。

电机；控制；自适应渐消无迹卡尔曼滤波算法；改进AFUKF；无轴承异步电机；无速度传感器控制算法

0 引 言

在普通异步电动机的定子槽中附加产生径向悬浮力的线圈，用两套线圈共同生成的转矩和径向力可实现无轴承异步电机（bearingless induction motor，BIM）的转子旋转和稳定悬浮[1-5]。但在电机的运行过程中，需要实时检测转子转速作为相位信号以完成电机的闭环控制。由于BIM在运行时转子处于自悬浮状态，在轴上安装传感器不仅增加了硬件成本，还会严重影响电机的运行性能。因此，无速度传感器控制成为了BIM研究中的一个重要课题[6-8]，无速度传感器控制即通过实时检测电机的电压和电流来估算电机的实际转速，再将估算的转速反馈到系统中完成闭环控制，从而避免使用转速传感器，改善电机的机械性能。

近年来，大量文献提出了滑模观测器法[9-10]、神经网络法[11]、磁链观测法[12-13]、模型参考自适应法[14-16]、高频信号注入法[17-18]、卡尔曼滤波法[19-20]等无速度传感控制方法。其中卡尔曼法不受电压直流偏移量的影响，可有效抑制噪声，估计精度高，估算范围广，在电机无速度传感器控制中得到了广泛应用。卡尔曼滤波法中最常用的是扩展卡尔曼滤波法（extended kalman filter）[21]，该方法通过泰勒级数展开方法将非线性的电机模型近似线性化，再用卡尔曼算法迭代计算电机转速。针对扩展卡尔曼线性化误差较大、滤波精度不高的问题，学者相继提出了无迹卡尔曼滤波（unscented kalman filter）[22]和粒子滤波（particle filter）[23]，通过无迹变换和计算概率密度来代替扩展卡尔曼滤波中的近似线性化，从而获得更高的精度。针对卡尔曼滤波中的复杂矩阵运算，学者提出了几种降阶的卡尔曼滤波法[24-25]，通过降低协方差矩阵的阶数从而简化迭代过程。卡尔曼滤波还可以用于电机的参数估计[26]，通过将容易变化的电机参数增广到系统模型中，增强了系统鲁棒性。

但这些已经在普通异步电机上得到良好应用的方法推广至BIM时却出现了不匹配的情况。BIM通过电磁转矩和悬浮力的解耦运算分别构造出悬浮力数学模型和旋转部分数学模型，其中旋转力部分通常采和普通异步电机相同的数学模型。但这样的数学模型的前提假设为三相定子绕组和转子绕组在空间对称分布，且电机的转矩绕组和悬浮控制绕组相绕组轴线方向重合。因此，通用BIM的旋转部分数学模型是一个近似模型。由于卡尔曼滤波法对系统模型和电机参数非常敏感，且上述的各种改进方法并没有针对模型的不确定性进行改进，所以系统建模误差对转速估计的精度会产生很大影响。

为了提高系统的鲁棒性和精确性，本文提出一种基于改进的自适应渐消无迹卡尔曼滤波算的转速辨识法。通过利用残差序列的协方差，自适应地改变渐消因子以调整测量值，有助于减小陈旧测量值和系统模型不确定性对估计精度的影响。同时，通过对残差归一化处理，达到平衡各残差间信息的效果，提高了信息提取的速度。此外将剩余的系统模型误差部分视为噪声，用遗传算法对噪声矩阵进行自适应调整，并利用卡尔曼滤波的噪声矩阵对模型进行补偿，再次优化系统的估算误差。试验结果验证了以上方法的正确性和有效性。

1 BIM基本原理与数学模型

BIM绕组结构如图1所示，转矩绕组和悬浮控制绕组叠绕在同一个定子槽内。转矩绕组为四极绕组，用来产生电机转矩，悬浮控制绕组为二极绕组用来控制转子的径向位置。转矩绕组和悬浮控制绕组每相串联的有效匝数分别为1和2。在悬浮控制绕组和转矩绕组中分别通入电流1和2，则分别产生四极磁链2和4。和代表互相垂直的转子位置控制坐标轴。在空载情况下，如转子需要沿正方向的径向力则向径向力控制绕组中通入如图1所示的电流1，气隙上侧4和2同向，气隙磁密增加，气隙下侧4和2反向,气隙磁密减少，从而产生沿正方向的径向力。在悬浮控制绕组中通入反相电流，可产生沿反方向的径向力。同理，沿轴方向的径向力可以通过在悬浮控制绕组中通入与1垂直的电流获得。

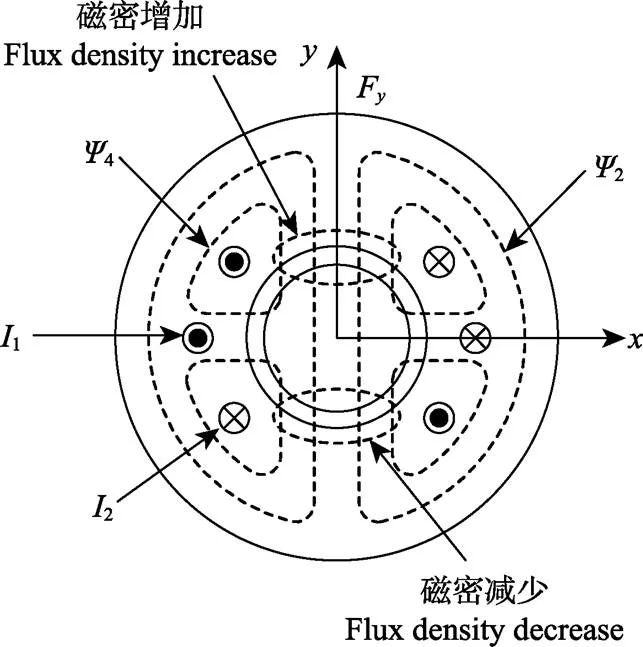
注：I1、I2分别为悬浮控制绕组和转矩绕组电流，A；Y2、Y4分别为两极磁链和四极磁链，Wb；Fy为y方向上的径向悬浮力，N。

BIM旋转部分采用转子磁场定向控制[27]。-坐标系下旋转部分的状态方程为：

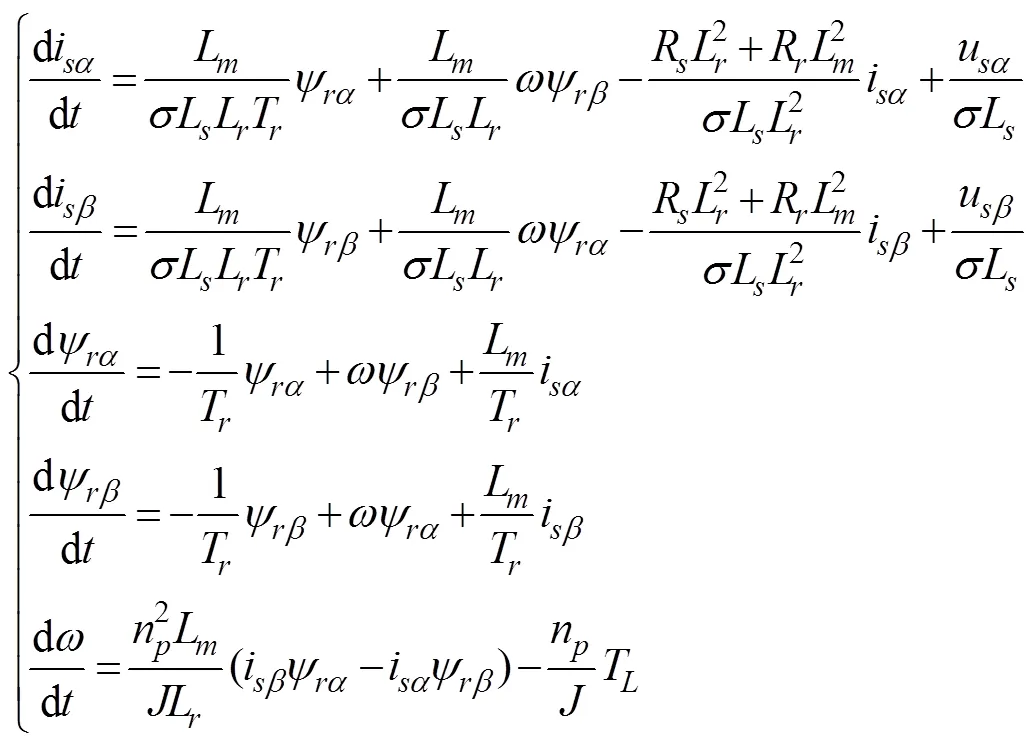
式中LLL分别为定子电感、转子电感和互感，R和R分别为定子电阻和转子电阻；为转动惯量；T为机械负载；n为电机极对数；为电机转子转速；为转子磁链；i为定子电流；u为定子电压，和为表示各参量在和轴上的分量；1-L2/LL为漏感系数；转矩T=L/R。

2 基于自适应渐消无迹卡尔曼滤波（AFUKF）算法的转速估计

2.1 AFUKF算法基本原理

已知维离散时间非线性系统：

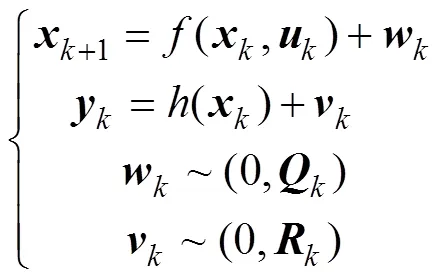
其中和分别表示在时刻的状态变量和测量向量；为时刻的输入量；是非线性状态方程函数；是非线性观测方程函数；和分别为过程噪声和测量噪声，它们是均值为零的高斯白噪声，设w具有协方差Q；v具有协方差R，则AFUKF算法的基本步骤如下：

1）滤波初始化

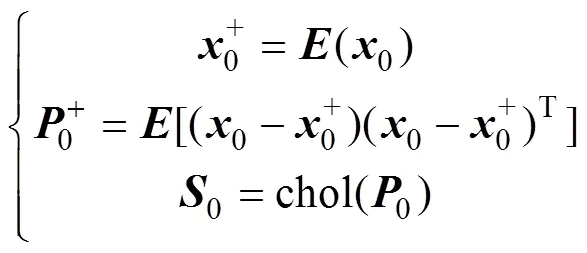
式中0+为误差协方差的初始矩阵，为单位矩阵。

2）时间更新方程

计算2+1个sigma点

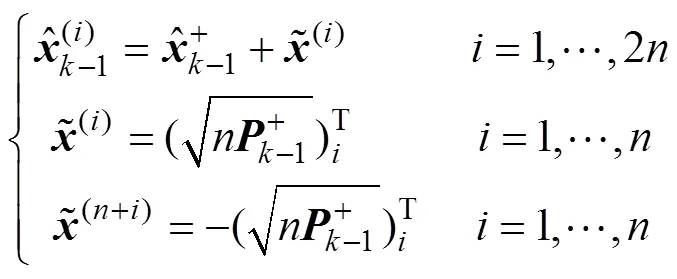
计算这些采样点的相应权值：

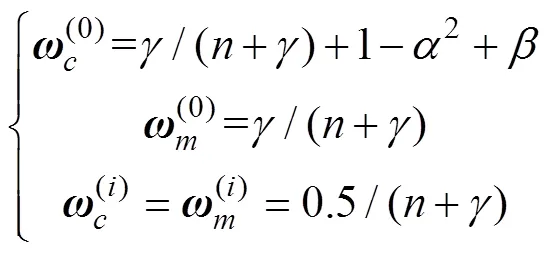
计算2+1个sigma点集的一步预测值：

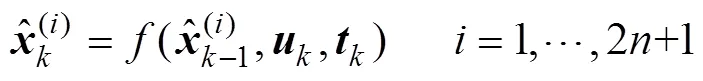
计算时刻的先验状态估计：

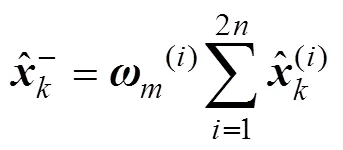
计算先验估计误差的协方差平方根阵－:

式中qr与cholupdate分别表示QR分解和Cholesky更新因子。

3）测量更新方程

根据一步预测值，再次使用无迹变换，得到新的sigma点集：

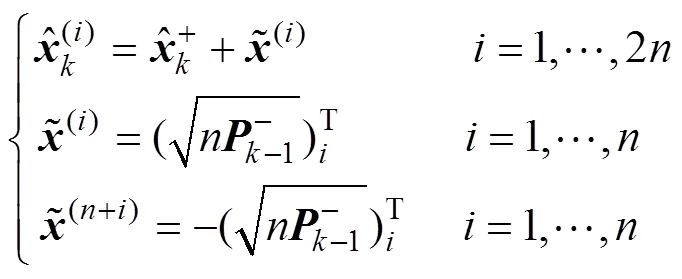
将点集带入观测方程：

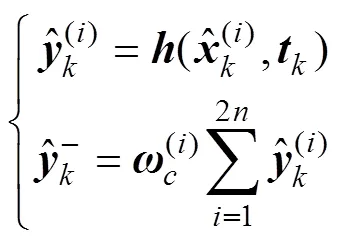
计算测量预测的协方差平方根和协方差阵：

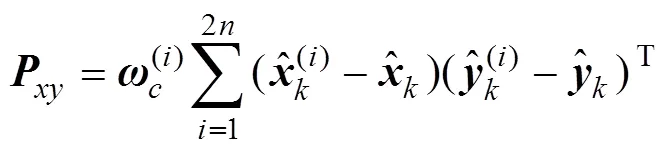
计算卡尔曼增益矩阵

计算系统的状态更新和协方差更新

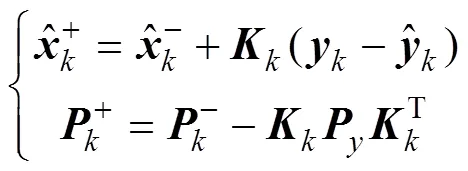
2.2 根据电机方程建立系统模型与观测模型

将式（1）中电机数学模型的状态方程离散化可得：

根据2.1中AFUKF算法基本原理异，选择A为非线性状态方程函数

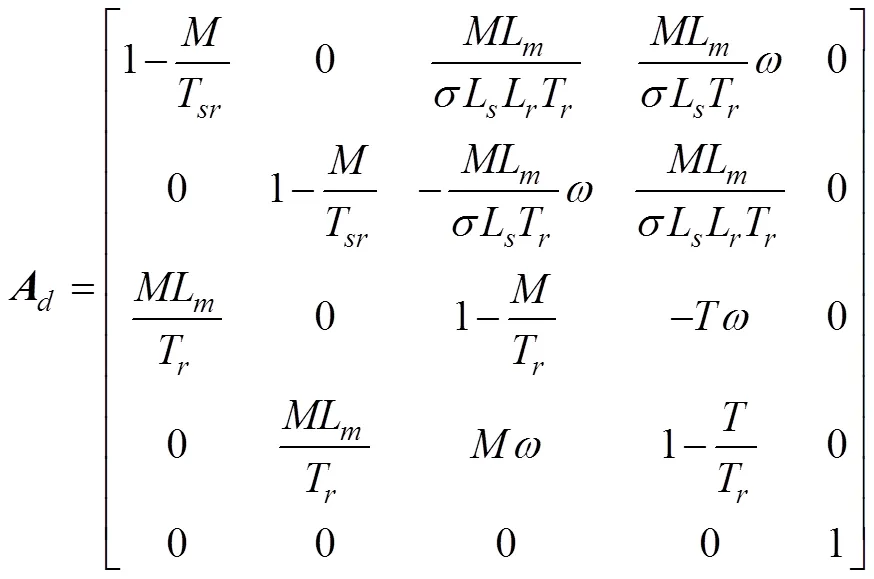
式中为采样时间，T=σL/R，R=R+(L/L)2。

根据该状态方程选取输出测量方程为：

2.3 AFUKF转速估计算法分析

由2.1节可见，自适应渐消无迹卡尔曼滤波在增益矩阵K中加入了渐消因子λ以区别于标准无迹卡尔曼滤波。当系统模型不准确时，实测量数对估计值的修正作用下降，而陈旧测量值的修正作用相对上升，这是引起系统发散的一个重要因素。为了减小模型误差对卡尔曼滤波的影响，在进行滤波时引入渐消因子使增益矩阵膨胀λ倍，加强现实测量数据在状态估计的作用，减小陈旧数据对系统的影响。其中，渐消因子的选择是AFUKF算法的关键。

在卡尔曼滤波中，时刻观测向量y的残差序列Z为：

其协方差阵为：

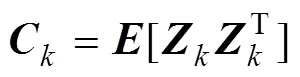
根据卡尔曼滤波的最优理论[27]，当增益阵为最优增益阵时新残差列应该处处保持正交[28]，即：

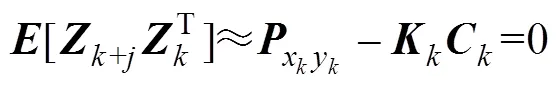
当系统模型不准确时，实际的残差协方差矩阵与计算出的理论值存在误差，残差的自相关函数不一定等于零。因此，本方案通过实时的调整增益阵K强迫残差序列保持相互正交，并通过该方法不断修正渐消因子。

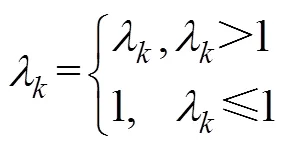
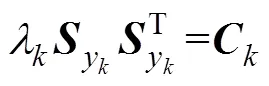
对上式求迹，得：

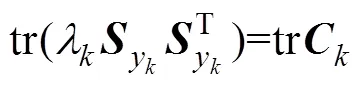
引入弱化因子可削弱λ的调节作用，避免过调节，使状态估计更平滑。

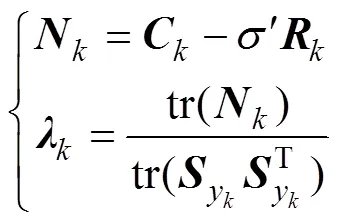
式中为遗忘因子，一般取值为0.95。

3 基于改进AFUKF的BIM无速度传感器控制算法 设计

上式中渐消因子的分子tr[]=tr[]-tr[βR]，且tr[βR]不受的影响。当≥1时：

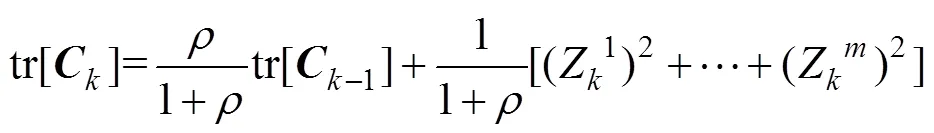
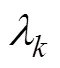
3.1 改进的AFUKF算法

针对AFUKF算法的不足，本文对残差计算进行改进。通过残差归一化处理，将算法中的和替换成¢和¢，优化渐消因子。引入对角矩阵=diag(1,2,…,η)，其中1,2,…,η≈1,2,…,y。为根据系统输出值大小的先验知识确定的比例关系，令：

则式（24）和（25）改写为

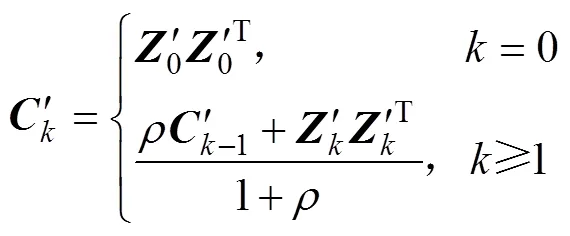
滤波残差的理论方差与实时辨识出方差应近似相互匹配，可得如下约束等式：

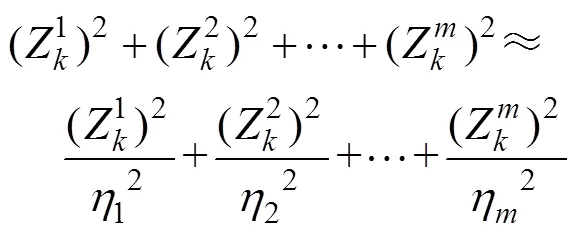
虽然Z无法预知，但能通过先验信息获得一组输出值01,02,…,0m来代替1,2,…,Z。可得方程：

归一化后各分量基本是相等，等式可化简为

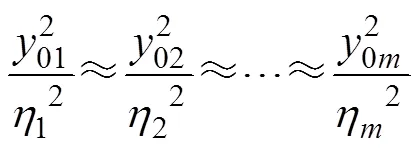
由上式可得：

上述算法通过残差归一化处理将原本算法中的和替换成¢和¢，有助于消除由残差本身数值差异造成的信息不对称，增加残差信息利用率和提取速度，有助于提高算法响应速度和暂态性能。

3.2 噪声矩阵优化

系统噪声通常来自系统模型误差和电压误差，而测量噪声包括检测电压、电流传感器干扰和A/D转换器量化误差等，并通过反复试凑寻找最合适的Q、R矩阵以实现最优滤波。当将其应用至BIM时，噪声还应包含模型误差，传统凑适法工作量加剧且精度不足，需要对系统进行精度补偿。因此，本文采用遗传算法优化噪声矩阵，补偿算法估算精度。

遗传算法[29]（genetic algorithm）是计算数学中用于处理最优化问题的搜索算法，它只需目标函数的值即可随机对代表参数的数字串全局寻优。因此，通过遗传算法可以将噪声矩阵的参数选择转化为多变量约束的最优化问题。根据BIM数学模型，构造系统噪声和测量噪声的协方差矩阵：

将待辨识矩阵中的7个正实元素组合成一个矢量：

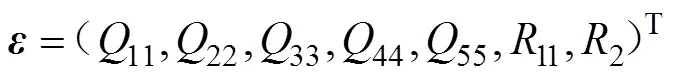
将各元素进行二进制编码得到子串，把个子串连成一个完整的染色体，记为一个个体。最初随机产生一定数目的个体组成种群作为初始群体，即随机产生个二进制串组成一个矢量

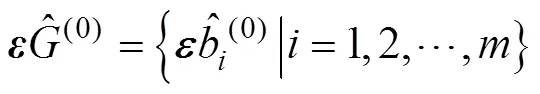
式中上标（0）代表第0代（初始代），上标^代表辨识值以区别于实测值。

每一个个体中元素的辨识值的限幅值约束为：

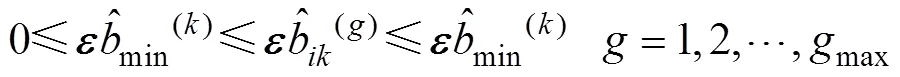
将测量方程输出的实际采样数据和滤波输出值的误差作为噪声矩阵的优化输入，以误差最小为优化目标。适应度目标函数如下:

式中为估计长度，通常取值范围为500～1500。

按适应度函数计算每个个体的适应度，用比例选择方式，将父代个体按适应度顺序排列，选取最前面ex个个体传递到子代中。将计误差超过预计值的个体丢弃，剩下的个体放入匹配池进行交叉变异，操作完成再把这些个体送回子代，形成+1子代群体后继续测试该群体的适应度。经过反复循环选择、交叉和变异的过程，可筛选出满足整个种群收敛条件的最优染色体，即可得到满足最优滤波条件的Q和R噪声矩阵。算法运行过程如图2流程图所示。

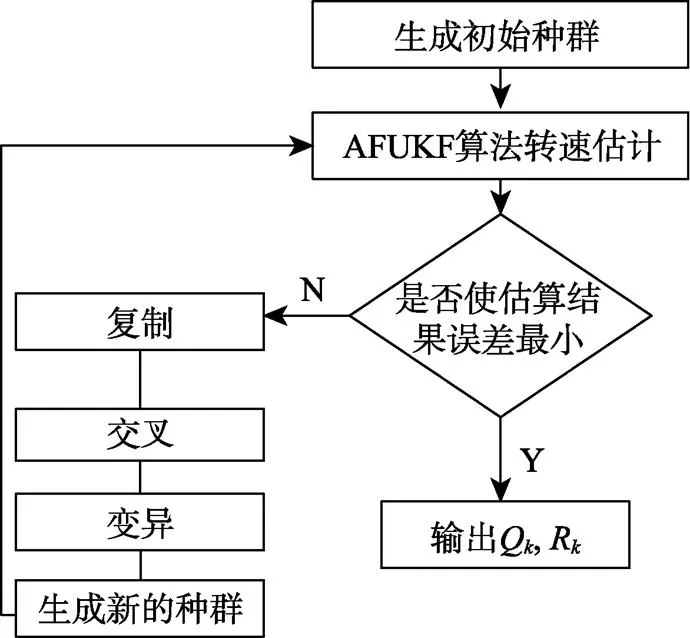
图2 噪声矩阵优化流程图

4 控制算法试验验证

将系统转态方程（15）和输出方程（17）带入式（2）‒（14）中就构成改进的AFUKF算法控制策略。图3为无轴承异步电机的控制框图，分为径向悬浮力控制部分和转矩控制部分，径向悬浮力控制是由位移传感器检测出的径向位移算出参考悬浮力，再生成悬浮控制绕组的电流信号来实现控制，通过对转子径向位移变化量进行检测，再通过位移调节器控制悬浮绕组中的电流来实现对径向位移精确控制。转矩控制部分采用气隙磁场定向控制，反馈转速通过改进的AFUKF算法模块计算。

本文的研究对象是一个复杂的时变系统，为了提高了试验的可靠性，本文选用由德国dSPACE公司开发的dSPACE1005作为核心控制器，依照图3的控制方案，设计了试验平台。图4所示为试验硬件平台，图5为组成框图。dSPACE1005的运算控制单元、CPLD最小系统模块、计算机、电流传感器、电压霍尔传感器、整流滤波模块、光电编码器和IPM(intelligent power module)及驱动模组成。其中定子电压、定子电流和转速分别由电流、电压霍尔和光电编码器测得，这些信号经信号调理板输入dSPACE1005，再由dSPACE1005完成改进的自适应渐消无迹卡尔曼滤波算法和噪声矩阵的遗传算法部分，最终将估算的实际转速反馈到系统中实现闭环控制，并将2种算法估算的转速通过示波器输出并对比，对于闭环控制系统，系统的故障监测和消除非常重要，因此需要设计对电压、电流的采样调理和保护电路，对于采样调理后的信号采用Lattice公司的CPLD（M4A5-96/48-10VC）进行逻辑处理和故障信号输出，dSPACE输出的PWM信号经过CPLD输出至芯片74F245中，以增强驱动能力，再输出至IPM中，最后通过IPM驱动电机。

注：x*、y*、x、 y分别为转子在x、 y方向上的给定位置和反馈位移，mm；Fx*、Fy*分别为径向悬浮力在x、y方向上的给定值，N；i*2sa、i*2sb为径向悬浮力绕组电流在a、b轴上的分量，A；i*2sd、i*2sq为径向悬浮力绕组电流在d、q轴上的分量，A；i*1sa、i*1sb为转矩绕组电流在a、b轴上的分量，A；i*1sd、i*1sq为转矩绕组电流在d、q轴上的分量，A；wr*为给定转速，r·s–1；wr为转子转速，r·s–1；ws为转子转差；Y1*为给定气隙磁链，Wb；Te*为给定转矩，N·m；q1*为电机旋转变换角，(°)；ρ0*为给定的补偿角，(°)；q2*为补偿后的电机旋转变换角，(°)；i*2A、i*2B、i*2C、i*1A、i*1B、i*1C分别为径向悬浮力绕组电流和转矩绕组电流的三相给定值，A；i2A、i2B、i2C、i1A、i1B、i1C分别为径向悬浮力绕组电流和转矩绕组电流的三相值, A；i1a、i1q为转矩绕组电流的估算值在d、q轴上的分量，A；u1a、u1q为转矩绕组电压的估算值在d、q轴上的分量, A。

试验中样机的参数为：转子漏感为L= 8.32 mH；定子漏感L= 5.75 mH；互感L= 64.5 mH；转子电阻R= 2.21 Ω；定子电阻R=1.36 Ω；转动惯量=0.0102 kg·m2。在遗传算法中取迭代次数为800；初始种群为70；选择操作比例因子为0.1；交叉概率=0.75；变异概率为=0.03。试验中以额定负载启动，给定转速为350 r/min。

图4 dSPACE试验平台

图6为电机的实测转速和改进的AFUKF算法估计的转速与普通的UKF算法估计的转速对比图，图7为改进的AFUKF算法估计误差与普通的UKF算法估计误差对比。从图中可以看出，普通的UKF算法受到电机模型精度的影响估计误差较大，为7.5 r/min左右，当将引入了渐消因子并用遗传算法优化噪声矩阵后估算精度得到改善，误差减小至5 r/min左右。

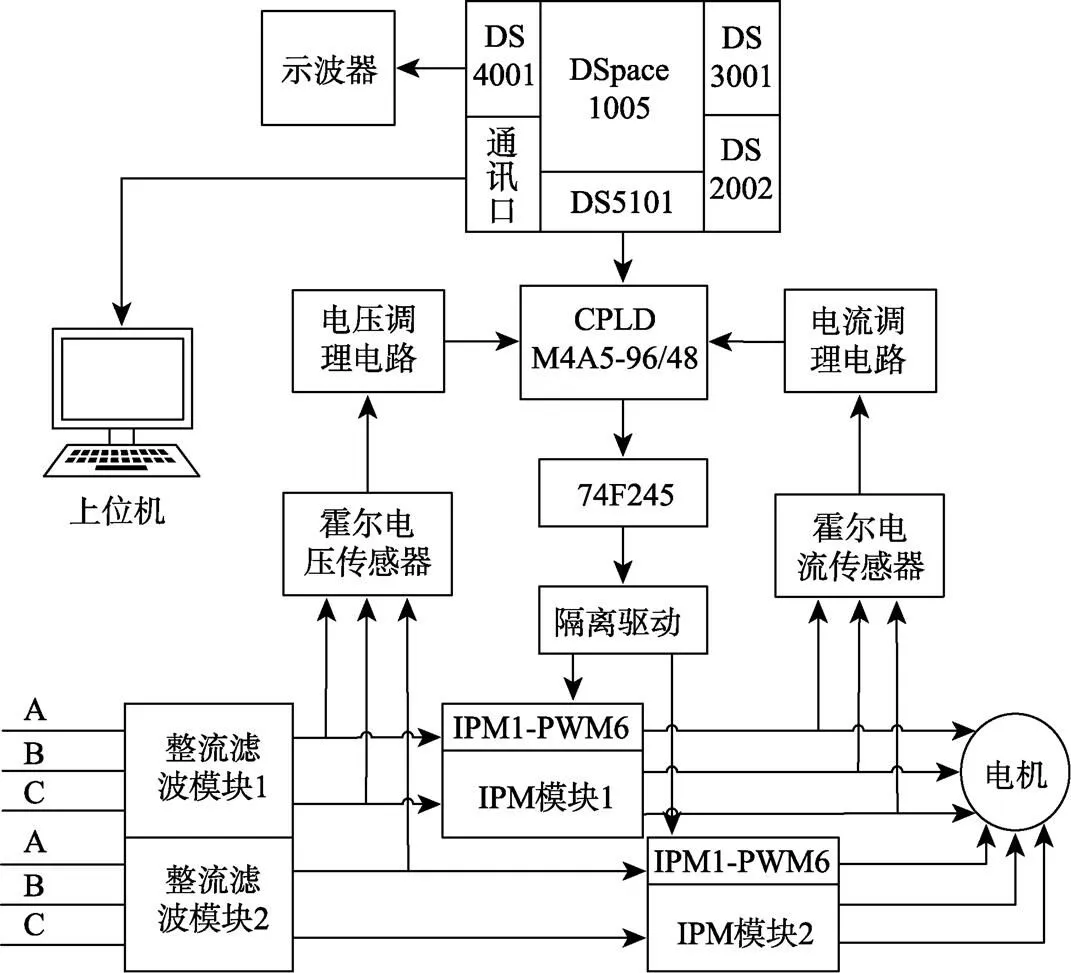
图5 试验平台控制框图

图6 改进AFUKF与UKF估计转速对比

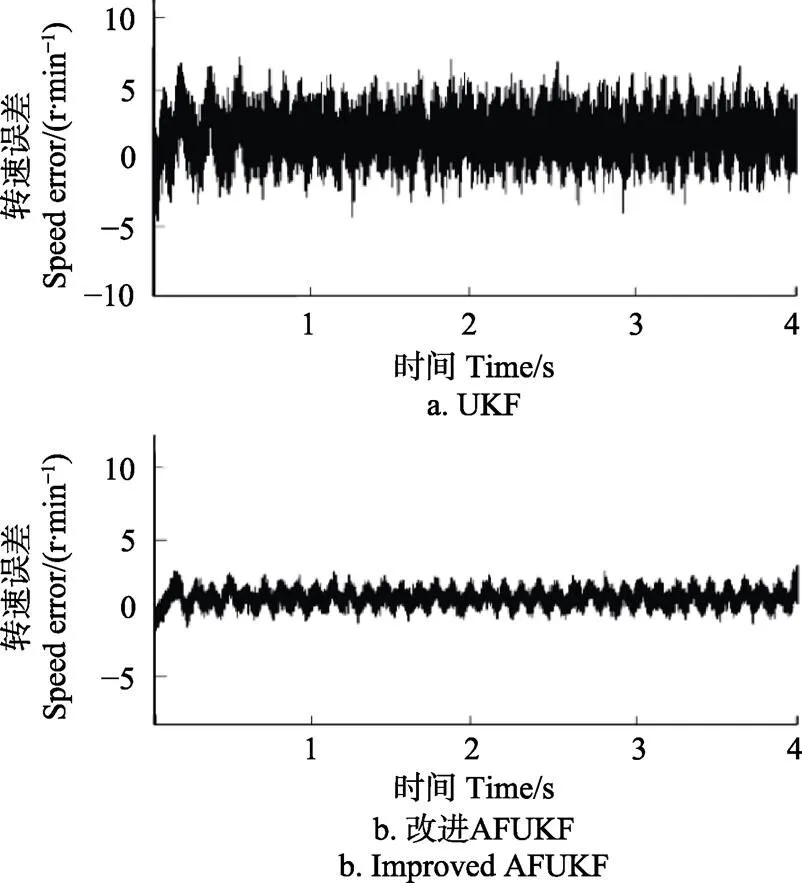
图7 改进AFUKF与UKF估计转速误差对比

为了验证算法的鲁棒特性，在1.2 s时刻对i施加一个幅值为1.5 A的脉冲干扰信号，改进的AFUKF算法和普通UKF算法的抗干扰误差对比如图8所示。可以看出在电流扰动时，AFUKF与UKF算法都存在波动，但普通UKF算法的估计误差最大值为20 r/min左右，改进的AFUKF算法的最大误差减小至10 r/min左右。

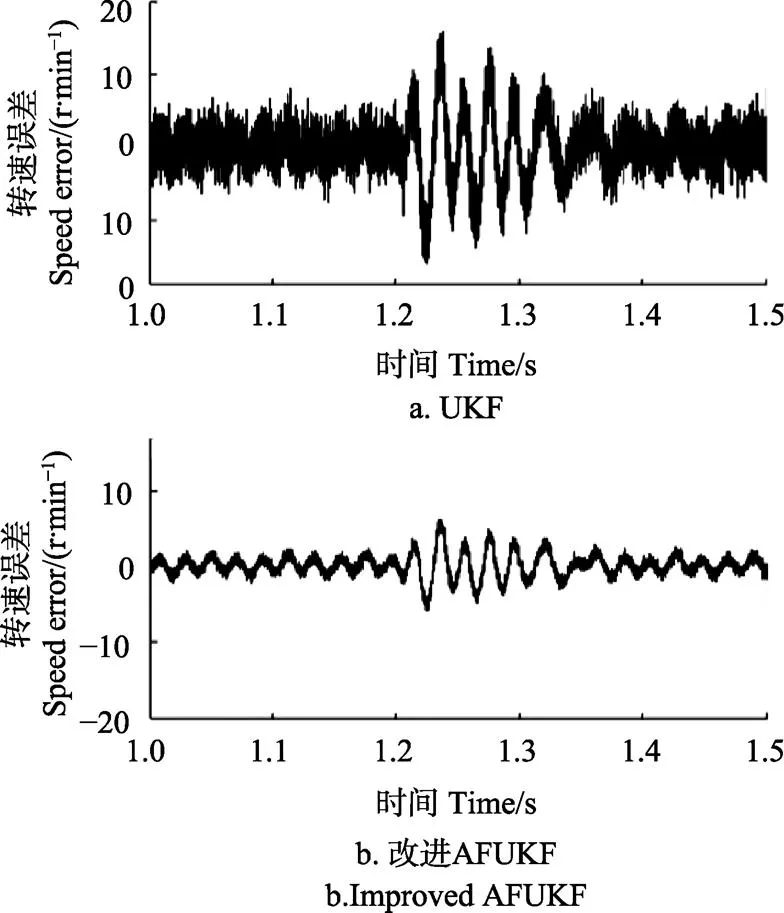
图8 改进AFUKF与UKF抗干扰误差对比

5 结 论

本文针对传统无轴承异步电机（bearingless induction motor，BIM）无速度传感器控制算法受制于电机模型精度的不足，提出了一种基于改进自适应渐消无迹卡尔曼滤波的BIM转速辨识方法，通过在系统中引入渐消因子增强了测量值在计算中的权重，减小了系统模型精度对估算精度的影响，并改进了渐消因子的计算方法，增强了残差的提取的速度使算法响应速度更快。同时采用遗传算法优化噪声矩阵。为了验证该方法的有效性，本文以dSPACE1005为核心对电机进行了实时控制，试验结果表明该方法能有效适应BIM模型不确定性，减小运行过程中转速估计的误差，将估算误差减小至5 r/min左右，并在外部干扰时有更强的鲁棒性，干扰误差减小至10 r/min左右。但该方法计算量较大，因此如何通过降阶的电机数学模型上实现该方法减小计算量将是下一步研究的问题。

[1] Li H, Zhu H. Design of bearingless flux-switching permanent-magnet motor[J]. IEEE Transactions on Applied Superconductivity, 2016, 26(4): 1－5.

[2] Jia H Y, Wang J A, Cheng M. Comparison study of electromagnetic performance of bearingless flux-switching permanent-magnet motors[J]. IEEE Transactions on Applied superconductivity, 2016, 26(4) : 1－5.

[3] Wu H, Wu H, Fang F, et al. Research on control strategy for a double-winding bearingless flux-switching machine with alternating excited orthogonal suspension windings[C]// Power Electronics and Motion Control Conference. IEEE, 2016: 821－826.

[4] 孙宇新，吴昊洋，施凯，等. 新型双绕组无轴承磁通切换永磁电机的设计与分析[J]. 排灌机械工程学报，2017，35(12)：1096－1104. Sun Yuxin, Wu Haoyang, Shi Kai, et al. Design and analysis of novel double-winding bearingless flux-switching permanent magnet machine[J]. Journal of Drainage and Irrigation Machinery Engineering (JD1ME), 2017, 35(12): 1096－1104. (in Chinese with English abstract)

[5] 卜文绍，万山明，黄声华，等. 无轴承电机的通用可控磁悬浮力解析模型[J]. 中国电机工程学报，2009，29(30)：84－89.Bu Wenshao, Wan Shanming, Huang Shenghua, et al. General analytical model about controllable magnetic suspension force of bearingless motor[J]. Proceedings of the CSEE, 2009, 29(30): 84－89. (in Chinese with English abstract)

[6] 戈素贞. 新型无轴承无刷直流电动机结构与模型研究[J]. 农业工程学报，2008，24(2)：131－135. Ge Suzhen. Configuration and model of innovative direct current motor without bearing and brush[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2008, 24(2): 131－135. (in Chinese with English abstract)

[7] 陈波，吴政球. 基于约束因子限幅控制的双馈感应发电机有功功率平滑控制[J]. 中国电机工程学报，2011，31(27)：131－137. Chen Bo, Wu Zhengqiu. Power smoothing control strategy of doubly-fed induction generator based on constraint factor extent-limit control[J]. Proceedings of the CSEE, 2011, 31(27): 131－137. (in Chinese with English abstract)

[8] 王晓琳，邓智泉. 无轴承异步电机磁场定向控制策略分析[J].中国电机工程学报，2007，27(27)：77－82.Wang Xiaolin, Deng Zhiquan. Analysis of flux-oriented strategies of bearingless asynchronous motor [J]. Proceedings of the CSEE, 2007, 27(27): 77－82. (in Chinese with English abstract)

[9] 程帅，姜海博，黄进，等. 基于滑模观测器的单绕组多相无轴承电机无位置传感器控制[J]. 电工技术学报，2012，31(23)：71－77. Cheng Shuai, Jiang Haibo, Huang Jin, et al. Position sensorless control based on sliding model observer for multiphase bearingless motor with singel set of windings[J]. Transactions of China Electrotechnical Society, 2012, 31(23): 71－77. (in Chinese with English abstract)

[10] 林茂，李颖晖，吴辰，等. 基于滑模模型参考自适应系统观测器的永磁同步电机预测控制[J].电工技术学报，2017，32(6)：156－163.Lin Mao, Li Yinghui, Wu Chen, et al. A model reference adaptive system based sliding mode observer for model predictive controlled permanent magnet synchronous motor drive[J]. Transactions of China Electrotechnical Society, 2017, 32(6): 156－163. (in Chinese with English abstract)

[11] 杨泽斌，汪明涛，孙晓东. 基于自适应模糊神经网络的无轴承异步电机控制[J]. 农业工程学报，2014，30(2)：78－86.Yang Zebin, Wang Mingtao, Sun Xiaodong. Control system of bearingless induction motors based on adaptiveneuro- fuzzy inference system[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2014, 30(2): 78－86. (in Chinese with English abstract)

[12] 陈振锋，钟彦儒，李洁，等. 基于改进磁链观测器的感应电机转速辨识[J]. 电工技术学报，2012，27(4)：42－47. Chen Zhenfeng, Zhong Yanru, Li Jie, et al. Speed identification for induction motor based on improved flux observer[J]. Transactions of China Electrotechnical Society, 2012, 27(4): 42－47. (in Chinese with English abstract)

[13] 韦文祥，刘国荣. 基于扩展状态观测器模型与定子电阻自适应的磁链观测器及其无速度传感器应用[J]. 中国电机工程学报，2015，35(23)：6194－6202. Wei Wenxiang, Liu Guorong. Sensorless control with flux observer based on parallel stator resistance adaptation and extended state observer model[J]. Proceedings of the CSEE 2015, 35(23): 6194－6202. (in Chinese with English abstract)

[14] 王庆龙，张兴，张崇巍. 永磁同步电机矢量控制双滑模模型参考自适应系统转速辨识[J]. 中国电机工程学报，2014，34(6)：897－902.Wang Qinglong, Zhang Xing, Zhang Chongwei. Double sliding-mode sodel reference adaptive system speed identification for vector control of permanent magnet synchronous motors [J]. Proceedings of the CSEE, 2014, 34(6): 897－902. (in Chinese with English abstract)

[15] 尹忠刚，刘静，钟彦，等. 基于双参数模型参考自适应的感应电机无速度传感器矢量控制低速性能[J]. 电工技术学报，2012，27(7)：124－130. Yin Zhonggang Liu Jing, Zhong Yan, et al. Low-speed performance for induction motor sensorless vector control based on two-parameter model reference adaptation[J]. Transactions of China Electrotechnical Society, 2012, 27(7): 124－130. (in Chinese with English abstract)

[16] Gadoue S M, Giaouris D, Finch J W. MRAS sensorless vector control of an induction motor using new sliding-mode and fuzzy-logic adaptation mechanisms[J]. IEEE Transactions on Energy Conversion, 2010, 25(2): 394－402.

[17] Chen Z, Gao J, Wang F, et al. Sensorless control for spmsm with concentrated windings using multisignal injection method[J]. IEEE Transactions on Industrial Electronics, 2014, 61(12): 6624－6634.

[18] 郑泽东，李永东，Maurice Fadel. 采用Kalma滤波器进行信号处理的高频信号注入法在电动机控制中的应用[J]. 电工技术学报，2010，25(2)：54－59，66.Zheng Zedong, Li Yongdong, Maurice fadel.application of high frequency signal injection method in motor control using kalman filter for signal processing[J]. Transactions of China Electrotechnical Society, 2010, 25(2): 54－59, 66. (in Chinese with English abstract)

[19] Alonge F, D'Ippolito F. Robustness analysis of an Extended Kalman Filter for sensorless control of induction motors [C]//IEEE International Symposium on Industrial Electronics. IEEE Xplore, 2010: 3257－3263.

[20] Yin Z G, Zhao C, Zhong Y R, et al. Research on robust performance of speed-sensorless vector control for the induction motor using an interfacing multiple-model extended kalman filter[J]. IEEE Transactions on Power Electronics, 2014, 29(6): 3011－3019.

[21] 张猛，肖曦，李永东. 基于扩展卡尔曼滤波器的永磁同步电机转速和磁链观测器[J]. 中国电机工程学报，2007，27(36)：36－40. Zhang Meng, Xiao Xi, Li Yongdong. Speed and flux linkage observer for permanent magnet synchronous motor based on EKF[J]. proceesings of the CSEE, 2007, 27(36): 36－40. (in Chinese with English abstract)

[22] Xu B, Zhu H, Ji W. State estimation of bearingless permanent magnet synchronous motor using improved UKF[J].Control Conference. IEEE, 2012: 4430－4433.

[23] Alrowaie F, Kwok K E, Gopaluni R B. An algorithm for fault detection in stochastic non-linear state-space models using particle filters[C]//International Symposium on Advanced Control of Industrial Processes. IEEE, 2011: 60－65.

[24] Quang N K, Hieu N T, Ha Q P. FPGA-based sensorless pmsm speed control using reduced-order extended kalman filters[J]. IEEE Transactions on Industrial Electronics, 2014, 61(12): 6574－6582.

[25] Smidl V, Peroutka Z. Advantages of square-root extended kalman filter for sensorless control of ac drives[J]. IEEE Transactions on Industrial Electronics, 2012, 59(11): 4189－4196.

[26] Barut M, Demir R, Zerdali E, et al. Real-time implementation of bi input-extended kalman filter-based estimator for speed-sensorless control of induction motors[J]. IEEE Transactions on Industrial Electronics, 2012, 59(11): 4197－4206.

[27] 孙宇新，杨玉伟. 无轴承异步电机非线性滤波器自适应逆解耦控制[J]. 农业工程学报，2016，32(14)：76－83.Sun Yuxin, Yang Yuwei. Adaptive inverse decoupling control for bearingless induction motors based on nonlinear filter[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2016, 32(14): 76－83. (in Chinese with English abstract)

[28] Dan S. Optimal state estimation: kalman, h∞, and nonlinear approaches[M].Optimal State Estimation: Kalman, H Infinity, and Nonlinear Approaches. Wiley-Interscience, 2006.

[29] 张勇军，王京，李华德. 基于遗传算法优化的定子磁链扩展卡尔曼估计方法[J]. 电工技术学报，2009，24(9)：64－70. Zhang Yongjun, Wang Jing, Li Huade. A method of the stator flux ekf estimation for induction motorsbasedon genetic algorithm optimizing[J].Transactions of China Electrotechnical Society, 2009, 24(9): 64－70. (in Chinese with English abstract)

Speed-sensorless control system of bearingless induction motor based on modified adaptive fading unscented kalman filter

Sun Yuxin, Shen Qikang, Ye Haihan, Zhu Huangqiu

(212013,)

Speed sensorless control estimates the speed of the motor by detecting the voltage and current in the motor, thereby avoiding the use of speed sensors in the system.This method can avoid the influence of the sensor on the rotation of the motor and effectively improve the speed regulation performance of the motor.The Kalman filter is widely used in speed estimation algorithm and this method is well applied to ordinary asynchronous motors, but when it is extended to bearingless induction motor(BIM), there is a mismatch, for the strong dependence of the Kalman filter on the system model, but the current mathematical model of the bearingless induction motor is an approximate model.Aiming at this problem, this study proposes a speed identification method based on improved adaptive fade-out unscented Kalman filter. By using the covariance of the residual sequence, to adaptively change the fading factor to adjust the weight of the new interest, so that the filtering algorithm is more convinced of the measured value in the estimation process, which helps to reduce the impact of stale measurement and system model uncertainty on estimation accuracy. At the same time, by normalizing the residuals, the effect of balancing the information between the residuals is achieved, and the speed of information extraction is improved. In addition, the residual part of the system model is regarded as noise. In order to further reduce the model error, the genetic algorithm is used to adaptively adjust the noise matrix. After repeated cycles of selection, crossover and mutation, the conditions for satisfying the whole population convergence can be selected. With the optimal chromosome, the noise matrixandof the Manchester filter satisfying the optimal filtering condition can be obtained, and the model is compensated by the matrix, and the estimation error of the system is optimized again. In order to verify the effectiveness of the algorithm, this study selects dSPACE1005 developed by German dSPACE company as the core controller and designs the experimental platform. The platform consists of the dSPACE1005’s arithmetic control unit, computer, current sensor, voltage Hall sensor, photoelectric encoder and IPM module. The platform consists of the dSPACE1005 arithmetic control unit, computer, current sensor, voltage Hall sensor, photoelectric encoder and IPM module. The stator voltage, stator current and rotational speed are measured by current, voltage Hall and photoelectric encoder respectively. These signals are input into dSPACE1005 through signal conditioning board, and then the improved adaptive fade-out unscented Kalman filter algorithm and noise matrix are completed by dSPACE1005. The effectiveness of the proposed method is verified by comparing the estimation results of Kalman filter and the improved adaptive AFUKF. The robustness of the proposed method is verified by comparing the anti-jamming capabilities of the two algorithms. Experimental results show that this control method has high robustness and precision, and can effectively deal with the influence of modeling error and parameter disturbance on the accuracy of speed estimation. Finally, the correctness and feasibility of the proposed scheme are proved by dSPACE experimental platform.

motors; control; adaptive fading unscented kalman filter; modified AFUKF; bearingless induction motor; speed sensorless control algorithm

10.11975/j.issn.1002-6819.2018.19.010

TP273

A

1002-6819(2018)-19-0074-08

2018-01-22

2018-06-14

国家自然科学基金项目（51675244）；江苏省重点研发计划项目（BE2016150）

孙宇新，教授，主要从事农业电气装备自动化、磁悬浮传动技术及电机非线性智能控制。Email：1000000656@ujs.edu.cn

孙宇新，沈启康，叶海涵，朱熀秋. 基于改进UKF的无轴承异步电机无速度传感器控制[J]. 农业工程学报，2018，34(19)：74－81. doi：10.11975/j.issn.1002-6819.2018.19.010 http://www.tcsae.org

Sun Yuxin, Shen Qikang, Ye Haihan, Zhu Huangqiu. Speed-sensorless control system of bearingless induction motor based on modified adaptive fading unscented kalman filter[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2018, 34(19): 74－81. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2018.19.010 http://www.tcsae.org