基于导抗变换器的ICPT恒流源补偿网络设计

朱 旺，周 知，王明锦，王 龙，于东升

（中国矿业大学信息与电气工程学院，徐州221116）

感应耦合电能传输技术ICPT（inductively coupled power transfer）实现了用电设备与电源之间非直接电气连接，避免了“有线”电能传输中存在的摩损、老化等问题，是一种安全、可靠、灵活的新型电能传输技术[1-5]，目前已经应用到矿井、水下等特殊场合。

在感应耦合电能传输系统中，能量经松耦合变压器从原边传递到副边，由于松耦合变压器耦合系数较低，所以系统能量传输效率不高，通常在原边与副边电路中增加补偿环节来实现谐振以提高系统传输性能[6-8]。基本补偿方式有串串（SS）、串并（SP）、并串（PS）和并并（PP）4 种，但是当负载动态变化时，简单的原副边串联或者并联补偿并不能同时实现系统的恒流输出以及单位功率因数输入特性，对于LED等需要恒流驱动的器件，无线电能传输系统具有较大的局限性。

为实现在动态负载模式下系统的恒流输出，文献[9]提出在逆变电路之前串入一个DC-DC环节，通过调节DC-DC的输出电压来控制输出电流恒定；文献[10]通过动态调节不同负载条件下原边注入能量实现输出电流控制；文献[9,11]通过检测原边电路电流，利用移相控制技术调节移相角的大小实现输出电流控制；文献[12]通过在原边加入LCL补偿拓扑实现原边电流恒定，在副边并联补偿的情况下实现恒流输出；文献[13,14]通过在原边加入LC元件，与松耦合变压器原边构成LCL补偿，通过电感的合理配置可以实现恒压或者恒流输出；文献[15]通过在原副边电路引入T型补偿网络实现恒流输出的负载无关性以及单位功率输入特性；文献[16]介绍了一系列高阶补偿拓扑，即原边或者副边使用串联或者并联补偿时，在另一边引入高阶补偿，使系统参数设计更为灵活；文献[17]提出一种双LCL谐振补偿方法，原边电流与输出电流在接收端与发射端相对位置确定时都可以保持不变。以上控制算法及补偿拓扑都可以实现输出电流的负载无关性，但是过多补偿元件的引入增加了电路体积，同时控制算法复杂，系统稳定性降低。

本文利用导抗变换原理，将松耦合变压器的原副边作为导抗变换器组成部分，通过参数的合理配置实现了输出电流的负载无关性以及单位功率输入特性，同时减小了电路体积。

1 基于导抗变换的补偿拓扑提出

1.1 RIC

导抗变换器IC（immittance converter）可以看成一个二端口网络，如图1所示，其中输入阻抗正比于负载导纳。导抗变换器在实现导纳-阻抗变换特性的同时，可以实现电压源与电流源之间的转换[12]。

图1 导抗变换器Fig.1 Immittance converter

IC输入输出之间满足的关系为

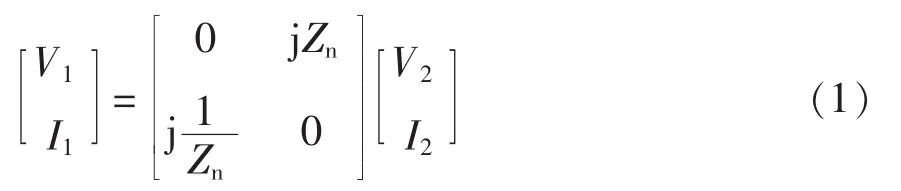
式中，Zn为电路的特性阻抗。

如果一个谐振变换器具有导抗变换特性，则可称之为RIC[18]，最常见的有T型与π型结构[18-20]，如图2所示。

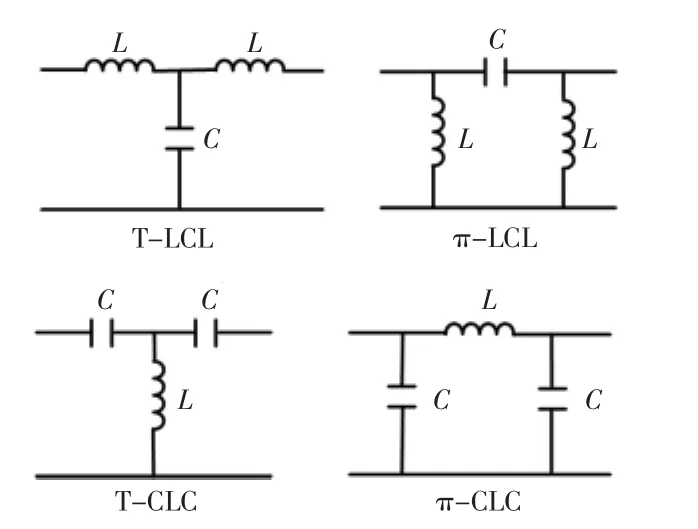
图2 典型导抗变换器拓扑Fig.2 Typical topologies of immittance converter

1.2 新型补偿拓扑

根据以上分析，如果将松耦合变压器的原副边电感作为RIC的组成部分，不仅可以实现输出电流的负载无关性，而且可以减少补偿元件数量，减小电路体积，降低设计成本。由文献[18]可知，图3（a）所示的基本导抗变换器拓扑结构可以同时实现导抗与谐振变换的功能。

在图3（a）中，当电容C由电感L与电容C1串联组成时，可以将L2、L3、L看作松耦合变压器的互感等效模型，而电容C1与电感L1看作补偿元件，其等效拓扑如图3（b）所示。基于导抗变换的ICPT恒流补偿拓扑如图4所示。

图3 4元件导抗变换器拓扑Fig.3 Topologies of immittance converter consisting of four elements

图4 基于导抗变换器的ICPT恒流补偿网络Fig.4 Constant-current compensation network for ICPT based on immittance converter

2 参数配置方法及系统特性

2.1 参数配置方法

忽略原副边线圈及补偿线圈内阻，在基波条件下图4电路等效为如图5所示。由于系统中存在较多储能元件，建模分析比较复杂，为简化电路分析过程，引入二端口网络。其中，Uin、Iin分别表示逆变输出电压与输出电流的基波分量，Uo、Io为导抗变换器即系统的输出电压、电流。由基尔霍夫定律可得

因此，等效电路的二端口的矩阵表达形式为

由以上分析可知，若此二端口可以实现导纳-阻抗转换，需满足 Z11=Z22=0，|Z12|=1/|Z21|，即

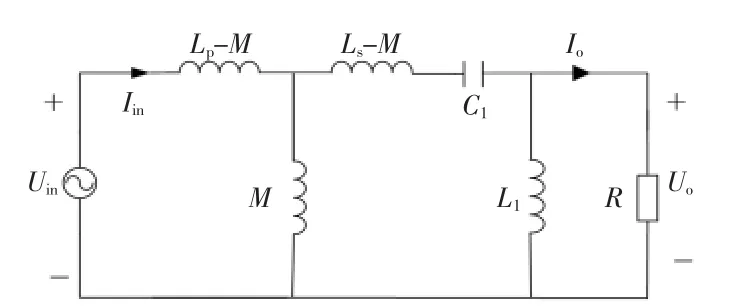
图5 导抗变换器补偿网络等效电路Fig.5 Equivalent circuit of compensation network based on immittance converter

式（5）表明，在其他系统参数不变的情况下，系统输出电流只与输入电压有关，而与负载无关。

对于图5所示电路，当电感Ls-M与电容C1等效为电容C时，系统输入阻抗为

由式（4）、式（6）可知，当系统满足式（5）且输入阻抗Zin为实数时，需满足

因此，系统参数配置方法可以遵循以下步骤：

步骤1根据系统需要，确定工作频率，也即谐振变换器的谐振频率。

步骤2当电感Ls-M与电容C1等效为电容C时，互感M与电容C需满足谐振要求，根据谐振频率，选择合适的互感M和电容C，然后再确定电感Ls与电容 C1。

步骤3确定互感M之后，根据式（8）选择合适的电感Lp与L1。

2.2 电路特性分析

根据配置系统参数的3个步骤，可以实现系统输出电流的负载无关性，且输入功率因数为1。为使结果更为直观，按照上述方法配置的系统参数如下 ：f=20 kHz，M=97 μH，Lp=194 μH，Ls=194 μH，C1=0.326 μF，L1=48.5 μH。

将上述参数代入式（5）和式（3），可以推导出系统电流增益以及逆变输出电流在归一化处理下的表达式，即

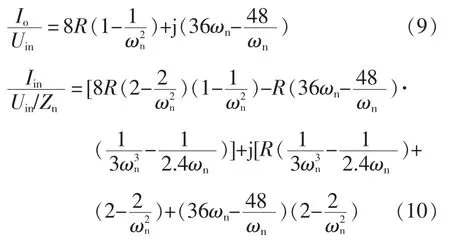
式中，Zn为导抗变换器的特性阻抗，Zn=ωoM。

图6和图7给出系统在不同负载时电流增益以及输入电流相角随工作频率变化关系。图中，横轴为归一化角频率 ωn，ωn=ω/ωo，ωo为系统谐振工作频率。可以看出，当系统工作在谐振频率时，在不同负载的情况下，输出电流与输入电压之比不变，亦即输出电流与负载无关；同样，在系统谐振频率处，对于不同的负载电阻，输入电流相角都为0，系统处于完全谐振状态，实现了系统单位功率输入。

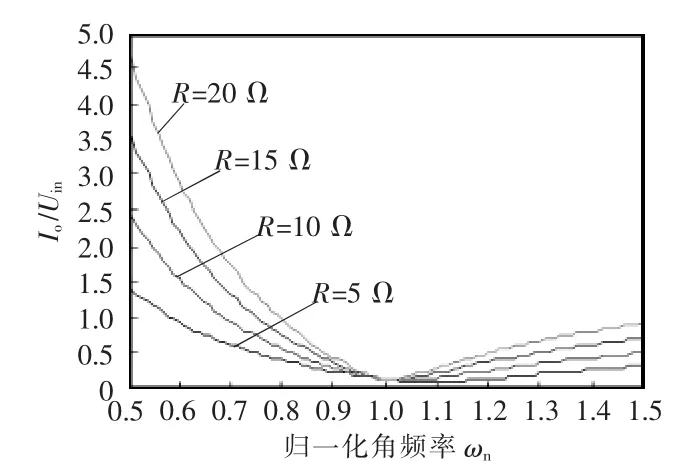
图6 不同负载下电流增益Fig.6 Current gain under different loads

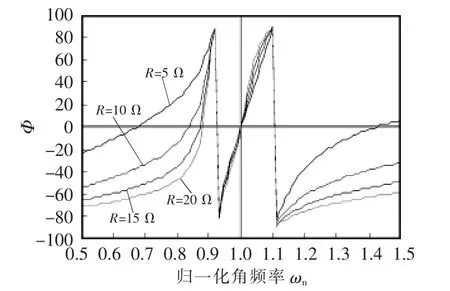
图7 不同负载下逆变输出电流相角Fig.7 Phase angles of output current from the inverter under different loads

为进一步分析本文电路的参数配置方式，对其传输效率进行推导。考虑到线圈原副边内阻及补偿电感内阻，系统实际的等效电路模型如图8所示。谐振状态下系统输出功率Pout及电路损耗功率Ploss可以表示为

式中，Is和IL1为流过副边电感和补偿电感的电流。则有

因此，系统的传输效率η可表示为

根据式（13），系统传输效率曲线如图9所示。可见，随着负载的增加，传输效率下降，即系统在低功率时具有较高效率。

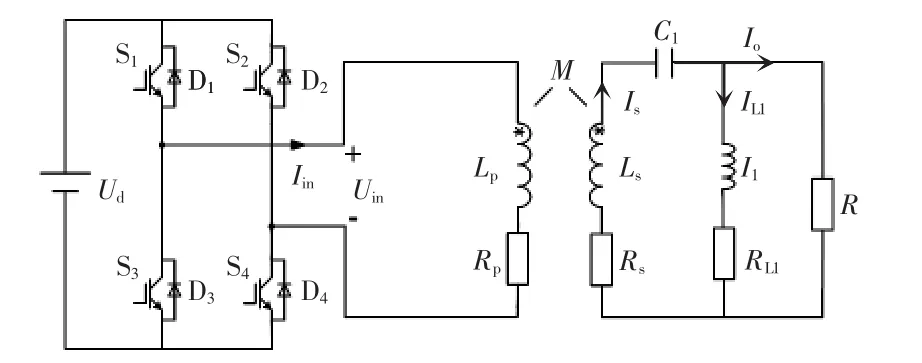
图8 系统实际等效电路模型Fig.8 Equivalent circuit model of the practical system

图9 效率η与负载R的关系Fig.9 Relationship between efficiency η and load resistor R

3 系统参数优化

记通过电感Lp-M、互感M、电容C和电感L1的电流分别为 Iin、Im、Ic和 IL1，而 ZLs-m、Zc、Zm和 ZL1为各元件阻抗，由图5可知

通常情况下，在谐振槽中，相较于电容元件，电感更大且更重。电感的物理尺寸可以由面积乘积表示，并且正比于电感储存释放的能量，可以根据文献[21]推导归一化的电感总能量，表示为

谐振回路的电抗元件增加了系统的体积，因此必须对参数进行优化。通常将谐振网络的视在功率与有功功率之比作为衡量系统体积的指标[12，21-22]，比值越小，系统体积越小。定义视在功率与有功功率比值为λ，即

将式（14）～式（19）代入式（21）可得

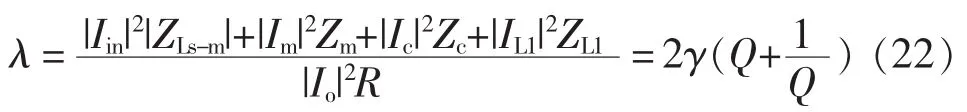
根据式（20）、式（22）可得 S/P 与 En随Q 值变化的曲线，如图10所示。从图中可以看出，存在一个Q值使S/P最小，并且随着Q值的增大，En值一直减小，因此，该Q值可以起到减小系统体积的作用。当且仅当Q为1时，λ最小，且λ=4γ。然后，在工作频率与负载确定情况下，可以确定电感L1的取值，最后根据第2.1节所述的参数配置方法选择其余参数。

图10 S/P与En随Q值变化曲线Fig.10 Curves of S/P and Enversus variable Q

4 仿真分析

为了验证本文理论分析的正确性以及参数配置的合理性，根据系统参数优化原则以及配置方法，应用Matlab/Simulink系统仿真软件进行仿真分析。系统中各元件参数见表1，仿真结果见图11。

在启动后1 s时，负载由5 Ω突变为10 Ω时，系统输出电流io的波形如图11（a）所示。由图可知，当负载发生突变时，系统输出电流幅值仅发生了十分微小的变化（约为0.001 A），即系统具有很好的恒流输出特性。

逆变器输出电压uin和电流iin波形分别如图11（b）和（c）所示，可以看出，在负载发生变化前后，uin和iin基本保持同相，即实现了单位功率因数输入特性，且可保证系统始终工作在谐振频率处，具有较好的系统稳频特性。

表1 ICPT系统仿真参数Tab.1 Simulation parameters of ICPT system

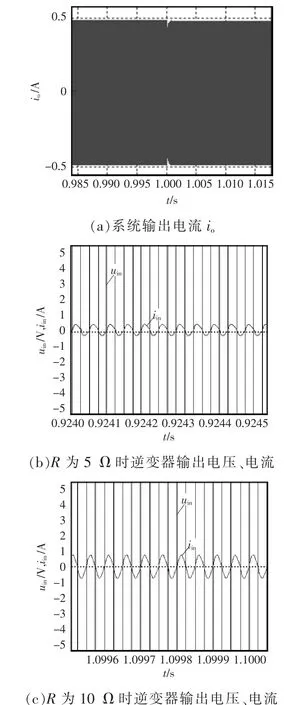
图11 仿真结果Fig.11 Simulation results

5 实验结果与分析

根据表1实验参数及图4搭建实验平台，实验结果如图12所示。在实验过程中，逆变输出电流iin以及系统输出电流io采用霍尔电流传感器转变成数值相等的电压值。

由图12（a）可知，在负载发生变化时，系统输出电流略微减少，这主要是由于实验中元器件参数误差引起的，如原副边线圈以及补偿电感内阻等。图12（b）和（c）给出了负载电阻分别为 5 Ω、10 Ω 时逆变器输出电压、电流波形。由图可知，电压电流基本同相，验证了系统处于完全谐振状态，即系统单位功率因数输入特性，表明此ICPT系统可降低器件功率容量要求，减少器件的电压应力，降低系统设计成本。

图13给出了系统在不同负载下的传输效率，与图9基本一致，传输效率有所下降，这主要是由开关管损耗以及线圈内阻引起，该补偿拓扑在低负载时可以获得较大效率。

图12 实验结果Fig.12 Experiment results

图13 不同负载时系统效率Fig.13 System efficiency under different loads

6 结语

本文利用导抗变换思想将松耦合变压器以及补偿元件等效为导抗变换器，以减少补偿元器件的数量、减小电路体积，实现系统输出电流的负载无关性。另外，系统实现了单位功率因数输入特性。文中给出了系统参数配置方法，在减小系统电路体积的前提下对系统参数进行了优化。仿真与实验结果验证了理论分析的正确性，此ICPT电路可应用于LED等需要恒流供电的场合。